复4D超混沌系统的镇定与同步问题

张文珠,王佐勋,潘锦浩,宋 聪

齐鲁工业大学(山东省科学院)信息与自动化学院,山东 济南 250353

自1963年Lorenz首次发现混沌系统以来,具有重要研究价值的热门方向是混沌系统及其现象[1]。状态变量属于复空间的复混沌系统是另一种重要的混沌动力系统[2-3]。它在定理和应用上得到了广泛的研究,成为近年来的热门话题之一。特别是由于复混沌系统是由实数和虚数组成的,它比实混沌系统具有更好的加密效果[4-5]。由于复混沌系统的动力学行为比实混沌系统更为复杂,因此研究此类系统的控制问题非常困难。

传统的线性反馈控制器虽然结构简单,物理上易于实现,但也存在过分依赖控制反馈增益值的问题,极大地限制了系统初始值设定的自由度[6-8]。目前,大多数研究人员采用以下方法：首先,通过分离复状态变量的实部和虚部,将复混沌系统转化为其等价的实混沌系统,然后为被控制的实混沌系统设计相应的控制器,最后根据复混沌与其等价实混沌系统之间的对应关系,得到复混沌系统的对应控制器,从而实现对这类复混沌系统的控制问题[9-10]。但是,这种方法也存在一些问题：一方面,第一步缺乏系统的方法,即对于特定的复混沌系统,如何找到系统的方法将复混沌系统转化为与其等价的实混沌系统,不仅具有重要的理论意义,而且具有广泛的应用价值[11-12]；另一方面,前人设计的控制器大多是复杂[13-15]；因此,它们很难在实际情况中应用[16-18]。关于求解非线性系统的控制问题,物理学上也有控制器可供选择,动态增益反馈控制器为就是其中之一[19]。

本文的主要贡献是利用动态反馈控制方法为复4D超混沌系统设计了几个物理控制器。与以往的研究成果相比,这种控制器将更为简单,并可以实现复4D超混沌系统的稳定和完全同步。最后通过Matlab进行数值模拟,模拟结果验证了理论结果的正确性和有效性。

1 理论准备

考虑如下混沌系统：

其中,x∈n是系统的状态变量,f(x)=(f1(x),f2(x),…,fn(x))T是连续光滑的向量函数并且f(0)=0。

设系统(1)为主系统,则相应的受控从系统为：

其中,y∈n是系统的状态变量,f(y)=(f1(y),f2(y),…,fn(y))T是连续光滑的向量函数,B∈n×r是常数矩阵且r≥1,u是待设计的控制器。

令e=y-x,则可以得到误差系统如下所示：

其中,e∈n是系统的状态变量,B和u已经在(2)中给出。

2 问题描述

一个复4D超混沌系统,系统中的每个方程都有一个三项叉积,表示为

令m=x1+ix2,n=x3+ix4,p=x5,q=x6,则系统(4)可以转化为以下等价的实系统

其中,x∈6是系统的状态变量。

设系统(5)为主系统,则相应的受控从系统为：

其中,y∈6是系统的状态变量,u是待设计的控制器,B被设计为

3 主要结果

在本节中,我们通过动态反馈增益的方法来实现复4D超混沌系统的镇定和同步问题。

定理3.1 考虑系统(6),如果被设计的控制器u是

u=k1(t)BTy,

(7)

其中

说明系统(6)实现了镇定。

证明：令x3=x4=x5=0,则相应的三维子系统为

是渐进稳定的。因此,(f(y),B)是可控的,这就完成了证明。

定理3.2考虑主系统(5)和从系统(6),如果被设计的控制器u是

u=k1(t)BTe,

(10)

其中e=y-x,

说明主系统(5)和从系统(6)实现了完全同步。

证明：令e=y-x,则误差系统为

其中e∈6且

其中：

G5(x,e)=(y1y3y6-x1x3x6)+(y2y4y6-x2x4x6)-ce5,

(14)

G6(x,e)=(y1y3y5-x1x3x5)+(y2y4y5-x2x4x5)-de6,

(15)

显然,如果e3=e4=e5=0,且a=20,b=10,c=1,b=2,则相应的三维误差系统为

是渐进稳定的。因此,(G(x,e),B)是可控的,这就完成了证明。

4 数值仿真

受控复4D超混沌系统的初始值为x(0)=[1,1,2,2,3,3,-1],动态反馈增益k(t)的初始值k(0)=-1,仿真结果如下图所示。从图1和图2中可以看出复4D超混沌系统的每个状态变量是渐进稳定的,图3表明动态反馈增益k(t)收敛到一个合适的常数。

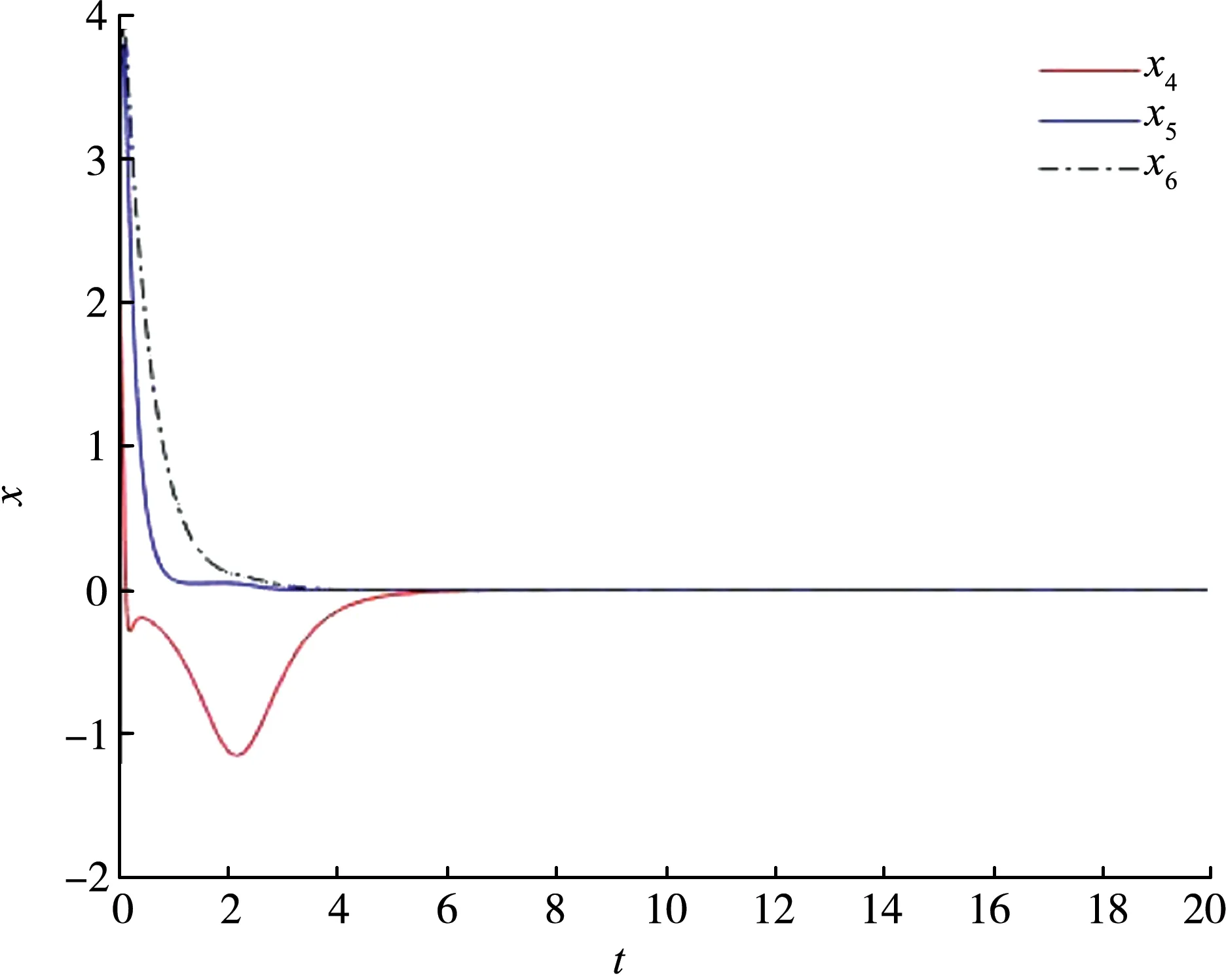
图2 状态变量x4、x5、x6渐进稳定

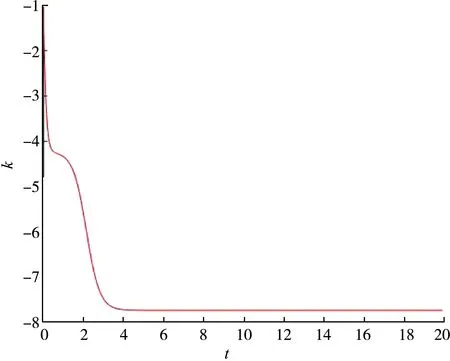
图3 动态反馈增益收敛到一个合适的常数

主系统的初始值x(0)=[-1,-2,3,2,-1,2],从系统的初始值y(0)=[3,2,-1,-2,3,-2],动态增益反馈k(t)的初始值k(0)=-1。仿真结果如下图所示。从图4和图5中可以看出控制器被激活时的误差系统,表明已经稳定,这意味着复4D超混沌系统中完全同步已经实现。图6和图7显示了控制器启动时状态变量的动态变化,主系统和从系统的状态实现了完全同步,图8表明动态反馈增益k(t)收敛到一个负常数。

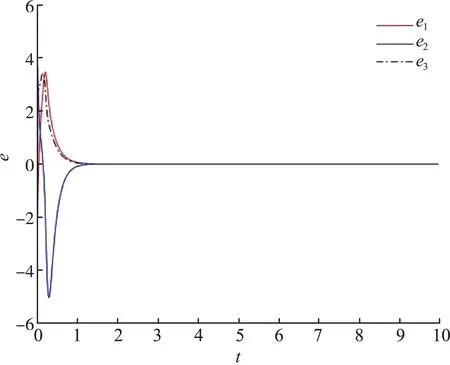
图4 误差系统e1、e2、e3渐进稳定

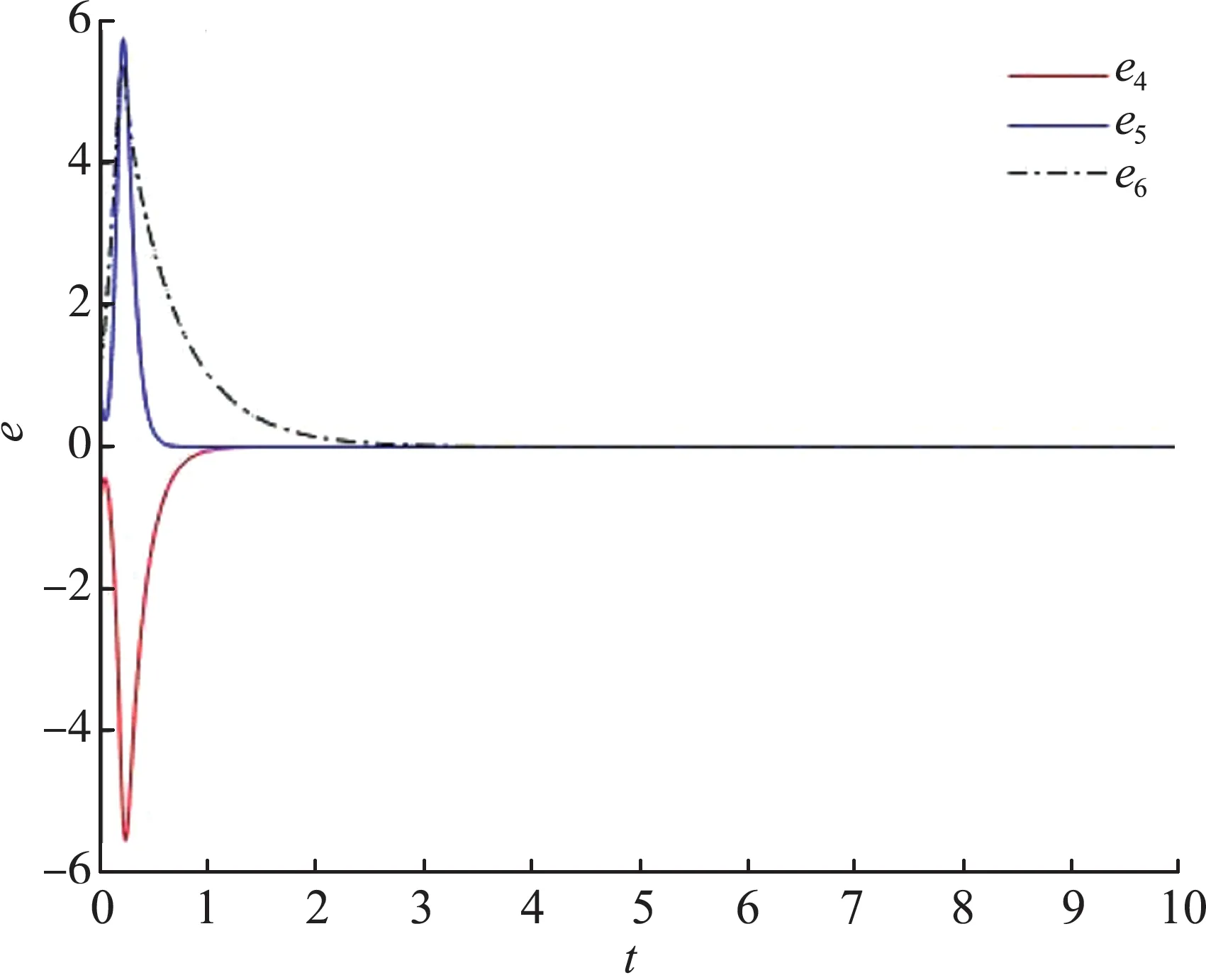
图5 误差系统e4、e5、e6渐进稳定

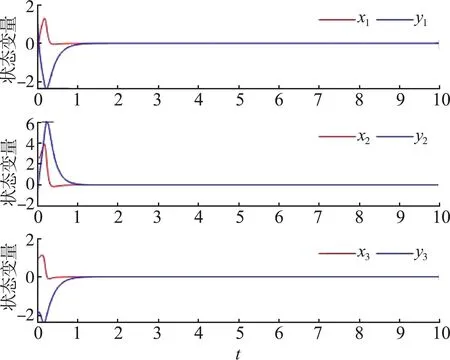
图6 主系统x1、x2、x3和从系统y1、y2、y3的状态实现了完全同步

图7 主系统x4、x5、x6和从系统y4、y5、y6的状态实现了完全同步

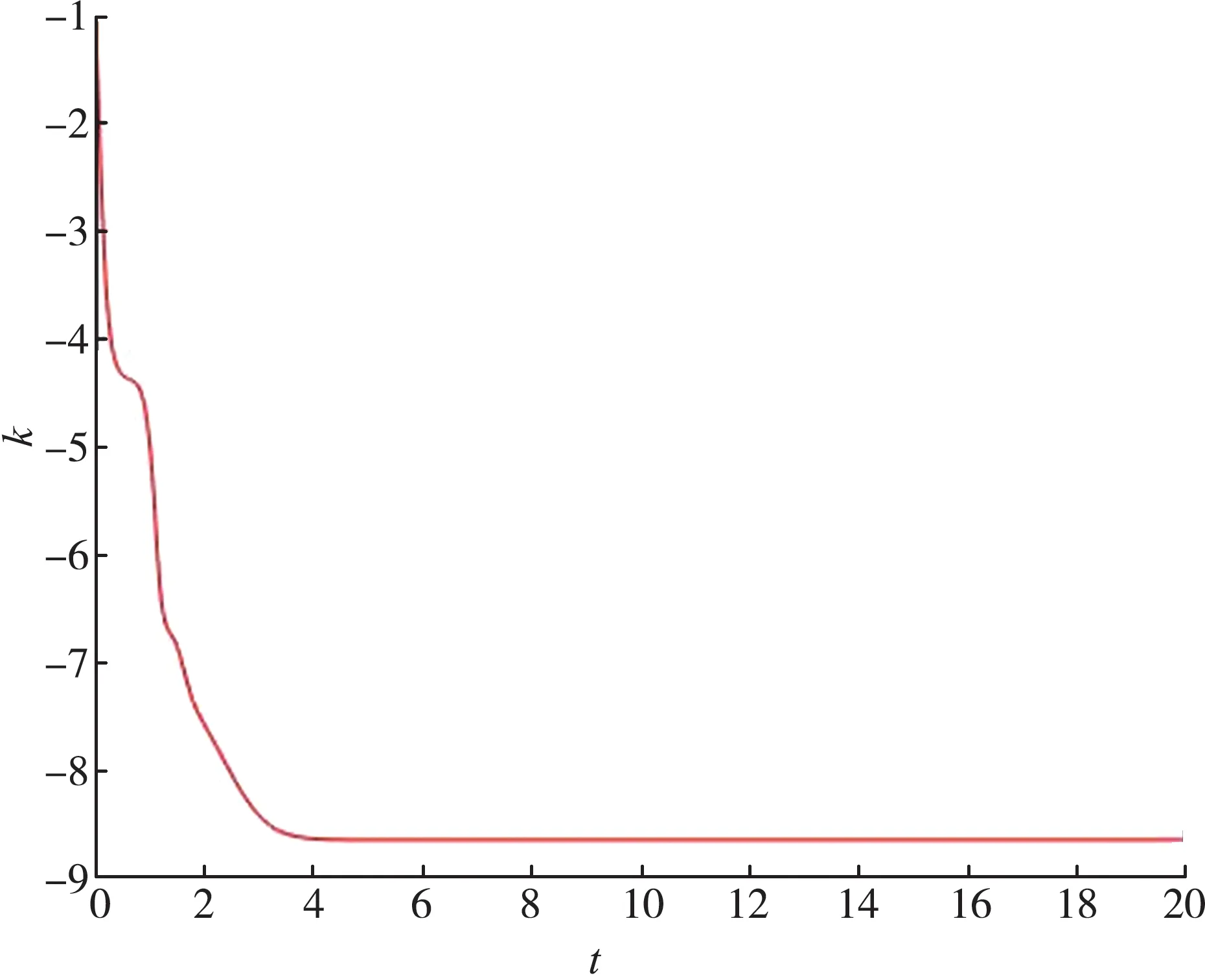
图8 动态反馈增益收敛到一个合适的负常数

5 结 论

本文研究了通过动态增益反馈控制的方法来实现复4D超混沌系统的镇定和同步问题。首先,通过分离复变量的实部和虚部,将复4D超混沌系统转化为等价的六维实系统。然后,设计两个简单的控制器来实现复4D超混沌系统的镇定和同步问题。最后,通过Matlab进行数值仿真验证了理论结果的正确性和有效性。本文提出的研究方法也可以应用于其他混沌或超混沌系统。