基于AFSA-RF的两相流型图扩展技术

李旭鹏，钟文义，乔守旭,*，谭思超，王庶光

(1.哈尔滨工程大学 黑龙江省核动力装置性能与设备重点实验室，黑龙江 哈尔滨 150001；2.哈尔滨工程大学 核安全与先进核能技术工信部重点实验室，黑龙江 哈尔滨 150001)

气液两相流的流型是化工、石油以及火力、核能发电等行业生产过程中的一个重要参数[1-2]，对流型的精准预测对于生产应用有着重要意义。当今的流型识别，主要依靠可视化技术得到的图像和电导探针、电阻式空隙仪所得到的水力特性来进行研究[3-5]。这些实验研究对于两相流特性有较好引导作用，但此类流型识别的方法主要以可视化方法为主，具有一定主观性。实验中所得到的两相流型图为经验流型图[6]，其水和空气的表观流速均处于低流速区(0～4 m/s)，无法满足实际生产应用。

为解决上述流型识别研究中的问题，随着近年来机器学习的快速发展，诸多国内外学者建立了基于人工神经网络的两相流流型软测量模型，并取得了较好效果[7-10]。但神经网络模型有以下几个缺点[11]：1) 收敛速度慢，需要大量的时间成本与算力；2) 需要大量特征量来训练以防止过拟合，两相流的特征较为难取；3) 需要较庞大的训练集进行训练以保证预测精度，而大多数情况下仍以开展小批量实验为主，获得样本数据较少，使得其工程应用较为困难。对于少样本、少特征条件下分类，适用的模型组要有支持向量机(support vector machine, SVM)、K近邻算法(K-nearest neighbor, KNN)和决策树(decision tree, DT)3种。这3种模型的识别效果均优于人工神经网络，其中属SVM的预测精度最佳[12]。然而单一的简单分类器精度无法超越集成学习模型(ensemble learning, EM)[13]，其中以决策树为基分类器的随机森林(random forest, RF)算法可以满足精度要求。

RF是Bagging集成方法中最具有代表性的算法[14]，通过集成每棵树的分类结果进行投票最终得出分类结果。近十几年来，RF算法在各领域均得到了飞速发展，在生物学、信息技术、地理地质及经济管理等领域中均有广泛应用[15-19]。

人工鱼群算法(artificial fish swarms algorithm, AFSA)[20]是一种新型的优化算法，该算法利用了鱼的聚群、觅食和追尾这3个基本行为，采用自上而下的寻优模式从构造个体的底层行为开始，通过鱼群中各个体的局部寻优，达到全局最优值在群体中凸显出来的目的。

本文提出一种利用基于AFSA优化RF的优化识别模型，用以开展竖直下降两相流流型的精准预测。通过对流量计所获得的气液两相流速、雷诺数、施密特数以及处理后特征数进行训练，实现对实验较难达到的高流速区进行预测。

1 实验研究

本实验使用空气-水两相流，在室温20 ℃、标准大气压下展开。如图1[5]所示，实验系统主要由空气压缩机、气相回路、离心泵、水箱、液相回路、两相混合腔、气水分离器、实验本体和测量系统所组成。其中，水箱容量为1 m3，两相混合腔为双环空腔结构的两相注入系统，实验管道内径为50.8 mm，测试段长径比为66，气流量由转子流量计测量，精度为±3%，水流量通过电磁流量计测量，精度为±5%。实验中，气相表观速度(jg)为0.01～4 m/s，液相表观速度(jf)为0.2～4 m/s。

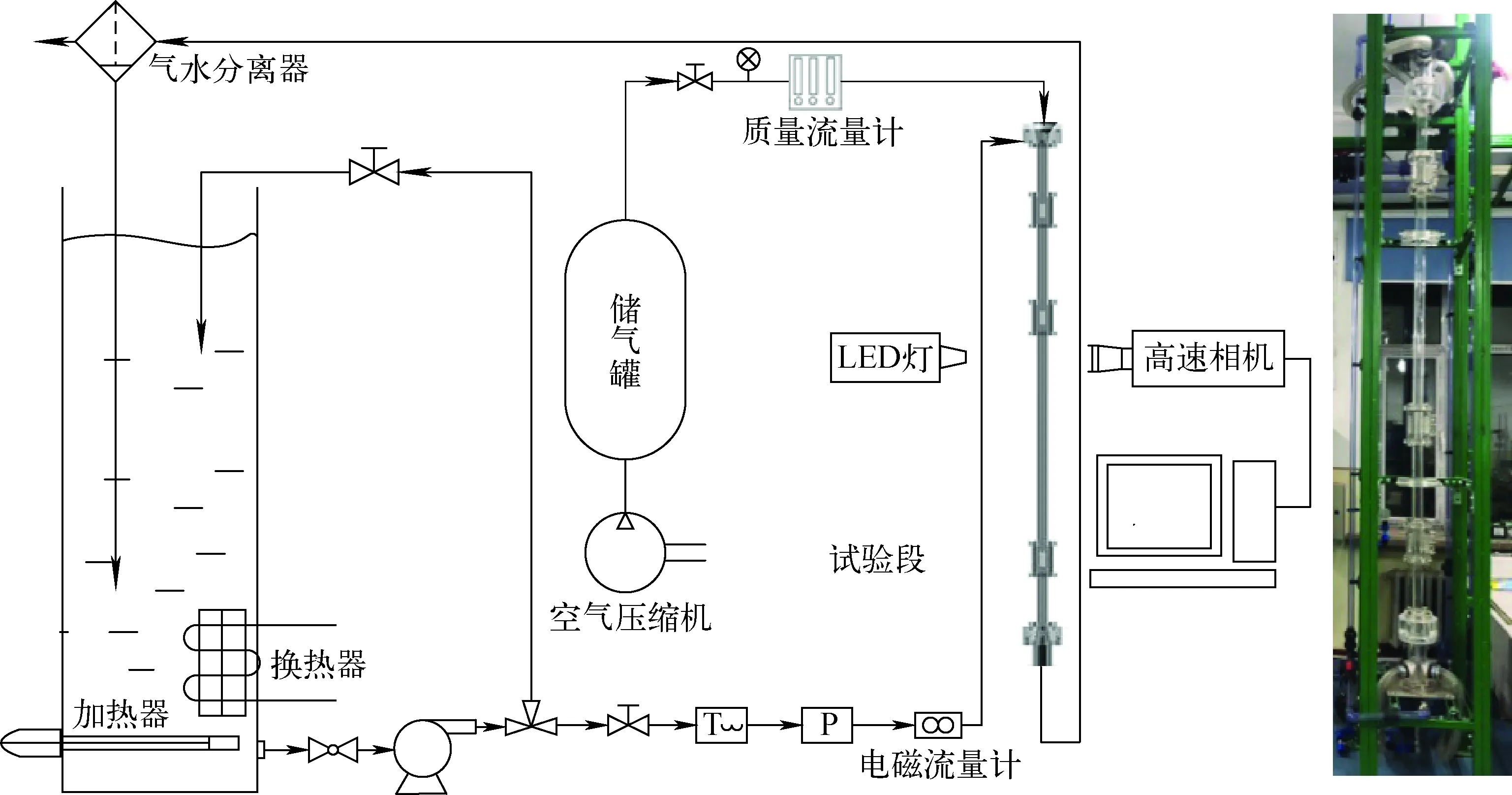
图1 实验系统示意图Fig.1 Schematic diagram of test facility

实验过程中，空气先通过气体压缩机压缩至0.7 MPa，然后引至实验本体顶部的两相混合腔与引自水箱的去离子水混合，最终进入实验本体实现自上而下的流动。在经过试验段后，进入气水分离器，经过分离后的气体直接释放到外部环境，去离子水则通过水管回路返回水箱。

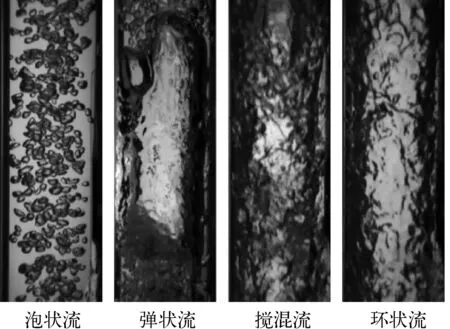
图2 竖直下降两相流流型 Fig.2 Two-phase flow regime in vertical-downward tube

图2为作者研究所获得的竖直下降两相流流型，主要分为泡状流、弹状流、搅混流和环状流4种典型流型[5]。其中，泡状流的气泡大小均匀，呈椭球状或球状，分散于连续液相中。弹状流中有细长的气弹跟随在液弹的下游，这些气弹通常有一个偏心的头部，指向与流动方向相反的方向，并且它们的弦长大于管道直径。在尾部附近，小气泡从边缘被剪切掉，形成尾流区。搅混流中，高度扭曲的气段塞占据了整个管径，而连续的气段塞之间存在着高度混乱的液塞，在壁面附近形成了携带小气泡的波状液膜；此外，在尾流区还存在逆流现象。环状流中，连续气相夹带液滴在管道中心流动，壁面附着有一层连续且呈波浪状液膜。

对实验所选工况的流型绘制流型图及流型转换边界，如图3所示。从图3可看出，不同流型之间有着高度的非线性可分特性。

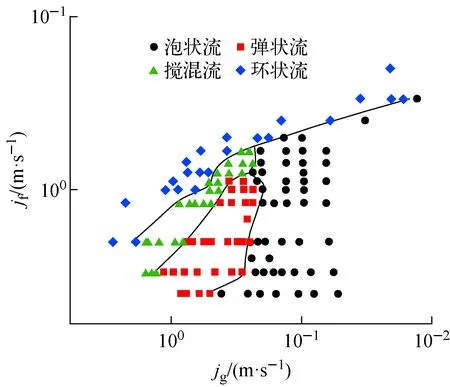
图3 流型与转换边界Fig.3 Flow pattern and conversion boundary

2 模型建立

2.1 RF分类

RF算法[14]在以决策树(decision tree, DT)为基学习器构建Bagging[21]集成的基础上，进一步在决策树的训练过程中引入随机属性的选择。该分类模型的原理是利用与决策树相同的树状结构，将数据记录进行分类，树的1个叶结点即代表某个条件下的1个记录集，根据记录字段的不同取值建立树的分支[22]。

对机器学习中的决策树而言，如果带分类的事物集合可划分为多个类别中，则某个类(xi)的信息可定义如下:

I(X=xi)=-log2p(xi)

(1)

其中:I(X)为随机变量的信息；p(xi)为xi发生时的概率。

为克服决策树对样本空间过度分割导致过拟合的问题，RF使用Bagging方法集成决策树，通过对若干个单个的决策树分类器经过特定的结合策略形成了1个强分类器模型。RF在训练决策树模型的过程中，增加了随机属性的选择，经过n个决策树训练后，使每个分类结果进行投票决出最终类别。其绝对多数投票法的投票过程可如式(2)所示：

H(x)=

(2)

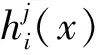
过拟合的主要原因是模型学习了太多样本中的随机误差。因为RF随机选择了样本和特征，并且将很多这样的随机树进行了平均，这些随机误差也随之被平均，乃至相互抵消。因此，RF有效防止了过拟合的问题，并能显著提高分类精度。

2.2 流型图扩展

实验中所得到的两相流型图为经验流型图，其两相流流速均处于低流速(0～4 m/s)区，无法满足实际生产应用。RF可通过已有的数据对样本集外的区域进行预测，实现流型图的扩展。

对于这类样本集外区域的特征，称作超范围特征，不同的超范围特征所组成的情况称为超范围情况。对于流型图这类的二维图表主要有单一特征扩展以及多特征扩展，需对原本不需划分训练集和测试集的数据进行分类。

图4 超范围特征Fig.4 Classification of beyond condition case

如图4所示，本文将特征值高区作为未知的空白区域测试集，然后进行训练与预测，这样训练的模型才能有效对超范围特征预测，且可初步判断流型图扩展之后是否可靠，提高扩展后流型图的准确率与可信度。

2.3 RF参数优化

由于需实现流型图的扩展，RF分类算法默认的方式精度较低。除对其参数与训练集进行一定的优化选取外，还需对其参数进行优化。

RF分类算法有两个重要的参数：叶子数(MinLeaf)和树数(nTree)，分别代表着叶子节点的最小样本数目和指定RF中分类器的个数。传统RF算法优化中大多使用穷举法、网格搜索法和交叉验证法。穷举法和网格搜索法效率低下，而交叉验证在小样本情况下会过高估计参数值[23]。

利用AFSA寻找最佳MinLeaf、nTree以及训练集与测试集划分的RF分类模型主要流程如图5所示。

图5 AFSA-RF模型流程Fig.5 Process of AFSA-RF model

主要涉及以下步骤。1) 划分集合：按照所需流型特征域与已有特征域关系依照超范围特征分类法，随机划分训练集和测试集。2) 种群初始化：随机生成系列MinLeaf、nTree初始人工鱼群。3) 人工鱼觅食、群聚与追尾：人工鱼随机在范围内选择新的点进行觅食，如果满足条件向其靠近1步，探索周围邻居鱼的最优位置，当最优位置的目标函数值大于当前位置的目标函数值并且不是很拥挤，则当前位置向最优邻居鱼移动，否则继续觅食。4) 选择操作：若满足人工鱼群中止条件，输出最佳MinLeaf、nTree参数组合，否则重新进行觅食、群聚与追尾行为直至找到最佳MinLeaf、nTree。5) 精度检测：将最佳MinLeaf、nTree组合输入RF模型进行测试，判断是否满足精度要求。6) 建立AFSA-RF模型：若符合精度要求，记录最优MinLeaf、nTree参数和特征子集组合以完成模型建立并开展预测集分类预测。

3 模型训练与结果讨论

3.1 模型训练

如图6所示，采用2.2节所述超范围情况选取法选取实验工况145组，其中设置训练集与测试集比例接近7∶3。训练集中流型占比：泡状流，38.6%；弹状流，22.8%；搅混流，15.9%；环状流，21.8%。测试集中流型占比：泡状流，36.4%；弹状流，22.8%；搅混流，18.2%；环状流，22.8%。将jg、jf、雷诺数(Re)、施密特数(Sc)4个基本特征及其经过简单计算处理所得的处理特征作为特征输入，将流型标签作为网络输出，其中，流型标签为泡状流、弹状流、搅混流、环状流。

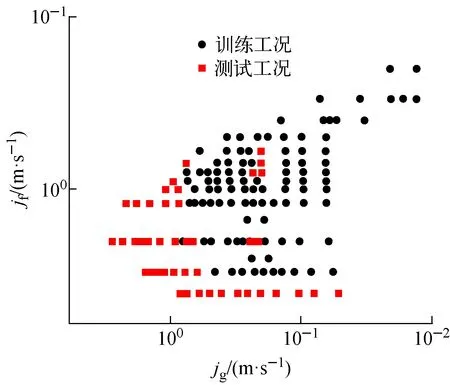
图6 工况数据选取Fig.6 Working condition data selection

网络训练前，对数据初始化参数。设置MinLeaf、nTree的参数组合寻优范围为[1，20]与[1，300]，生成鱼群规模10，最多迭代次数300，最多试探次数10，感知距离1，拥挤度因子0.618，步长0.1。参数寻优过程中RF训练目标准则设置为PRF_for_AF≥170，PRF_for_AF的表达式为：

(3)

(4)

其中：Ptrain为模型训练的精度；Ptest为模型对超范围特征区域预测精度；Pdifference为二者之差。该式既能要求两个精度均达到较高水平，又可在保证不过拟合和欠拟合的情况下使对超范围特征区域预测精度尽可能高，以达到对高流速区域精准预测。在满足上述条件下，基于AFSA优化RF的袋外失误率变化情况如图7所示，随着迭代次数的增加，袋外失误率也逐渐减小并趋于范围收敛，表明优化模型参数设置得当，训练效果较好。此时最佳MinLeaf、nTree分别为9、83。此时，AFSA-RF模型针对当前特征子集的训练精度和测试精度分别为93.07%和90.91%。

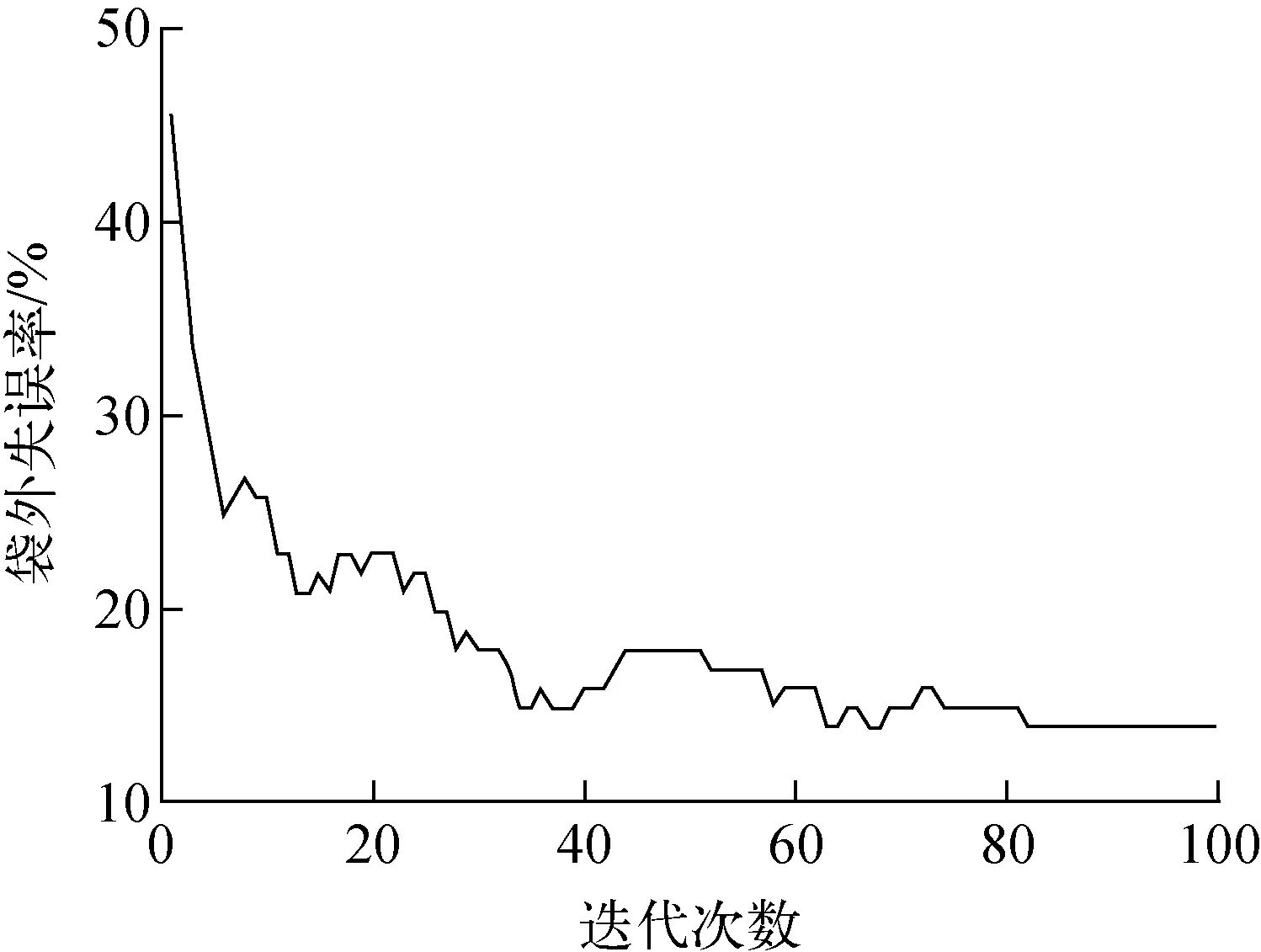
图7 袋外失误率Fig.7 Out of bag error

3.2 结果讨论

RF模型中影响因子为袋外观测置换变量增量错误(OOBPermutedVarDeltaError)，其定义为均方误差与标准差之比，其定义式为：

OOBPermutedVarDeltaError=

(5)

利用最佳MinLeaf、nTree和特征子集组合构建优化模型并实现预测集中流型分类，经过AFSA-RF模型训练之后，如图8所示，得出影响因子最大的3组特征值依次是气/液流速之比、气相流速和液相流速。流型图绘制通常以气相流速、液相流速为坐标，故本文选用气、液表观流速及气液两相流速比这3个特征作为特征输入。

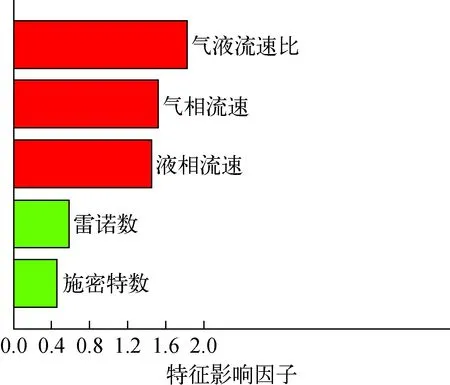
图8 特征影响力排序Fig.8 Ranking of influence characteristic

通过训练集数据构造的预测模型对所有原始数据的预测结果列于表1，其中错误流型全部位于流型转换边界线附近，本文认为造成这一现象的原因是转换边界处流型特征向量间区别较小，交叉重叠的杂糅信息过多。其中弹状流的精度最低的原因主要是由于它与其他3种流型均有转换边界，容易使模型误判。

表1 原始数据预测结果Table 1 Forecast results of original data

通过按照2.2节与3.1节所述方法选择的训练集数据构造的低流速区域(jg≤2 m/s，jf≤4 m/s)预测模型所作的流型图及其与实际流型对比如图9所示。

通过全部数据构造的预测模型所作的低流速区域(jg≤2 m/s，jf≤4 m/s)和高流速区域(jg≤4 m/s，jf≤8 m/s)的流型图分别如图10a、b所示，从图10c可知，使用训练集数据得出的流型图与使用所有数据得出的流型图，仅因全部数据中多了一些转换边界附近的补充，使泡状流-塞状流转换边界有局部微调，但针对流速较高的部分，转换边界几乎完全相同。这说明本文提出的流型图扩展方法有效，可使用该方法进行高流速区域的流型预测并绘出流型图。在此流速区域的两相流体可通过直接读图或在已训练好的AFSA-RF模型中输入特征进行流型判断。

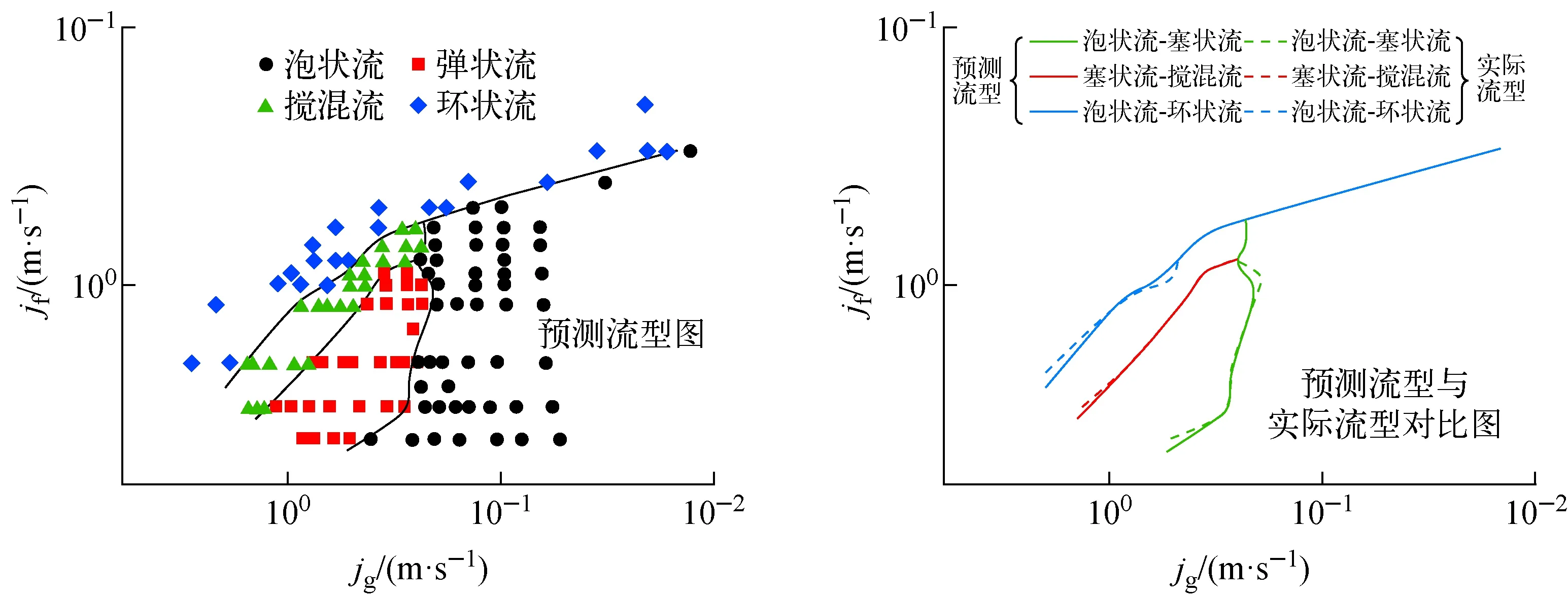
图9 训练集数据构造流型图Fig.9 Flow pattern graph by partial data

a——低流速区域流型图；b——高流速区域流型图；c——全部数据与训练集数据模型对比图图10 全部数据构造流型图Fig.10 Flow pattern graph by all data

重复计算10次后，经过优化后的RF模型的平均训练精度与测试精度分别为91.08%和89.55%，未优化的RF模型的平均训练精度与测试精度分别为77.20%和83.18%。由此可知，经过AFSA优化的RF模型训练精度和测试精度均更高，且在实验观察中发现未经优化的RF模型在第1、7、9组出现了较严重的欠拟合现象，在第8组出现了过拟合现象，稳定性远不如经过AFSA优化过后的RF预测模型。

为评估具体模型的有效性，在相同实验工况的前提下，对比了穷举法(enumeration method, EM)、交叉验证法(cross-validation, CV)、网格搜索法(grid search, GS)和AFSA 4类优化方法对模型的预测效果的影响。如表2所列，4种模型的训练与预测精度均在75%以上，但除了CV和AFSA-RF以外两种基本模型的预测效果较差。且GS和CV进行流型判断的模型，出现了较明显的欠拟合现象，这是传统参数优化方法的缺陷所在。EM虽然精度有了明显提升，但相比AFSA还有一定差距。

更高的精度预测使AFSA-RF更适合用于流型的预测与高流速区域超范围特征预测，获得高流速区域的流型图。但由于其设置了参数的目标准则来防止过拟合与欠拟合，而不是以完成次数或训练经度为准则，整个模型的计算时间远超过其他4种，高于最快的CV近55倍，故不适合直接作为在线预测模型，还需通过其他优化方法进行加速。

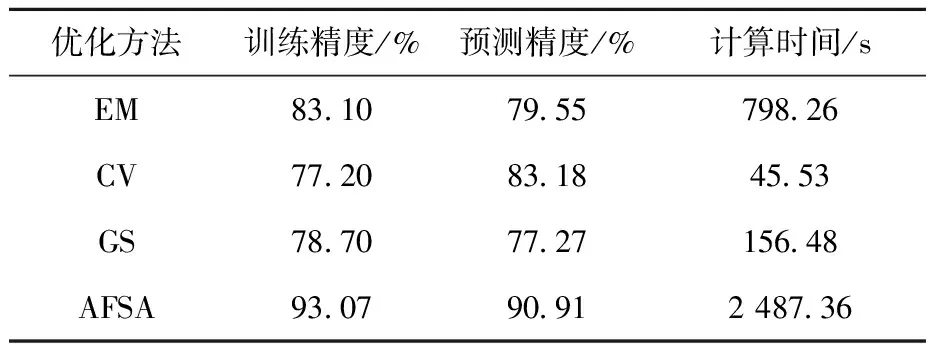
表2 不同优化模型流型预测结果对比Table 2 Results of different models

4 结论

本文通过竖直下降管内气-水两相流可视化实验，提出了AFSA-RF用于两相流流型图自动生成，通过超范围特征来划分相应训练集工况，将流型图向外扩展，实现两相流流型图自动生成；通过设置参数目标准则防止过拟合和欠拟合行为的发生，保证了预测合理性和准确性；通过人工鱼群加速获得合理的参数组合得到了较其他优化模型更高的训练精度与测试精度。