基于深度学习的减压音乐重构研究

李 哲 陈 宇 张 博 陈 亮 郭 滨

(长春理工大学电子信息工程学院 吉林 长春 130022)

0 引 言

随着社会现代化的发展，生活节奏加快给人们带来焦虑情绪。对于影响情绪的方式而言，音乐是非入侵的有效方法，其作用在临床应用上也得到了认可，研究表明音乐能够有效影响人的情绪[1]。

传统生成音乐的方法有概率模型[2]，由于音符被认为是无序的，重构音乐时忽略上下文的连接。现已有更多算法用于重构音乐，包括马尔可夫模型和遗传算法[3]。马尔可夫模型重构音乐时处理长时间序列会随着时间增加而衰减，遗传算法每次迭代延迟较高。在神经网络的基础上，音乐重构在深度学习上有更好的发展。重构音乐序列过程可以映射到深度学习算法上[4]。文献[5]为了解决循环神经网络(RNN)生成长时间序列时的梯度消失问题，利用长短期记忆循环神经网络(LSTM)生成鼓的节奏序列。通过训练LSTM网络可以生成指定风格的音乐，如Hutchings等[6]通过训练LSTM网络生成爵士乐，文献[7]基于BiLSTM和NN网络生成巴赫风格的曲子。但以上研究没有提出基于情感背景重构影响情绪的音乐。

临床上测评焦虑程度多采用汉密尔顿焦虑量表(HAMA)和焦虑自评量表(SAS)。文献[8]采用HAMA对66名重度抑郁焦虑合并症患者进行心理评估，以分析焦虑情绪与症状的因果关系。SAS应用于焦虑情绪疗效评估的效度信度高，适用于广泛人群测评焦虑程度[9]。

基于以上研究，本文提出重构减压音乐模型。对多轨道音乐进行减压特征提取，通过训练LSTM网络重构音乐，并分析重构的音乐质量,结合HAMA和SAS设计合理化减压实验，分析重构音乐的减压效果。

1 原理分析

1.1 频谱质心

频谱质心是音乐在频域上的特征，通过快速傅里叶变换(FFT)由音频转化到频域上分析音乐信号频谱包络的质心。频谱质心可以用来衡量乐曲中所含高频分量和低频分量的比重。频谱质心较低时，乐曲有较多低频内容，乐曲呈现的低沉阴郁品质，频谱质心较高时，乐曲有更多明亮舒缓的高频内容。频谱质心计算公式如下：

(1)

式中：N为帧长；k表示频率下标；Si(k)代表在第i帧信号位置的快速傅里叶在k处的幅度值。

1.2 栈式自编码器

自动编码器AE(Auto Enconer)是无监督学习的神经网络。AE的构建是基于反向传播算法，有输入层，隐藏层和输出层。输入层与输出层的神经元数量相同，隐藏层的神经元数少于输入层的神经元数。如图1所示，AE分为编码器(Encoder)和解码器(Decoder)两部分，x代表原始输入数据，h代表表征，r代表输出数据。编码器是输入层到隐藏层的数据处理过程，使原始数据x被迫降维，压缩成潜在的维度表征h，并能学习到样本数据的特征。解码器的过程是隐藏层到输出层，由于隐藏层的维数少于输出层的维数，输出数据r通过压缩数据的表征重新构造得到。此过程处理多维训练数据，提取更高的潜在特征。

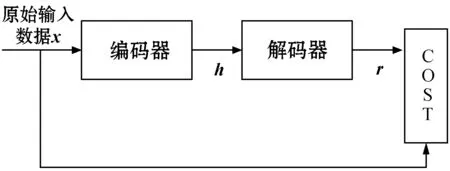
图1 自编码器结构图

编码器的函数表达式如下：

h=f(x)

(2)

编码过程激活函数使用sigmoid函数，表达式如下：

(3)

解码过程函数表达式如下：

r=g(h)=g(f(x))

(4)

用于数据重构的误差函数为均方误差函数(MSE)，表达式如下：

(5)

代价函数表达式如下：

(6)

式中：N为训练样本的数量；xi为输入向量；ri为自动编码器网络重构的输出结果。训练自动编码器网络的目的是学习输入向量xi与输出向量ri相似的关系，为了减小输出与原始数据的误差，训练代价函数使其值减小。

栈式自编码器(Stacked Auto Encoder，SAE)是堆叠多个自编码器构成[10]，又称深度自编码器。本研究使用的栈式自编码器结构是由两个自编码器嵌套组成，如图2所示。隐藏层的神经元数目是逐层减少的，前一层的输出是下一层的输入，通过深层压缩，提取潜在特征，二阶特征为此网络学习到和弦与旋律的更高维度的特征。

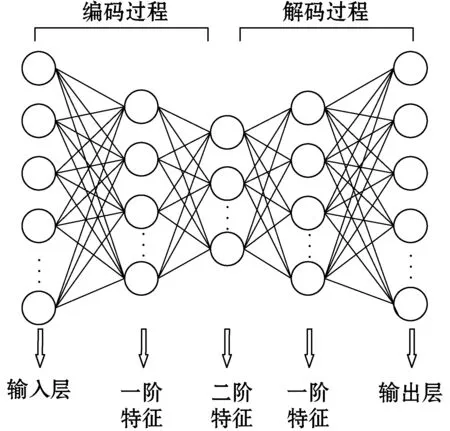
图2 栈式自编码器网络结构图

1.3 LSTM原理分析

循环神经网络(RNN)是闭合反馈神经网络，利用历史信息通过隐藏层的网络结构，影响当前处理的数据。但训练长序列的重构比较困难，主要原因在于向前传播和反向传播都会乘上多次隐藏层的参数。隐藏层参数小于1，导致前向传播中小于1的值乘上多次时减少对输出的影响，反向传播时会导致梯度弥散问题。在传统RNN的基础上，Hochreiter等[11]提出了长短期记忆循环神经网络(LSTM)解决RNN的梯度消失，改善长序列生成问题。

LSTM设计目的是通过使用常数误差流(CEC)来获得长时间的恒定误差流。LSTM通过“门”的结构遗忘和增强信息到神经元的能力，来记忆长期的信息，“门”是一种让信息选择性通过的方法。LSTM中历史信息存储在存储单元，更新和处理数据通过输入门、遗忘门和输出门控制。LSTM单元结构如图3所示。

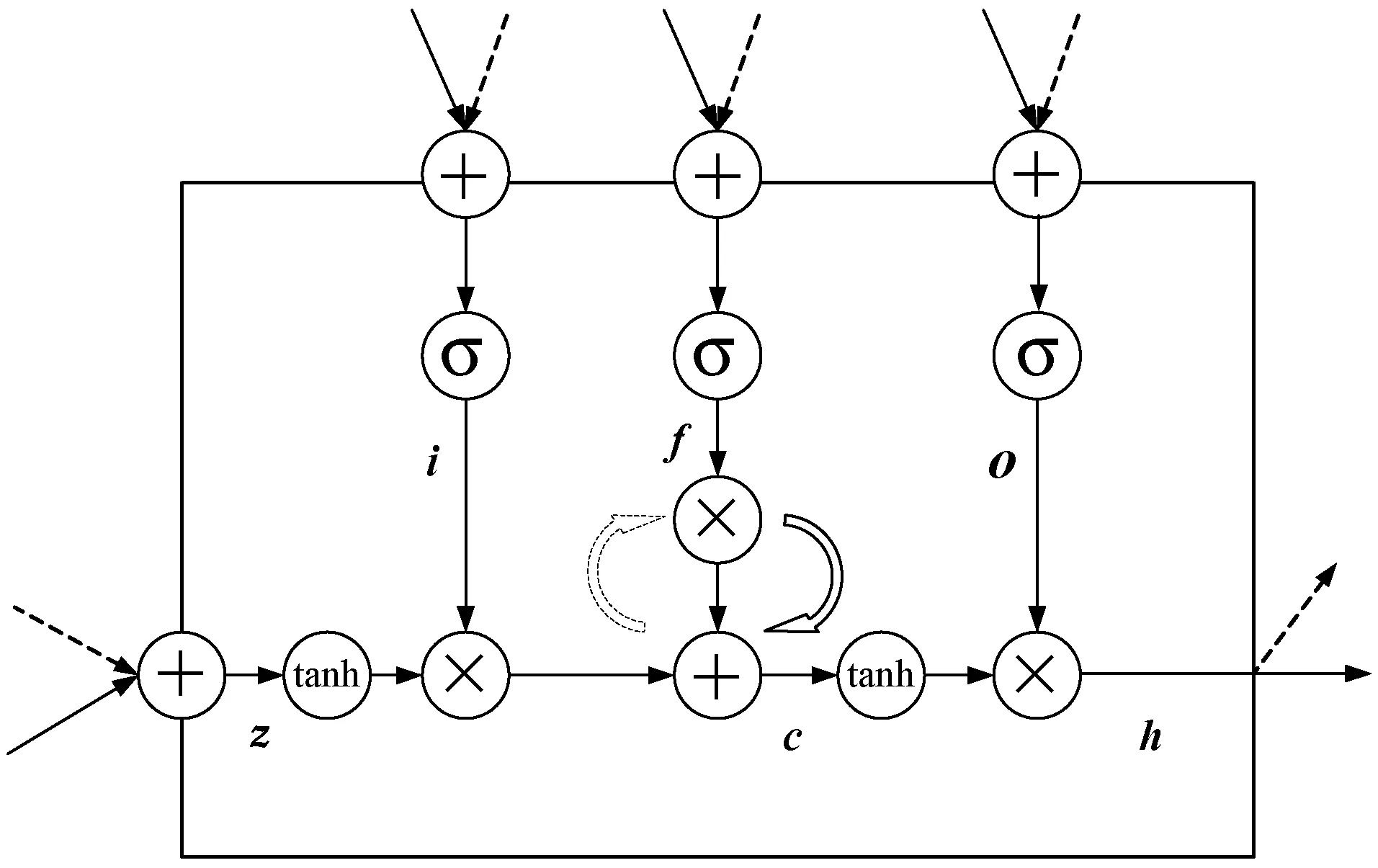
图3 LSTM单元结构图

时间步长t下的输入值为xt，隐藏状态值为ht，w为加权矩阵，b为偏置向量，σ为sigmoid激活函数。LSTM向前传播具体计算过程如下。

遗忘门的输入通过sigmoid函数，使其输出的值在0～1之间，1表示信息完全保留，0表示信息完全遗忘。遗忘门可以选择性遗忘神经元状态中无意义信息，控制历史信息对当前状态的影响。遗忘门计算公式如下：

ft=σ(wxfxt+whfht-1+bf)

(7)

输入门控制对当前神经元状态的更新，计算公式如下：

it=σ(wxixt+whiht-1+bi)

(8)

输出门控制储存单元的状态值的输出，计算公式如下：

ot=σ(wxoxt+whoht-1+bo)

(9)

t时刻候选记忆值：

zt=σ(wxzxt+whzht-1+bz)

(10)

t时刻记忆单元值：

ct=it×zt+ft×ct-1

(11)

t时刻输出值:

ht=ot×tanh(ct)

(12)

3 研究方法

3.1 音乐序列预处理

下载480首舒缓的MIDI(Musical Instrument Digital Interface)格式音乐，MIDI格式的音乐文件携带数字化音乐信息，每个轨道表示一种乐器，准确记录每个乐器的演奏过程。由于节奏和调式影响音乐对情绪的引导，筛选出4/4拍慢节奏420首音乐，并转化成C大调音乐。将MIDI格式音乐转化为WAV格式的音频，音频通过快速傅里叶变换转换到频域，计算每首音乐的频谱质心。筛选出频谱质心高于平均水平的音乐，共360首音乐作为训练样本。

将频谱质心较高的360首音乐转化MIDI格式，每首音乐截取成90 s的音乐序列。在90 s的MIDI格式音乐中只保留钢琴、吉他、小提琴、短笛四个轨道，删除其他乐器所占的轨道。MIDI为各轨道的乐器定义出128个音符，编号为0～127，中央C编号为60。对每个音符演奏的力度定义编号为0～127。采用Python的music21包读取MIDI音乐文件的音符与和弦信息保存文本格式，通过One-hot编码生成128维向量作为训练数据。

3.2 减压特征提取

栈式自编码器用于提取频谱质心较高的音乐样本，提取各个乐器的和弦与旋律的潜在特征称为减压特征。前一层的输出即为下一层的输入，逐层训练之后再进行反向训练。通过已有数据对栈式自编码器进行预训练，在Tensorflow框架中构建栈式自编码网络，设置栈式自编码器输入与输出神经元数量相等，输出数据的维度与输入数据相同为128维，一阶特征层设置88维，二阶特征层设置64维。由栈式自编码器提取二阶特征层的数据即为潜在的减压音乐特征向量，用x表示。

3.3 音乐序列重构模型

将音乐特征向量x向左平移一个单位为y，即x=y。音乐特征向量输入LSTM，LSTM是用先前值预测下一个值，给出向量序列x<1>，x<2>，…，x构建模型预测y。通过不断迭代，得到的误差值传入LSTM反向传播中，更新加权参数w。输入向量是栈式自编码器的二阶特征层的特征向量，LSTM网络输入维度设置64维，隐藏层设置128维。为了防止过拟合，节点被丢弃概率(Dropout值)为30%，全连接层(Dense)神经元数等于输出音符不同的个数，通过Softmax预测LSTM单元的输出，输出的序列转换成一首5 min时长的MIDI音乐，完整音乐重构模型如图4所示。

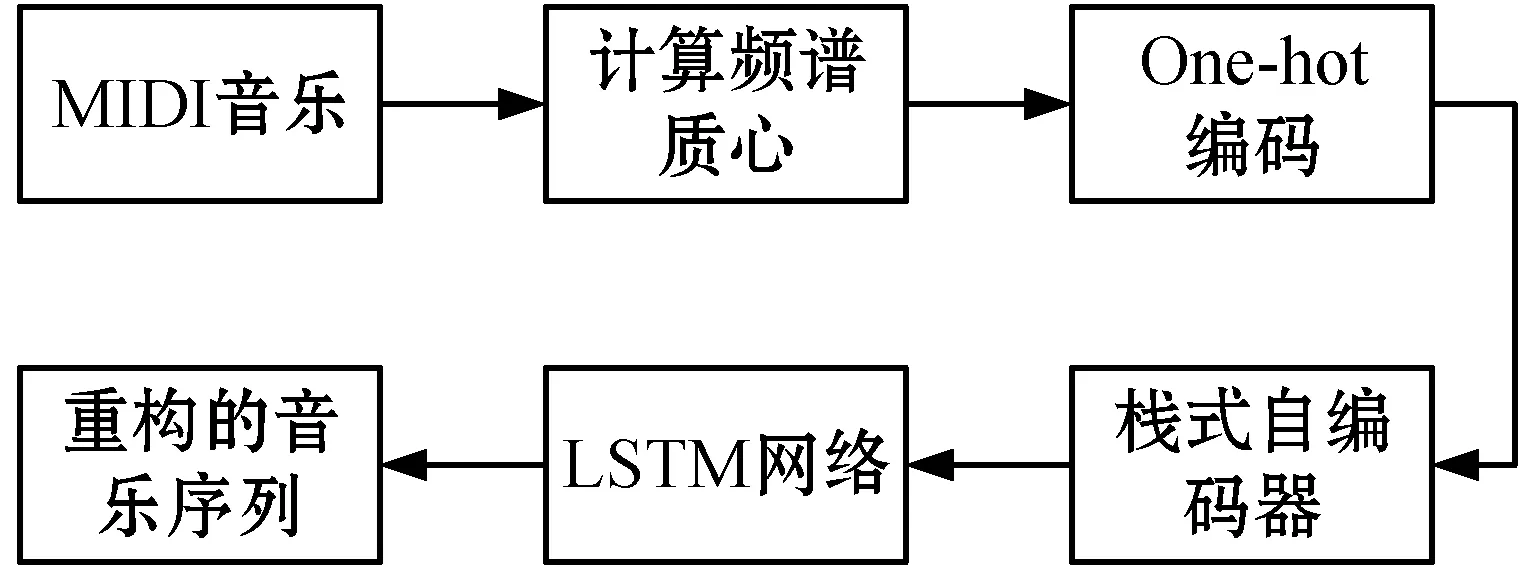
图4 完整音乐重构模型图

LSTM网络的隐藏层层数分别选择2、3、4层进行训练，LSTM网络层数等于隐藏层层数，迭代次数对训练结果的影响如图5所示，其中横坐标为迭代次数，纵坐标为损失函数的值。

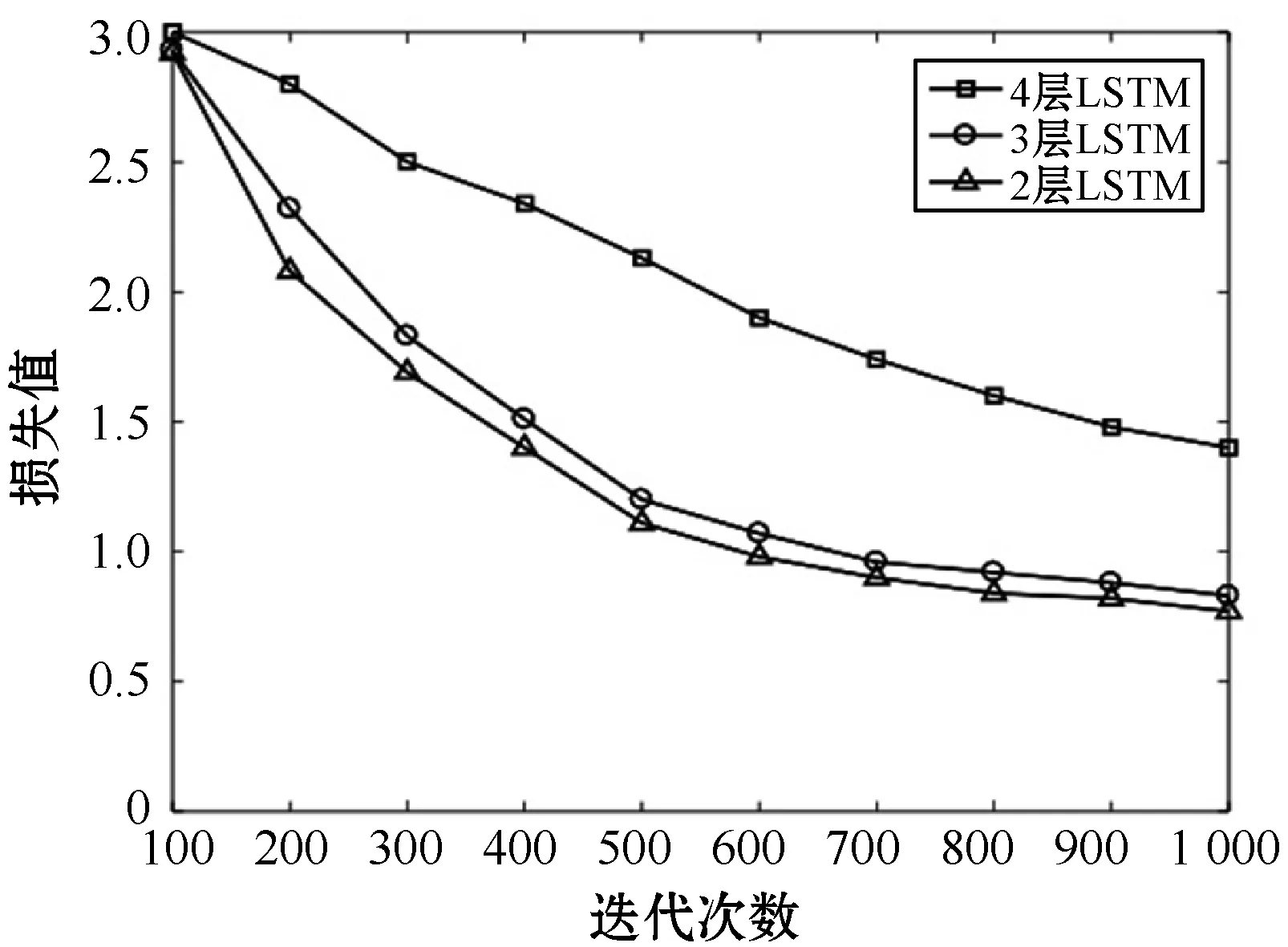
图5 不同层LSTM网络的损失值

LSTM网络层数设置过多时，梯度下降明显速率缓慢，3层LSTM网络收敛效果较好。重构音乐模型的生成音乐序列部分设置3层的LSTM网络。

3.4 重构音乐结果分析

3.4.1重构音乐的和谐度

重构音乐采用单独LSTM网络和加入SAE结构的LSTM网络(以下称SAE-LSTM网络)分别训练，设置产生相同的随机种子用于两种模型重构音乐，分别重构100首音乐作为音乐质量分析。

为了评定重构音乐的多轨道之间的和旋配合，对生成的音乐进行和谐度分析，轨道之间演奏相似的和旋则说明音乐和谐。和谐度计算公式为：

(12)

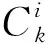
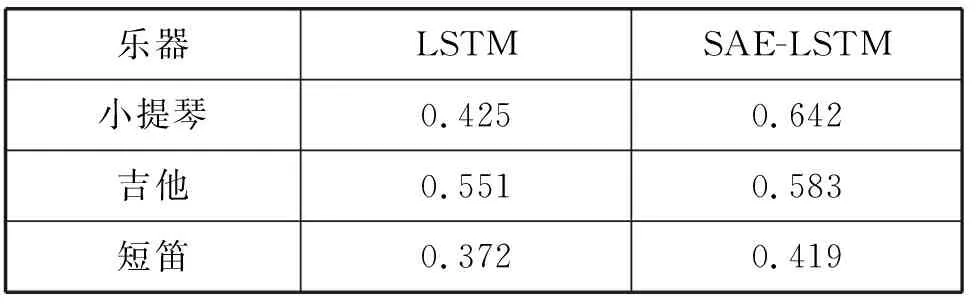
表1 重构音乐和谐度平均值

SAE-LSTM网络重构音乐较单独LSTM网络重构音乐的和谐度更高，结果说明SAE对音乐特征的提取可使LSTM网络在多轨道音乐上学习效果更好，重构的乐曲中各乐器之间搭配更和谐。

3.4.2重构音乐的音符分布均方误差

评估重构音乐模型学习乐器特性的效果，通过音符分布均方误差来衡量。乐器特性含义为每个乐器有独自分布的音域，例如钢琴有88个琴键，音域为A2-c5，而小提琴多演奏高音，音域为g-c4。音符分布均方误差越小说明重构音乐的模型学习效果好，计算公式为：

(13)

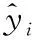
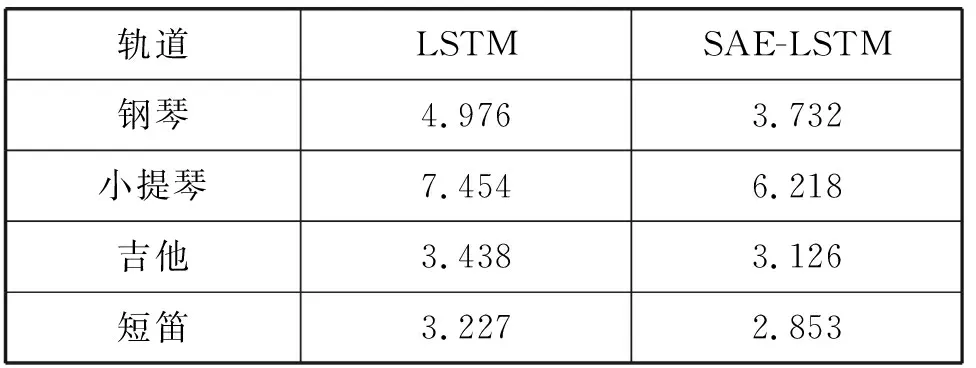
表2 重构音乐音符分布均方误差 (×10-4)

结果表明，SAE-LSTM网络重构音乐的音符分布均方误差较小，SAE对音乐特征的提取有效提高LSTM网络学习不同乐器的特性，从而提高重构音乐的质量。

3.5 重构音乐减压实验设计

3.5.1实验条件及对象

招募本校由自感由压力引发焦虑状态的志愿者30人，年龄20～24岁，均听力正常且受过音乐训练，告知实验内容均同意作为受试者参加减压实验。减压实验在心理治疗室中进行，保持室内安静和整洁并设置音响、耳机设备。

3.5.2测评指标

由于压力引发焦虑症状，通过受试者测评焦虑自评量表(SAS)和汉密尔顿焦虑量表(HAMA)的方式判断受试者的减压情况。SAS含有20个项目测评，每个项目有4个程度的选项，选项分值为1分、2分、3分、4分。计算测评总分数，总分在50以下表示没有焦虑症状，50～59为轻度焦虑，60～69为中度焦虑，69分以上为重度焦虑，分数越高代表焦虑程度越显著。HAMA包含14个项目，每个项目为0～4分五级评分法，总得分7分以下表示无焦虑，大于7分代表有明显焦虑，大于21分为严重焦虑。情绪越焦虑，测评出的分数越高。

3.5.3实验过程

通过计算频谱质心，由SAE提取减压特征输入的LSTM网络重构100首音乐，音乐总播放时长为342分钟52秒。30名受试者依次单独进入心理治疗室中，测评SAS与HAMA并记录得分情况。受试者被引导闭眼，坐于沙发以舒适姿势随机聆听重构的减压音乐，播放时长为十分钟。间歇三分钟，再次随机播放减压音乐十分钟。受试者聆听结束后，在无人干预的情况下再次测评SAS和HAMA，并记录得分情况。

3.5.4重构音乐减压效果分析

30名受试者依次参与完成上述实验过程，为了提高实验结果的效信度，记录减压音乐干预焦虑情绪前后的SAS与HAMA得分情况并分析，如表3所示。其中N代表参加实验的受试者人数。受试者在实验开始之前焦虑情绪均为显著，在聆听减压音乐之后焦虑情绪得到舒缓，根据每个人对音乐感知不同，减压效果也有所差异。得分情况表明该方法重构的音乐有效调节焦虑情绪，达到减压效果。

表3 减压音乐干预前后的SAS与HAMA得分

4 结 语

本研究提出多轨道减压音乐特征的提取方法，构建重构减压音乐模型。计算样本音乐的频谱质心，通过栈式自编码器对频谱质心较高的音乐进行特征高维度压缩，提取的音乐特征为减压特征，将特征输入LSTM网络训练重构减压音乐序列。在研究中发现栈式自编码器提高了LSTM网络对音乐特性与和弦搭配的学习，重构的多轨道音乐和谐度更高。设计减压实验，实验结果表明本文方法重构的音乐序列有减压效果。