一种电动汽车用PMSM速度电流单环控制方法

任核权 王洪亮 莫俊雄 陈烨洪 李 科 杨剑峰

1(绍兴大明电力设计院有限公司 浙江 绍兴 312000)2(国网绍兴供电公司 浙江 绍兴 312000)

0 引 言

电机与控制技术是电动汽车的关键部分，随着电力电子技术的飞速发展以及控制理论的深入研究，交流电机的控制性能得到了极大提升[1]。由于永磁同步电机具有高效性、大的扭矩-转动惯量比例和高功率密度等优点，被广泛用于电动汽车的驱动系统[2-3]。目前已经有很多非线性方法应用在PMSM的控制上，例如，滑模控制好、模型预测控制和自抗扰控制等[4-5]。

传统的PMSM的向量控制方法一般是级联型控制结构，即内环电流环、外环为速度环[6]。近年来，随着技术的发展，速度环和电流环之间的控制周期正在逐渐减小，甚至消失了。这样就使PMSM的控制方法不再只是级联型控制，将速度和电流放在一个环中进行调节的非级联控制方法也成为了可能。由于PMSM具有非线性、强耦合的特点，传统的级联型控制方法不能很好地解决PMSM的非线性控制问题，并且会影响到PMSM控制系统的瞬态响应。而且采用内环电流环和外环速度环的控制方法，虽然内环的稳定性和外环的稳定性分别得到了证明，但是两个控制器一起作用时，系统的稳定性却不能得到收敛性分析[7-8]。相比于级联型控制结构，非级联结构的控制方法具有能够实现直接控制速度、减少调节参数等优点。而且，非级联机构的控制方法可以提高PMSM可调参数的调节带宽。目前，有关PMSM非级联型控制的研究鲜有报道。文献[9]采用传统的PID单控制器，实现了速度和电流在一个控制器中进行调节的目标，而且所提出的单环控制方法相比于传统级联型PID控制方法，具有更快的响应速度。文献[10]采用终端滑模和一阶非线性扰动观测器的复合控制方法，实现了速度和电流的单环控制，相比于传统的滑模控制，所提复合控制策略具有更好的速度跟随性能以及扰动抑制能力。文献[11]采用有限时间控制和扩张状态观测器的复合控制方法，通过一个控制器实现了速度和电流的同时控制。文献[12]为了克服级联型控制结构的缺点，提出了新型模型预测控制方法实现速度的直接控制,将速度和电流离散化并预测未来的状态，经过仿真和实验证明了所提方法具有良好的跟踪性能。文献[13]消除了传统PMSM控制的级联型结构，提出了一种新型的直接预测速度控制方法，一种新型滑模面因子被引入到模型预测控制的代价函数中，一个控制器同时实现了速度和电流的跟踪控制，相比于传统的速度环采用PI控制器，电流环采用模型预测电流控制器的控制方法，稳态性能得到了提升。文献[14]证明了级联型PID控制器由于具有较小的内环时间常数，不能保证驱动系统的高动态性能。已有的研究已经证实了非级联结构的控制方法比传统的级联结构控制方法能够更好地处理非线性问题，所以电动汽车用PMSM的速度电流单环控制方法意义重大。

由于理想的PMSM数学模型中未考虑扰动及参数不确定性，所以当系统存在负载突变或电机参数不准确的情况，会导致电动汽车速度出现较大波动，甚至导致系统不稳定[15]。提高电动汽车用PMSM的扰动抑制能力在一定程度上可以提高系统的动态稳定性，近年来，如何提高PMSM的扰动抑制能力也成为了研究的热点问题[16]。文献[17]建立了PMSM驱动系统的多源扰动及不确定性的数学模型，将传感器和驱动器对驱动系统带来的影响考虑在了PMSM驱动系统的模型当中，相比于PID控制器和其他扰动观测方法，所提的扰动补偿技术极大地提高了跟踪精度及鲁棒性。文献[18]采用非线性扰动观测器估计PMSM驱动系统的匹配和不匹配扰动，采用端口控制的哈密顿控制方法实现PMSM的速度电流单环控制，当处理各类扰动的时候，所提的方法表现出了快速的速度跟随性能及强鲁棒性。当PMSM驱动系统中存在各种扰动和不确定时，文献[19]为了提高PMSM的驱动性能，提出了扩展滑模扰动观测器估计集总不确定性的方法，前馈补偿给系统，然后采用滑模控制实现PMSM的速度跟踪，提升了系统的鲁棒性。文献[20]提出PMSM驱动系统的PI调节器可以分解成闭环带宽和集总扰动带宽，并提出了两个带宽参数的优化算法，优化后的PI控制器使PMSM驱动系统具有更好的抗干扰性能。文献[21]采用扰动观测器对扰动和不确定性进行估计并补偿给系统，降低了非奇异终端滑模控制下的PMSM系统的控制抖振，系统的鲁棒性得到了充分的证明。现代控制系统在保证系统静态稳定性的前提下，应高度重视如何提高系统的动态性能，所以当电动汽车驱动系统存在扰动或参数改变时，尽量保持系统的运行性能出现更小的波动，有利于电动汽车舒适性。虽然针对PMSM的扰动估计和补偿方法有很多，但是几乎所有的扰动补偿方法都是针对级联型控制结构的PMSM驱动系统，非级联结构下的扰动补偿方法还需进一步研究。

本文主要研究电动汽车用PMSM的非级联控制策略，采用二阶非线性扰动观测器对系统的扰动及不确定性进行估计并前馈补偿给系统，采用非奇异终端滑模实现PMSM的单环控制。

1 永磁同步电机数学模型

为了简化分析，建立理想的表贴式PMSM数学模型，表示为：

(1)

式中：Ld和Lq分别是d轴和q轴电感；ud和uq分别是d轴和q轴电压；ψf是永磁体磁链；Pn是PMSM的极对数；id和iq分别是d轴和q轴电流；ω指电机的转速；R是电机的相电阻；B是摩擦系数；TL是负载转矩；J是PMSM动子转动惯量。由于本文考虑的电机为表贴式永磁同步电机，所以d轴电感等于q轴电感，定义L=Ld=Lq[22-25]。

本文所提的PMSM驱动系统的结构框图如图1所示，驱动系统包括表贴式PMSM、逆变器、SVPWM调制模块、clark变换模块、park变换模块、反park变换模块、速度位置检测模块、电流传感器，以及d轴和q轴控制器。

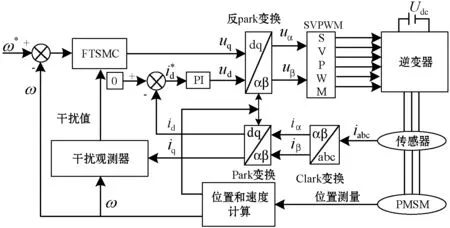
图1 PMSM控制系统结构

2 速度电流单环控制方法

2.1 控制系统线性化

本文采用id=0的控制策略，对于式(1),PMSM的运动方程可以表示为：

(2)

对式(2)进行求导后可得：

(3)

定义状态变量x1=ωref-ω，x1的微分可以表示为：

(4)

式中：ωref是速度参考信号。将参数不确定性及负载扰动考虑到系统中，运动方程可以转换为：

(5)

(6)

则x2的微分可以表示为：

(7)

考虑式(7)的参数不确定性，可得：

(8)

(9)

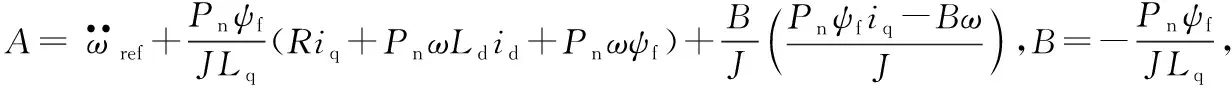
(10)

式中：R、Ld、Lq、J、B、ψf是标称参数；Rt、Ldt、Lqt、Jt、Bt、ψft是对应的实际参数值。ΔR=Rt-R，ΔLd=Ldt-Ld，ΔLq=Lqt-Lq，Δψf=ψft-ψf，ΔJ=Jt-J，ΔB=Bt-B。

PMSM的二阶运动方程的状态空间可以表示成：

(11)

则联立式(10)和式(11)，得到：

(12)

在实际的PMSM控制系统，电机的参数受运行环境的影响而改变，负载转矩也因实际的运行工况而不同，假设d1、d2及其导数都是有界的。

2.2 非线性扰动观测器

针对式(11)和式(12)设计二阶非线性扰动观测器，分别如式(13)和式(14)所示。

(13)

(14)

2.3 非奇异终端滑模的速度-电流单环控制策略

为了获得稳定的速度跟踪性能，设计二阶非奇异终端滑模面：

(15)

式中：β>0；p和q是正奇数，1

二阶非奇异终端滑模控制器的输出为：

(16)

式中：ε为切换增益系数。

(17)

3 仿真实验

3.1 仿真设计

通过MATLAB/Simulink环境对所提的二阶非奇异终端滑模(Non-singular terminal sliding mode control,NTSMC)控制器和二阶非线性扰动观测器(Second-order Nonlinear disturbance Observer,SNDO)的复合控制策略(NTSMC+SNDO)进行实验仿真,仿真用PMSM的参数如表1所示。

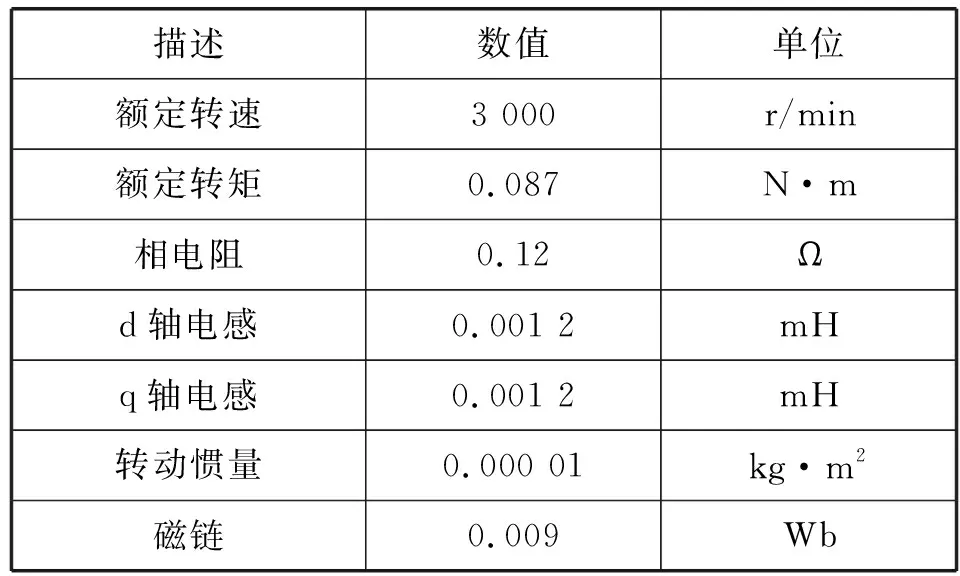
表1 仿真用PMSM参数

将本文所提的采用NTSMC+SNDO进行的速度电流单环控制方法与传统的级联结构的SMC控制方法进行仿真对比，分别进行了启动效果对比及突加负载的效果对比。三种控制器的d轴控制器参数设置相同，比例增益为1 000，积分增益设置为10 000。NTSMC的参数设置为ε=100，p=5,q=3,β=13。

PMSM的参考速度设定为1 000 r/min，PMSM初始启动时不带负载，本文所提出的非级联结构的NTSMC+SNDO与传统的级联结构的SMC和PID控制器进行对比，包括速度、d轴电流、q轴电流和A相电流等，对比结果如图2所示。

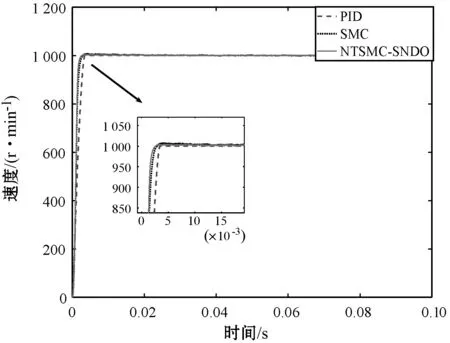
(a) 速度对比曲线

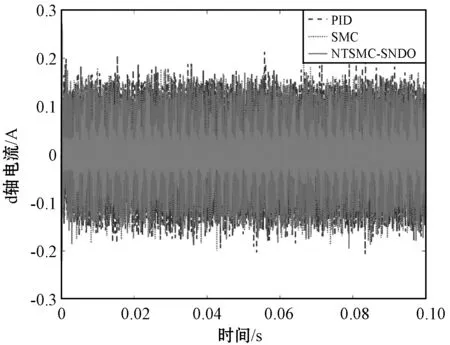
(b) d轴电流对比曲线

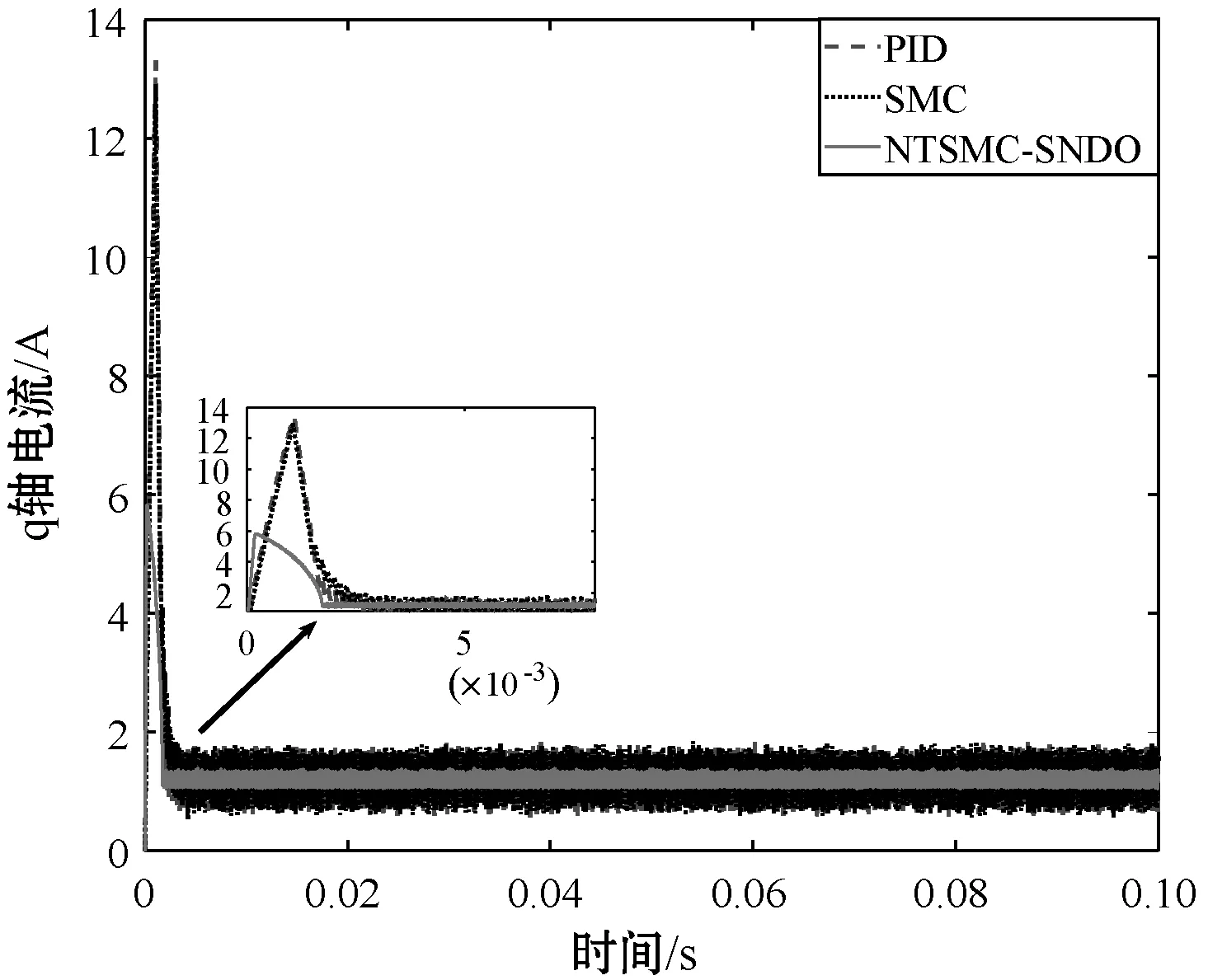
(c) q轴电流对比曲线

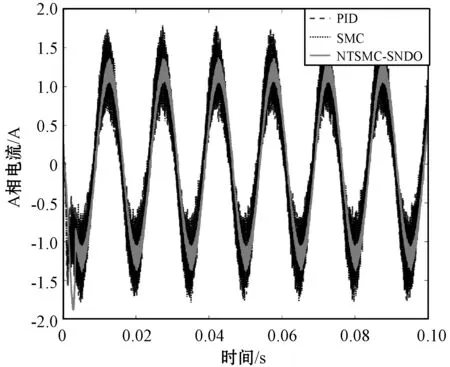
(d) A相电流对比曲线图2 PMSM启动时三种控制器的性能对比曲线

t=0.1 s时，负载转矩由0 N·m突然变为0.2 N·m；t=0.2 s时，负载转矩由0.2 N·m突变为0 N·m。采用非级联结构的TSMC+TNDO和传统的级联结构的SMC，PID控制器分别对PMSM进行控制，PMSM的速度、d轴电流、q轴电流、A相电流等对比曲线如图3所示。

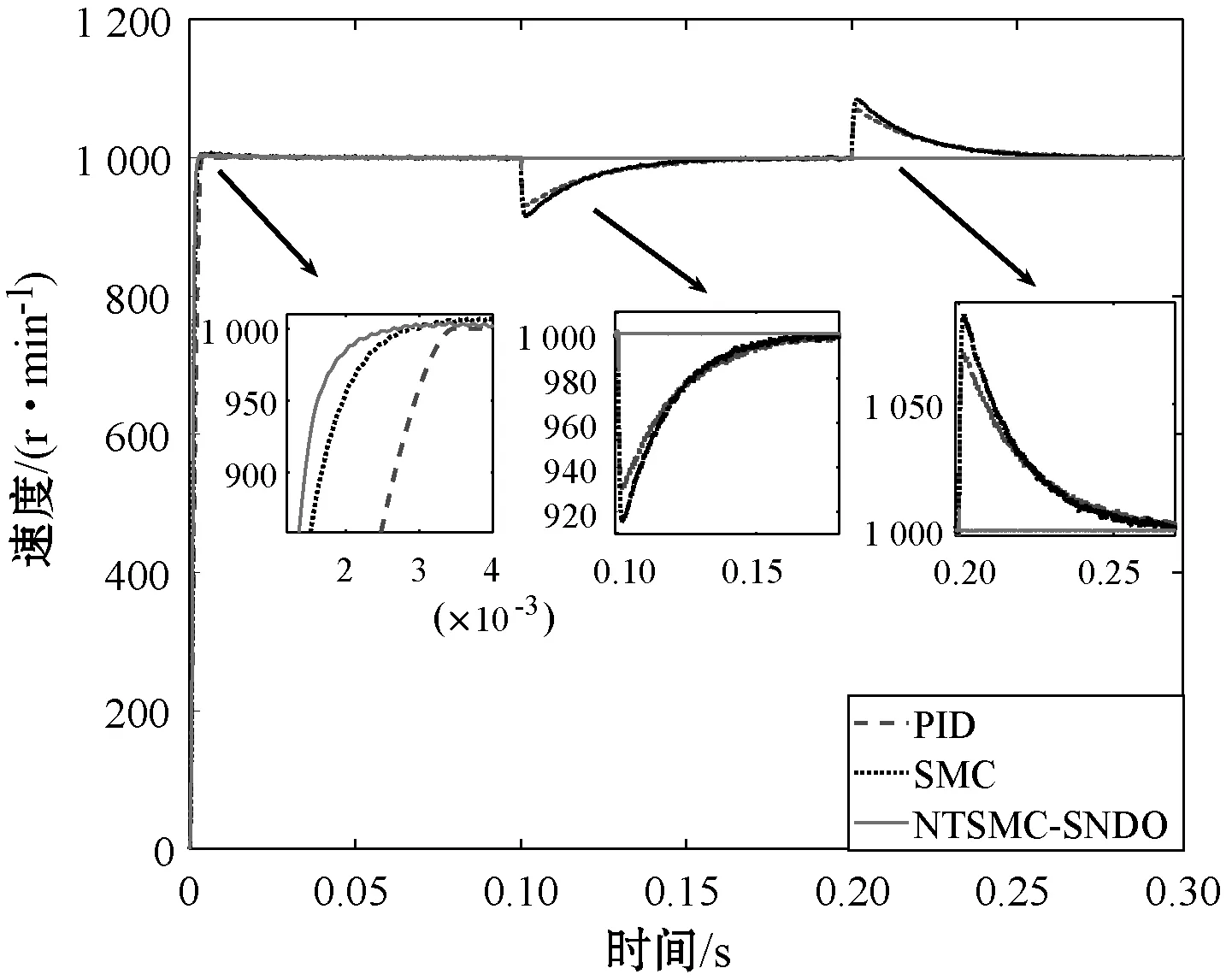
(a) 速度对比曲线

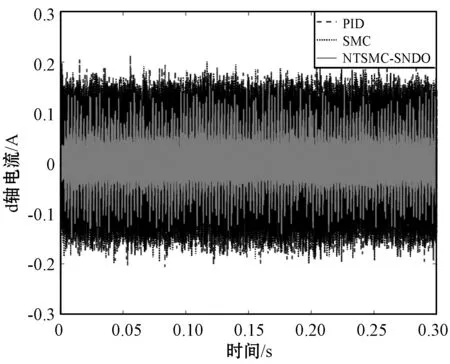
(b) d轴电流对比曲线

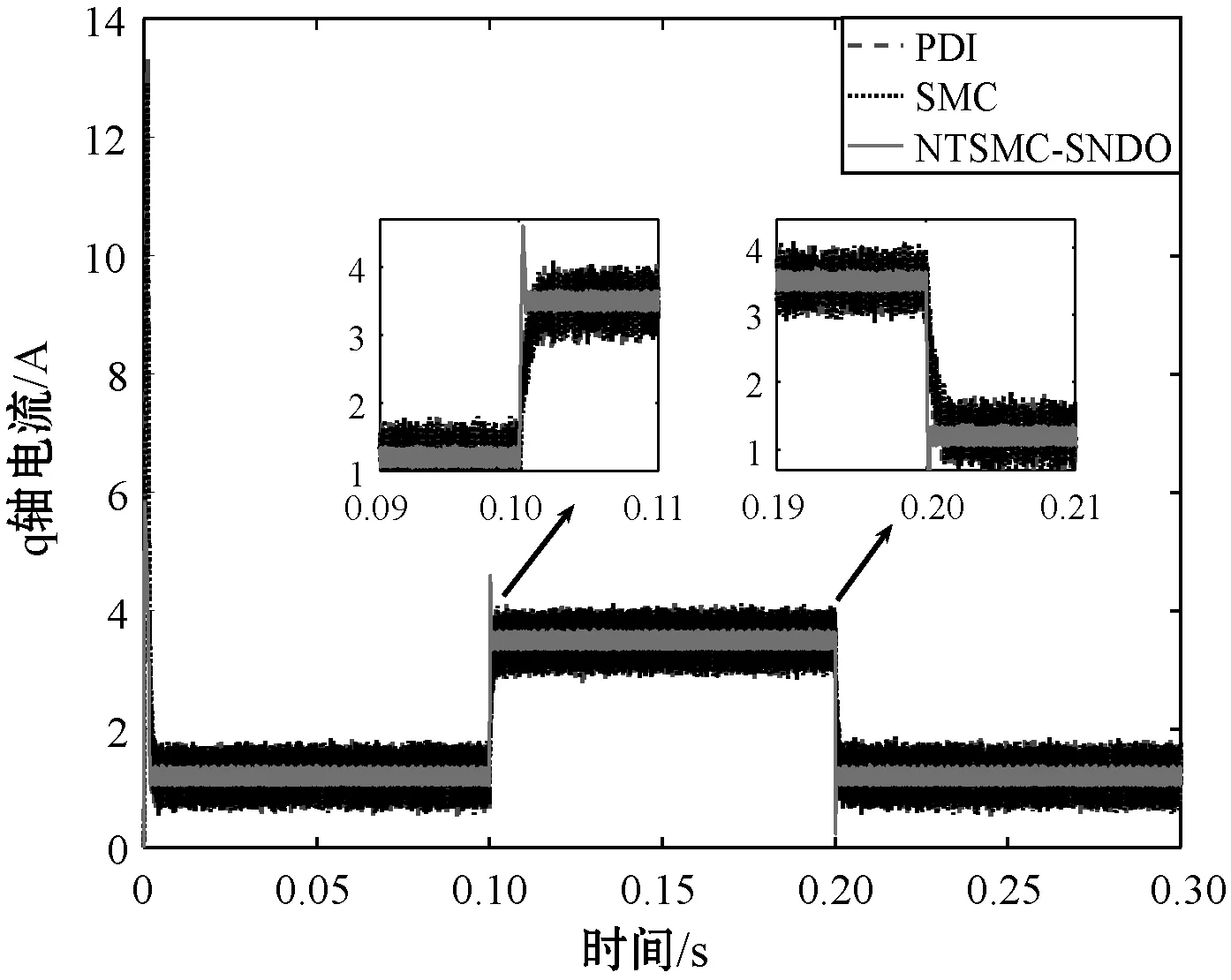
(c) q轴电流对比曲线

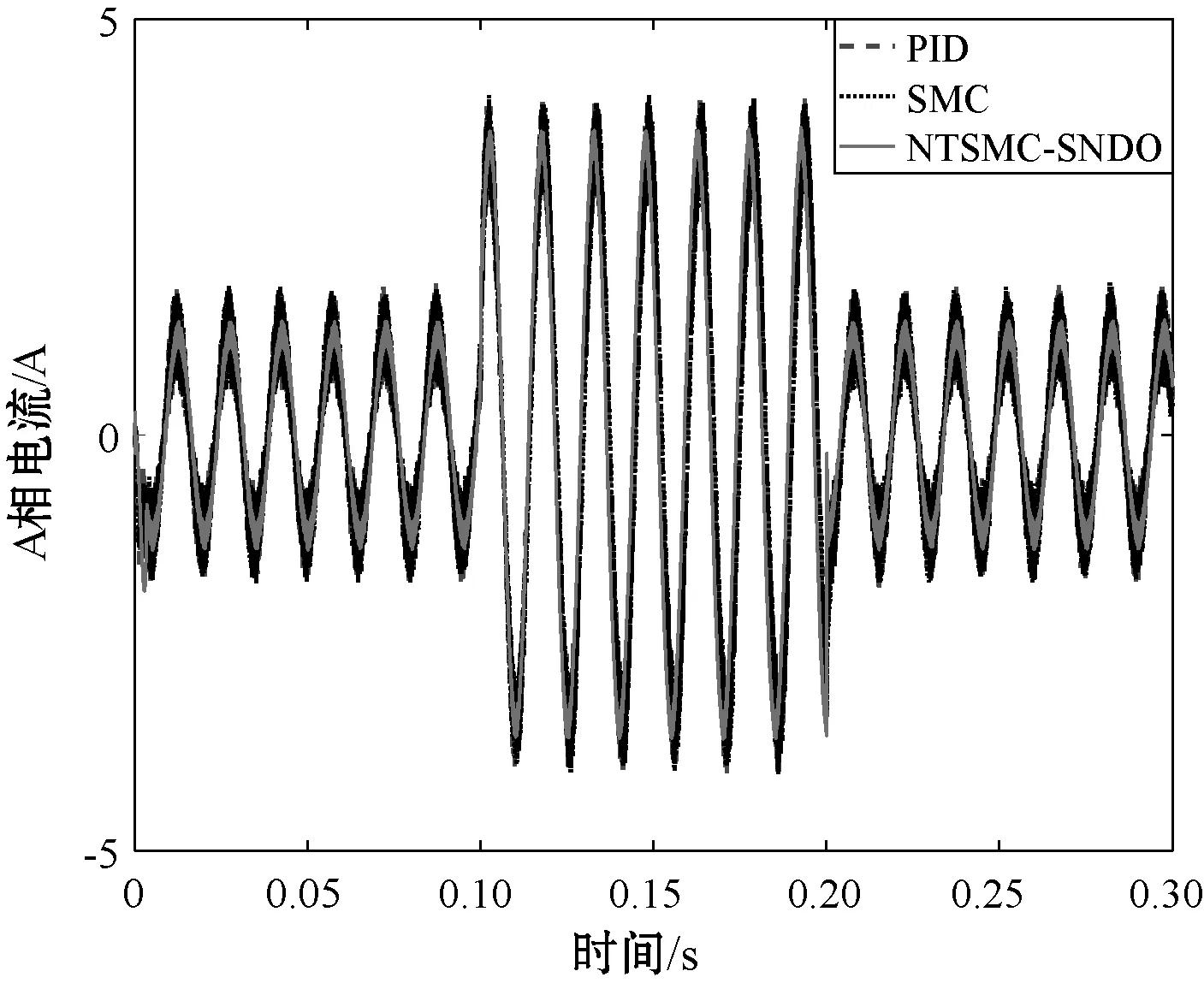
(d) A相电流对比曲线图3 PMSM突加负载时三种控制器的性能对比曲线

3.2 结果分析

从图2的PMSM启动阶段时三种控制方法的性能对比曲线可以看出，在没有超调的情况下，本文方法比传统的SMC和PID控制方法更快到达速度设定值。d轴控制器均采用PID控制器且参数设置相同的时候，NTSMC+SNDO的d轴电流抖动幅值明显小于SMC和PID的d轴电流。对比q轴响应曲线可以看出，NTSMC+SNDO的q轴电流比传统的SMC和PID控制器更快到达稳态值，且q轴电流的抖动幅值明显低于SMC和PID控制器的q轴电流。从A相电流对比曲线可以看出,NTSMC+SNDO控制策略下的相电流抖动小于SMC和PID控制器。

从图3的PMSM突加负载时的对比曲线可以看出，在突加负载和突减负载的时候，PID控制器的速度会从稳态值1 000 r/min增加或减少68 r/min，SMC的速度从稳态值1 000 r/min增加或减少80 r/min，而NTSMC+SNDO的速度从稳态值1 000 r/min增加或减少8 r/min，而且，NTSMC+SNDO的控制方法仅需要0.002 s恢复到稳态速度，而SMC和PID控制方法将需要0.06 s恢复到稳态速度，验证了本文方法极大地提高了PMSM的速度跟随性能。同样地，NTSMC+SNDO的d轴电流、q轴电流和A相电流比SMC和PID控制器具有更小的抖动。相比于SMC和PID控制器，NTSMC+SNDO控制下的PMSM的q轴电流更快到达稳态电流值。

4 结 语

本文提出一种采用非奇异终端滑模和二阶非线性扰动观测器的PMSM驱动方法，该方法可以实现一个控制器同时控制速度和电流，实现了速度的直接控制。PMSM驱动系统的集总扰动通过二阶非线性扰动观测器进行估计，并前馈补偿给系统，提高了系统的鲁棒性。仿真结果验证了本文控制策略具有更好的速度跟随性能。目前，还没有科学的非奇异终端滑模参数确定方法，未来可以从如何合理地确定控制器参数上进行考虑，以科学的理论指导提高控制效果，从而实现电动汽车的快速响应。