基于FP-growth算法的输电线路短路故障关键暂态信息检测
2022-09-06王普专张春香吴饰斐
王普专 邬 桐 周 磊 张春香 吴饰斐
1(国网福建省电力有限公司技能培训中心 福建 泉州 362000)2(东北大学 辽宁 沈阳 110819)3(国网辽宁省电力有限公司经济技术研究院 辽宁 沈阳 110015)4(北京科东电力控制系统有限责任公司 北京 100192)
0 引 言
伴随电力系统逐渐向大电网与高压电方面快速发展,用户对供电质量的需求也逐渐向高度可靠性靠拢。电力暂态信息存在比基波分量更丰富的故障信息,暂态信息的检测属于保护电力系统、定位故障的核心问题[1]。
由于故障暂态行波在线路中运行时存在非线性衰减问题,它的故障暂态信息未能完全被应用。如果可以完全发掘暂态波形的核心暂态数据,完成暂态故障情景透明式,便能够对故障原因实行高精度判定,让后续的输电线路优化与防御工作更具备针对性。输电线路故障所存在的暂态行波具有大量故障信息,比如极性、行波幅值、故障时间、故障方位、过渡电阻等[2]。以上故障信息属于输电线路故障诊断的核心凭据。当下国内外相关研究人员的分析大多集中于故障点暂态波形特征参数的提取,但是针对故障角、过渡电阻等暂态信息的提取,还未形成针对性的方法,此类暂态故障信息属于输电线路的故障原因判断的核心依据。为此,本文提出基于FP-growth算法的输电线路短路故障关键暂态信息检测方法,创新之处在于将基于FP-growth算法的频繁项挖掘方法应用于电力系统中,FP-growth算法能够快速采集相关数据,以免采集不相关数据对后期暂态信息提取存在干扰。当FP-growth算法采集输电线路频繁出现短路故障的线路信息后,通过故障关键暂态信息提取方法检测该输电线路短路故障角、过渡电阻等暂态信息,实现输电线路短路故障关键暂态信息的准确检测[3]。
1 输电线路短路故障关键暂态信息检测方法
1.1 基于FP-growth算法的频繁项挖掘方法
步入大数据时期,数据挖掘方法在互联网检索引擎、医药科学等很多领域被大量使用,主要用于在海量数据里发掘内在规律关联性、非无用信息。FP-growth算法属于数据挖掘方法在关联规则发掘领域的核心内容,能够快速挖掘数据集合中的频繁项集和数据间潜在关联规则。本文所用基于FP-growth算法的频繁项挖掘方法由FP-tree的构建和递归挖掘FP-tree两部分组成[4]。
1.1.1确定FP-tree支持度
FP-tree是一种输入数据的压缩表示法,它通过逐个读入事务,并把每个事物映射到FP-tree中的一条路径来构造。由于不同的事物可能会有若干个相同的项,因此它们的路径可能部分重叠。路径相互重叠越多,使用FP树结构挖掘的输电线路短路故障关键暂态信息效果越好。
设h={i1,i2,…,im}是由m个项组成的故障信息集合,D是一组输电线路短路故障数据集且D中事务数据都由h中的项组成。给定项集X⊆h在D中的支持数是指D中包含X的信息数,X在D中的支持度是指X的支持数占D中所有事务数的百分比。
定义1对于项集X⊆h,若X在D中的支持度sX大于等于给定的最小支持度s,则称项集X为事务数据集D在最小支持度s下的频繁项集。
定义2对于项集X⊆h,给定最小支持度s,若X的所有超集都是非频繁项集,则称项集X为事务数据集D在最小支持度s下的最大频繁项集。
若R={n1,n2,…,nm}为FP-growth数据集D生成的FP-tree中的一条路径,所有项集和路径都是按照支持度降序排列的。
证明:根据集合的性质容易得证,若X⊆R,由于所有项集和路径都是按照支持度降序排列的,则X⊄R。
通过上述证明可知,采用FP-tree的挖掘结构自顶向下的搜索策略,采用双重循环的方式挖掘最大频繁项集,若数据项集的支持度大于等于最小支持度阈值,则FP-tree适用于输电线路故障诊断中。
1.1.2基于数据集合构建FP-tree
FP-tree属于FP-growth算法的非常规数据结构,可保存输电线路短路故障原始数据中的相关数据,只采用2次数据扫描,便能将输电线路短路故障原始数据里的事务压缩至一个FP-tree中,此FP-tree与前缀树相似,相同前缀路径可通用,以此实现输电线路短路故障数据压缩[5]。
假定输电线路短路故障数据集A={a1,a2,…,am},a属于其中一条事务;随机事务aj属于输电线路短路故障多元素构成的组合,a2={b1,b2,…,bu},bu表示事务里的元素,本文将A设成例子,描述FP-growth的建立流程。
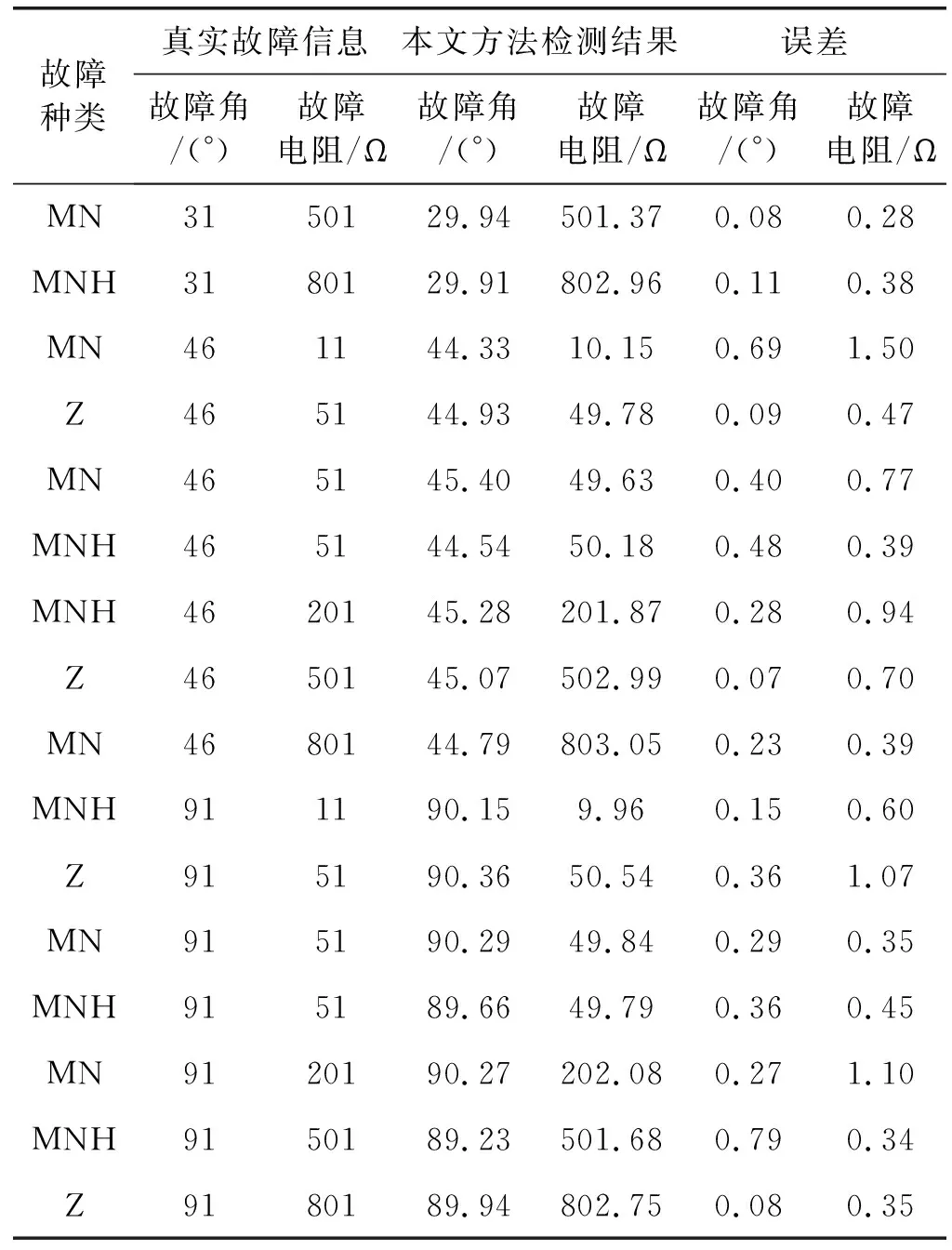
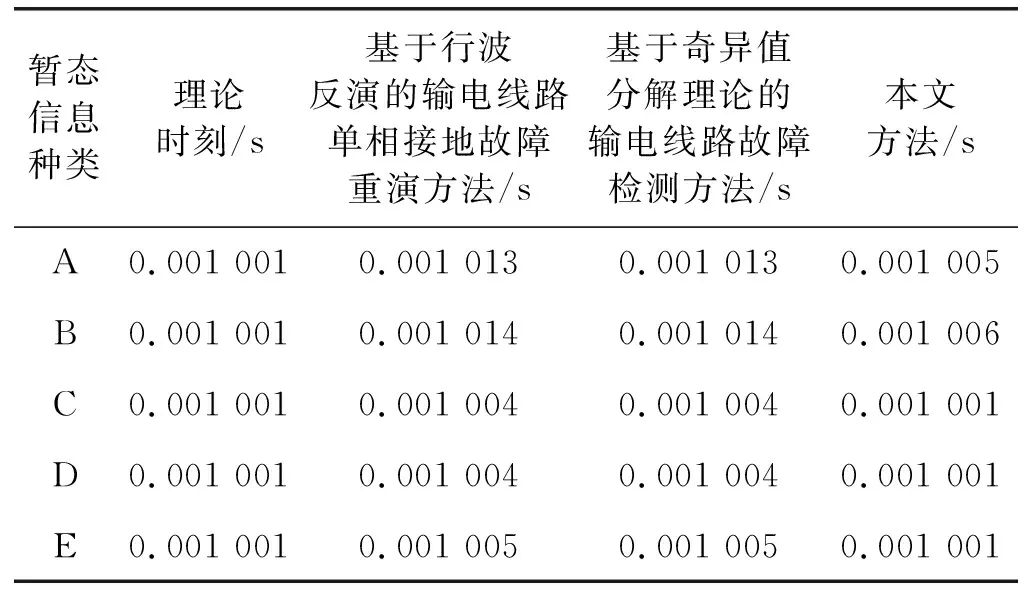
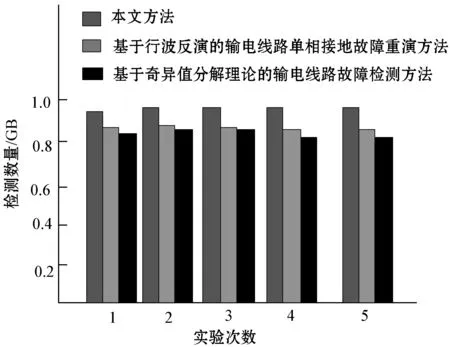
(1) 首次遍历输电线路短路故障数据集A,记载产生各个元素项bu的机率gu。把每个元素根据gu减序分布,之后把每个元素项bu标识信息和存在机率gu存储在头指针表Tabhead里;提前设定最小支持度gmin,如果gu (2) 再次遍历输电线路短路故障数据集A,对A中各个子集aj实行筛查与排序。先把aj里gu (3) 通过AM建立FP-tree。自空集开始,把AM中的每个事务aj逐个加入树中。先确定FP-tree里是否含有与事务aj一样的前缀分支:如果含有,那么共同前缀分支存在输电线路短路故障检测节点的元素项计数值需要加1;如果不含有,那么在共同前缀分支最后一个节点的子节点上构建新分支,新分支含有节点计数值是1。全部事务aj递归,直到FP-tree建立。 输电线路短路故障数据集合A中存在9个事务,当中:a1={b1,b2,b3,b4},a2={b2,b3,b4,b5},a3={b2,b3,b4},a4={b1,b2,b3,b4,b5,b6},a5={b1,b3,b6},a6={b2,b3,b6},a7={b1,b3,b4},a8={b1,b2,b3,b4,b7},a9={b1,b2,b4,b7}。 将最小支持度设成gmin=3,根据以上步骤建立FP-tree。图1中的头指针表中存在输电线路短路故障数据集的元素项和衍生次数,同时根据曲线连接FP-tree里全部相同元素项;直线相连节点描述父代和子带关系,父代至上[7]。 图1 FP-tree结构 1.1.3基于FP-tree挖掘频繁项集 为提升实际效率,先将Apriori算法与FP-tree结合使用,先进行Apriori算法挖掘,找出满足最小支持度的所有频繁项集,再将由频繁项集满足最小支持度和最小置信度要求的数据项相关联。Apriori算法主要集中在如何快速有效地找出满足最小支持度的所有频繁项集,Apriori算法需要多次重复地扫描数据,并产生大量的候选项目集来找出所有的频繁项集,因此,算法在时间和空间上的开销太大。为了克服这些不足,使用FP-tree进行挖掘。 频繁项集发掘的中心思想为递归挖掘,发掘每个元素项的条件模式基并建立条件FP-tree,在递归时发掘频繁项集[8]。设定条件模式基是基于某输电线路短路故障元素项为收尾的路径组合,路径中包括了此元素项和根节点间的全部子节点项。设定条件FP-tree是根据某元素项的条件模式基,是输入数据建立的FP-tree。详细流程如下: (1) 在FP-tree里得到输电线路短路故障某元素项的条件模式基。在头指针表某元素项bu指向的首个节点开始,遍历此元素项在FP-tree里具有连接关系的全部节点[9]。每逢一个输电线路短路故障检测节点,可实行依次上溯,同时记载此节点到根节点间存储的全部元素项,衍生一个前缀路径,将此前缀路径设值,此值与第一个节点元素项计数值相等。此元素项的剩下前缀路径集合属于输电线路短路故障条件模式基[10]。 (2) 通过输电线路短路故障条件模式基建立条件FP-tree。先构建输电线路短路故障的频繁项集列表,同时把bu导进频繁项集列表里,之后将根节点设成bu,将与bu相符的条件模式基设成输入数据,建立FP-tree,获取结果属于bu的条件FP-tree(条件FP-tree根节点从空集变成bu)。把条件FP-tree里的元素项(不包含根节点)依次放进输电线路短路故障的频繁项集列表里[11]。 (3) 递归发掘条件FP-tree里的频繁项。将条件FP-tree里输电线路短路故障每个元素项(不包含根节点)递归得到条件模式基,建立条件FP-tree,存储输电线路短路故障的频繁项,当FP-tree只具有一条分支便停止递归,获取最后的输电线路短路故障频繁项集列表,此列表存储具有bu的频繁项。 (4) 将头指针表里的元素项根据支持度实行升序分布[12],之后将各个元素项进行步骤(1)-步骤(3)处理,获取输电线路短路故障每个元素项的频繁项集,此项集即为频繁出现故障的输电线路,也称故障线路。 1.2.1故障行波传播过程 图2是故障线路模型。 图2 故障线路模型 故障出现方位存在三种状况: (1)c1、c2之间。 (2)c1、c2或者d1、d2之间。 (3)C、c2或者D、d2之间。 文章围绕故障点在两个监测点c1、d1之间实行分析。在C侧设定监测点c1、c2;基于D侧设定检测点d1、d2。C、D依次描述两端母线,c1、c2之间间隔是eC,d1、d2之间间隔是eC|D|。 若点d2至母线D的间隔是edD,点c1、d1至故障点g1间隔是ecg1、edg1,c1至母线C间隔是ecC,按照d1、d2检测的行波第一个波头,能够反演获取故障点的初始线模电流行波,其幅值设成LQ。 因为线模波速不小于零模波速[13-14],在研究行波第2个波头过程中,不分析首个行波的零模分量经过母线反射后抵达d1、d2的行波。这时d1、d2检测的线模电流行波第2个波头能够通过下述两种状况出现: (1) 首个行波通过母线C反射,然后通过故障点折射抵达d1、d2。 (2) 首个行波通过母线D反射,然后再传输至d1、d2。 假定ecC+eC+ecg1 如果间隔符合ecC+eC+ecg1 如果ecC+eC+ecg1>edD+ed,则将c1、c2与d1、d2互换,研究方法与上述一样。可建立目标函数,判断故障点的故障电阻和故障角情况,完成关键故障信息的详细分析。 1.2.2目标函数建立 综上所述,建立目标函数的原则是为了降低输电线路短路故障反演获取的行波幅值和理论运算的行波幅值差异。以Z相接地、MN相间短路、MN相接地短路为例,建立目标函数是: (1) (2) (3) 式中:V表示输电系统各项电压的最大值;φMN描述MN线电压故障初始角;φM、φN、φZ描述电压故障初始角;Wf描述故障电阻;i代表模量标号;LQi是按照d1、d2检测获取的第一个波头反演获取的故障点电流行波幅值;Lqi代表按照c1、c2检测获取的第2个波头正演获取的电流行波幅值;Lsi为根据d1、d2检测到的第2个波头正演求取的电流行波幅值;r为故障初始角;S0、S1、S2是经过反演参数运算获取的输电线路短路故障关键暂态信息波阻抗。则针对目标函数P(PZ、PMN、PMNH)来讲,只有故障电阻和故障初始角属于未知参量。所以,P表示相应的故障暂态信息。 实验使用21台服务器建立某电力公司输电线路短路故障的并行计算环境,分别模拟覆盖较广范围输电线路以及较长时间的输电线路。服务器的主频是2.41 GHz,操作系统是64位的Debian Linux。通过IBM DataGen[15]创造输电线路短路故障测试数据集,在当前模拟环境中,存在的项目总数是1 000种,各条记载的长度均值是10,随机选取数据参数进行仿真实验。 采用本文方法检测实验输电线路不同短路故障情况的关键暂态信息,测试本文方法的检测效果,结果如表1所示。 表1 不同故障情况下本文方法应用效果 续表1 根据表1数据显示,本文方法检测结果中故障角的误差最大值是0.79°,这时真实相角是91°;故障电阻的误差最大值是1.5 Ω,这时真实电阻是11 Ω。由此可知,本文方法的鲁棒性较优,在不同故障环境中均能够准确检测输电线路短路故障关键暂态信息。 为了进一步判断本文方法的应用性能,设定暂态信息种类依次是A:断路器操作、B:电容投切、C:单向短路、D:一次电弧、E:雷击。采用本文方法、基于行波反演的输电线路单相接地故障重演方法,以及基于奇异值分解理论的输电线路故障检测方法对五种故障关键暂态信息进行检测,三种方法对五种故障关键暂态信息的检测结果对比见表2。 表2 三种方法对五种故障关键暂态信息的检测结果对比 分析表2可知,三种方法对比之下,本文方法检测输电线路五种短路故障关键暂态信息时,对单向短路、一次电弧、雷击三种短路故障关键信息检测所耗费的时间最短,且与理论时刻相同,表明本文方法在检测输电线路短路不同故障关键暂态信息时的效率较快。 三种方法检测暂态信号的误差测试结果如表3所示。 根据表3数据可知,当需要检测的输电线路短路故障关键暂态信息是断路器操作和电容投切所导致时,本文方法的检测误差最小,仅有0.000 006,另外两种方法的检测误差均为0.000 013;而在剩余三种情况下,本文方法的检测误差仅有0.000 001,则本文方法检测精度最高。 设定海量输电线路短路故障信息,测试三种方法在大量故障数据检测结果,见图3。 图3 三种方法抗干扰性测试结果 根据图3可知,本文方法的检测数据量最大值高达0.97 GB,另外两种方法的检测数据量最大值依次是0.88 GB、0.86 GB。对比可知,本文方法的检测能力优于常规两种方法。 输电线路出现故障后的暂态行波属于一个具有突变型、奇异性的信号,准确检测输电线路短路故障关键暂态信息能够有效发掘输电线路短路故障问题。本文提出基于FP-growth算法的输电线路短路故障关键暂态信息检测方法,在不同故障环境中均能够准确检测输电线路短路故障关键暂态信息,且在检测输电线路短路故障信息时,本文方法的故障信息检测时间和故障节点数据量存在线性关系,具有较高的加速比;本文检测输电线路故障关键暂态信息时检测精度高,在增强电网供电可靠性、避免大停电事故方面具有重要意义。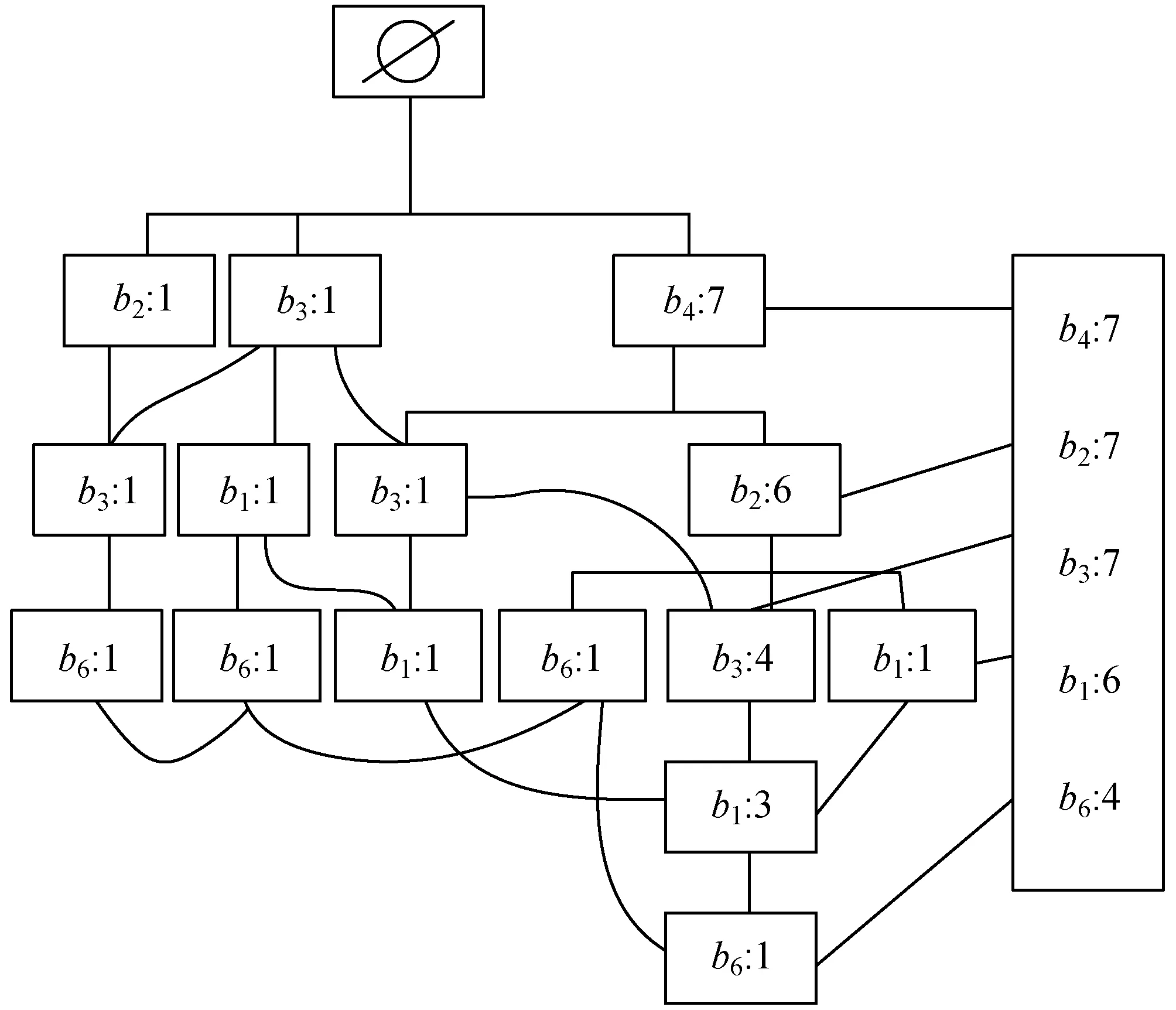
1.2 输电线路短路故障关键暂态信息提取
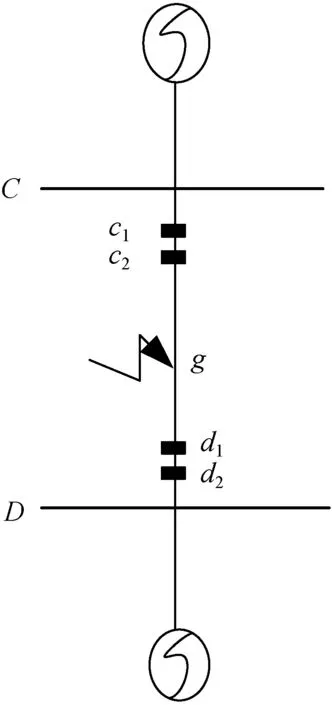


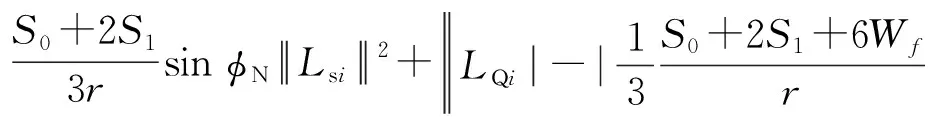
2 仿真实验分析
2.1 实验准备
2.2 多数据下设计方法实验结果与分析
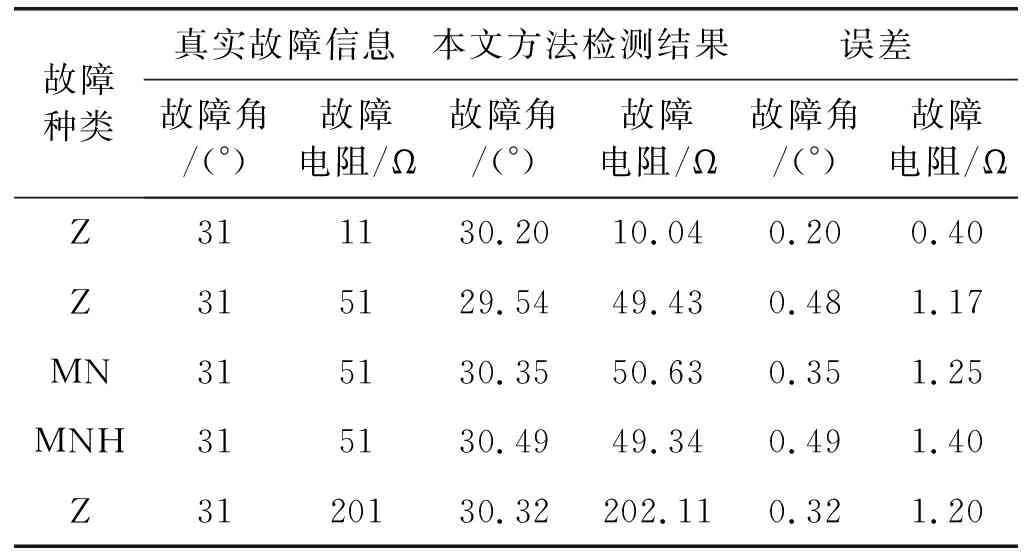
2.3 多检测状态下测试结果
2.4 误差测试
2.5 大量故障信息下测试结果
3 结 语
