恒力车削过程的模糊指数趋近律互补滑模控制

陈高华 张嫣然 李 悦

(太原科技大学电子信息工程学院 山西 太原 030024)

0 引 言

近年来，机械制造追求更加便捷、快速、高效的加工方式[1]。传统加工采用恒进给速度加工，为防止切削力过大损坏机床与刀具，只能选择较低的进给速度，导致加工时间长，加工精度低，无法满足新时代机械加工要求。而恒切削力加工，采用的是变进给速度加工，可以在切深较小时进行高速加工。恒力加工相较于传统的加工方式缩短了加工时间，提高了加工精度，延长了机床寿命[2]。

恒力切削对于加工过程实现快速化、高效化有重要作用，因此成为众多学者的研究对象。宋晓华[3]提出基于PID控制与模糊控制的切削加工过程双模控制，当偏差大时用模糊控制，偏差小时转由PID控制；张毅等[4]提出一种将预测控制与神经网络相结合的神经网络预测控制应用于恒力车削，使切削进给在切削深度发生突变前提前发生相应变化；余铭奇等[5]提出一种加工过程的模糊自适应PID的控制方法，运用模糊自适应PID控制方法，系统的调节时间缩短，响应速度加快，抗干扰能力和适应参数变化的能力要优于增益自适应的PID控制；陈首彦[6]提出采用模糊滑模控制应用与机器人切削，根据加工状态利用模糊规则调整滑模控制系数，进而改变进给速度，实现对机器人切削的切削力控制；Xu等[7]提出将前馈神经网络控制与自适应控制结合的控制方式，并且加工之前离线优化切削参数，该方法有好的稳定性和适用性；Zuperl等[8]提出将模糊控制与自适应控制相结合，实时修正模糊规则，实现在线调整进给速度，进而实现恒力切削；Liu等[9]建立了主轴电流与进给速度之间的数学模型，特别之处在于其检测并提取了主轴电流，将主轴电流作为反馈，所使用的控制方法是模糊控制与自适应控制相结合的方式。上述方法在恒力切削控制的研究方面取得了一定成果，但是在切深突变时切削力均出现了较大的超调，而采用滑模控制(Sliding Mode Control，SMC)可以很好地削减这一超调。加工过程具有很强的时变性、非线性、不确定性[10]。滑模控制作为一种鲁棒控制方法，对外部干扰和未建模动态具有完全的鲁棒性，因此对控制加工过程有其独特的优势，但滑模控制器存在输出抖振的缺陷，且无法消除，只能削弱。国内外众多学者就削弱滑模控制器输出抖振进行了大量研究[11-21]，其中包括采用改进现有的趋近律、非线性滑模面、观测器，以及与现有其他控制器结合或将几种方法混合使用等各种研究。

本文采用积分滑模面与互补滑模面结合的方法设计了互补滑模变结构控制器(Complementary Sliding Mode Controller，CSMC)，并将其与模糊控制结合，设计了一种用模糊控制策略实时整定指数趋近律指数系数的互补滑模控制器(Fuzzy Complementary Sliding Mode Control，F-CSMC)应用于恒力车削控制，并分别在切削深度台阶型变化与斜坡变化两种情况下进行了仿真研究。互补滑模控制中，采用积分滑模面与互补滑模面结合的方式，但其本质仍为线性滑模面，因此，兼具了积分滑模面与线性滑模面的优点，既削弱了抖振，提高了控制精度，又保持了滑模面降阶特性。在模糊控制中，通过模糊控制策略实时整定指数趋近律指数系数，降低切换控制的影响，可以在保证系统鲁棒性的同时削弱抖振。当运动点距离滑模面远时，加快收敛速度缩短收敛时间；当运动点到达滑模面附近时，减小趋近速度，有效地削弱传统滑模控制器的输出抖振。仅通过整定指数趋近律的一个参数指数系数就可以既实现缩短系统的收敛时间又削弱抖振，相较于同时整定两个参数节省了计算量。

1 车削过程建模

车削过程由伺服机构、机械传动和车削过程三个环节构成[22]，车削过程系统控制框图如图1所示，其中：Fn为给定切削力；F为检测切削力；e为误差；u为伺服电压；Vf为进给速度；f为进给量；Fs为实际切削力。

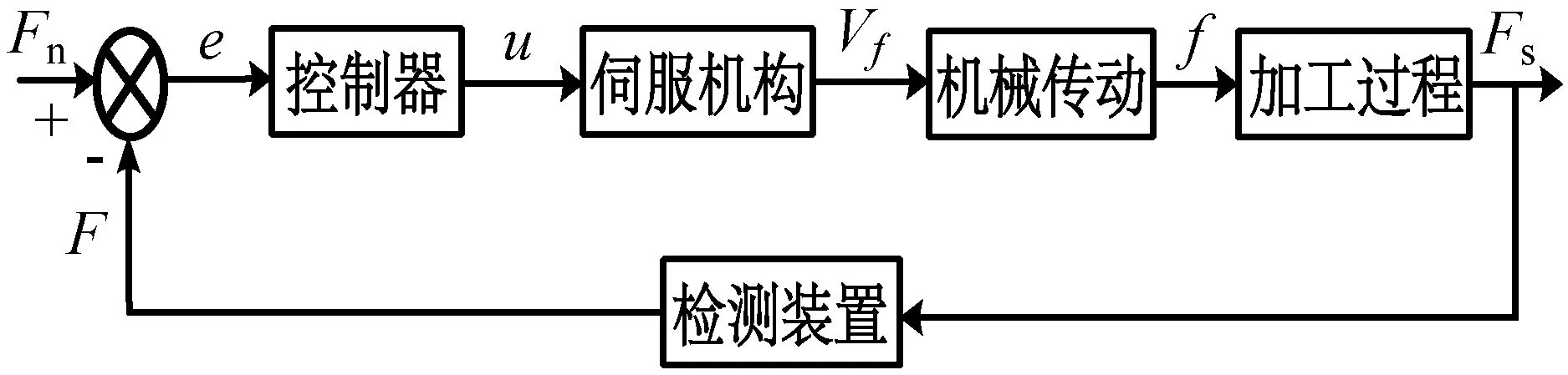
图1 车削过程系统控制框图

伺服机构可简化为一个二阶系统：

(1)

式中：Vf为进给速率；u为电枢电压；Km为伺服增益；ωn为伺服系统的自然频率；ξ为阻尼系数。

机械传动装置简化为进给量与进给速度之间的关系：

(2)

式中：p为刀具齿数，车削时为1；n为电机转速。

加工过程中进给量与切削力之间的关系可用切削力经验公式表示：

(3)

式中：Ks为切削系数，α与β是指数系数，三个系数均由大量实验后凭借经验给出；ap为切削深度，为本文的主动变化量。

因此，车削过程的传递函数为：

(4)

式中：Kd为测力仪转化系数。

2 互补滑模控制器设计

由式(4)可得到切削过程的微分方程：

(5)

取状态变量：

(6)

确定传统线性滑模面为：

(7)

式中：c为常数。

采用等效控制与切换控制共同作用的控制方式，其中等效控制保证滑动模态运动品质，切换控制保证系统运动点有限时间内到达滑模面，而利用指数趋近律既可以保证滑动模态到达阶段的动态品质，也可以削弱抖振[23]。传统线性滑模控制器输出uSMC为：

cx2-εcx1-εx2-Ksgn(s)]

(8)

式中：K为切换增益。

针对线性滑模控制，定义Lyapunov函数为V=s2/2。

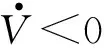
证明将指数趋近律公式代入Lyapunov函数中可得：

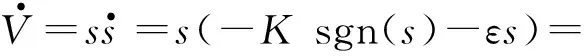
-K|s|-εs2=-(K|s|+εs2)

(9)

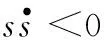
互补滑模控制器的滑模面采用积分滑模面与互补滑模面结合的方式。其中，积分滑模面定义为：

(10)

Bu+2λx2+λ2x1

(11)

定义广义滑模面为：

(12)

由于积分滑模面与广义滑模面存在同一参数λ，因此，可以得到它们的和为：

(13)

且积分滑模面与互补滑模面存在以下关系：

(14)

对互补滑模控制，定义Lyapunov函数为：

(15)

对Lyapunov函数求导并结合式(14)可得：

(16)

根据式(16)得到互补滑模控制器的输出：

(17)

ucsw=-Ksgn(Sg+Sc)-ε(Sg+Sc)

(18)

uCSMC=uceq+ucsw

(19)

并将式(17)-式(19)代入式(16)可得：

(Sg+Sc)[-Bucw-λ(Sg+Sc)]=

-λ(Sg+Sc)2-(Sg+Sc)·ρsgn(Sg+Sc)≤

-λ(Sg+Sc)2-|Sg+Sc|·ρ≤0

(20)

所构造的Lyapunov函数满足定理1，因此，所设计的互补滑模控制器可以使系统状态运动在有限时间内到达滑模面且系统稳定。互补滑模控制下，状态轨迹由滑模面外到达积分滑模面与互补滑模面的交线处，最终沿着交线到达原点。

3 趋近律参数ε整定

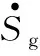
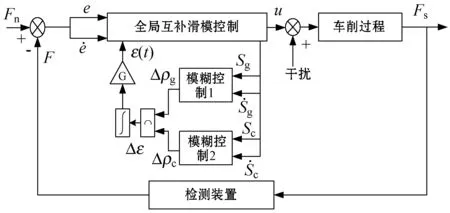
图2 模糊滑模控制器结构框图

模糊控制1与模糊控制2高度相似，其设计方法、隶属度函数及模糊规则也是相同的。定义模糊控制器的输入/输出模糊集均为{NB,NM,NS,Z,PS,PM,PB}，分别表示负大、负中、负小、零、正小、正中、正大。模糊控制的输入采用三角形隶属度函数，边界用S型隶属度函数，输入隶属度函数如图3所示；模糊控制的输出采用钟形隶属度函数，输出隶属度函数如图4所示。

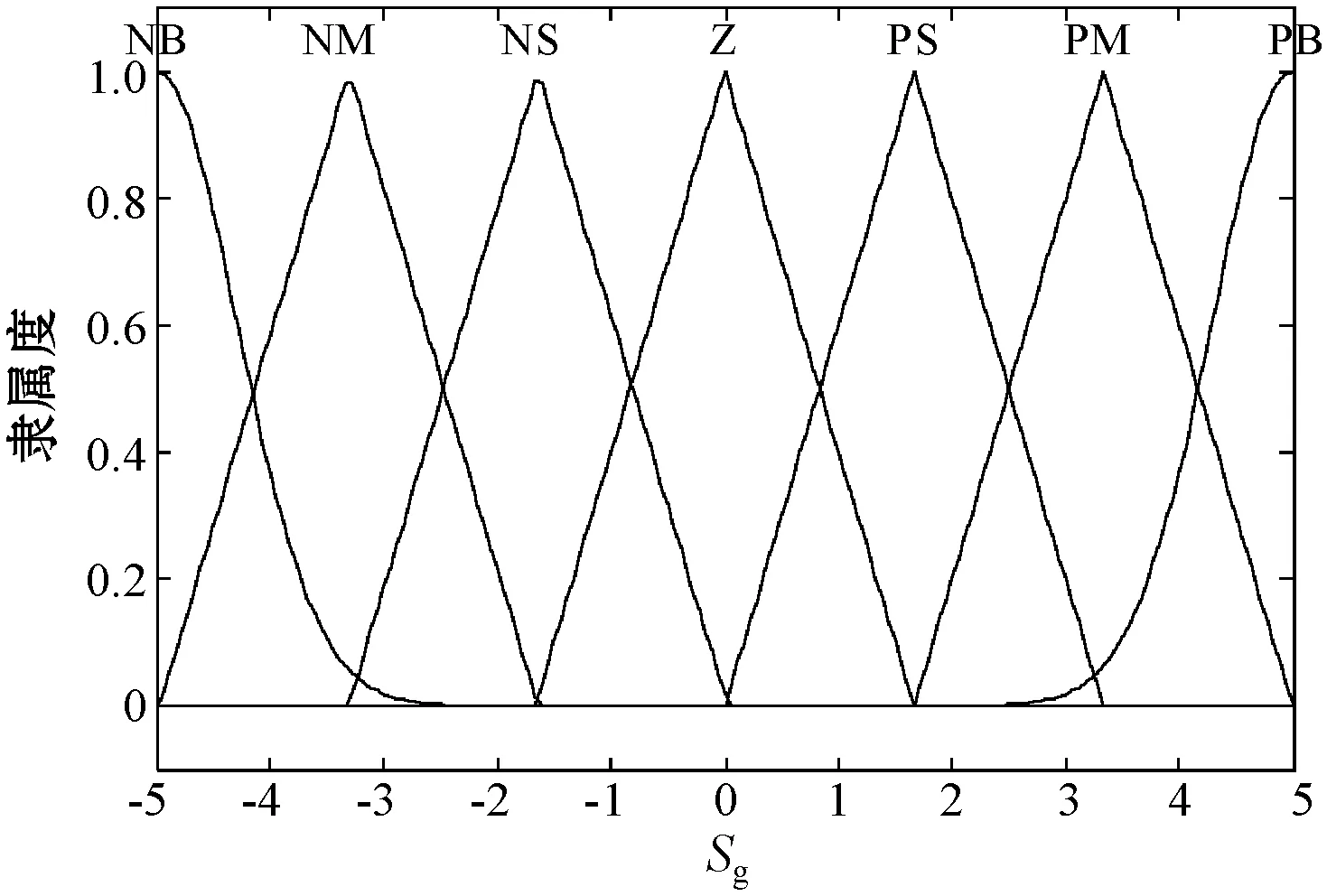
(a) 输入Sg/Sc隶属度函数

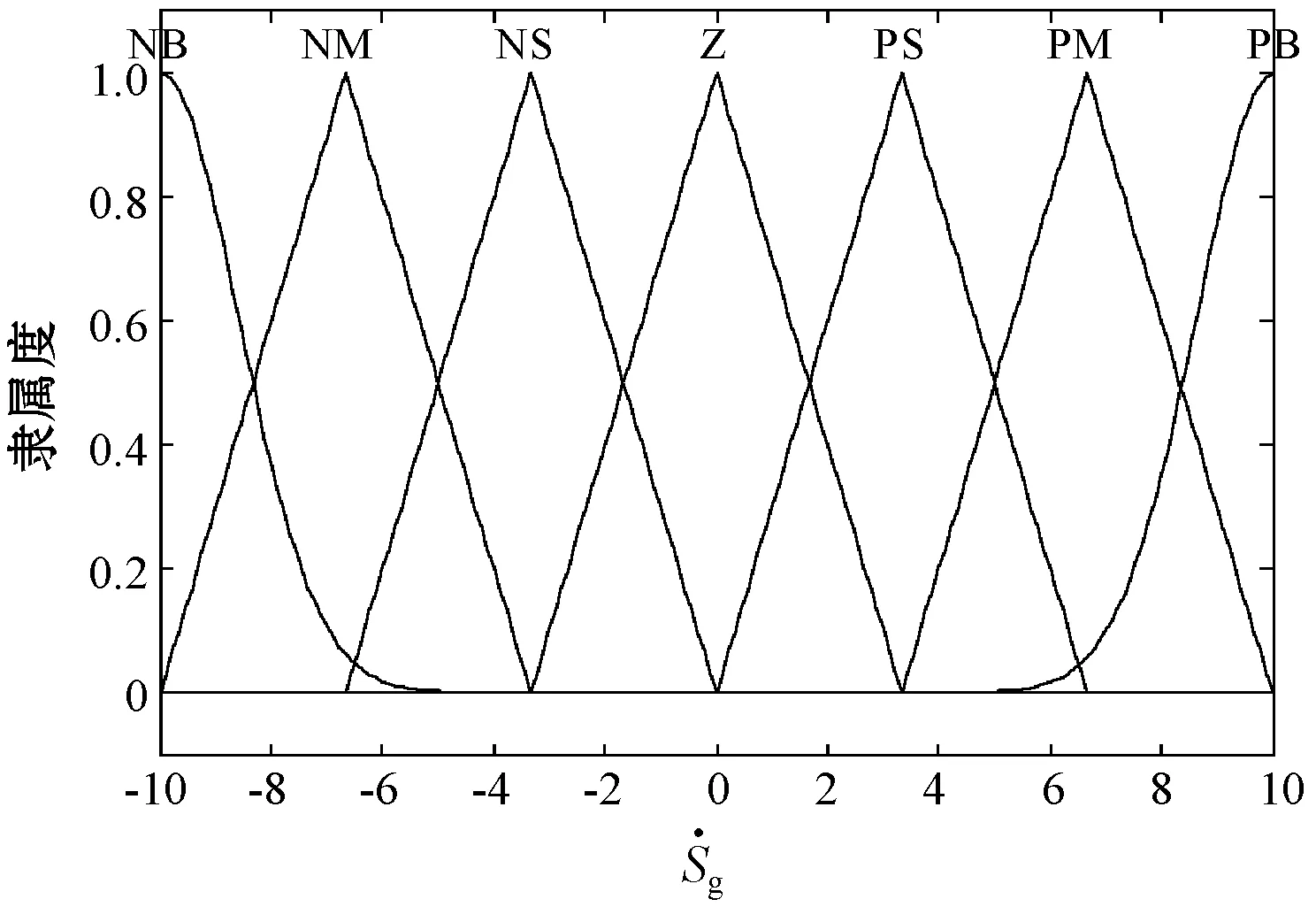
(b) 输入隶属度函数图3 输入隶属度函数

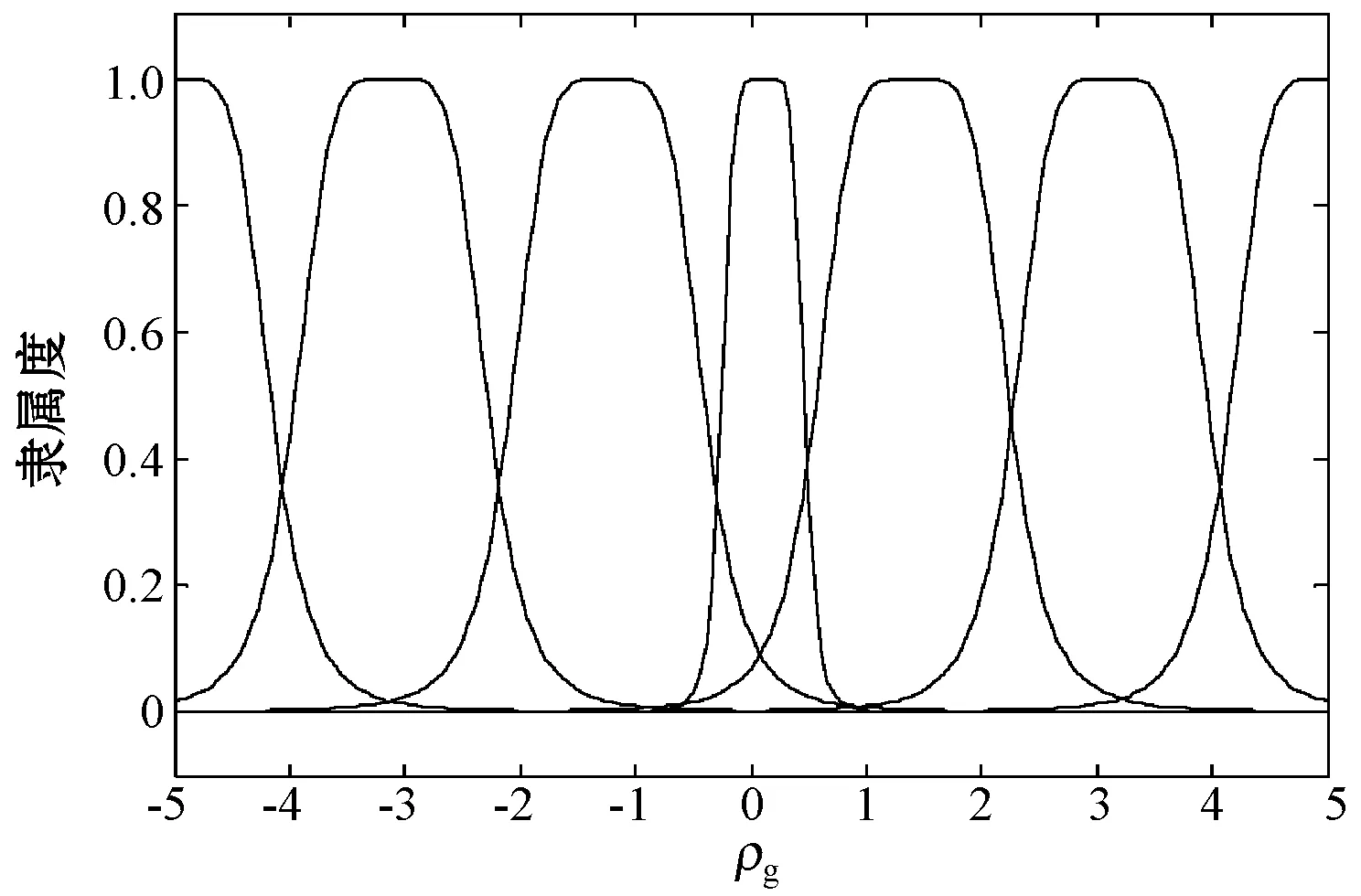
图4 输出Δρg、Δρc、Δε隶属度函数

所设计的模糊规则如表1所示。

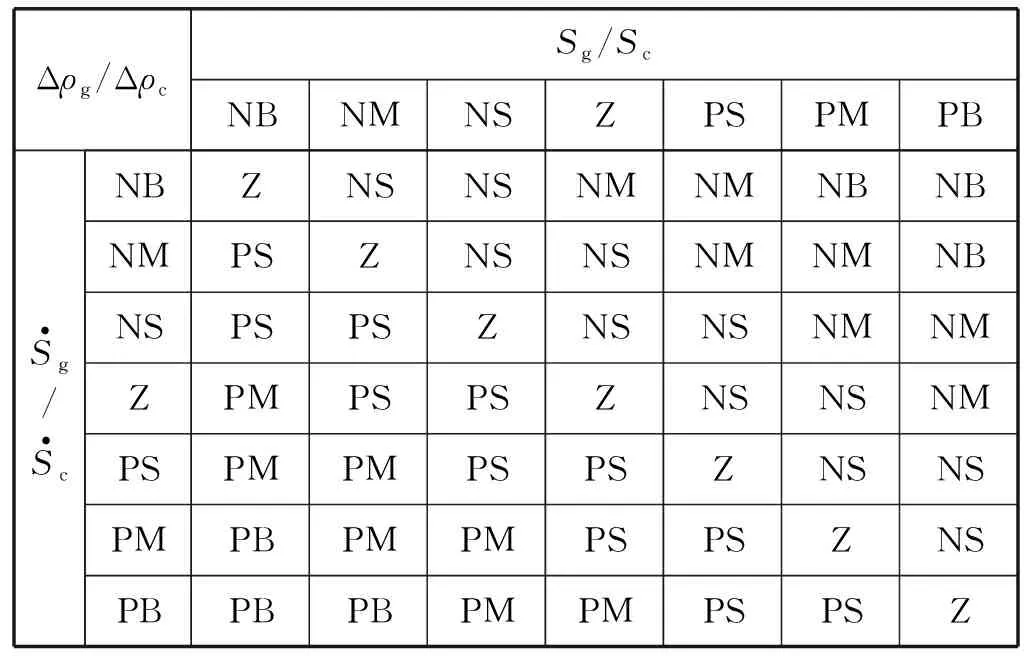
表1 模糊规则表

去模糊化采用重心法。对模糊控制1与模糊控制2的输出作“与”运算，得到模糊控制的最终输出：

Δρ=Δρg∩Δρc=min(Δρg,Δρc)

(21)

由模糊控制得到输出Δε，采用积分的方法对ε(t)的上界进行估计：

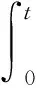
(22)

式中：G为不小于1的常数。

4 仿真与结果分析

设给定切削力为600 N，取车削过程模型的各项参数如表2所示。

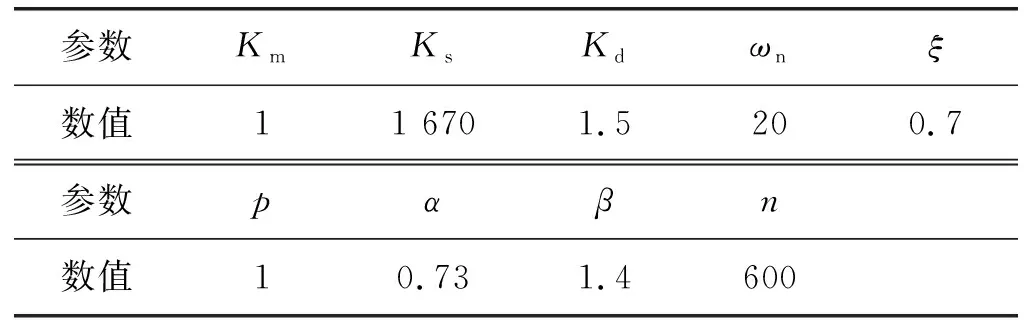
表2 车削过程模型的各项参数

将表1中的参数数值代入式(4)，得到车削加工过程的模型为：

(23)

为了验证本文方法的有效性，按照式(23)在MATLAB/Simulink中搭建车削过程模型，并分别在本文方法与指数趋近律参数固定的互补滑模控制方法、传统线性滑模控制方法及文献[26]采用的PID/PD复合控制进行比较。并在t=5 s时加入一个值为50的脉冲干扰，观察三种控制方法的抗干扰能力。

取指数趋近律参数固定的互补滑模控制器与传统线性滑模控制器的参数为c=25、λ=12.5、K=60、ε=5。本文方法模糊指数趋近律互补滑模控制器的参数为c=25、λ=12.5、K=60，ε由模糊控制方法在线整定。互补滑模控制与传统线性滑模控制按照式(8)与式(19)在Simulink中搭建仿真，模糊控制利用MATLAB中M文件嵌套进Simulink中进行参数整定。切深线性变化的情况下，在文献[26]采用的PID/PD复合控制方法下的切削力响应曲线如图5所示。传统线性滑模控制、互补滑模控制及模糊互补滑模控制下的切削力响应曲线如图6所示。

图5 切深线性变化时文献方法的切削力响应曲线

可以看出，当切深线性变化时，相较于文献[26]所用PID/PD复合控制方法，滑模控制方法的调节时间明显减小，抗干扰能力明显增强。由图6可看出本文方法的抗干扰能力、抖振大小、上升时间等指标均优于互补滑模控制方法和传统线性滑模控制方法。本文方法控制下的切削力响应曲线上升时间最短，抖振最小，抗干扰能力最强。

在切深每一秒发生一次突变的情况下，PID/PD复合控制方法下的切削力响应曲线如图7所示，传统线性滑模控制、互补滑模控制及模糊互补滑模控制下的切削力响应曲线如图8所示。

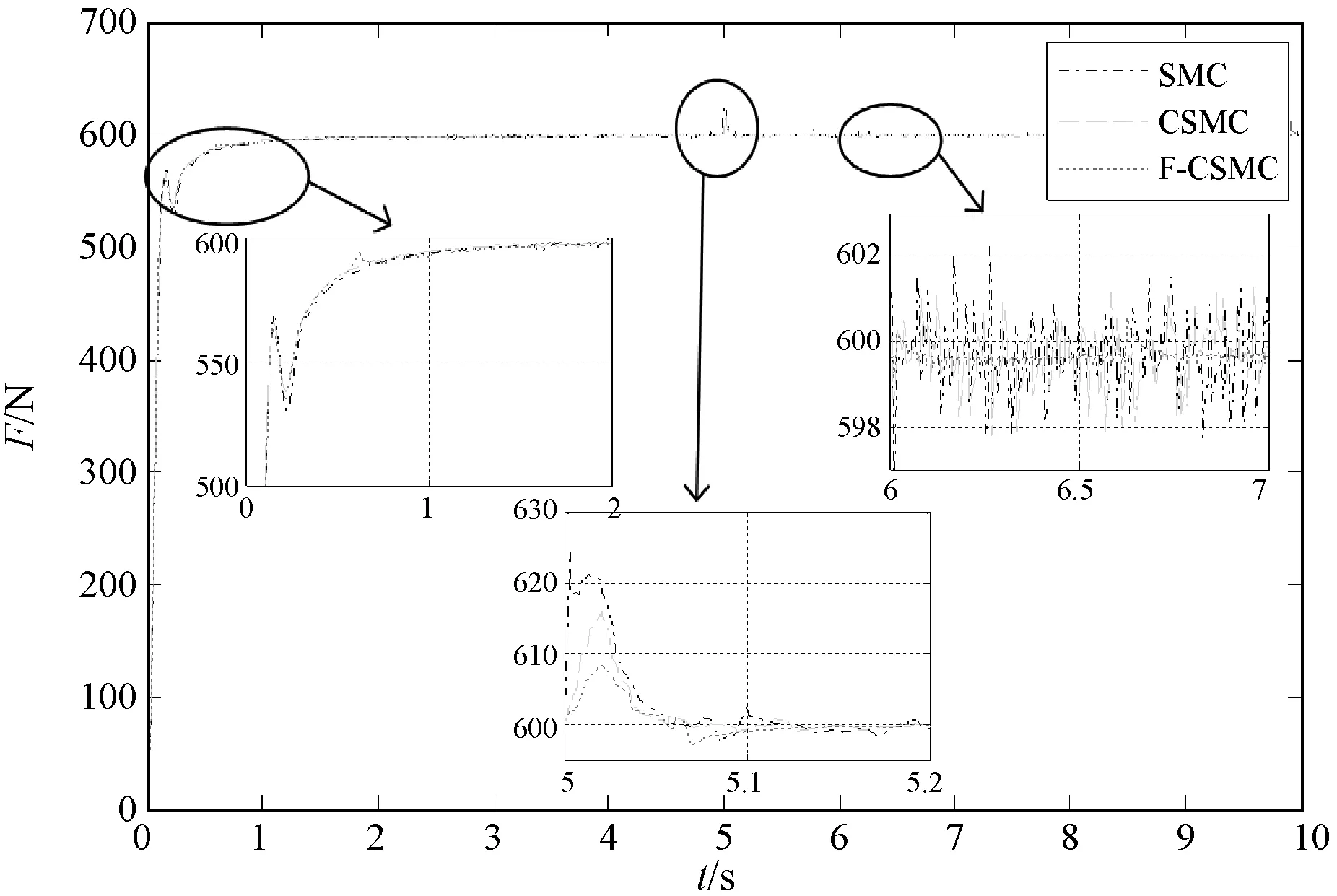
图6 切深线性变化时SMC、CSMC及F-CSMC下的切削力响应曲线

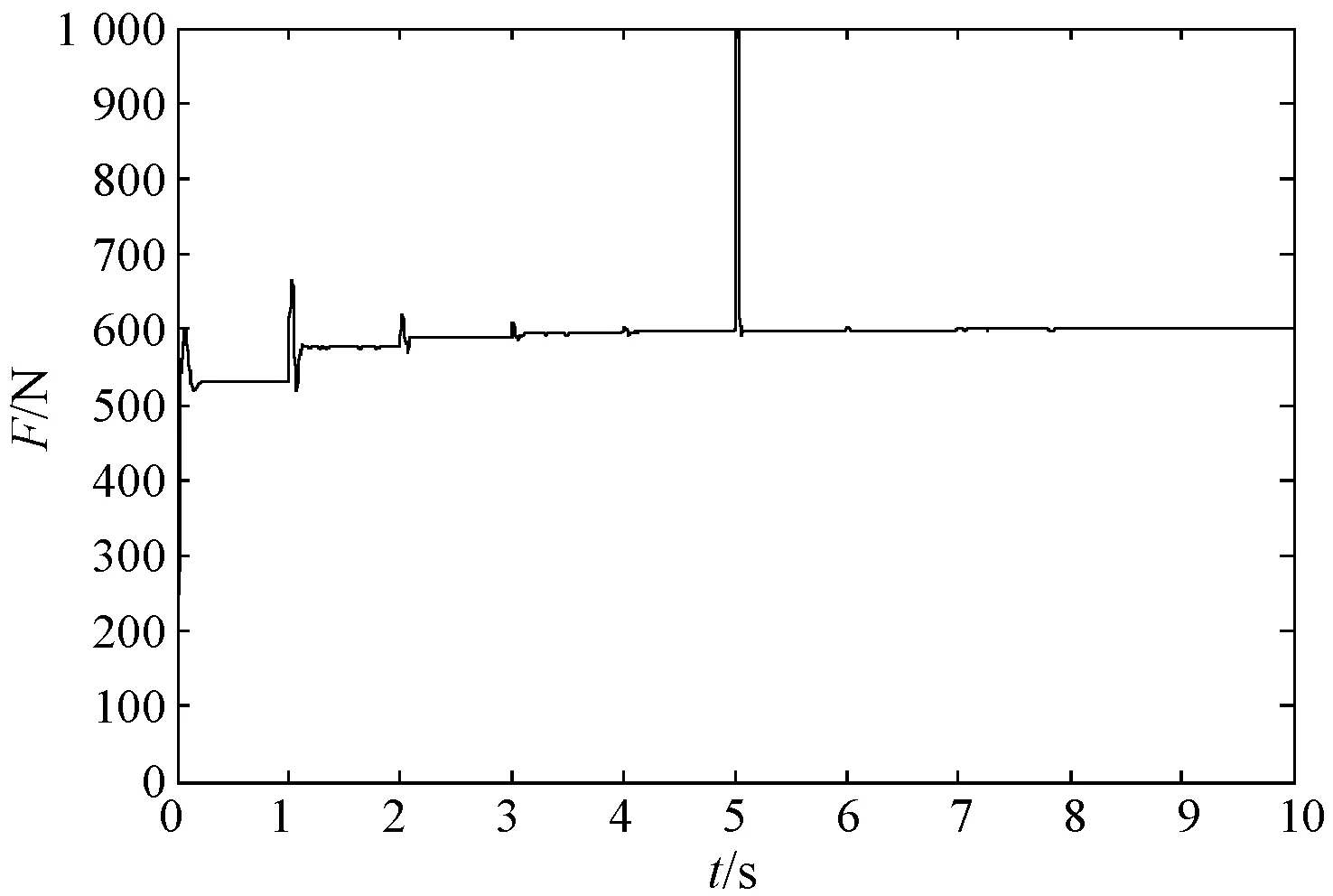
图7 切深突变时文献方法的切削力响应曲线

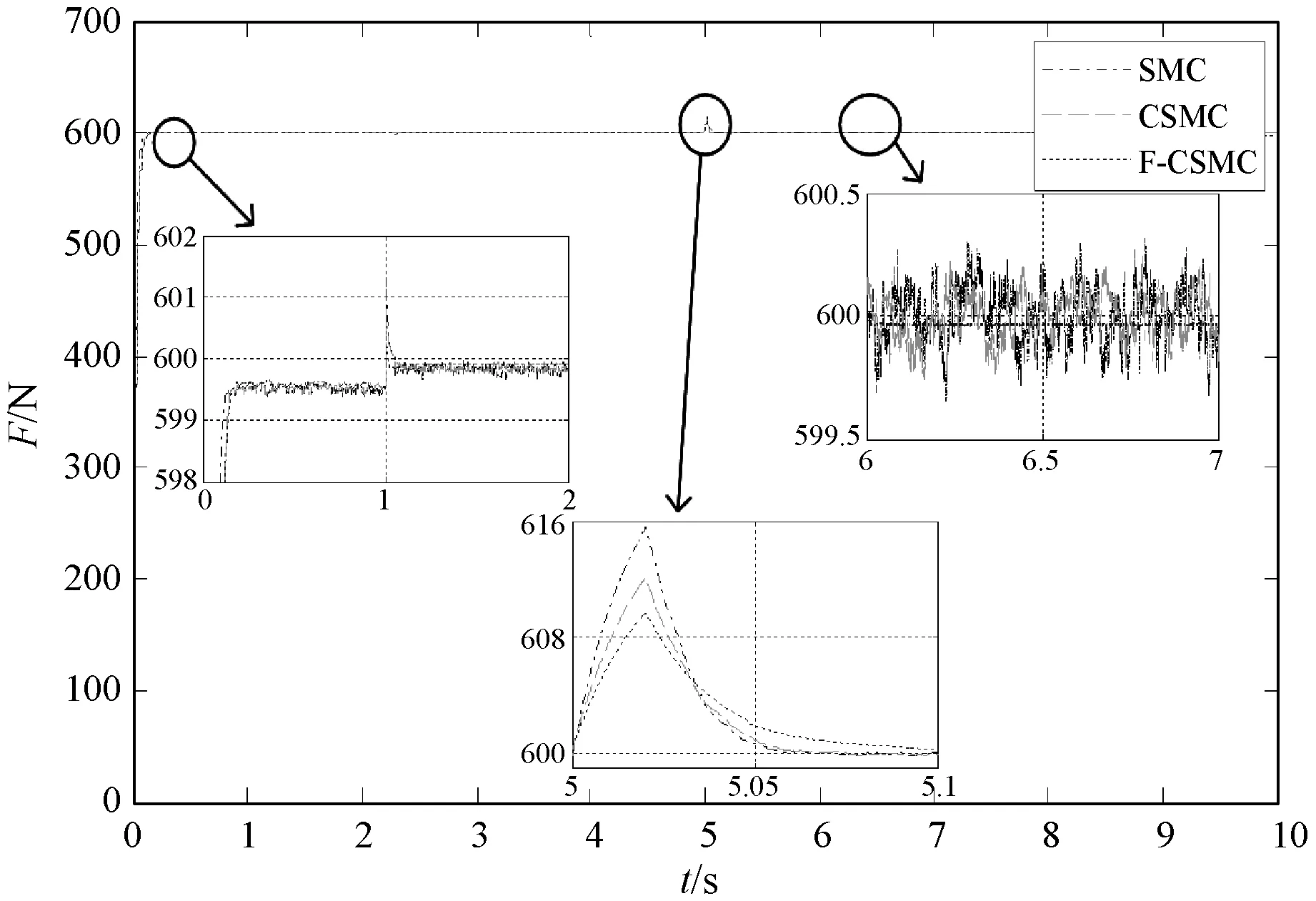
图8 切深突变时SMC、CSMC及F-CSMC下的切削力响应曲线

切深突变情况下，本文所提的车削过程的模糊指数趋近律互补滑模控制、趋近律参数ε恒定不变的指数趋近律互补滑模控制、传统线性滑模控制及PID/PD复合控制四种种控制方式的性能指标比较如表3所示。

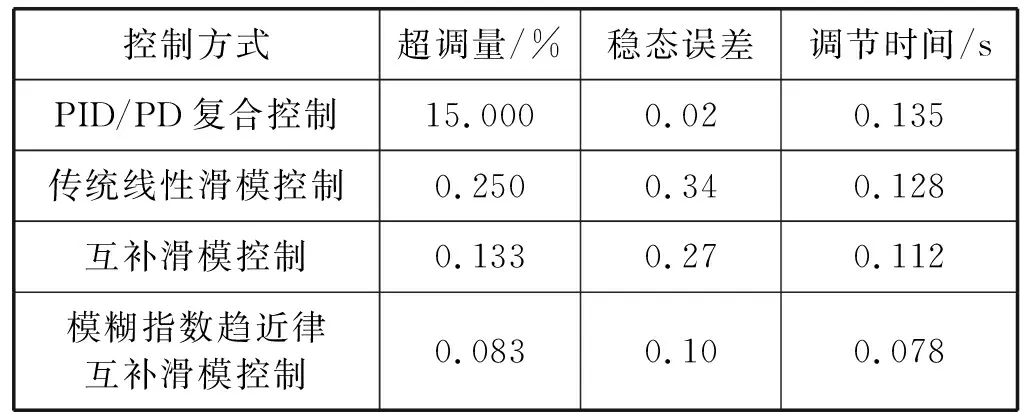
表3 四种控制方式下性能指标比较

可以看出，当切深突变时，文献[26]所采用的PID/PD复合控制方法超调大，对参数变化及扰动敏感。传统线性滑模控制方法与文献相比各性能指标有明显改善；互补滑模控制下切削力响应曲线的各项性能指标又进一步改善；本文方法与互补滑模控制方法相比，其超调更小，抗干扰能力更强，收敛速度更快且抖振幅度有所减少。

5 结 语

本文针对车削过程的恒切削力控制问题，以切深变化时仍能保证切削力恒定为目标，考虑到车削过程的非线性、时变性及不确定性，提出车削过程的模糊指数趋近律互补滑模控制方法。并分别在切深突变和线性变化两种情况下进行了仿真研究，结果表明，本文方法响应快、超调小，不仅一定程度上削弱了传统线性滑模控制器的输出抖振，而且增强了系统的鲁棒性，提高了控制精度。本文对于优化切削工艺，使切削过程更加高效、快速有重要意义。