帆船最小回转直径下风帆攻角研究

刘如磊 黄朝明 安云圣 刘绪儒 林叶锦

1(中国船舶工业系统工程研究院 北京 100094)2(集美大学轮机工程学院 福建 厦门 361021)3(大连海事大学轮机工程学院 辽宁 大连 116026)

0 引 言

回转性能是帆船一项重要性能，对帆船的适航性和航行安全性有重要影响。帆船回转性能不仅受船型和船舵参数(面积、剖面型线等)影响，还受风帆攻角操纵策略的影响。回转直径是帆船回转性能的重要因素，在定帆船情况下，研究风帆攻角操纵策略对帆船回转直径的影响具有较高的应用价值。

在风帆攻角对帆船回转直径的影响方面，国内外均未进行系统的研究。陈纪军[1]建立四自由度船舶操纵运动数学模型研究风帆攻角对船舶回转性能的影响；Masuyama等[2]基于风洞实验和水池实验结果，对古帆船不同舵深工况下抢风回转操纵进行了仿真研究；王建华等[3]借助风压模拟装置实现静水中模拟有风时风帆助航船舶回转性实验；孙烨等[4]基于CFD数值模拟方法研究舵角与帆船运动作用关系，通过响应型分离模型模拟帆船Z字形航行分析帆船回转性能。以上研究虽然探究了风帆对船舶回转性能会产生影响，但均未给出风帆攻角操纵策略。

风帆空气动力作用点与船体的受力作用点不在同一垂线上，风帆作用力产生的转首力矩对帆船回转有影响。当船舵产生的转首力矩与风帆产生的转首力矩方向一致时，帆船回转直径减小；当船舵产生的转首力矩与风帆产生的转首力矩方向相反时，帆船回转直径增大。

本文忽略转舵速度对帆船回转性能的影响，综合考虑风帆和船舵对帆船回转共同作用的影响，在静水、理想风况下对帆船的最小回转直径的风帆攻角操纵策略进行研究，探究风帆作用力对帆船回转性能的辅助作用。

1 帆船运动数学模型

1.1 目标帆船参数与运动坐标系定义

本文以自主设计双体帆船为目标船进行研究，其主要参数如表1所示。

帆船海上航行包括前进、横移、垂荡、艏摇、横摇和纵摇六个自由度。在合理范围内简化分析假设目标帆船为刚体，双体帆船稳心足够大，忽略横摇和纵摇对帆船回转性能的影响，低速航行下不考虑兴波影响，本文仅研究水平面上的帆船运动，因此仅考虑前进、横移和横摇三个自由度运动[5]。

建立随船坐标系xoy和全局坐标系x0o0y0，如图1所示，随船坐标系的原点o与帆船重心重合。其中：u为船舶前进速度；v为横移速度；r为首摇角速度；u与v的合速度为帆船航速Vs；船首方向ox与帆船航速Vs的夹角β为船舶漂角；船首方向ox与全局坐标系o0x0的夹角ψ为船舶首向角；δ为船舶舵角；Vt为绝对风速；θt为绝对风向角；Va为船舶相对风速；θ为船舶相对风向角。

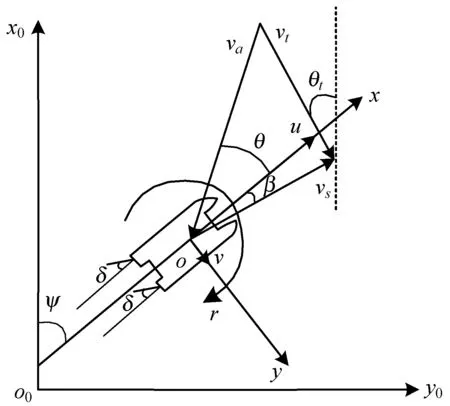
图1 帆船运动坐标系

1.2 三自由度帆船运动数学模型

基于响应型船舶操纵分离(MMG)方法建立三自由度帆船运动模型[6]：

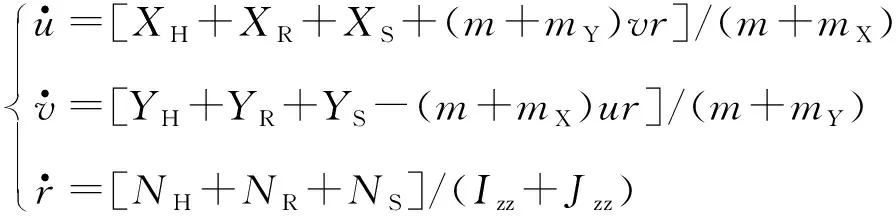
(1)

式中：m为船舶总重量；Izz为随船坐标系下帆船对z轴的转动惯量；Jzz为随船坐标系下帆船对z轴的附加转动惯量；mX和mY分别为随船坐标系下在前进方向和横移方向上的附加质量；XH、YH、NH为裸船阻力和阻力矩；XR、YR、NR为船舵作用力和力矩；XS、YS、NS为风帆助推力、风帆侧推力和风帆转首力矩。

帆船的船体水动力数学模型计算参考文献[6]对帆船进行受力分析和建模。

1.3 船舵受力

船舵受力是基于船舵水动力特性理论，通过舵叶升阻力曲线求得，对应关系为[7]：

(2)

式中：CXδ、CYδ、CNδ为舵叶助推力系数、侧推力系数和偏航力矩系数；LR、DR为舵叶的展长和弦长；αR=δ+β为船舵攻角；ρ为海水密度，取1 025 kg/m3。

1.4 风帆受力

帆船动力是基于风帆空气动力特性理论，风帆受到空气动力对应关系为[8]：

(3)

式中：CX、CY为风帆助推力系数和侧推力系数；ρa为空气密度；va为相对风速；SW为风帆的侧向投影面积；er为风帆动力作用点与船体的作用点垂线距离，取0.2 m。

2 风帆作用力对帆船回转直径的影响

2.1 风帆攻角方向分析

基于风帆空气动力特性理论，即空气流体流过风帆表面时，风帆会产生沿气流方向的阻力和垂直于来流方向的升力。采用无量纲化成升力系数和阻力系数表示，对应关系为：

(4)

式中：FL和FD为风帆升力和阻力；CL和CD为风帆升力系数和阻力系数。低速空气流体视为不可压缩流体，根据风帆空气动力特性理论，CL和CD仅与风帆攻角α有关，且存在一一对应关系。

本文选用风帆无公开的升阻力系数，采用CFD技术对稳态下目标风帆空气动力性能进行数值模拟。目标风帆的升阻力系数随攻角的对应关系如图2所示。

图2 风帆作用力系数随攻角变化曲线

对风帆升力和阻力进行合成分解，得到沿帆船首向的风帆助推力和垂直于首向的风帆侧推力。风帆攻角沿着相对风向角逆时针旋转为正，受力情况如图3所示，对应关系见式(5)。

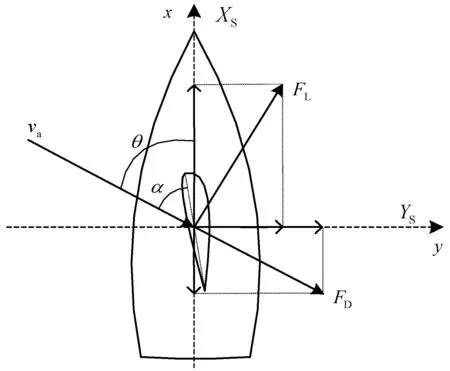
图3 攻角为正时风帆受力示意图

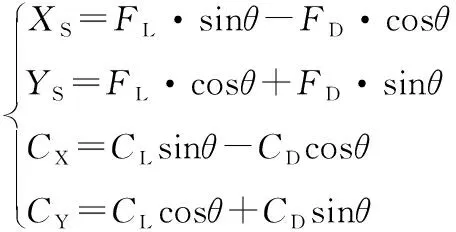
(5)

风帆攻角沿着相对风向角顺时针旋转为负，受力情况如图4所示，对应关系见式(6)。

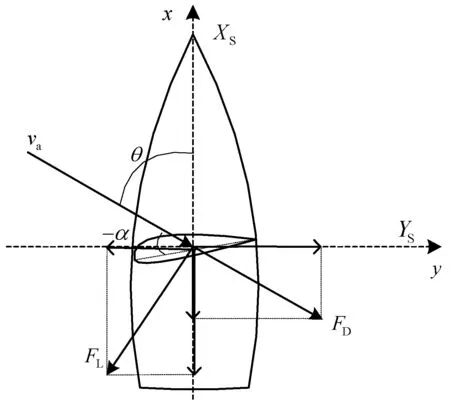
图4 攻角为负时风帆受力示意图

(6)

2.2 帆船回转方向分析

欲使风帆辅助船舵回转，则风帆转首力矩与船舵转首力矩方向相同，效果叠加。

当帆船向右回转时，向右转舵，则需风帆侧推力指向帆船右舷，风帆助推力指向帆船船首。结合图2和式(5)、式(6)，相对风向角在0°～90°范围内，风帆攻角为正，可达到辅助回转效果；相对风向角在95°～180°范围内，无论风帆攻角正负均可实现辅助回转效果；相对风向角在185°～270°范围内，风帆攻角为负，可达到助推效果；相对风向角在275°～360°范围内，无论风帆攻角为正或者负均无法达到助推效果。

当帆船向左回转时，向左转舵，则需风帆侧推力指向帆船左舷，风帆助推力指向帆船船首。结合图2和式(5)、式(6)，相对风向角在0°～90°范围内，无论风帆为正或者负，均无法达到辅助回转效果。相对风向角在95°～180°范围内，风帆攻角为正，可达到辅助回转效果；相对风向角在185°～270°范围内，无论风帆攻角正负均可实现辅助回转效果；相对风向角在275°～360°范围内，风帆攻角为负，可达到辅助回转效果。

综上，对帆船不同方向回转的辅助效果，在不同相对风向角选择风帆攻角旋转方向不同。在无论风帆攻角为正负均可达到辅助回转效果的相对风向角范围内，分析最优辅助回转的风帆攻角。为更准确获得帆船不同回转方向下最佳辅助回转效果，需计算不同相对风向角下对应的风帆攻角。

3 风帆攻角策略分析

3.1 帆船运动仿真模型

基于上文帆船运动数学模型结合目标船参数，采用MATLAB/Simulink建立目标船运动仿真模型，如图5所示。

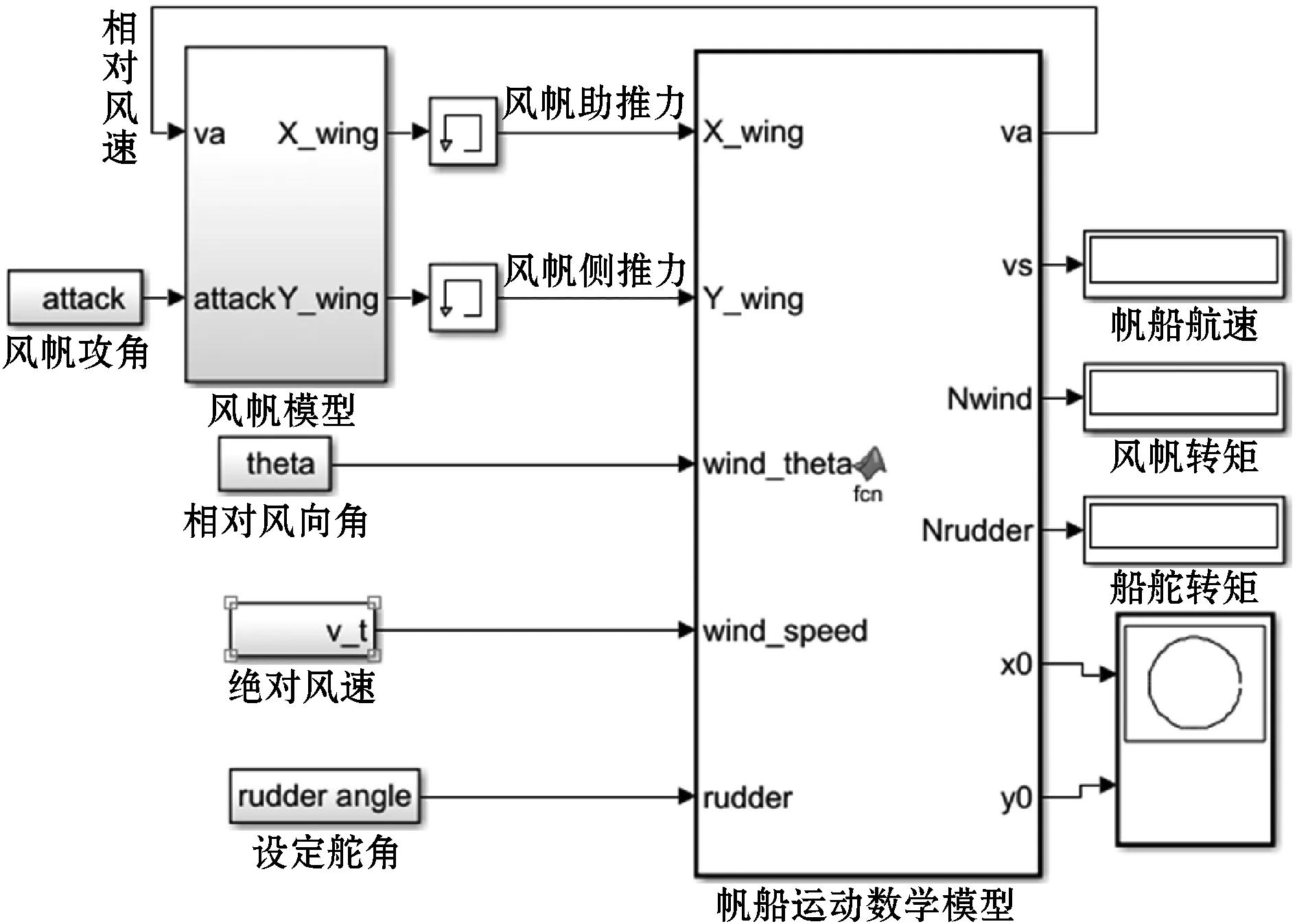
图5 帆船运动仿真模型

模型输入包括相对风向角、绝对风速、风帆攻角和设定舵角，输出为帆船航行轨迹参数、帆船航速、风帆转矩和船舵偏航力矩。为得到不同相对风向角下风帆攻角策略，将相对风向角和风帆攻角作为系统输入，经过帆船运动模型计算得到相对风速，输出给风帆模型，再将其计算得到的风帆作用力输出给帆船运动模型。设定舵角为±35°，绝对风速为8 m/s，变相对风向角、风帆攻角输入帆船运动模型，输出的帆船回转直径和帆船航速作为研究风帆攻角策略的依据。

3.2 仿真实验及结果分析

按照设定的参数进行仿真计算，分别从向左回转和向右回转两方面进行研究。相对风向角在0°～360°范围内，取5°为相对风向角间隔，风帆攻角在0°～90°范围内，取3°为风帆攻角间隔，获得变相对风向角工况下帆船回转直径随风帆攻角变化曲线簇。

3.2.1帆船向右回转

当帆船向右回转时，设定舵角为+35°，将0°～360°相对风向角和0°～90°风帆攻角输入帆船仿真模型，计算每个相对风向角工况对应的帆船回转直径随风帆攻角变化曲线。将相对风向角分为0°～90°、95°～180°、185°～265°和275°～360°四组。

在相对风向角0°～90°范围内，根据2.2节分析结果，对正风帆攻角进行研究。以相对风向角85°为例，帆船运动参数随风帆攻角变化曲线如图6所示。

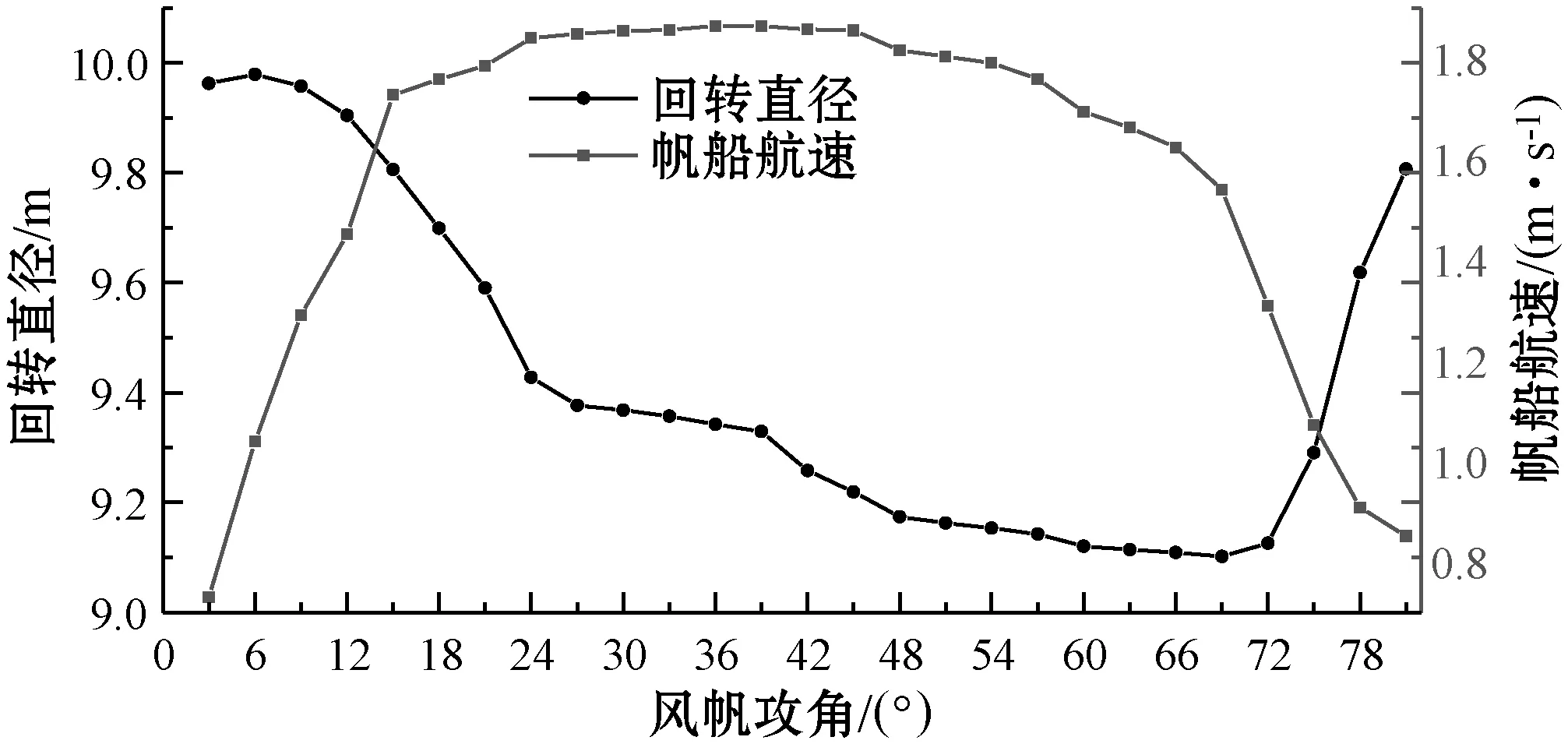
图6 相对风向角85°时帆船参数随攻角变化

可以看出，风帆攻角在3°～69°范围内，帆船回转直径与风帆攻角呈正相关，在69°～81°范围内，帆船回转直径与风帆攻角呈负相关，在81°～90°范围内，帆船助推力与船首方向相反，所以无法航行，无有效输出。欲达到最小回转直径，则选择最小回转直径对应的风帆攻角。在相对风向角85°时，风帆攻角69°对应回转直径最小，并且帆船航速大于1 m/s，最终选择风帆攻角为69°。

在相对风向角95°～180°范围内，根据2.2节分析结果，对不同方向攻角进行研究。以相对风向角140°为例，输出帆船回转直径随风帆攻角变化曲线如图7所示。

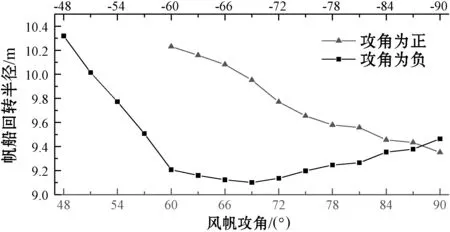
图7 相对风向角140°时，回转直径随不同方向攻角变化曲线

可以看出，当相对风向角为140°时，在小攻角范围，形成的力矩相反，无辅助回转效果。风帆攻角(±代表方向)在60°～90°范围内，风帆攻角为正时，帆船回转直径与风帆攻角呈负相关；风帆攻角在48°～90°范围内，帆船回转直径随风帆攻角先减小再增加。所以选择风帆攻角为-69°。

在相对风向角185°～270°范围内，根据2.2节分析结果，对负风帆攻角进行研究。以相对风向角190°为例，输出帆船回转直径随风帆攻角变化曲线如图8所示。

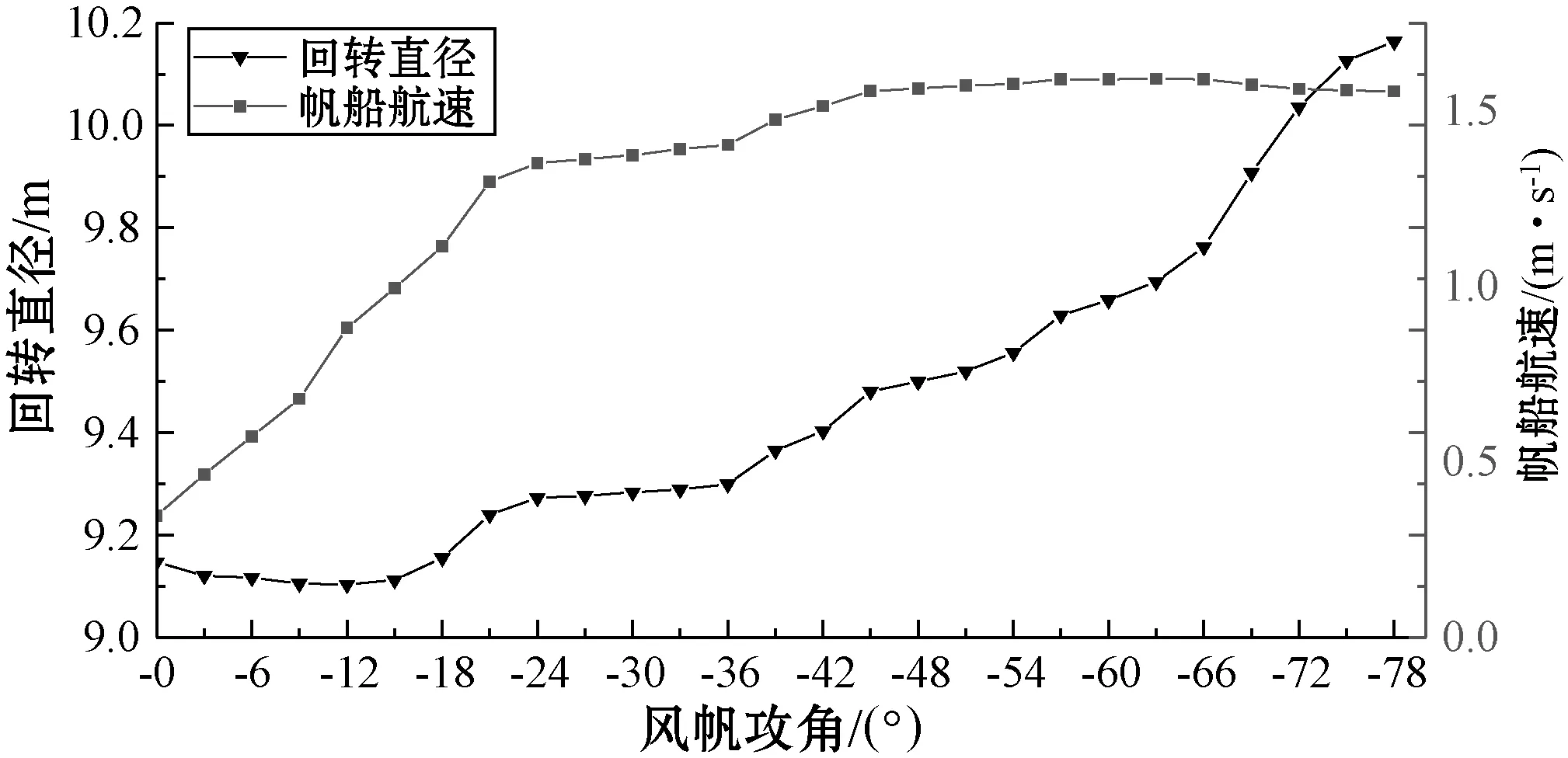
图8 相对风向角185°时帆船参数随攻角变化

可以看出，在小攻角范围内，帆船回转直径随攻角的增大而减小，风帆攻角在大于12°范围内，帆船回转直径会随风帆攻角的增大而增大。在相对风向角190°时，风帆攻角-12°对应回转直径最小，并且帆船航速大于1 m/s，最终选择风帆攻角为-12°。

当相对风向角在275°～360°范围内，风帆无法达到辅助回转效果，则使风帆对帆船回转直径影响尽可能小，因此选择风帆攻角为0°。

按照以上四组相对风向角的分析方法，计算变相对风向角下，帆船回转直径随风帆攻角的变化曲线，拟合成图9。

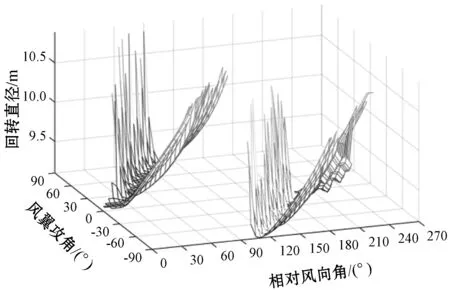
图9 不同相对风向角下帆船向右回转直径随攻角变化曲线

3.2.2帆船向左回转

当帆船向左回转时，设定舵角为-35°，分析方法与帆船向右回转相同，将0°～360°相对风向角和0°～90°风帆攻角输入帆船仿真模型，计算每个相对风向角工况对应的帆船回转直径随风帆攻角变化曲线。将相对风向角分为0°～90°、95°～180°、185°～265°和275°～360°四组，计算变相对风向角下，帆船回转直径随风帆攻角的变化曲线，拟合成图10。

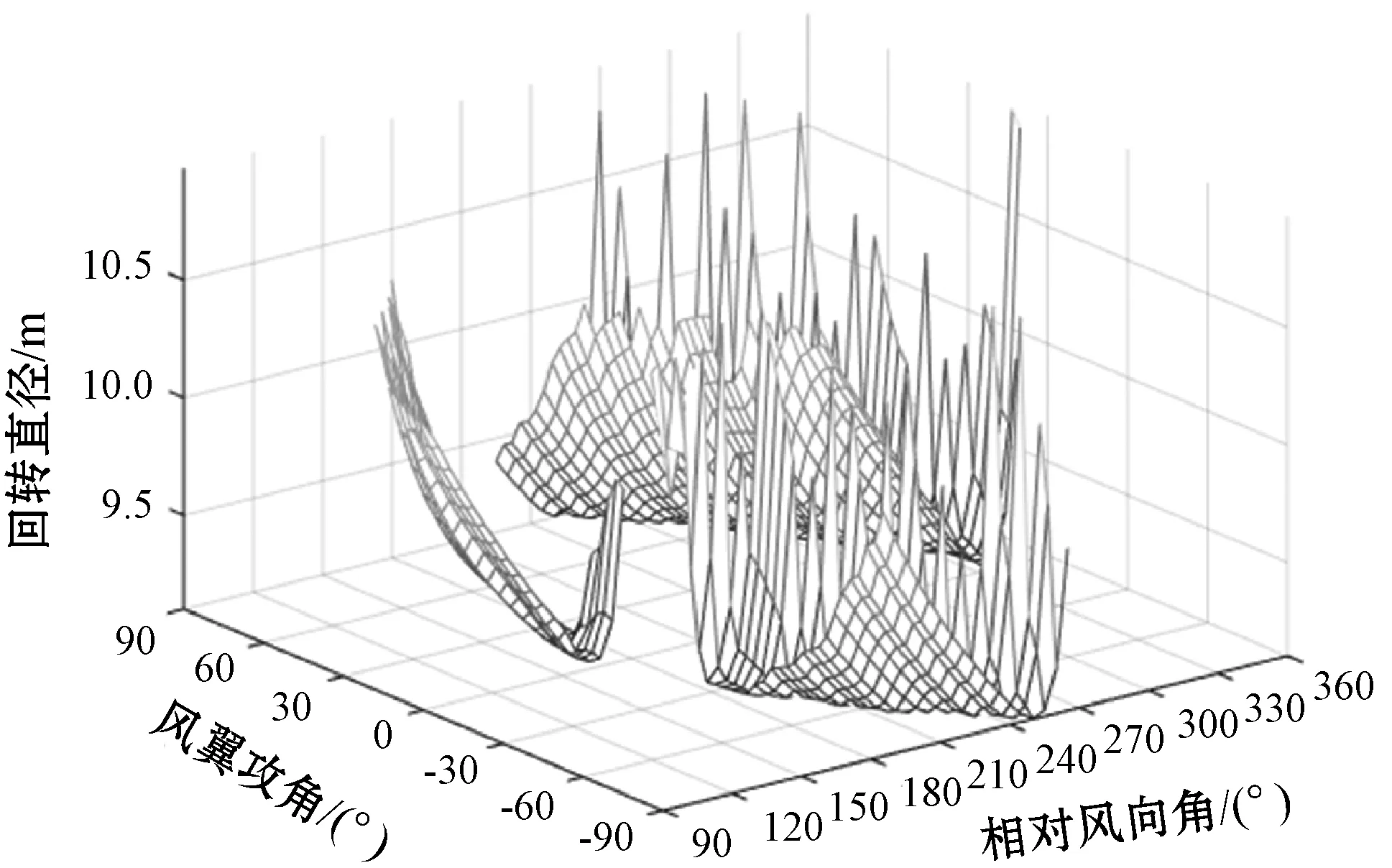
图10 不同相对风向角下帆船向左回转直径随攻角变化曲线

3.2.3风帆最佳攻角策略

综上，以最小帆船回转直径为评价标准，选取图9、图10上最佳风帆攻角操纵策略。获得最小帆船回转直径下，帆船向右、向左回转时，不同相对风向角下最佳风帆攻角操纵策略曲线如图11所示。

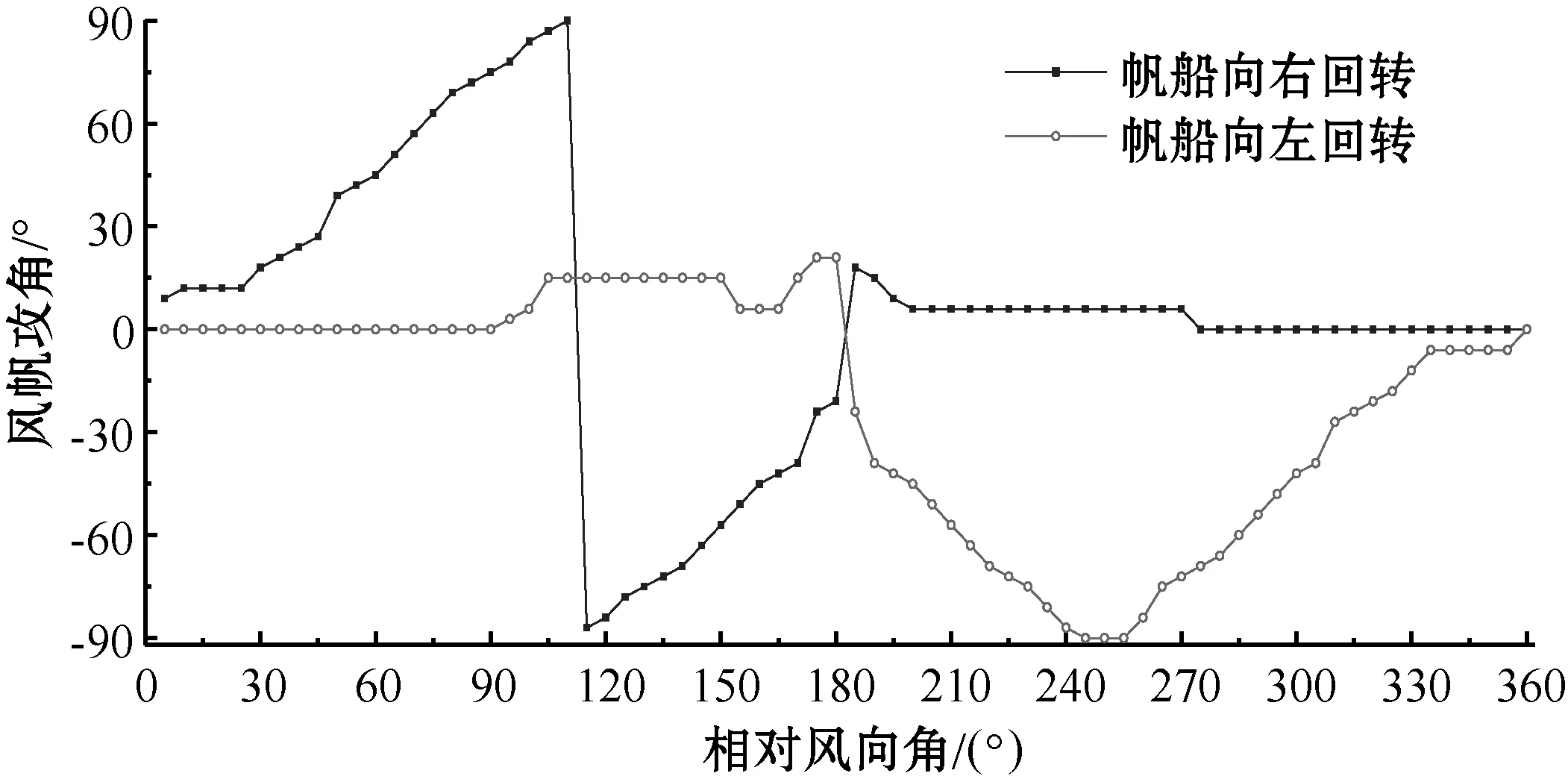
图11 最小回转直径下风帆攻角随相对风向角控制策略

3.3 实验验证

本文实验使用的测试平台如图12所示。

图12 帆船验证测试

无人帆船使用高性能MCU控制，采用风速风向传感器、AHRS九轴姿态传感器、无线串口通信，转帆和转舵采用大扭矩磁编码舵机控制。帆船航行的位置、姿态信息可以实时发送到岸端电脑控制端。验证实验分为向左回转和向右回转，分别采用传统的风帆最大助推力控制策略和最小回转直径下的风帆攻角控制策略进行对比测试。先进行帆船定航向航行，当航速达到0.8 m/s时进行回转测试，舵角为±35°，无人帆船部分实验航行轨迹如图13所示，回转实验结果如表2所示。

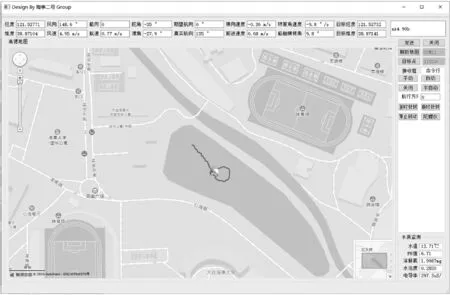
图13 向左回转，最小回转直径控制风帆策略航行轨迹

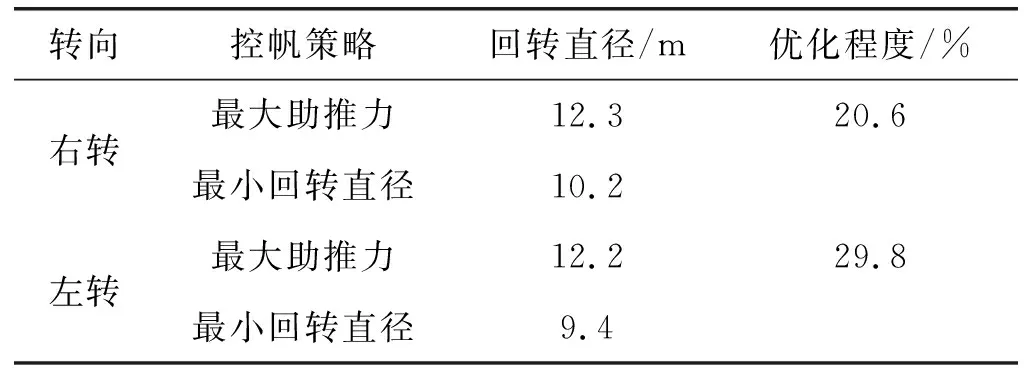
表2 帆船测试结果表

4 结 语

针对帆船回转性能的研究，本文综合考虑风帆和船舵对帆船回转性能的共同影响，对风帆攻角控制策略进行研究，获得了目标帆船最小回转直径下的风帆攻角策略。本文所做的工作对帆船海上安全航行，对帆船的转向等动作有重要意义，对无人帆船智能航行风帆攻角控制器的设计提供理论参考。结合目标帆船运动仿真模型，对相同相对风向角下能为目标帆船提供最小回转直径的风帆攻角进行分析和归纳，可以得出以下结论：

(1) 帆船回转直径大小与帆船稳态航速有关，与初始航速无关。

(2) 风帆攻角策略是帆船回转性能的重要影响因素。与目前常用的帆船航行最大助推力风帆攻角策略相比，最小回转直径控制风帆攻角策略帆船回转直径可减小20%，回转性能提升显著。

(3) 风帆攻角策略分别从向左、向右回转方向和正负风帆攻角分析验证，得出本文制定最小回转直径控制的最佳风帆攻角策略。