基于蚁群算法的打击链方案推荐研究*

罗云枫 张 剑

（武汉数字工程研究所 武汉 430205）

1 引言

在信息技术的推动下，使传统的战争理念发生变革，战争面貌也随之一新，催生了以信息作战为主导的信息化战争的到来。这促使我们改变传统的作战模式，构建以网络战、信息武器为特点的信息作战打击链。

其中，在多条打击链中选择最适合当前情况的打击链方案显得尤为重要，这也会直接影响到当前的作战策略。要想在繁多的打击链方案中选择出最合适的一种，就要根据当前情况选择重点考虑的参数，从而转变成一个多目标优化问题。

2 问题描述与模型建立

打击链在实际过程中的结构可以非常复杂，但从本问题的角度出发，具体的打击链方案事实上满足链式结构，即无论是何种打击链方案，都可以概括为以下结构。

图1 打击链的基本结构

链路模型是打击链方案的基本模型，其采用最简单的串联结构。如图2所示。

图2 打击链的链路模型

2.1 打击链的各项参数计算

首先是打击链的闭环时间为

其中ti表示单个步骤所用的时间，T表示打击链的总时间。n为打击链总的步骤数量。设ti的期望是μi，那么打击链的闭环时间T的期望为

打击链的打击距离为

设di的期望是θi，那么打击链的距离D为

打击链的毁伤概率为

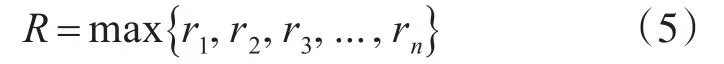
ri表示单个步骤中的探测半径，R为打击链的综合探测半径，n为打击链中的步骤数量。查阅文献资料得知［1～2］，单发导弹杀伤目标的概率为

在此式中，r0为系统误差造成的脱靶量；σ为随机误差的均方差；R0为目标条件坐标杀伤规律参数，通常与导弹和目标特性、相遇条件等有关。多枚导弹杀伤目标的概率为

在式中，P(1，s)是对单个目标射击一次且发射s发导弹时，杀伤单个目标的概率。将P(1，s)作为单个打击链方案的毁伤概率P。

2.2 打击链的全通道误差

本文将打击链的全通道误差分为探测平台定位误差［3］、武器节点定位误差［4］和全流程传输时延误差来进行考虑。

设n步打击链中第i步的三项误差分别为σi探测，σi武器，σi传输，则第i步的全通道误差为

全通道误差为

2.3 问题建模

假定问题场景：

假设存在一敌方目标，我方派出侦察机进行侦察，并在发现目标后配合护卫舰进行拦截。设这组打击链中有n个步骤，这些步骤的集合记为M={m1，m2，m3，…，mn}，步骤mi的完成时间为ti，其中ti为随机变量。

设最优的打击链的步骤集合为X={ma1，ma2，…，mak}，其中ma1，ma2，…，mak为从M中选择的步骤的集合，即满足1＜a1＜a2＜…＜ak＜n且a1，a2，…，ak∈N*。

例如闭环时间最短、打击距离最远的方案，其目标函数为

3 蚁群算法求解最优打击方案

3.1 蚁群算法的基本思路

蚁群算法是一种用来寻找最优路径的概率型算法。这里将打击链的所有方案集合看作有n个节点的有向图，其中每个步骤为一节点，设算法中进行路径搜索的蚂蚁个数为m，用dij表示节点i和节点j之间的距离，在本问题中表示为节点j对应的目标参数的值，初始信息素τij(0)=c（c为常数），初始时刻t为0，每走一步，时刻t增加1。蚂蚁在进行个体搜索时，从当前节点i选择概率值较大的节点j作为下一转移点，概率值的计算公式为

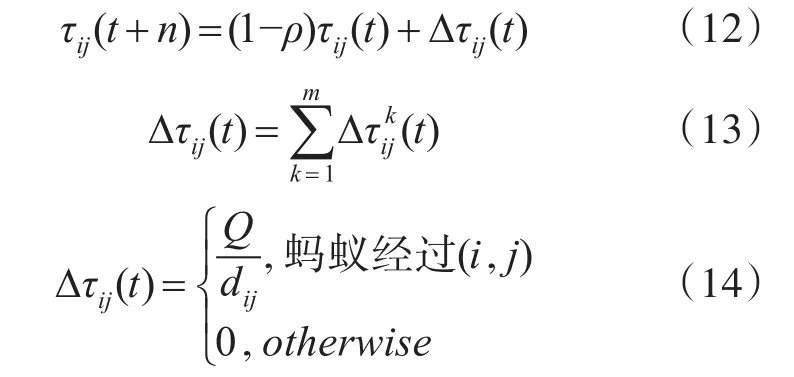
其中ρ为信息素挥发系数，0≤ρ≤1，1-ρ为信息素残留系数；Δτij(t)为本循环中路径（i，j）上带来的信息素增量；为第k只蚂蚁在路径（i，j）上的留下的信息素；Q为信息素强度。

3.2 对蚁群算法的改进

对各节点的初始信息素进行混沌化处理，混沌是指发生在确定性系统中的不可重复、不可预测的随机不规则扰动现象，具有不确定性，其数学表达式为

其中xn为混沌变量，n为迭代次数，μ为控制系统混沌行为的参数，当μ取4的时候，系统处于完全混沌状态［5］。

两点间距离dij计算公式为

在多目标问题中，我们还要动态调整α和β的值，以避免参数值固定导致陷入局部最优，设迭代次数为G，最大迭代次数为Gmax，临界值。

参数α和β的值随着迭代次数的变化在相应的区间里取随机值［6～7］。

为了避免算法陷入局部最优，引入最大-最小蚂蚁系统的概念［8～9］。

设置范围 [τmin，τmax]，此范围为信息素浓度的限定范围［10］，如此，可以保证各条路径上的信息素浓度不会出现过高或者过低的情况［11］。

3.3 算法流程

整个改进之后的蚁群算法的计算过程如图3所示。

图3 多目标问题的蚁群算法流程

4 仿真实验

对第三节中所述算法进行实验，并用模拟退火算法作对比来体现蚁群算法在本问题中的正确性和优越性。根据第二节中对打击链的分析，对一组打击链方案进行仿真，仿真过程意在模拟出一个完整的打击链过程。如图4所示。

图4 模拟打击链完整流程图

此处均要求得到闭环时间最短、毁伤概率最高、全通道误差最小的打击链方案。本章所述仿真过程和算法实现过程均在Windows7系统下Matlab2019软件上完成。所有算法均设置最大循环次数为40。且目标函数值设置为当前打击链评价函数值与全局最优打击链评价函数值之差，故而当差值为0时，问题的Pareto解集基本收敛。具体收敛结果如图5所示。

图5 蚁群算法收敛过程

图6 模拟退火算法收敛过程

可以看出，蚁群算法在迭代次数达到20次左右就以基本收敛，且收敛过程在第7次迭代时信息素浓度达到了一个临界值，从而在后续的收敛过程中，收敛的速度得到了明显提升。蚁群算法得出非劣解集为打击链3、5、6、8。

可以看出，模拟退火算法的收敛过程相对较为平缓，在第3次循环过程中出现了比较急剧的变化。模拟退火算法得出非劣解集为打击链3、4、5、8。

通过以上几种算法的实验结果可以看出蚁群算法的收敛速度更快，对比两种算法得出的非劣解集可以看出，蚁群算法和模拟退火算法解集有50%吻合，考虑到算法间的差异性，此解集可以认为是可行解，故在保证正确性的情况下，改进后的蚁群算法是更好的那一种算法。

5 结语

本文为了研究出最适合解决打击链方案最优选择问题的方法，选择了蚁群算法和模拟退火算法作对比，之后通过实验可以看出优化后的蚁群算法在收敛速度上有明显优势，故本文倾向于选择蚁群算法来对打击链方案选择问题进行处理。