基于两阶段DEA 的城市轨道交通系统效率评价研究

叶嘉栋，范小舟

（武汉纺织大学 外经贸学院，湖北 武汉 430000）

1 文献综述

城市轨道交通系统是指在城市中使用车辆在固定导轨上运行并主要用于城市客运的交通系统。城市轨道交通系统具有初始投入高，建造周期长，服务范围广等特点，对缓解城市交通拥堵和促进地方经济发展都具有重要意义，其系统效率评价工作具有极高的研究价值。

目前，国内外学者研究城市轨道交通系统效率评价的方法主要为数据包络分析（DEA）法。该方法的研究对象主要是多投入多产出系统，测算同质决策单元（DMU）之间的相对有效性。叶嘉栋（2020）运用DEA-TOPSIS 法，对全国16 个城市的轨道交通系统效率进行实证分析；邹玉婷（2020）基于PCA-DEA 法，进行了生产效率分析、松弛变量分析和超效率DEA 分析。

然而，上述研究均基于单阶段DEA 方法。该类方法将整个城市轨道交通系统看做一个“黑箱”进行处理，仅从系统整体的投入、产出考察整个系统运行效率，忽略了系统内部过程和过程间的相互关系。为解决这一问题，本文引入两阶段DEA 对DMU 的内部结构进行分解。

本文的贡献在于：首次从两阶段视角出发，将轨道交通系统的运作过程分成建设阶段和运营阶段两个阶段，采用两阶段DEA 模型，构建两阶段城市轨道交通系统效率评价体系；测算出全国主要城市轨道交通系统的综合效率和子阶段效率；找出全国主要城市轨道交通系统内部存在的问题，并根据不同城市的实际情况，提出相应改进措施；为我国城市轨道交通系统的建设和发展提供科学借鉴。

2 模型构建、指标体系及数据来源

2.1 模型构建

假设现有n 个同质决策单元，记为DMU(j=1,2,…,n)，DMU中包含m 个投入，记为 x(i=1,2,…,m)，s 个最终产出，记为 y(r=1,2,…,s)，D 个中间产出（即第一阶段产出），记为 z(d=1,2,…,D)，λ为投入权重向量，μ为产出权重向量，DMU为待测DMU，则两阶段DEA 模型可以表示为：

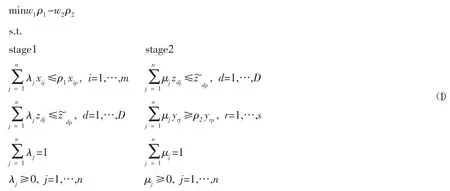
其中，ρ、ρ分别为第一子阶段效率值和第二子阶段效率值。w、w分别为第一子阶段权重和第二子阶段权重，反映了子阶段间的相对重要程度，可以根据实际需要来人为设定，需要特别指出的是，该模型的第一子阶段是投出导向模型，因此ρ取最小目标函数值；第二子阶段是产出导向模型，因此ρ取最大目标函数值，故在整体目标函数表达式中，第二阶段的效率部分加上了负号。模型（1）打开了决策单元的“黑箱”，将“黑箱”解构为互相关联的两个子阶段，相较于单阶段DEA 模型能够更为深入、客观地解析系统的内部过程。

2.2 指标体系

在对决策单元进行DEA 测度的时候，投入产出指标体系的构建至关重要。现有研究主要是从单阶段视角出发，聚焦于已建成的城市轨道交通系统为城市所带来的经济效益和社会效益。该过程只考虑到了城市轨道交通系统实际运营过程中的投入产出，而忽略了城市轨道交通系统建设阶段所投入的巨额建设成本。据此，本文在上述文献的基础上，将城市轨道交通系统的运作过程分成建设阶段和运营阶段两个子阶段。两阶段模型相较于上述单阶段模型能够反映出财政投入和人力投入所带来的经济效益和社会效益产出。综合考虑数据的有效性、可获得性及完整性后，本文构建如下投入产出指标体系，如表1 所示：

表1 城市轨道交通系统投入产出指标体系

第一阶段为建设阶段，将建设过程中投入的建设资金和建设人力作为建设投入，将已建成的城市轨道交通系统中的线路长度和车辆数作为建设产出。分别从线路覆盖域大小和荷载客流强度两个方面对建设效果进行考察。第一阶段所得到的效率值是城市轨道交通系统的建设效率值。

第二阶段为运营阶段。将已建成的城市轨道交通系统中的线路长度和车辆数作为运营投入，将年票价收入和年客运量作为运营产出，分别从经济效益和社会效益两个方面对运营效果进行考察。第二阶段所得到的效率值是城市轨道交通系统的运营效率值。具体的两阶段模型示意图如图1 所示：

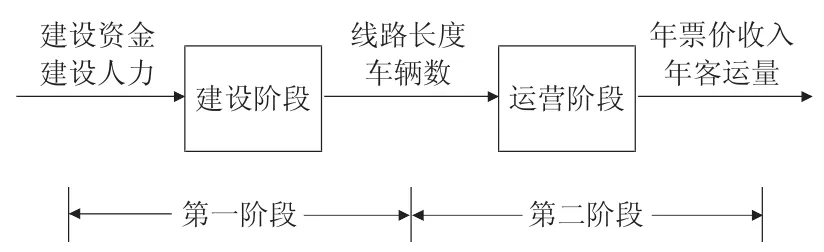
图1 城市轨道交通系统两阶段模型示意图

2.3 数据来源

本文选取2020 年全国16 个主要城市（见表2）的城市轨道交通系统作为研究样本，其中，数据来源于中国城市轨道交通协会发布的《城市轨道交通2020 年度统计和分析报告》和各城市2020 年交通发展年报。

3 实证分析

本文运用Matlab 软件分别对进行模型（1）进行求解，测算出2020 年全国主要城市轨道交通系统的综合效率、建设效率和运营效率，并对其效率进行排名，如表2 所示：

表2 2020 年全国主要城市轨道交通系统效率测算及排名

由表2 可知，从“黑箱”分解的结果来看，样本中所有DMU 的建设效率均值为0.8691，共有8 个DMU 建设效率有效，建设有效率为50%；运营效率均值为0.8296，共有5 个DMU 运营效率有效，运营有效率为31.25%，无论是从效率均值还是从有效率来看，样本中DMU 建设阶段的整体表现都要优于运营阶段的整体表现。这说明综合效率的无效性主要是由运营阶段的无效引起的。

结合上述分析，本文运用波士顿矩阵法，以样本中所有DMU 的建设效率均值（0.8691）和运营效率均值（0.8296）为分界点，将各城市轨道交通系统分为高效率和低效率两个等级，并将样本中全部DMU 分为以下四类，即高建设效率—高运营效率、高建设效率—低运营效率、低建设效率—高运营效率和低建设效率—低运营效率四种类型，分类情况如图2 所示：

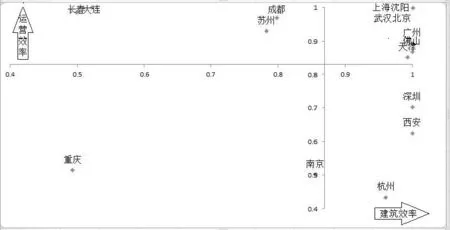
图2 2020 年全国主要城市轨道交通系统子阶段效率二维分布图

由图2 可知属于高建设效率—高运营效率分类的DMU 共有北京、天津、沈阳、上海、武汉、广州和佛山7 座城市，占到样本总体的43.75%。上述城市在建设效率和运营效率两个方面都处于全国领先地位，是其他城市轨道交通系统学习的标杆。

属于高建设效率—低运营效率分类的DMU 共有西安、杭州和深圳3 座城市，占到样本总体的18.75%。对于该类型的城市，在运营阶段，线路管理人员应对提高早晚高峰时段的拥挤线路的发车频次，防止站台拥堵；降低部分空闲时段的发车频次，防止列车空载；通过在轨道交通站点附近设立公交换乘点、共享单车停靠点和私家车停靠点，提高乘客出行的换乘效率，进一步提高运营效率。

属于低建设效率—高运营效率分类的DMU 共有长春、大连、成都和苏州4 座城市，占到样本总体的25%。对于该类型的城市，在建设阶段，工程管理人员应当制定完备的施工计划和应急预案，避免由工期过长和突发情况所造成的效率低下；合理调度和配给建设资源，避免资源的空置或冗余；通过完善相应的激励和监督机制，提高施工团队的劳动积极性，进一步提高建设效率。

属于低建设效率—低运营效率分类的DMU 共有重庆和南京2 座城市，占到样本总体的12.5%。对于该类型的城市，应在综合考量上述建议同时，针对市内部分老旧线路、列车进行升级改造，通过技术更新、管理创新、运营优化等一系列措施改变目前系统的低效态势。

4 结论

本文从两阶段视角出发，构建两阶段城市轨道交通系统效率评价体系，测算出2020 年全国16 个主要城市轨道交通系统的综合效率和子阶段效率，并采用波士顿矩阵法对这些城市进行分类，提出政策建议。综合上述分析，本文有以下两点结论：

（1）“黑箱”分解的结果显示，样本中建设效率均值和运营效率均值分别为0.8691 和0.8296，建设有效率和运营有效率分别为50%和31.25%。综合效率的无效性主要是由运营阶段的无效引起的。

（2）子阶段效率分类结果显示，样本中处于高建筑效率高运营效率分类的城市共有7 座，占样本总数的43.75%。超过半数的城市轨道交通系统都存在投入冗余或产出不足的情况，有较大的改进空间。各地应结合自身短板，进一步提升轨道交通系统效率。