“货到人”订单分批拣选作业优化研究
2022-09-06赵洪銮李晓君宿梦梦
邹 炜,赵洪銮,李晓君,宿梦梦
(山东建筑大学 计算机科学与技术学院,山东 济南 250101)
0 引言
随着电商行业的迅速发展,电商企业需要处理数量众多且种类繁杂的订单,物流行业也面临着巨大压力。订单拣选作业时间约占总作业时间的30%~40%,拣选作业成本约占到总作业成本的60%。为加快订单拣选作业速度和降低拣选作业所需成本,研究主要集中在订单分批、拣选路径、仓储布局和储位规划四个方面。订单分批通过将多张订单组合在一个批次,可以有效缩短拣选时间;合理规划的拣选路径可以快速完成订单拣选任务、减少重复行走;仓储布局决定了仓库中货架如何摆放,行走通道如何分布,影响着拣选路径的行驶总距离;储位规划是将出入库频率高的货物存放在仓库入口附近,遵循上轻下重的原则。
目前,订单拣选作业方式正从“人到货”向“货到人”方向发展。在传统的“人到货”拣选作业中,拣货员推动拣货小车进入仓库的存储区,根据订单信息将所需商品拣选出来。“人到货”订单拣选作业方式需要大量的拣货员,存在拣货效率低、准确度低、人工成本高等问题。“货到人”拣选作业通过AGV 小车或机器人等设备搬运移动货架到拣选台,拣货员在拣选台依据订单信息对移动货架中的商品进行拣选,提高了订单拣选作业的效率和准确度,降低了人工成本,并且消除了“人到货”订单拣选模式对拣货员工作经验的高度依赖。在“货到人”订单拣选作业模式下,移动货架搬运前需要根据订单信息对订单进行合理分批,减少货架搬运次数,提高订单拣选效率。因此,如何实现订单分批是本文研究的重点。
总结相关文献发现,国内外求解订单分批的模型方法主要有两种,第一种是求解以最小化货架搬运次数为目标的订单分批数学模型,第二种是求解以最大化订单相似度为目标的订单分批数学模型。张彩霞在“货到人”模式下以AGV 小车搬运货架的总次数最少为目标建立数学模型,通过节约算法对模型进行求解,与不分批的订单搬运货架次数相比提高了33%;徐冉建立了以货架搬运次数最少为目标的订单分批模型,使用相似性规则实现初始订单分批,然后对初始订单分批采用变邻域搜索算法进行优化;秦馨以搬运货架总次数最少为目标,通过设计遗传算法对订单分批进行求解,完成订单拣选作业;王旭坪运用固定时间窗规则,同时考虑了相似度和订单紧急程度等多个因素,构建数学模型进行求解;韦超豪对订单分批优化使用了Canopy 算法和K-means 聚类算法来对订单进行聚类,求解订单分批结果;邵泽熠、董宝力构建了以订单相似度最高为目标的分批拣选优化模型,并采用改进遗传K-means 算法进行求解;马廷伟、朱友琼也根据订单相似度建立订单分批模型。
本文以货架搬运总次数最少为目标建立数学模型,首先根据订单之间的关联性,最大化订单间相似度并求解订单分批模型,然后采用萤火虫算法优化订单初始分批结果,进而得到最终订单分批求解结果。
1 问题描述
货到人模式下的订单分批问题可以描述为:仓库中有X种商品,存储在Y 个货架上,每个货架的储位数量有S 个,储位只能摆放一种商品。在离线状态下,已知订单信息和商品摆放在货架的具体位置,如何对M 张订单进行合理分批,才能使机器人搬运货架次数最少。
为简化问题,对货到人订单拣选作业模式下订单分批问题作出下列假设:
(1)离线状态下订单信息均已知,如仓库中订单数量、商品种类、商品存储在货架的具体位置。
(2)单个订单不可分割,每个订单只允许存放在一个批次内。
(3)订单所需商品不存在缺货的情况。
(4)同一个货架的每一层只存放一种商品,不同层可以存放不同商品。
(5)不存在紧急插单的情况。
(6)每个批次内所有的订单数量不大于拣选台周转货架的储位数。
数学模型中参数和变量定义如表1 所示。

表1
2 订单分批模型建立
为提高“货到人”订单拣选作业效率,将多个订单进行分批处理,机器人依据订单分批处理结果和已知的订单信息将移动货架搬运到拣选台完成订单拣选作业。以货架搬运次数最少为目标建立订单分批数学模型,首先按照最大化相似度对订单进行分批,然后设计萤火虫算法对初始订单分批结果进行优化,减少货架总搬运次数。
目标函数:最小化货架搬运总次数:

约束条件:

决策变量:

公式(1)是订单分批数学模型的目标函数,即最小化货架总搬运的次数;公式(2)约束了每个订单只能存放在一个批次内;公式(3)约束了每个批次内的货架只能进行一次或零次搬运,不能重复搬运货架;公式(4)约束了每个订单批次内所包含的订单数量,不允许超过拣选台的储位数P;公式(5)约束了每个订单包含的商品种类不超过所属批次含有的商品种类数;公式(6)至公式(8)是决策变量,取值都为0 或1,当取值为1 时,符合条件,公式(6)判断订单Z 是否被划分到订单批次N 中;公式(7)判断订单批次N 是否搬运货架Y;公式(8)判断订单批次N 是否包含商品X。
3 基于订单相似度的订单分批求解
根据已知的订单信息和商品摆放在货架的具体位置,按照订单相似度规则划分多个订单,将订单相似度最大的订单组合在同一个批次内实现订单分批,多个订单划分在同一个批次,可以有效减少货架所需搬运的次数。Xiang Xi 等(2018)提出了一种订单相似度计算方法,本文也使用该计算方法:
订单相似度O=每个订单内部的相似度O1+两个订单之间的相似度O2
每个订单内部的相似度是指订单包含的商品在同一个货架上的商品对数,两个订单之间的相似度是指将任意两个订单的商品组合在一起,计算在同一个货架上的商品对数。
订单相似度计算方法举例说明:每个货架可以存放五种商品,每个货架按商品编号1-5,6-10,11-15,16-20……依次存放商品,有2 张订单A={12,17,18,27},B={11,13,26,28,30},计算订单A、B 的订单相似度:O1={17,18}=1,O1={11,13}、{26,28}、{26,30}、{28,30}=4,O2={11,12}、{11,13}、{12,13}、{17,18}、{26,27}、{26,28}、{26,30}、{27,28}、{27,30}、{28,30}=10,O=O1+O1+O2=1+4+10=15。原本未分批时订单A、B 需要搬运货架为3+2=5 次,依据订单相似度最大划分为同一批次订单后,需要搬运货架3 次,减少了2 次货架搬运。
将A={60,12,58,45,89},B={56,97,47,59,33},C={6,85,100,34},D={24,91,21,10,7},E={94,77,93,70},F={92,95,90,68}6个订单进行分批,通过计算订单相似度可以分成3 批订单n={A,B},n={C,D},n={E,F},进行分批前货架需要搬运货架21次,分批后需要搬运货架17 次,节约了4 次。分批过程如图1 所示:
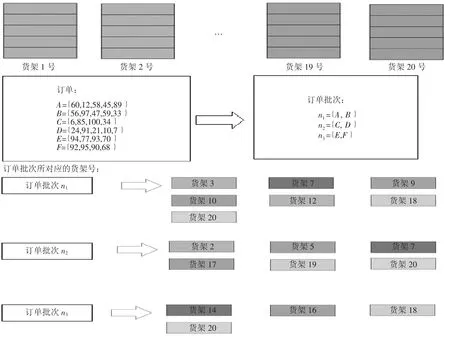
图1 订单分批过程
订单相似度求解订单分批问题的步骤:
Step1:根据已知的订单信息,货架的位置信息和拣选台周转货架储位数决定每个批次内包含订单数量的最大限度;
Step2:计算所有订单之间的相似度,构建订单相似度矩阵;
Step3:找到订单相似度矩阵中值最大对应的订单m、m;
Step4:判断m、m是否属于已有订单批次集合,如果是则将订单m或m分别添加至对应的订单批次中,否则将订单m、m划分为同一批次,构建新的订单批次;
Step5:在构建订单批次的同时要判断是否满足周转货架储位数P 的限制,如果是则继续添加新订单,否则删除超出限制的订单,将被删除的订单构建成新的订单批次;
Step6:返回,循环上述操作直至所有订单都被划分;
Step7:输出所有订单批次集合B。
4 基于萤火虫算法的订单分批求解
4.1 萤火虫算法
萤火虫算法属于启发式算法,为模拟萤火虫在自然界中的发光特性而提出的群体智能优化算法。目前,萤火虫算法主要有两种,一种是在2005 年,印度学者K.N.Krishnanand 和D.Ghose 在IEEE 群体智能会议上提出了一种新的群智能优化算法,人工萤火虫群优化算法(Glowworm Swarm Optimization,GSO);另一种是在2009 年,剑桥学者Xin-She Yang 根据自然界中萤火虫的发光行为提出萤火虫算法(Firefly Algorithm,FA),两种算法研究思路大体一致,但在实现方式上略有不同。本文采用第二种萤火虫算法(FA),根据萤火虫自身所特有的发光和吸引行为等生物特征设计了该算法,萤火虫个体的亮度和吸引力决定了该萤火虫的吸引行为,通常萤火虫亮度由它所处位置的目标函数值决定,萤火虫亮度越高,它所处的位置也就越好,目标函数值也相对较好,当某个萤火虫比周围其他萤火虫更亮时,更容易吸引其他萤火虫向自身移动,如果出现多个萤火虫亮度相同的情况,则萤火虫进行随机移动。
为方便萤火虫算法的实现,Yang Xin-She 提出了以下三条规则:
(1)所有萤火虫个体不区分雌雄,任意一只萤火虫都可能被其他萤火虫所吸引。
(2)对于任意两只萤火虫,较亮的萤火虫会吸引较暗的萤火虫。如果所有萤火虫亮度都相同,它们就会进行随机移动。
(3)萤火虫个体的亮度受目标函数值影响。
4.2 萤火虫算法的相关数学定义:
定义1 萤火虫的相对荧光亮度为:

其中:I是萤火虫i 的绝对亮度;γ 是光强吸收因子;r是萤火虫i 和j 之间的欧式距离。
定义2 萤火虫之间的相对吸引力为:

其中:β为最大吸引力,是光源处,即r=0 时的吸引力,γ、r的意义同上。
定义3 萤火虫j 被萤火虫i 吸引,萤火虫j 的位置更新为:
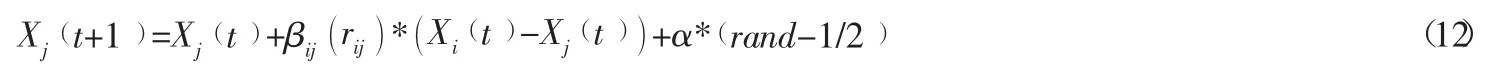
其中:t 为算法的迭代次数,X()代表萤火虫j 在第t+1 次迭代的位置;β是萤火虫i 对萤火虫j 的吸引力;α 为常数,取α∈[0,1];rand 是在[0,1]上服从均匀分布的随机因子。
4.3 萤火虫算法设计求解
订单分批问题属于NP-hard 问题,订单数量越多,计算量会呈指数增长,对其求精确解十分困难,通常选择启发式算法对其进行求解。本文采用萤火虫算法对订单分批问题进行求解,得到优化的订单分批结果。
4.3.1 萤火虫算法的编码
本文求解的问题是货到人订单拣选作业最小化货架总搬运次数,结合萤火虫个体的位置进行编码求解该问题。建立个体位置与问题解之间的映射关系,采用实数编码方式,随机生成系统需要拣选的订单和商品,使萤火虫初始分布具有随机性。
4.3.2 萤火虫算法的解码
萤火虫算法的解码是算法解空间转变为实际问题解空间的过程,在解码的同时要考虑拣选台周转货架储位数,即订单批次中含有订单数量的最大限度。每个萤火虫的位置都是问题解空间的一个解,对萤火虫位置进行解码,计算目标函数值。
4.3.3 萤火虫算法的个体亮度
订单分批问题的目标是求解最小化问题,萤火虫算法的发光亮度设计为每个萤火虫个体对应的货架搬运总次数的倒数。萤火虫亮度的高低决定了所在位置的好坏,影响着萤火虫个体的移动方向,萤火虫个体之间的移动距离与吸引力有关,通过迭代更新亮度和吸引力来寻找订单分批问题的最优解。

由公式(9)可知,萤火虫个体的亮度与萤火虫之间的距离有关,公式(10)中萤火虫之间的距离采用欧式距离,为方便计算,萤火虫个体之间的距离定义为计算同一位置上不同数字的总个数之和。举例说明,如Z=[1,2,1,3,4,1,2,5]、Z=[1,2,3,3,4,1,3,5],萤火虫Z、Z之间的距离为R=2,数字不同的位置分别是3 和7。
4.3.4 萤火虫算法的个体更新
(1)吸引移动
假设萤火虫i 当前的位置为p,在邻域范围内,寻找更亮的萤火虫j 并计算两者之间的距离r,记录所有比萤火虫i 亮的萤火虫,找到最亮萤火虫k 后并朝着萤火虫k 方向移动一步。在具体实现过程中,亮度较小的萤火虫为了向更亮的方向移动,通过寻找两个解中批次不一致的订单号,按照更亮萤火虫的解进行更新。
(2)随机移动
对于邻域范围内最亮的萤火虫k 进行随机移动,随机移动就是对不同批次内的两个订单进行随机替换,避免陷入局部最优。举例说明随机移动:订单批次 1={[1,23,5,7]、[2,4,16,8]、[13,6,9,12]},订单批次 2={[12,3,26,27]、[11,13,17,18]、[19,10,22,21]},对订单批次 1、2 的第2 个订单进行交换得订单批次 1={[1,23,5,7]、[11,13,17,18]、[13,6,9,12]},订单批次 2={[12,3,26,27]、[2,4,16,8]、[19,10,22,21]}。
4.3.5 萤火虫算法的终止条件
本文终止条件是判断是否达到最大迭代次数或存在更优的目标函数值,如果满足终止条件,则输出货架搬运次数、分批批次和订单批次内所包含的具体订单,否则继续迭代。
4.4 订单分批的实现
萤火虫算法求解步骤:
Step1:初始化算法参数。设置萤火虫个体数目m,光强吸收因子γ,最大吸引力β,最大迭代次数max_gen。
Step2:初始化种群。萤火虫算法的初始种群设置为最大化订单相似度实现订单分批的批次集合。
Step3:根据萤火虫个体的位置信息计算萤火虫的亮度,即目标函数值货架搬运总次数。I是各个萤火虫的最大发光亮度,将萤火虫按照目标函数值进行排列,找到并记录当前最优解f及其所在种群中的位置。
Step4:计算萤火虫之间的距离和相对发光亮度,找到最亮的萤火虫k,确定萤火虫的移动方向。
Step5:计算萤火虫的吸引力并更新萤火虫的位置信息。
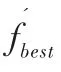
Step7:判断当前最优解是否满足拣选台周转货架储位数P 的限制,如果满足则继续执行下一步操作,否则删除超出限制的订单。
Step8:当满足最大迭代次数后,转Step9,否则转Step3。
Step9:萤火虫算法迭代完成,输出最优解。
求解订单分批问题的整体流程图如图2 所示。

图2 求解订单分批模型流程图
5 实验结果分析
在Matlab 软件上进行多组仿真实验,验证采用订单相似度和萤火虫算法实现订单分批问题的有效性和可行性。
5.1 实验参数设置
根据仓库订单拣选系统实验环境设置参数,如表2 所示:

表2
订单分批实验可以描述为:在拥有60 个货架、300 种商品的订单拣选仓库中,商品按照1-5,6-10,11-15,16-20,…,56-60 的顺序依次存放在60 个货架上,若干个机器人对移动货架进行搬运实现订单分批。现在需要对40 个订单进行分批,完成拣选作业的订单分批任务。
5.2 订单分批模型求解
5.2.1 订单批次划分结果
以订单相似度为划分依据,建立最小化货架搬运总次数为目标的数学模型。40 批订单可以划分成5 批,货架搬运次数为69 次;按照原始订单进行拣选,货架搬运总次数为160次;与按单拣选搬运货架总次数相比,优化了56.8%。由于拣选台处周转货架个数为10,所以划分批次内所含订单的最大数量为10,批次内所含订单个数最少为1。为减少货架搬运总次数,订单批次内订单数量越多,订单分批批次数量越少,从而减少货架搬运次数。
在Matlab 软件上按照订单相似度最大实现订单分批实验结果如图3、表3 所示。
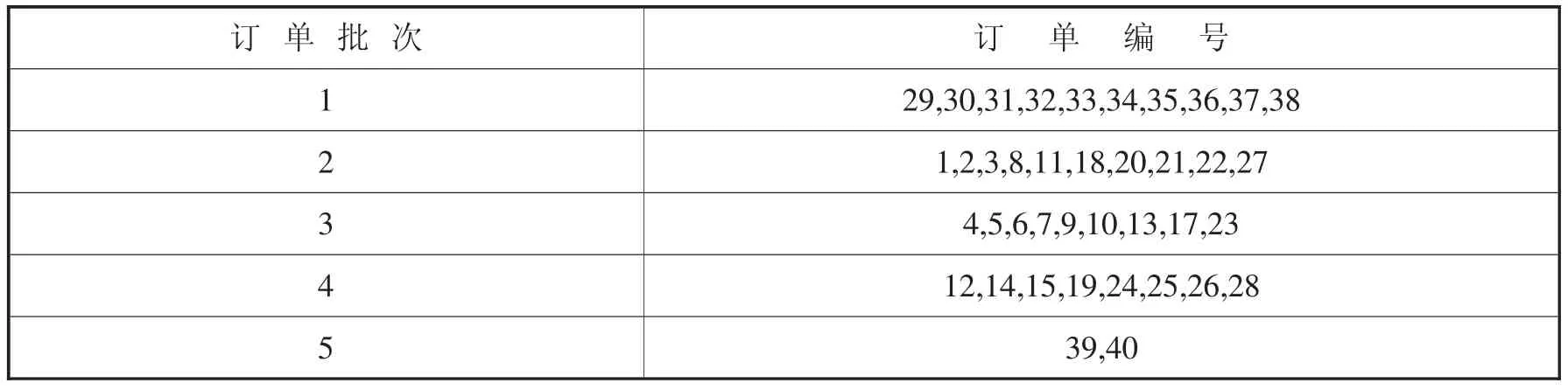
表3 订单分批结果
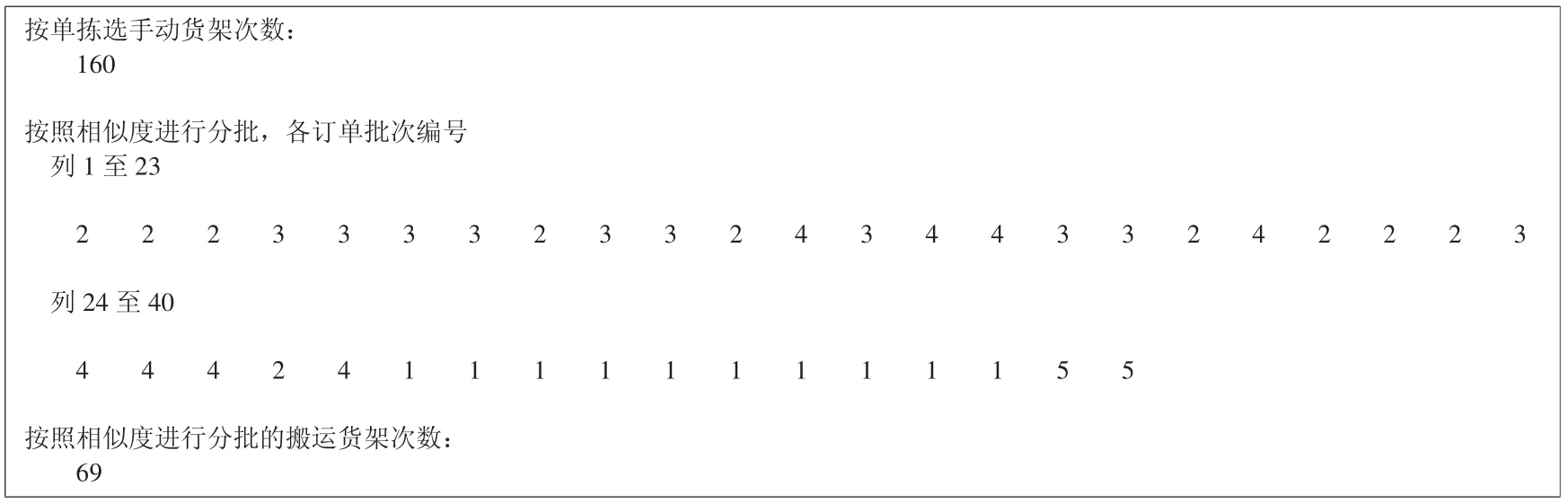
图3 订单相似度方法实现40 个订单的分批
采用萤火虫算法对订单相似度分批结果进行优化,40 个订单划分为4 批,优化后货架搬运总次数为64 次。与初始状态货架搬运次数160 次比较,萤火虫算法优化了60%,与按照订单相似度划分实现订单分批相比,减少了5 次货架的搬运,优化了7.2%。
在Matlab 上采用萤火虫算法优化订单分批实验结果如图4、表4 所示。

表4 优化后订单分批结果

图4 萤火虫算法实现40 个订单的分批
5.2.2 订单拣选系统参数影响与效果分析
(1)订单数量对货架搬运次数的影响
电商行业每天面对的订单数量具有波动性,订单拣选系统每天需要处理不同数量的订单,为了验证所提方法的有效性,继续对20 个、40 个、100 个订单分别进行分批。
分析比较在20、40、100 个订单按照三种拣选方式实现订单分批所需货架搬运次数,如图5 所示。
通过图5 可以发现,随着订单数量的增加,按单拣选、按订单相似度拣选和萤火虫算法拣选实现订单分批所需搬运的货架次数逐步提升;订单数量分别为20、40、100 时,与按单拣选搬运货架次数相比,以订单相似度为划分依据实现订单分批分别优化了53%、56.8%、55.5%,萤火虫算法优化实现订单分批都优化了约60%。发现订单量从20 到40 之间,优化效率逐步提升,当达到100 时,优化率反而下降了,即当订单量达到合适值时,可以达到优化效果最大化,提高“货到人”订单拣选作业效率。

图5 不同订单数量之间分析对比图
(2)拣选台处周转货架数量对货架搬运次数的影响
拣选台处周转货架数量决定了订单批次中包含订单数量的最大限度,将越多的订单划分在同一批次可以减少货架的重复搬运,所以拣选台处周转货架的数量影响着批次划分后机器人搬运货架的次数。为了验证所提模型的有效性,分别在10、15、30 个周转货架上进行实验,对比分析不同周转货架数量所需的货架搬运次数,寻找二者之间的关系。
如图6 所示,分别比较使用10、15、30 个周转货架个数对实现订单分批货架搬运次数的影响。

图6 不同周转货架数量之间分析对比图
整体来说,在一定的范围内,随着周转货架数的增加,货架搬运次数逐渐减少,若超出某一阈值,货架搬运次数优化效果反而不好。如周转货架数增加到30 个时,与订单相似度所需搬运货架次数相比,萤火虫算法优化后货架搬运次数反而增加,不仅增加了设备成本,还降低了订单分批作业的效率。因此,合适的周转货架数量对于提高“货到人”订单拣选作业效率和准确度十分重要。
6 结论
本文研究了关于“货到人”订单拣选作业的订单分批问题,合理有效的订单分批可以提高订单拣选作业的效率,通过将多张订单合并在一个批次内进行拣选,可以减少货架搬运总次数。以最小化货架搬运总次数为目标,建立订单分批数学模型,首先考虑订单之间的关联性,以订单相似度最大为分批依据实现订单分批,与按单拣选货架搬运总次数相比优化率可达53%~57%,然后对订单相似度实现的分批结果进行再优化,采用萤火虫算法优化订单批次,与初始货架搬运次数相比提高了60%,效果十分明显。经过在Matlab 软件上进行多组数值实验,验证了所提模型的可行性和设计算法的有效性。在以后的工作中,可以考虑与机器人拣选路径的联合优化来提高订单拣选作业的效率和准确性。
