“三教”改革背景下极限的计算方法教学探索

程 婧

（西安城市建设职业学院基础课部 陕西 西安 710114）

“三教”改革事关职业教育的“谁来教”“教什么”和“怎么教”，直接影响教育教学质量，是新时代职业教育改革发展的关键。

高等数学作为高职高专院校数学教育最重要的一门公共基础课程，如何通过有效的教学方式帮助学生通过高等数学的学习，养成一定的数学思维并能够将其结合专业相关问题运用到实际生活中，是值得高校教师关注和思索的问题。

极限的概念是高等数学中微积分的理论基础，微积分的一些重要概念都是建立在极限概念的基础上。针对不同类型函数，求解极限的计算方法也不同。本文教师在教法上进行探索，利用探究式、启发式、讨论式等教学方式，给出函数极限的几种计算方法，并总结出当有多种计算方法时，如何有清晰思路对计算方法进行正确合适的选择，使得极限计算更简便。

1 直接代入法求极限

对于有理函数（多项式）或有理分式函数，求函数当时的极限可以将=直接代入计算函数在该点处的函数值。

引导学生讨论：极限计算中出现的0，是否表示函数恒为0？（在讲解知识时通过不断提问可使学生思维得到锻炼）

结论：函数在自变量变化过程中极限为0，表示的是函数在变化过程中的变化趋势无限接近于0，不是函数恒为0。并且引出方法二。

2 利用无穷小与无穷大的关系求型极限

2.1 知识储备

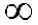
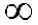
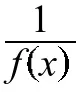
2.2 结论

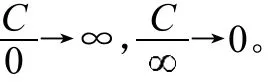
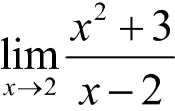
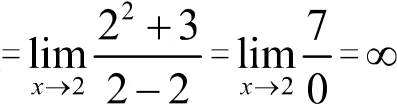
3 用因式分解方法求型极限

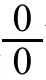
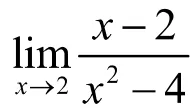
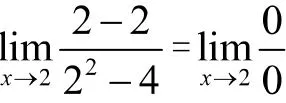
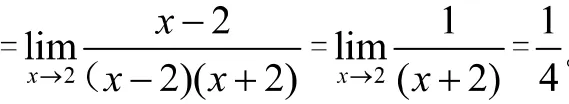
4 用等价无穷小代换求函数极限

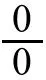
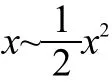
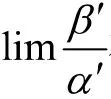
即当函数求极限时，出现可以进行等价无穷小代换的量，可以优先进行等价代换后，约分，再直接代入求出极限。

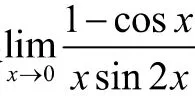
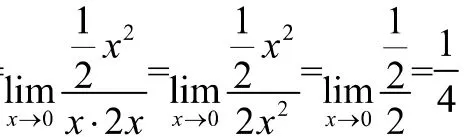
注意：等价无穷小代换求极限可以简化极限的运算，但是在使用时有条件限制：

①被代换的函数必须是无穷小，即极限为0。

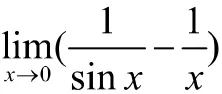
5 用洛必达法则求解未定式极限

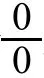
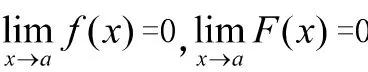
（2）在点的某去心领域内，和都存在且≠0；

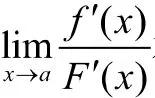
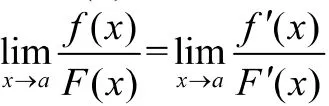
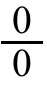
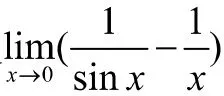
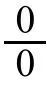
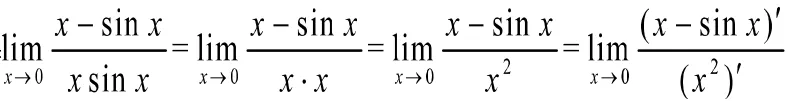
6 利用无穷大的倒数是无穷小求型极限

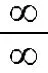
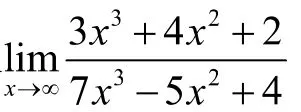
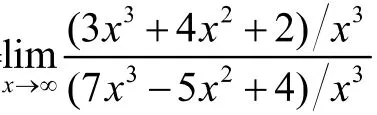
7 利用重要极限求极限

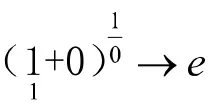
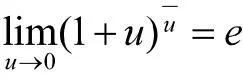
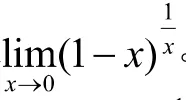
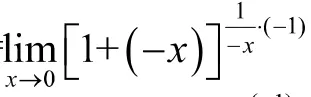
8 利用无穷小的性质求极限

定理 有界函数与无穷小的乘积是无穷小。

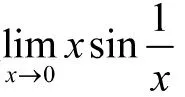
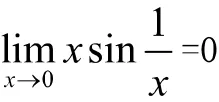
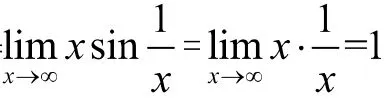
9 含有变上限积分函数的极限计算方法

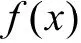
含有变上限积分函数的极限计算方法为：第一步，利用洛必达法则对分子分母分别求导，对分子求导时利用定理一代二导，其中一代表示将积分上限代入被积函数，二导是积分上限的导数；第二步，根据极限类型，对应选取最适合的方法计算极限。

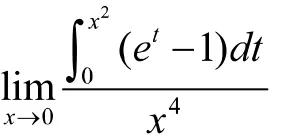
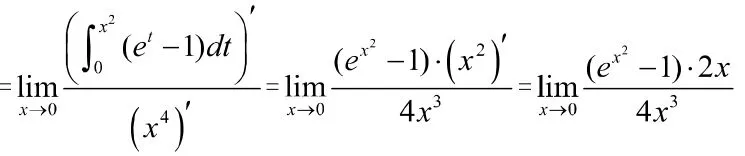
10 总结

本文在“三教”改革背景下，以提高高等数学课堂教学质量为目标，积极探索不同类型函数在求极限时的计算方法，始终带领学生沿着发现问题→思考问题→解决问题的主线，旨在通过逻辑严谨的多样式教学方法，由浅入深地带领学生去思考、探索、实践，在过程中以学生为中心培养一定的数学思维能力，以及发现问题解决问题的能力，达到立德树人的根本目标。在以上几种计算极限的方法中，我们发现，选择合适的计算方法可以简化计算获得事半功倍的效果，现将如何选择适当的极限计算方法思路总结如下：

（1）当函数中出现符合等价无穷小代换的量时，优先进行等价无穷小代换（要注意等价无穷小代换的前提条件：（方法四）；（2）当极限中出现变上限积分时，用洛必达法则对分子分母同时求导，变上限积分求导时分两步（一代二导）（方法九）；（3）直接代入后，根据极限不同类型对应选择不同的计算方法（见表1）。

表1