基于混沌与快速小波变换的多光谱图像压缩加密算法

徐冬冬， 于 欣*， 杜丽敏, 毕国玲

1. 长春大学， 吉林 长春 130022 2. 中国科学院长春光学精密机械与物理研究所， 吉林 长春 130033

引 言

多光谱成像系统作为卫星的重要组成部分正朝着高分辨率、 大视场角的方向发展。 高分辨率可以得到更加详细和准确的信息， 提高对地面和海洋目标的识别能力； 大视场角可以使空间相机的覆盖范围更大， 有效提高工作效率。 而随着分辨率和视场角的提高， 导致空间相机输出的数据量越来越大， 这就对相关图像的压缩及解压算法提出了更高的要求。

此外， 由于某些侦察监视工作不希望被其他国家或者组织破解， 因此除了通信链路加密之外， 非常有必要对多光谱图像进行加密， 以确保数据的安全性。 与此同时， 地面对空间传回的数据量、 数据质量以及安全性的需求越来越高， 对算法的压缩效率、 计算复杂度、 稳定性、 密钥空间以及敏感性提出了更高的要求， 因此研制出压缩效率高、 计算复杂度低、 稳定性强、 密钥空间大、 对密钥和明文敏感高的加密算法是目前迫切需要解决的问题。

针对二维图像和多光谱图像， 提出了很多压缩加密算法。 郭家伟等提出了与联合图像专家组(joint photographic experts group， JPEG)压缩相结合的图像加密算法[1]， 首先将像素点的RGB分量以8×8的子块为单位在行列方向上进行位置置乱, 实现颜色分量重组, 再进行JPEG压缩； 完成离散余弦变换(discrete cosine transform， DCT)系数量化后， 分别对DC系数和AC系数进行位置置乱， 再对DCT系数的符号位进行随机修改。 该算法加密效果好， 密钥空间大， 敏感性强， 但压缩效率不足。 Song等提出了基于熵编码和压缩感知的图像压缩加密方案， 具有较好的压缩加密性能[2]， 但在去冗余方面仍存在一定的不足。

由于传统的多光谱数据传输和存储只是压缩， 而没有考虑到“压缩—解压缩”过程引起的图像安全性问题。 对于压缩域的多光谱遥感图像数据而言， 其主要应用目的是对地物分类和目标识别， 因此保留多光谱图像数据中的纹理信息是非常重要的。 如何在保留用于分析的重要信息的前提下进行压缩域的多光谱图像数据加密是具有挑战性的工作， 研究面向应用的压缩域多光谱遥感图像方法和技术， 不仅能够对海量的多光谱数据进行有效的压缩， 而且有利于保证多光谱图像链路传输时的安全。

上述压缩加密算法对二维图像的压缩加密效果较好， 对于多光谱图像的压缩加密效果欠佳； 同时， 针对多光谱图像的压缩加密算法， 在压缩效率或加密效果方面存在不足。 与普通图像相比， 多光谱图像有两种冗余， 即空间冗余和光谱冗余， 因此压缩时只有兼顾这两部分冗余， 才能使压缩性能最佳。 有些算法， 如PCA或独立成分分析， 只通过降维实现压缩， 忽略了空间相关性， 因此， 压缩效果一般。 随后， 兼顾空间相关性与光谱相关性的压缩算法应运而生， 如3D多级树集合分裂(3D set partitioning in hierarchical trees, 3D-SPIHT)以及3D小波嵌入零块编码算法(3D set partitioned embedded bloCK, 3D-SPECK)。 但这些算法都无法解决因数据量急剧增加所带来的存储和传输压力。 现有的压缩加密算法， 没有根据多光谱图像的特点选择相对应的算法， 同时没有将压缩部分和加密部分紧密的结合在一起， 因此压缩加密效果欠佳。 针对多光谱图像的特点， 在参考KL变换最新技术以及最新压缩、 加密等算法[3-5]的基础上， 本文提出一种基于混沌与快速小波变换的多光谱图像压缩加密算法， 将压缩过程与加密过程紧密结合， 在提高图像存储、 传输效率的同时， 保证图像的安全性， 并实现了较高的压缩效率和较好的加密效果。

1 实验部分

1.1 多光谱图像压缩加密算法的设计

多光谱图像一般只有几个谱段， 是由二维的空间几何信息和一维的光谱信息组成的三维立体图像。 这种图像不仅存在空间相关性， 而且还有谱间相关性。 为了有效地去除空间相关性以及谱间相关性， 同时保证多光谱信息的安全性， 结合多光谱图像的光谱特性， 本文提出了如图1所示的结构：

首先将多光谱图像聚类为通用像素； 对通用像素进行二维离散9/7小波变换， 在空间方向上将能量变换成一系列系数， 消除多光谱图像大部分空间冗余， 减少压缩过程中的块效应； 然后对变换后的系数进行Arnold变换以及加密处理； 之后对产生的小波系数进行基于不同基的KL变换， 克服了单一KL变换基压缩性能有限的通病， 有效地保护了多光谱信息， 并实现了较高的压缩性能和压缩效率， 消除残余空间冗余和光谱冗余； 最后采用差分脉冲滤波器对系数进行编码， 并采用Tent映射对码流进行混淆扩散加密， 最后， 通过解压解密算法重建多光谱图像。

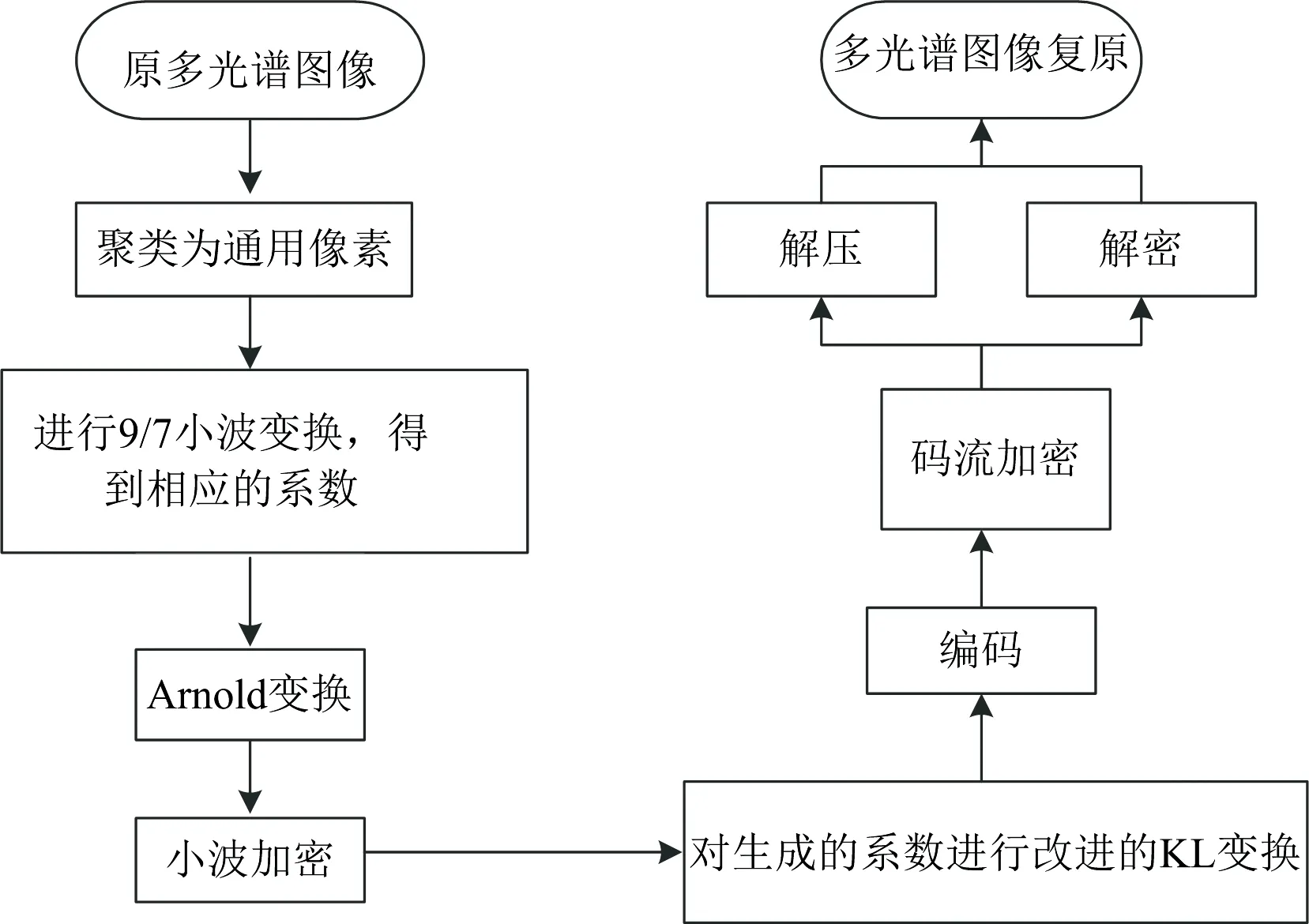
图1 多光谱图像压缩加密算法流程图

1.2 构造通用像素

超像素由一系列位置相邻且颜色、 亮度、 纹理等特征相似的像素点组成的小区域。 这些小区域大多保留了进一步进行图像分割的有效信息， 且一般不会破坏图像中物体的边界信息。 通用像素由具有全局视图的高维图像空间中最相似的像素组成， 跟超像素具有很多相似的属性， 是超像素的扩展。 不同之处在于， 超像素位于相连的邻域中， 通用像素不位于较小的局部区域。 通用像素可以表示为

(1)

式(1)中，I是多光谱图像的像素集，Ik={Ik, 1,Ik, 2,Ik, 3,…,Ik,nk(k=1, 2, …,K)}表示具有nk个像素的第k个通用像素，K是通用像素的数量，Da是通用像素中相似像素的阈值。 通用像素中的像素数直接影响算法的性能， 因此， 选择合适的K值非常重要。

本文采用K-means聚类方案来构建通用像素。 K-means算法按照样本之间距离大小， 将样本分为K个簇， 使簇间的距离尽量大， 簇内的点的距离尽量小。 多光谱图像像素之间的距离公式为

α×(‖Ib‖2-‖Ia‖2)

(2)

式(2)中，Ib，Ia是多光谱图像中任意两个像素， ‖·‖2表示向量的2范数， Dis(Ia,Ib)表示两个像素之间的距离。α是修正范数差异的平衡参数。 通过迭代的方法， 使目标的平方误差最小， 即

(3)

式(3)中，μi是簇Ci的均值向量。

1.3 小波加密算法

本加密算法由生成子密钥、 小波系数置乱和数据流加密3部分构成。

1.3.1 生成子密钥

本文采用的混沌系统为改进的Logistic映射和Tent映射， 改进后的映射方程为

xn+1=[μ0+(4-μ0)×cos((10-6+xn)×π/2)]×

xn×(1-xn/n)

(4)

(5)

其中，p∈(0, 1)，xn∈[0, 1]，μ0为3.569 945 673， 放大因子1/n∈(0, 1)。 当μ∈(3.569 945 673, 4]时， Logistic映射生成的序列处于混沌状态， 且当其取值为4时， 系统处于最佳混沌状态， 但此时的加密效果较差。 因此本文采用一个无限接近4的表达式代替4， 以达到预期的混沌特性以及安全性。

我们把通过Logistic映射构造散列函数生成的散列值分为5组， 记f1，f2，f3，f4和f5。 由式(6)生成子密钥， 作为Logistic映射的初始值。

(6)

式(6)中， mod表示模运算。 给定初始密钥x0，x1和x2， 由式(7)扰动初始密钥生成子密钥， 并分别作为Tent映射的初始值、 控制参数和初始密文块。

(7)

1.3.2 小波系数置乱

构造完通用像素后， 为了减少压缩过程中的块效应， 保护图像的真实信息， 需对像素进行小波变换。 小波变换是在傅里叶变换的基础上提出的一种新的变换方法， 在延续了短时傅里叶变换局部化优点的同时， 克服了傅里叶变换的一系列缺点。 下面将给出小波变换的基本概念。

如果函数满足容许性条件

(8)

二维小波函数可由一维小波的张量积构造， 二维连续小波变换为

WΨf(a,b,c)=∬f(x,y)Ψa, b, c(x,y)dxdy

(9)

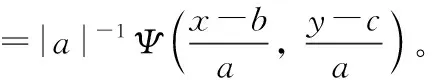
二维离散小波变换是在二维连续小波的基础上进行参数量化， 即：a=2-j，b=i12-j，c=i22-j，j，i1，i2∈Z，Ψj, i1, i2(m,n)=2jΨ(2jm-i1, 2jn-i2)， 可得信号的二维离散小波变换为

(10)

对图像进行一次小波变换， 将产生四个子带， 分别为低频子带(LL)， 水平方向高频子带(LH)， 垂直方向高频子带(HL)， 对角线方向高频子带(HH)。 二次变换是在低频子带(LL)的基础上重复类似的划分。 针对不同的子带系数进行不同的处理， 以达到更好的研究效果。

本文采用Arnold变换对小波变换后的系数进行置乱。 根据Arnold变换周期表， 选择合适的次数对目标像素进行变换置乱， 得到变换置乱图。

1.3.3 KL变换

KLT可用于主成分分析(principal component analysis, PCA)， 是一种具有去相关性能的线性可逆变换。 原算法计算过程如下：

首先， 将含有N谱段的多光谱图像矩阵采用行堆叠的方法整合成二维矩阵Y， 计算向量Y的平均值， 计算过程如式(11)所示。

(11)

其次， 求向量Y的协方差矩阵C， 计算过程如式(12)所示。

(12)

最后， 求协方差矩阵C的特征值和特征向量。 可得KL变换表达式如式(13)所示。

Y=AT(Y-m)

(13)

该算法所需运算量巨大， 其中计算M×N大小的谱段需要(M×N-1)次加法和1次除法， 计算H需要(M×N)次减法， 而其他步骤的运算所需的运算复杂度更高， 针对此问题， 将作如下改进。

首先， 计算协方差时并不使用全部光谱向量， 而是随机地选取光谱向量的一个子集， 适当选取该子集大小， 在保证图像质量的前提下尽量降低计算复杂度。 通过实验可得， 在采样后的尺寸为传统方法的1/100时， 压缩性能最好， 计算复杂度也较低， 综合考虑压缩性能与计算时间， 本文选用此值作为采样比估算协方差。

然后， 求对称矩阵特征值与特征向量时常采用Jacobi算法， 然而， 利用Jacobi算法求特征值不仅要选取主元素， 而且还要同时进行行与列的旋转变换， 使得整个计算的过程十分复杂， 难于并行实现。

最后， 计算特征向量矩阵。 代替经典KLT中的矩阵乘法(均值×特征向量)， 采用提升方案。 将特征向量矩阵分解为AT=PLUS， 其中P为置换矩阵，L为单位下三角矩阵，U为单位上三角矩阵，S为对角矩阵。 为了保持无浮点输出， 在每个阶段之后， 对输出元素进行舍入。 改进后的KL表达式如式(14)所示。

Y=round(round(round(XS)U)L)P

(14)

式(14)中， round表示四舍五入。 乘以P就是元素交换， 其中乘法仅由1和0进行。 因此， 置换并不是计算密集型的， 因为它只需要循环遍历向量就可以交换某些元素。S矩阵是稀疏的下三角矩阵； 因此， 通过将零校验技术应用于乘法运算， 可以需要更少的元素乘法运算。

变换后效果图见图2， 对一幅多光谱图像(含4个谱段)的前三个谱段(a， b， c)分别作KLT， 得到三幅变换后的图像(d， e， f)， 消除了大部分谱间冗余， 能量主要集中在前两个谱段。

图2 各个谱段KL变换效果图

1.3.4 数据流加密

为了进一步压缩， 需要将原始信号转换为新的整数流， 并将整数流转换为二进制编码流， 并采用霍夫曼编码。 但是， 如果这些整数通过霍夫曼编码直接转换为二进制比特流， 则也将需要太多的存储空间。 因此， 采用DPCM滤波器将原始信号转换为新的整数数组。

首先， 用量化器对非零系数统一进行量化。 然后， 为了节约存储空间， 进一步压缩非零系数， 我们将处理得到的系数， 使原始信号转换为新的整数数组。 最后， 将整数流转换成二进制编码流， 实现图像的高效编码。

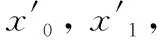
首先， 将R分成n个长度为32的子块m。

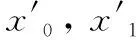
(15)

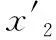
xi=SR[(mod((ri⊕mq+xi-1), 232),

(16)

2 结果与讨论

2.1 加密性能分析

2.1.1 抗攻击性分析

根据香农定理， 熵可以反映信息量的大小。 加密效果越好， 信息越混乱， 与此同时， 图像中所含的信息越少， 信息熵越大。 信息熵的计算公式如式(17)

(17)

式(17)中，pi为像素i出现的概率。 表1显示了几种加密算法的信息熵差异。

表1 信息熵对比

从表1中可以看出， 本算法的信息熵更接近理想值(12)， 具有更好的抗攻击性。

像素变化率(the number of pixels change rate， NPCR)和归一化平均变化强度(the unified average changing intensity， UACI)是有效分析抗差分攻击的重要指标。 其中NPCR表示不同密文图像在相同位置上灰度值互不相同的比率， UACI表示不同密文图像之间的平均变化密度。 其公式如式(18)和式(19)所示。

(18)

(19)

其中，m和n分别表示图像的行和列， 当C1(i,j)=C2(i,j)时D(i,j)=0， 反之，D(i,j)=1。 表2列出了本算法与其他几种算法的NPCR和UACI的测试结果。

表2 NPCR和UACI的测试结果

NPCR和UACI的值越大代表算法的抗差分攻击能力越强。 由表2可知， 本算法的NPCR和UACI优于现有算法， 因此， 与同类算法相比， 本算法可以更好的抵御差分攻击。

为进一步验证本算法加密效果， 选取多幅具有三个波段的多光谱图像进行加密前后的水平、 垂直以及对角线方向的相关系数进行测试， 测试结果(均值)见表3。

由表3可知， 经加密后， 图像的相关系数明显降低。

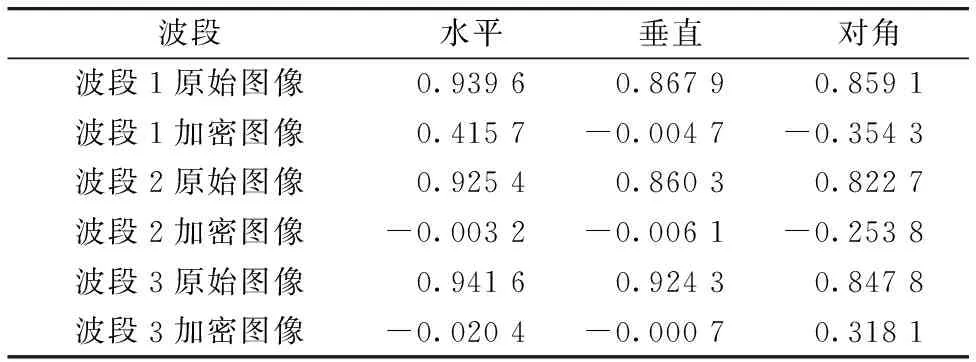
表3 加密前后相关性

本算法共5个初始密钥， 每个密钥产生的精度空间接近1016。 加密的过程中， 密钥随着明文的变化而不断变化。 因此， 该算法具有较大的密钥空间， 能有效抵抗已知明文攻击和穷举攻击。

2.1.2 加密敏感性分析

为了验证算法对密钥的敏感性， 采用具有微小差异的密钥对原图像加密， 比较码流的变化率。 通过实验可得， 输出比特流变化率保持在47.62%～47.71%之间， 具有较好的密钥敏感性。

保持密钥不变， 随机改变图像中某一像素值， 通过加密后的比特流变化评价本算法对明文的敏感性。 对具有不同特征的特定压缩比的QuickBird进行100次仿真实验， 通过实验可知， 密文比特流变化率保持在47.45%～47.52%。 由此可知， 本算法对明文图像很敏感， 可有效抵抗差分攻击。

为方便观察实验结果， 利用该算法对多光谱图像的某谱段进行加密， 加密效果如图3所示。 由图3可以看出， 本算法具有较好的加密效果， 有效地保护了多光谱图像的有用信息。

图3 某谱段图像与加密图像

同时， 本算法对多幅多光谱图像的不同谱段分别进行了测试， 均有较好的加密效果。

2.2 压缩性能分析

为方便验证算法的可行性， 测试图像选用具有三个谱段的多光谱图像。 整个算法在计算机上用Matlab R2012b进行仿真。 像素深度为8 bit/pixel(b/p)， 压缩比为16∶1， 实验结果如图4所示， 其中a为原始图像， b为重建后图像。

由图4可知， 在码率比较高的情况下， 本算法的PSNR特别高， 重构后的图像与原图像差别不大。 图像经DWT与KLT后， 大部分像素值位于1 bit， 可见， 光谱冗余被消除掉了。

为进一步验证压缩后图像的质量， 选择4组具有不同特征的QuickBird多光谱图像进行测试， 每组20幅， 并用最近提出的多光谱图像压缩算法进行比较。 测试结果见表4。

图4 原始图像与压缩重构图像对比图

由表4可知， 在4∶1～32∶1范围内， 本压缩算法达到很高的峰值信噪比， 优于现有的压缩算法， 在正常工作压缩比为16∶1时， 比现有压缩算法的信噪比提高了0.64 dB以上。 为进一步测试本算法的性能， 进行了极高压缩比条件下的测试。 在压缩比64∶1和128∶1的情况下， 系统的PSNR可分别达到35.03和31.28， 优于现有算法1 dB以上。 可见， 本算法可行， 且特别适合对压缩比要求较高的场合。

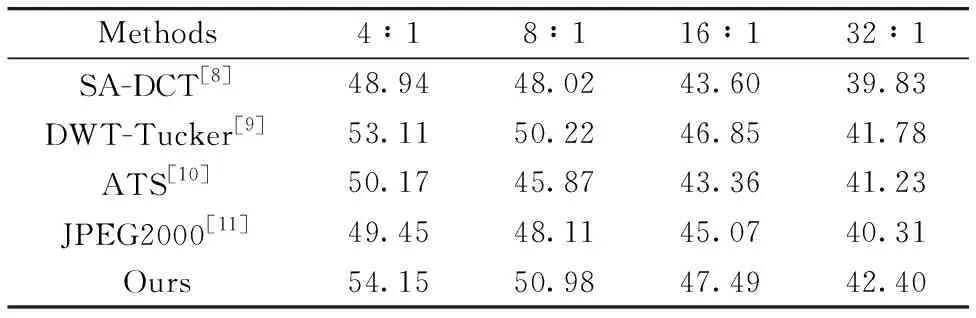
表4 压缩系统测试结果

表5列出了本算法与现有的一些算法的数据处理速度比较结果。 由表5可知， 本文提出的压缩算法数据吞吐率低于现有压缩算法， 与JPEG2000相比处理速度相当， 但压缩比要远远高于JPEG2000以及其他压缩算法。 本算法吞吐率略低的一部分原因是因为与其他压缩算法相比， 算法中加入了加密算法， 提高了算法的复杂度。 随着硬件方案的不断完善， 该算法的处理速度会不断提升， 与此同时算法的高峰值信噪比优势将更加明显。

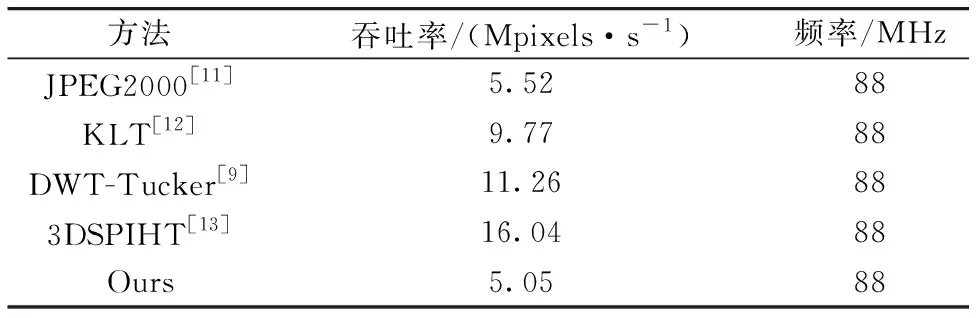
表5 数据处理速度比较结果

为验证算法的去冗余效果， 测试图像选用JPL实验室的AVIRIS多光谱图像序列。 多光谱图像经二维离散9/7小波变换后， 大部分空间冗余被消除了， 子带HL像素深度由8 bit减少到0～6 bit， 大部分像素值为5 bit左右。 经KL变换后， 大部分像素位于0.9 bit左右。 对图像采用信息熵进行比较， 经9/7小波变换后的图像信息熵为6.864 9， KL变换后图像的信息熵为3.015 8。 可见， 多光谱图像经小波变换和KL变换后， 空间冗余和光谱冗余大部分被消除了， 图像的压缩比得到了极大的提升。

与多光谱图像相比， 高光谱图像以及超光谱图像拥有更多的波段， 同时波段更加连续， 相邻波段高度相关， 因此其数据量更大、 冗余信息更多， 压缩加密的难度会有所提升， 但其冗余的特性相似。 本算法基于光谱图像的谱间冗余以及空间冗余特性进行压缩以及加密， 因此， 本算法同样适用于高光谱图像以及超光谱图像的压缩加密， 同时， 在此基础上进行了大量的测试， 测试效果较为理想。

原始像素和重建像素之间的光谱失真常用于测量保真度， 而光谱角距离(SAD)是评价多光谱图像的最常用的标准之一。 较小的SAD意味着压缩具有较少的信息损失， 并且重构的多光谱图像对于后续应用更为可靠。 为方便起见， 我们采用均值SAD来揭示多光谱图像的平均光谱失真。 关于不同方法的均值SAD的结果如图5所示。 从图中我们可以看到， 该方法在最大比特率下实现了较小的平均SAD， 这表明该方法的平均频谱失真小于其他方法。 因此， 所提出的方法具有良好的频谱保真度。

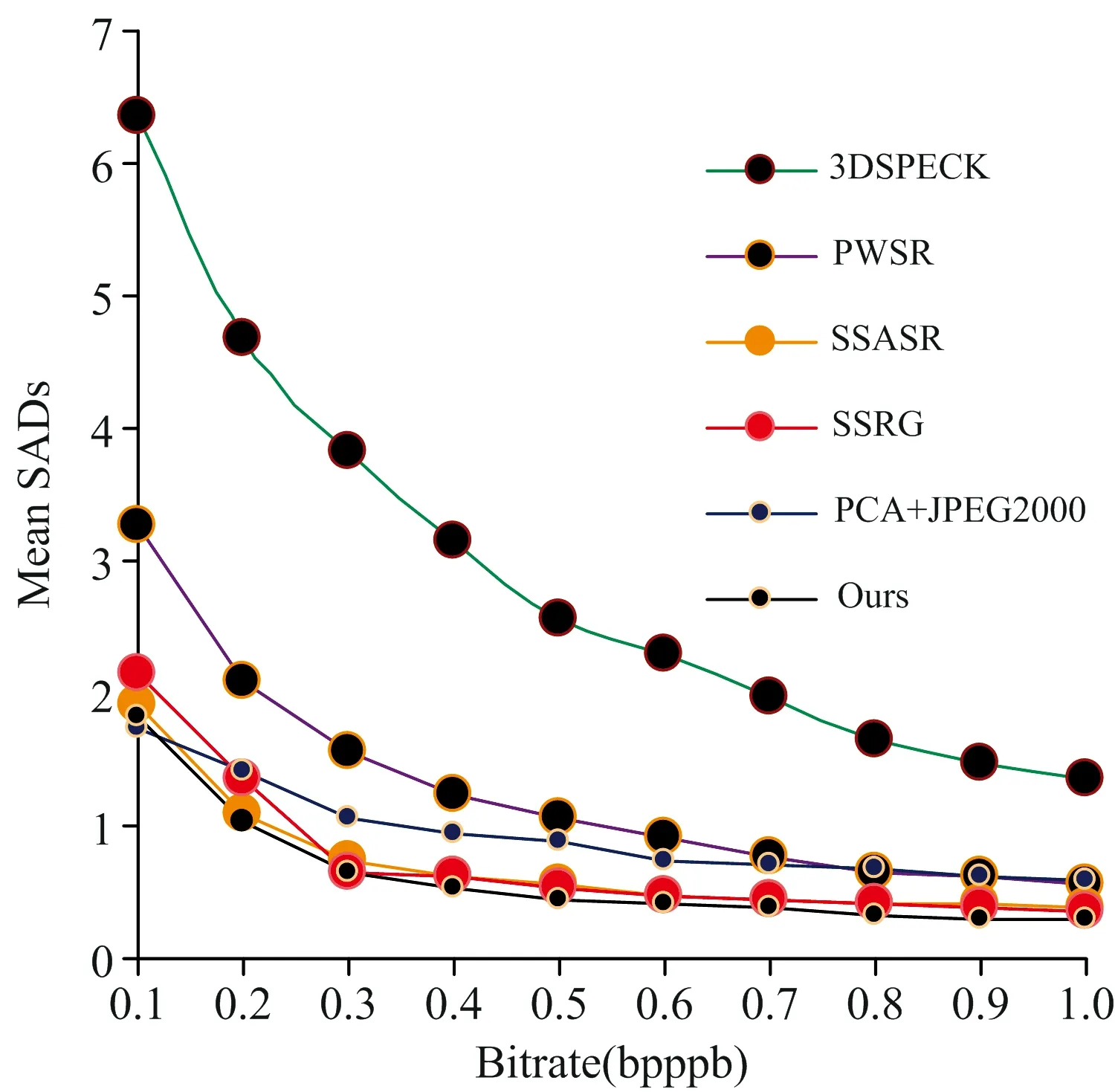
图5 均值SAD

3 结 论

多光谱图像在提供了关于地物更细致的光谱信息的同时， 其数据量急剧增加， 给机载和星载数据传输和存储带来困难。 此外， 由于某些侦察监视工作不希望被其他国家或者组织破解， 因此除了通信链路加密之外， 非常有必要对多光谱图像进行加密， 以确保数据的安全性。 在此基础上， 本文提出一种将混沌思想、 小波变换和KL变换相结合的多光谱图像压缩加密算法。 该算法充分利用多光谱图像的冗余特性， 弥补了传统算法的不足。 实验结果表明， 该方法信噪比高、 运算时间短、 密钥空间大， 同时对密钥和明文敏感， 并在频谱保真方面具有较好的效果。