刚竹毒蛾胁迫下毛竹叶绿素与叶光谱特征的关系及其变化

胡新宇, 许章华, 3, 5, 6*, 黄旭影, 8， 张艺伟， 陈秋霞，王 琳， 刘 辉， 刘智才

1. 福州大学环境与安全工程学院， 福建 福州 350108 2. 福建省资源环境监测与可持续经营利用重点实验室， 福建 三明 365004 3. 空间数据挖掘与信息共享教育部重点实验室, 福建 福州 350108 4. 福州中谷海创科技发展有限公司， 福建 福州 350108 5. 福州大学先进制造学院， 福建 泉州 362200 6. 福州大学信息与通信工程博士后科研流动站， 福建 福州 350108 7. 福建农林大学公共管理学院， 福建 福州 350002 8. 南京大学国际地球系统科学研究所， 江苏 南京 210023

引 言

据估算， 全球竹林总面积为30 538.35×103hm2[1]。 全国第九次森林资源清查显示， 我国有竹林面积逾640万hm2， 竹子种类和竹林面积稳居全球首位。 毛竹具有根系密集、 生长周期短、 经济与生态价值高等特点， 是我国重要经济竹种， 竹产业年产值已超2 000亿元， 成为许多地区践行习近平总书记“绿水青山就是金山银山”理念、 助力乡村振兴的重要资源保障。 然而， 虫害一直威胁着竹林健康， 并呈现种类多、 致损严重的态势， 导致林分质量下降， 竹林价值受损。 其中， 刚竹毒蛾是我国竹林最主要的一种食叶性害虫， 具有群发性、 周期性、 危害极严重等特征， 广泛分布于福建、 江西、 浙江等多个省区。 叶绿素含量是绿色植物生长状态的重要评价指标， 是评价植物光合作用能力、 监测生长环境优劣、 判断植物生理营养是否充足的重要依据。 叶绿素含量监测主要可采用分光光度计、 荧光或活体叶绿素仪等进行测定[2]， 但这些方法效率偏低并可能影响植物的正常生长， 同时也难以全面掌握林分的整体状态。 高光谱技术为叶绿素的定量化监测提供了一种简便有效且破坏度较小的途径， 相比于多光谱， 其对光谱信息的细化也为深入探索植被叶绿素变化规律提供了重要基础。 Sonobe等[3]发现， 采用预处理技术与机器学习结合的方式对两种山葵叶绿素含量估测获得较好效果； 韩浩坤等[4]在RVI， PSNDb， GNDVI750的基础上建立了糜子冠层叶绿素含量的高光谱反射率模型； Zhang等[5]发现反射率一阶微分值构建的多元回归方程以及修正的绿色归一化植被指数对雷竹叶片叶绿素的拟合效果较好。

虫害侵染是植被叶绿素等理化参数发生改变的重要诱因， 反之叶绿素也可作为植被健康状况的主要判定依据之一。 在农林病虫害领域， Souza等[6]等通过衡量叶绿素a在除草剂胁迫下的荧光特征值分析玉米基因是否受草地夜蛾危害的影响； 有报道采用叶绿素与含水量特征， 将松材线虫害分为5种等级， 并采用光谱特征参数构建了光谱特征模型； 王景旭等[7]通过实验发现随着切梢小蠹的侵入时间延长， 叶绿素含量呈现先平缓后急剧的下降趋势； 有研究选取包含相对叶绿素含量在内的理化参数作为因子， 对刚竹毒蛾危害进行了检测； 窦志国等[8]分析了健康和虫害芦苇叶片高光谱反射率与叶绿素含量间的相关关系， 建立了叶绿素含量红边位置和全波段高光谱反演估算模型； 周晓等[9]以二龄稻纵卷叶螟幼虫为试验材料， 分析不同投虫量条件下、 不同生育期水稻冠层的原始光谱、 三边参数和SPAD(soil and plant analyzer development)值的变化规律， 建立了水稻叶绿素相对含量的回归估算模型。

已有研究多着眼于改进算法并利用光谱信息估测植被叶绿素含量， 或者仅探索虫害发生前后叶绿素含量的变化。 尽管上述研究已较为丰富， 关于虫害胁迫下叶光谱信息与叶绿素含量的变化机理却鲜有涉及。 刚竹毒蛾作为威胁毛竹林健康、 制约竹产业高质量与可持续发展的主要因素， 探索其虫害发生发展与叶绿素、 叶光谱特征关系具有重要意义。 研究从地面非成像高光谱数据入手， 分析并筛选了4种高光谱指标， 基于4种回归模型构建不同致损状态下毛竹叶片叶绿素含量估测模型， 分析比较基于不同刚竹毒蛾危害等级下SPAD与毛竹叶光谱特征关系， 为进一步深入探索刚竹毒蛾虫害响应与毛竹叶片理化参数变化研究奠定基础。

1 实验部分

1.1 野外调查与毛竹叶片样本采集

试验区位于福建省南平市顺昌县， 地理坐标为117°29′—118°14′E， 26°38′～27°12′N[图1(a—c)]。 顺昌县为亚热带海洋性季风气候， 干湿季明显， 森林资源丰富， 是我国南方的重点林区， 有“中国竹子之乡”的美誉。 截至2018年底， 全县林地面积达16.7万hm2， 其中竹林面积为4.4万hm2， 毛竹立竹量1.1亿根。 长期以来， 刚竹毒蛾均是威胁该县毛竹生长的主要食叶型害虫， 严重制约竹林健康与竹林产业可持续发展。 据2019年顺昌县林业有害生物统计数据， 该县当年刚竹毒蛾发生面积为1.34万hm2， 约占全县竹林面积的1/3。

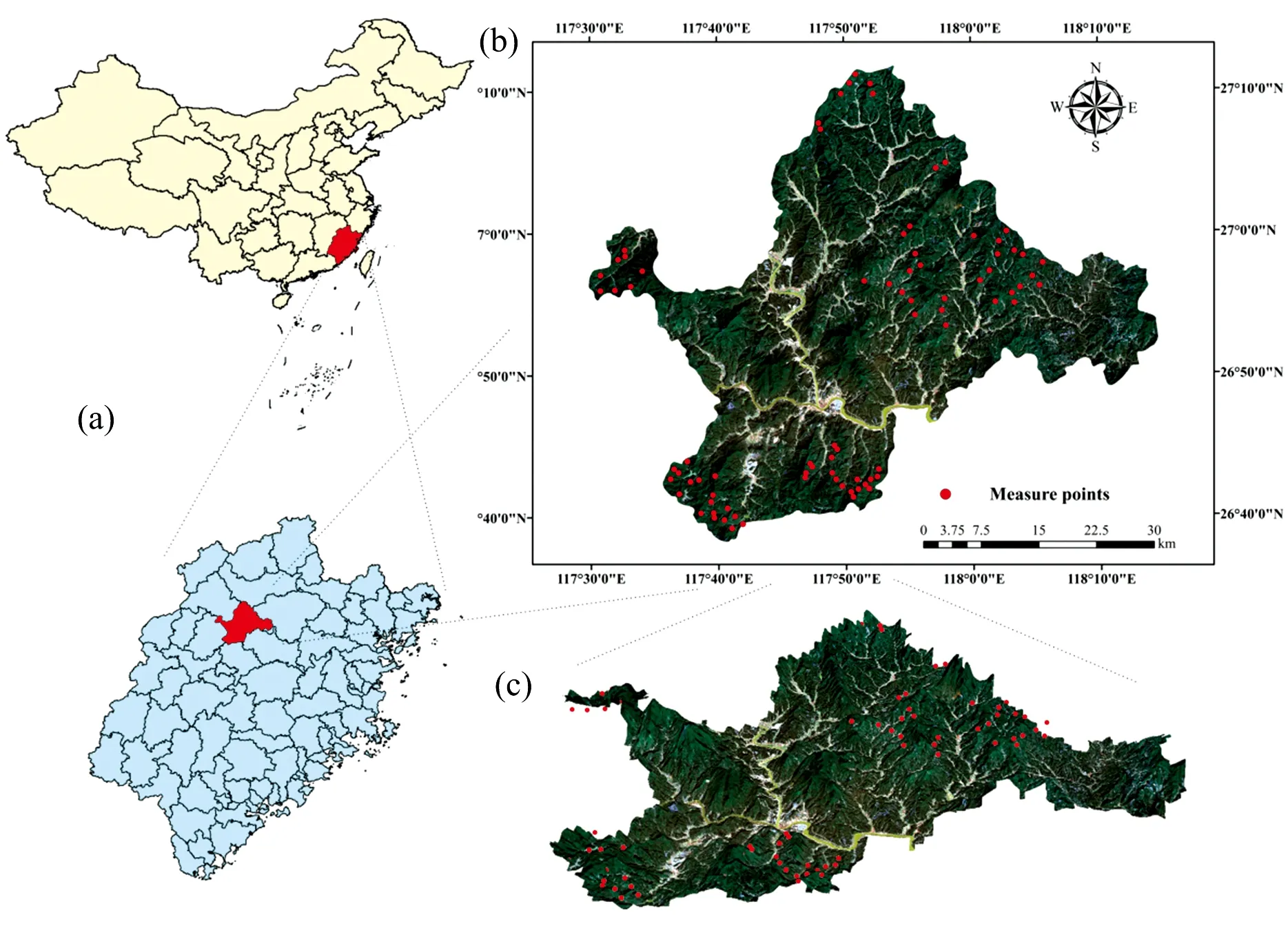
图1 顺昌县地理区位图(a)、 研究区遥感影像测量点2D影像(b)和3D影像(c)

刚竹毒蛾的年生代数因地而异， 福建省多为3代。 课题组于2020年7月—9月(刚竹毒蛾第二代)赴试验区， 以小班为单位开展现场踏查。 通过随机采样的方式， 于不同林样地中采集不同竹龄及健康程度的毛竹叶片样本。 不同于林分尺度依靠虫株率、 虫口数量/密度的方法， 本文叶片尺度危害等级的确定采用综合判定法： (1)根据刚竹毒蛾的危害机制以及国家林业局发布的《林业有害生物发生及成灾标准》， 将单株失叶率(健康： 0%、 轻度危害： 0～25%、 中度危害： 25%～50%、 重度危害： >50%)及虫口数量(健康： <10条、 轻度危害： 10～30条、 中度危害： 31～80、 重度危害： >80条)列入危害等级划分的参考因子。 除此之外， 因毛竹林养分的制造、 积累、 分配、 消耗不平衡的周期变化， 使得毛竹出笋、 成竹年和换叶年交替进行， 故毛竹林也分为大小年。 根据竹林历年的出笋、 成竹平均数作为划分大小年的临界判别值， 高于或等于该值即为大年， 小于该值即为小年。 处于小年期的毛竹会显示出落叶、 枯黄等特征， 小年阶段毛竹处于换叶期， 营养用于竹鞭生长， 其外部形态与虫害叶片类似但受虫害影响较少， 故若不对其加以区分则会对毛竹叶片光谱信息收集及叶绿素含量测定工作造成极大干扰。 本研究划分危害等级的叶片均于大年毛竹林中采集， 并额外采集了部分小年毛竹叶片作为参照； (2)以植物保护、 森林保护等学科背景的高校学者及长期从事森防检疫工作的林业从业人员为对象， 采用专家咨询法对危害等级进行最终判定。

1.2 毛竹叶绿素与叶光谱数据的获取

课题组于试验区使用日本Mioolta公司生产的美能达牌SPAD-502P叶绿素计对毛竹叶片叶绿素含量快速无损监测， 通过测量叶片的吸收率， 得到的数据应与叶片内部结构的叶绿素浓度成正比， 通常情况下叶片叶绿素浓度的相对值即为SPAD值。 每叶片于叶尖、 叶中、 叶基处测得3个SPAD值， 取其平均值作为该叶片的SPAD值。

叶片光谱数据利用ASD Field Spec4 HandHeld光谱仪(Analytical Spectral Device， US)及配套的植物光谱探测器(Unit 16558 plant probe)获取， 该仪器的波长范围为350～2 500 nm， 光谱分辨率为1.4 nm(350～1 000 nm)和1.1 nm(1 001～2 500 nm)， 重采样间隔为1 nm， 共有2 151个波段。 为确保光谱数据的准确性， 每隔20 min进行一次白板校正。 每片叶子在黑色背景下测量其10次正面光谱， 在该仪器配套的光谱处理软件(View Spec Pro)环境下剔除异常值后取光谱数据的平均值作为样本实测光谱数据。 根据研究需要， 采用The Unscrambler X10.4软件中的Savizky-Golay卷积平滑算法对原始光谱进行预处理， 截选400～2 000 nm光谱数据予以统计。

1.3 毛竹叶光谱特征指标计算与关系模型建立

1.3.1 特征光谱

高光谱数据波段数较多， 波段信息冗余且复杂。 为了更有效地识别筛选目标地物， 节约计算成本， 采用连续投影算法(successive projection algorithm， SPA)提取特征光谱信息。 该算法是一种前向循环的特征变量选择算法， 利用向量的投影分析， 选取含有最低冗余度和最小共线性的有效波长， 对光谱波长进行优选， 减少建模所需变量个数， 改善建模条件。 该算法步骤如下：

(1) 在光谱矩阵中任选一条光谱列向量作为起始向量；

(2) 分别计算剩余列向量在起始向量的正交平面上的投影向量；

(3) 挑选出最大的投影作为下一次投影的起始向量， 直到挑选变量个数达到最大所需个数；

(4) 将提取的所有波长组合进行多元线性回归， 最小的均方根误差(RMSE)所对应组合即为最优的波长组合。

经过上述步骤筛选出特征波长为469， 702和760 nm， RMSE为0.062 4。

有研究表明， 高光谱衍生指标与叶绿素含量之间的估测模型是叶绿素变化检测研究的有效途径。 因此， 除原始特征光谱外， 本研究选取植被指数、 光谱微分、 红边参数3种高光谱衍生指标以期更清晰全面地探究毛竹叶片叶绿素与叶光谱特征之间的关系。

1.3.2 植被指数

植被指数类型众多， 部分研究显示[10-11]， 叶光谱指数与SPAD之间的经验模型可有效估算叶绿素含量。 根据应用尺度的不同， 可以分为叶片尺度和冠层尺度两类光谱指数。 叶片尺度上应用的植被指数结构相对简单， 常用的类型主要有比值型(SR)、 差值型(D)、 归一化差值型(ND)、 新二重差值型(DDn)改进版本等。 除使用原始光谱构建光谱指数外， 也可使用一阶微分光谱构建光谱指数(可消除基线漂移和平缓背景干扰的影响， 并且可以放大光谱曲线中的细微变化)[12]。 所选取20种植被指数作为特征因子， 既包括基于传统多光谱数据所构建的宽带指数， 如适用于浓密植被的RVI与描述土壤-植被系统的SAVI等； 亦包括较宽带指数更为灵敏的窄带指数， 如对叶冠层微小变化敏感的NDVI705与对叶绿素浓度敏感度较高的VOG系列指数等[13-21]。 本工作选取典型高光谱植被指数(表1)应用于毛竹叶片叶绿素含量的反演研究。

1.3.3 光谱微分

经过微分处理的光谱数据不仅能消除基线漂移和背景干扰的影响， 还可以放大光谱曲线中的细微变化， 提供比原始光谱更高分辨率、 更高清晰度的光谱轮廓。 一阶微分光谱可更好地表示原始光谱数据的变化率和极值点， 二阶微分则突出了光谱曲线中切线斜率的变化速度。 计算公式如下

(1)

(2)

式(1)和式(2)中， FDRλi为波段i和波段i+1之间的一阶微分光谱值； SDRλi为波段i和i+1之间的二阶微分光谱值；λi为第i波段的波长值；Rλi+2，Rλi+1，Rλi分别代表λi+2，λi+1，λi波段处的原始光谱反射率； Δλ代表波段λi+1到λi之间的波长差值。 下文使用469FDR， 469SDR分别代表469 nm处一阶微分光谱值与二阶微分光谱值， 其他特征波长处同。

1.3.4 红边参数

红边参数可指示植物的健康状况， 在病虫害检测方面有重要作用， 常见的有叶绿素吸收比值指数(chlorophyll absorption ratio index， CARI)、 红边斜率(red edge slope， RES)、 红边面积(red edge area， REA)、 红边差值植被指数(red edge difference vegetation index， REDVI)、 红边比值植被指数(red edge ratio index， RERVI)、 红边归一化差值植被指数(red edge normalized difference vegetation index， RENDVI)， 计算公式分别为

b=ρ550-550a

即红边覆盖680～780 nm范围内一阶微分光谱的最大值。

表1 叶绿素相关植被指数

即红边覆盖680～780 nm范围内一阶微分光谱的总和。

REDVI=ρ780-ρ680

1.3.5 关系模型构建原理

采用多算法构建比较毛竹叶绿素与叶光谱特征的关系模型， 探究在传统回归模型与机器学习回归模型下， 所选特征是否可有效模拟叶绿素含量与叶光谱特征关系。 综上所述， 采用多元线性回归、 岭回归、 随机森林回归、 XGBoost回归4种模型对毛竹叶片SPAD进行拟合。 通过对比4种模型的优劣确定SPAD为最佳估测模型， 基于模型估测结果分析不同危害程度下毛竹叶片叶绿素含量与叶片光谱特征关系。

(1)多元线性回归： 是多元回归分析中最基础、 最简单的一种， 即一个样本中有多个特征的线性回归问题， 对于一个有n个特征的样本i而言， 其回归结果如式(3)

(3)

式(3)中，w被统称为模型的参数， 其中w0为截距(intercept)，w1～wn为回归系数(regression coeffcient)。

(2)岭回归： 又称为吉洪诺夫正则化(Tikhonov regulation)， 是一种专用于共线性数据分析的有偏估计回归方法， 是在多元线性回归的损失函数上加上了正则项， 通过放弃最小二乘法的无偏性， 以损失部分信息、 降低精度为代价获得回归系数， 使结果更符合实际。 该算法不是为了提升模型表现， 而是为了修复漏洞所设计。

(3)随机森林： 是一种典型的Bagging集成算法， 其所有基评估器都是决策树， 回归树所集成的森林即为随机森林回归器(图2)。 其优势在于对数据集的适应能力强， 具有很好的抗噪性能和极强的拟合能力但是不会产生过拟合现象[22]。

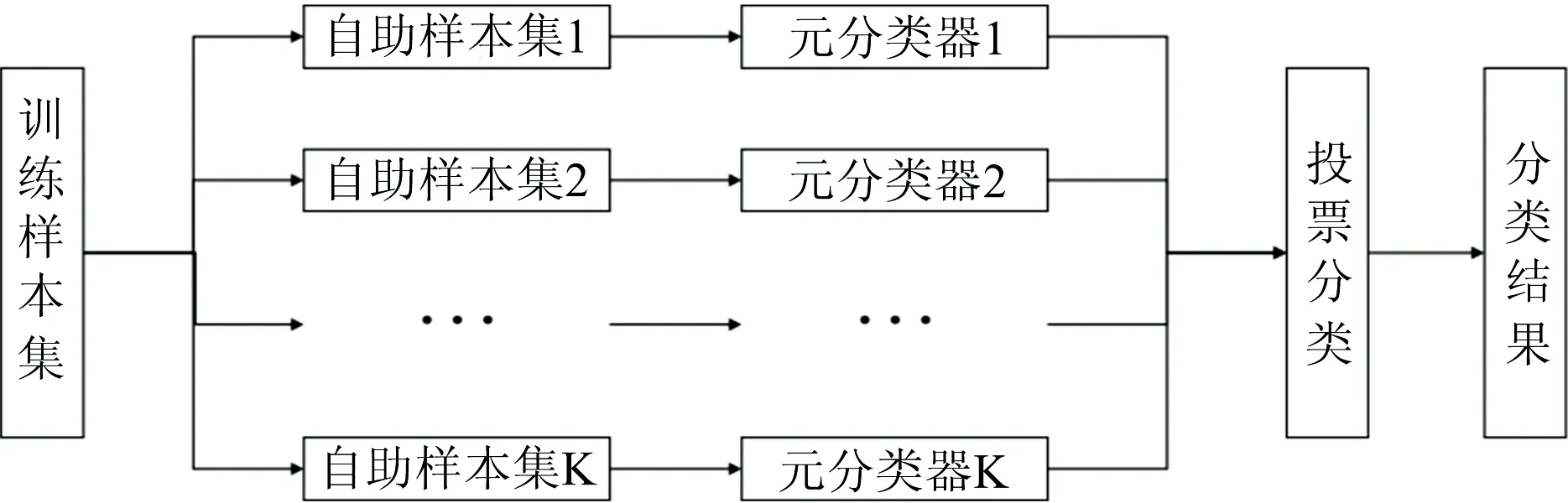
图2 随机森林结构图

(4)XGBoost(extreme gradient boosting)： 是在GBDT(gradient boosting decision tree)的基础上改进的一种Boosting模型， 凭借其可扩展性强， 运行速度快等优势， 在机器学习和数据挖掘领域中有着深远的影响。 与随机森林不同的是， XGBoost的决策树建立过程是根据算法中线建立的决策树情况而定， 而随机森林中决策树的建立是相互独立的， 每颗子树为一个弱分类器[23]。 具体目标函数如式(4)和式(5)

(4)

(5)

式(4)和式(5)中，T为叶子节点的个数， ‖W‖为叶子节点向量的模，γ表示节点切分的难度，λ表示L2正则化系数。

本实验选取370片毛竹叶片样本， 经判定各危害等级叶片数量为无危害： 83、 轻度危害： 71、 中度危害： 70、 重度危害： 89、 小年： 57。 将其中70%作为训练集(样本容量为259)， 30%作为测试集(样本容量为111)代入4个模型之中进行评估。

2 结果与讨论

2.1 毛竹叶绿素含量变化分析

刚竹毒蛾作为典型食叶性害虫威胁毛竹林健康， 主要通过侵蚀叶片影响毛竹叶绿素含量， 使植物叶片组织发生改变， 光合作用减少进而改变毛竹叶片光谱吸收特征。 图3显示了全体叶片样本、 不同危害等级及小年情况下毛竹叶片样本SPAD的变化情况。 当刚竹毒蛾虫害初发时， 毛竹叶中的各种营养成分含量尚未出现明显变化； 随着失叶程度的不断加重， 竹体的养分循环系统被完全破坏， 由此导致其中的养分元素含量产生显著变化， 进而出现病斑、 枯萎等症状， 此时毛竹叶片样本SPAD值整体呈现下降的趋势。

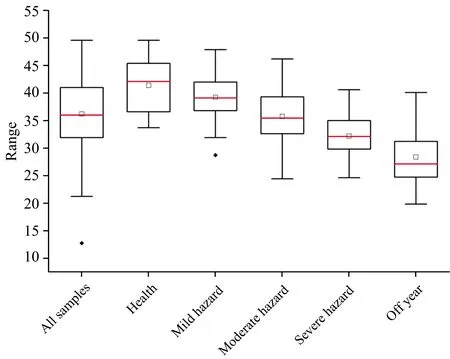
图3 不同状态下毛竹叶片样本SPAD变化趋势

2.2 毛竹叶光谱特征变化分析

毛竹叶片的光谱曲线存在极为明显的峰谷特征， 这与大部分绿色植被的光谱特性基本一致。 当刚竹毒蛾危害发生时， 失叶状态下的寄主会产生失绿、 缺水等病症， 其光谱特征随即产生显著变化[图4(a,b)]， 具体表现为： (1)健康竹叶在520～570 nm波长范围内因叶绿素吸收较少而形成了一个绿色波段的小反射峰， 称之为“绿峰”。 (2)在640～700 nm波长范围因叶绿素的强吸收形成了一个红色波段吸收谷， 称之为“红谷”。 由于叶片的多孔薄壁细胞结构特性对近红外光强烈的反射， 形成光谱上的最高峰。 (3)当毛竹遭受虫害侵蚀后光谱发生明显变化， 主要表现为可见光波段范围内的“绿峰”和“红谷”逐渐消失， “红边”斜率减小， 近红外波长反射率降低。 随着虫害程度加重， 这一现象更加明显。 导致这一现象发生的主要原因是毛竹遭受虫害侵蚀后， 竹叶叶绿素含量相对减少， 细胞结构遭到破坏。 因此， 根据光谱间的差异， 进行竹叶叶绿素含量的估算是可行的。

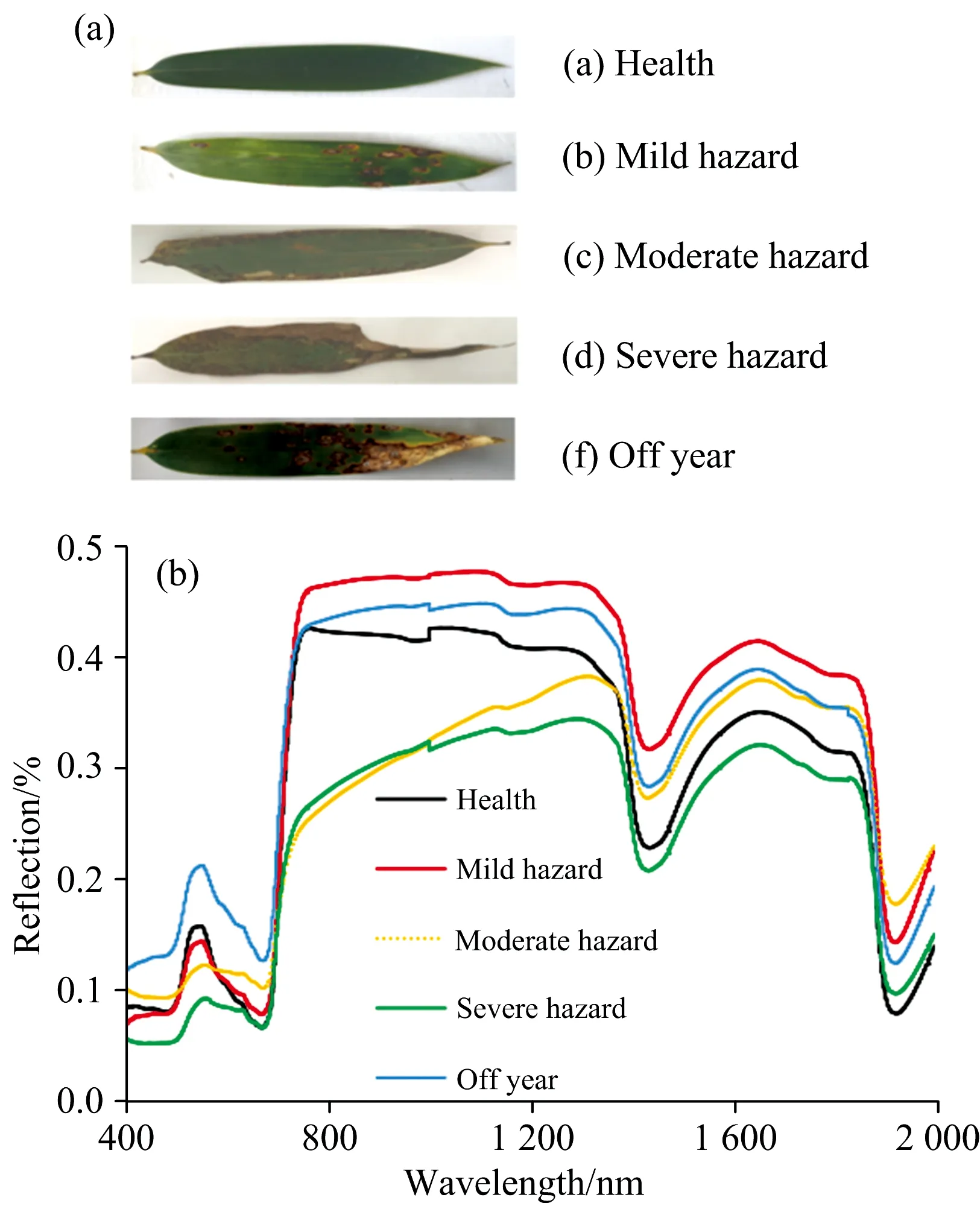
图4 不同状态下的毛竹叶片样本(a)及其光谱信息(b)

相比之下， 小年叶片和健康叶片的光谱差异更为明显。 在可见光—近红外波段范围内， 小年叶片的反射率总体上高于健康及受害叶片； 至短波红外波段区间， 其反射率虽仍高于健康叶片， 但与受害叶片的差异并不算太明显， 虽然在1 450及1 940 nm波段上， 各健康状态叶片依然会呈现出一定的规律， 但总体而言， 小年叶片的识别研究重点应该落在可见光-近红外范围内。

2.3 关系模型特征指标筛选分析

2.3.1 基于全样本的叶光谱特征指标筛选分析

用于反演叶绿素的特征指标众多， 为减少计算量， 避免造成实验结果冗余、 复杂， 需首先对上述植被指数进行筛选。 Pearson相关系数， 是一种线性相关系数， 通常用来度量两个变量X和Y之间的相互关系， 其计算公式为[24]

(6)

式(6)中， Cov(X,Y)代表X与Y的协方差， Var(X)和Var(Y)分别表示X和Y的方差。 当相关系数为1时，X与Y的关系为Y=aX+b，a>0； 当相关性为-1时，X和Y的关系为Y=aX+b，a<0。 如果X和Y相互独立， 相关系数为0(图3、 图4)。 本研究中将毛竹叶SPAD作为变量X， 将叶光谱特征指标作为变量Y进行Pearson相关分析。

图5显示， 植被指数对毛竹叶片SPAD的响应最为显著。 依照Pearson相关系数从大到小排列， 有5种植被指数的Pearson相关系数较为突出， 分别为： VOG2(-0.651**)，R515/R570(0.643**)， CIred(0.607**)， PRI(0.606**)及NDVI705(0.606**)， 故将上述5个植被指数作为SPAD估测毛竹叶片全体样本SPAD模型的特征指标。 而通过分析特征光谱与光谱微分， 可以发现在469和702 nm处原始光谱对SPAD的相关性较高， 而在760 nm处， 光谱微分则呈现较为明显的相关性。 红边参数RES， REA， REDVI与SPAD的相关性较高而CARI， RERVI， RENDVI却呈现较低的相关性。

图5 全体叶片样本叶光谱特征指标Pearson相关分析

2.3.2 考虑不同危害等级的叶光谱特征指标筛选分析

对全体叶片样本划分危害等级与小年叶片， 再次进行Pearson相关分析， 结果如图6(a—e)所示。

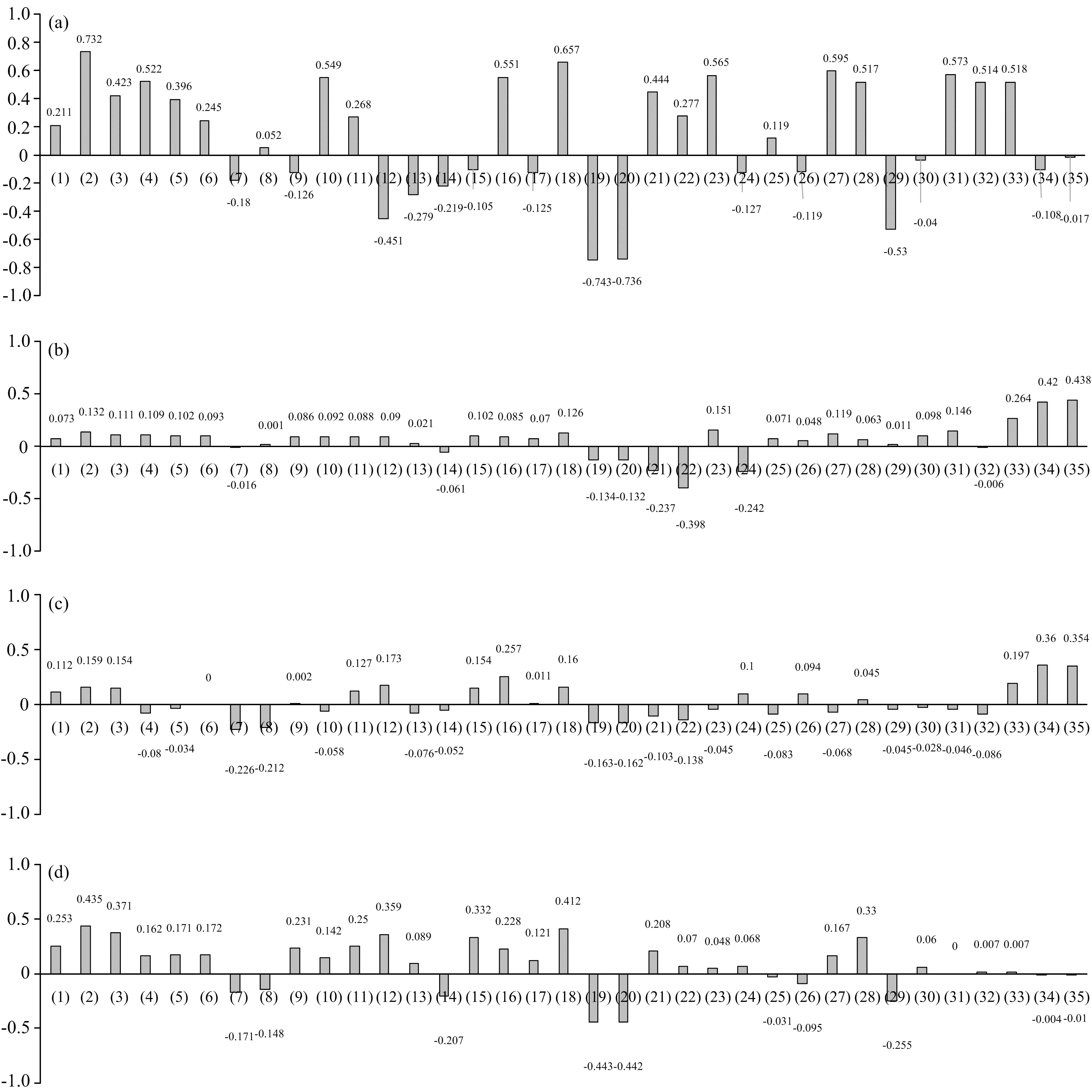
图6 不同危害等级下叶片样本叶光谱特征指标Pearson相关分析

不同致损状态下的毛竹叶片， 呈现趋势为健康状态及小年叶片样本相关性较佳的特征指标较多， 而与轻度、 中度及重度危害叶片样本相关性较佳的特征指标较少， 具体表现为： 与健康状态的毛竹叶片相关性较佳的植被指数有： CIred(0.732**)， VOG2(-0.743**)， ARVI(0.549**)，R515/R570(0.551**)， DVI(0.522**)； 与小年毛竹叶片相关性较佳的植被指数有： PRI(0.706**)， NDVI705(0.704**)， VOG1(0.696**)， CIred(0.65**)。 与轻度、 中度危害叶片样本SPAD相关性较高的指标主要集中于红边参数， 与轻度虫害相关的指标有： RENDVI(0.438**)， RERVI(0.42**)及REDVI(0.264*)； 与中度虫害相关的指标与轻度虫害相同， 其Pearson相关系数分别为： RENDVI(0.354**)， RERVI(0.36**)及REDVI(0.197*)； 与重度虫害的毛竹叶片相关性较佳的植被指数有： VOG2(-0.443**)， CIred(0.435**)， NDVI705(0.371**)， PRI(0.359**)。 据此将上述指标代入模型进行计算。

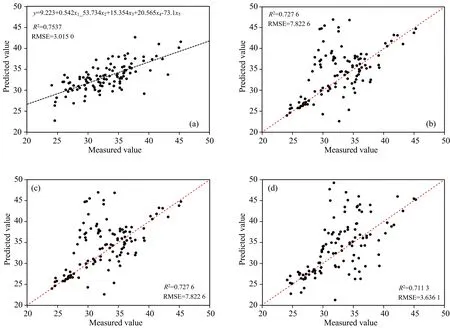
图7 4种模型对毛竹叶片SPAD检测结果(R2与RMSE分别为模型拟合度与均方根误差， 下同)

2.4 叶绿素与叶光谱特征模型构建与关系分析

2.4.1 基于全样本的模型构建及叶绿素、 叶光谱关系分析

将上述选取的特征指标分别代入多元线性回归、 岭回归、 随机森林及XGBoost 4种回归模型之中， 以特征指标作为自变量， SPAD作为因变量对全部叶片样本进行叶绿素估测， 模型评价指标为拟合度(R2)及均方根误差(root mean square error， RMSE)[图7(a—d)]。 其中岭回归正则化参数α=0.01； 随机森林回归部分重要参数的调参结果为： random_state=90， n_estimators=141， max_depth=12， min_samples_split=5， min_samples_leaf=2， max_features=9； XGBoost部分重要参数的调参结果为： random_state=420， obj=reg: linear， max_depth=1， eta=0.02， gamma=50， nfold=4， lambda=1， alpha=0， colsample_bytree=1， colsample_bylevel=1， colsample_bynode=1。

从上述模型估测结果中， 可以发现基于总叶片样本环境下多元线性回归模型对SPAD的检测结果最佳，R2为0.753 7， RMSE为3.015 0， 其拟合方程为式(7)

SPAD=9.223+0.542×NDVI705+53.734×PRI+15.35×CIred+20.565×R515/R570+73.1×VOG2

(7)

XGBoost对SPAD的拟合结果较差，R2为0.711 3， RMSE为3.636 1。 值得注意的是， 岭回归及随机森林的RMSE均较高， 分别为7.456 0与7.822 6， 说明这两种模型对于SPAD的检测较为不稳定。 综合上述结果， 无法清晰地看出毛竹叶SPAD与叶光谱特征的关系， 故本研究对全体样本进行危害等级及小年叶片划分， 以求探究在不同危害等级下， 叶光谱关系模型估测结果发生何种变化。

2.4.2 考虑不同危害等级的模型构建及叶绿素、 叶光谱关系分析

根据2.1中的特征指标筛选结果， 将CIred， VOG2， ARVI，R515/R570， DVI作为健康叶片的特征指标， RENDVI， RERVI， REDVI作为轻度危害及中度危害叶片的特征指标， VOG2， CIred， NDVI705， PRI作为重度危害叶片的特征指标， PRI， NDVI705， VOG1， CIred作为小年叶片的特征指标。 将上述特征指标分别代入多元线性回归模型、 岭回归模型、 随机森林回归模型及XGBoosting回归模型， 结果分别如图8(a—t)所示。

图8 4种模型对不同危害等级下毛竹叶片SPAD检测结果

基于不同危害等级下对比上述模型的检测结果， 主要有以下几点特征： (1)分析模型R2， 多元线性回归模型的检测效果要优于其他模型， 不同危害等级多元线性回归的R2分别为健康叶片： 0.882 3、 轻度虫害： 0.180 2、 中度虫害： 0.360 4、 重度虫害： 0.467 7、 小年叶片： 0.732 4； (2)分析模型RMSE， 多元线性回归模型亦普遍较为稳定， 不同危害等级多元线性回归的RMSE分别为健康叶片： 1.638 8、 轻度虫害： 3.335 4、 中度虫害： 3.886 7、 重度虫害： 2.601 8、 小年叶片： 2.375 4。 综合判断， 多元回归分析可较好地估测小年及健康叶片SPAD， 对于轻度-中度-重度危害叶片的估测效果较差。

估测健康叶片的回归方程为式(8)

SPAD健=-31.839+16.005×CIred+11.833×VOG2+49.892A×RVI+92.883×R515/R570+339.104×DVI

(8)

估测小年叶片的回归方程为式(9)

SPAD小=40.049+9.036×PRI-21.091×NDVI705+27.81×VOG1+76.019×CIred

(9)

2.5 虫害胁迫下毛竹叶SPAD关系模型的不确定性原因

为分析出现SPAD关系模型结果变化原因， 对毛竹叶片样本进行讨论。 图9显示了不同危害等级下叶片样本在3种高光谱特征指标构成的特征空间中的分布情况， 健康叶片与小年叶片样本主要集中于右上视面与左上视面， 而轻度危害-中度危害-重度危害样本则较为离散地分布于特征空间中， 这表明健康与小年状态下的叶片叶光谱特征较为明显， 而其他危害等级下的叶片在所选取的高光谱特征指标中表现不突出， 故上述研究中3种危害等级叶片在Pearson相关分析中所表现出的相关性较差， 同时4种模型对其估测结果也较低。

图9 全体叶片样本及不同危害等级下叶片样本叶光谱指标特征空间

2.6 毛竹叶绿素估测模型结果分析

叶绿素是毛竹个体中参与光合作用的重要色素， 其通过捕捉光能转变为化学能用于毛竹个体的生长和代谢。 叶绿素含量的高低可直接反映毛竹的生境状况， 而虫害胁迫下致使毛竹叶片生境及理化参数改变已成为阻碍估测毛竹叶片叶绿素含量的重要因素。 因此， 研究如何快速且准确估测毛竹叶绿素含量及解析其与叶光谱特征关系变化具有重要意义。 本研究首先分析了不同危害等级毛竹叶片的划分依据， 在此基础上对全体叶片样本及不同危害等级下的毛竹叶片进行叶光谱特征指标筛选， 再将筛选的指标代入4种模型中。 由此发现， 多元线性回归模型对全体毛竹叶片样本SPAD具有较好的估测能力， 而针对不同危害等级下的叶片样本， 模型的估测效果也随之发生改变。 究其原因主要有以下两方面：

首先， 无论特征指标和叶片致损状态如何变化， 岭回归和多元线性回归的检测结果总是十分接近， 并保留相同的变化趋势。 事实上， 通过选取不同的正则化参数α， 发现当α趋于更小值时， 岭回归的决定系数R2也更加趋近于多元线性回归(图10)。 这是因为岭回归是对多重共线性问题进行回归分析的一种统计方法， 是在多元线性回归的损失函数上加上了正则项， 表达为ω的L2范式乘以正则化系数α， 其损失函数的完整表达式写作式(10)

(10)

假设特征矩阵结构为(m,n)， 系数ω的结构是(1,n)， 则有

(XTX+αI)ω-XTy

(11)

式(11)中， RSS为残差平方和，I为结构为n×n的单位矩阵。 假设原本的特征矩阵中存在共线性， 则方阵XTX就会不满秩。 对于存在“高度相关关系”的矩阵， 可以通过调大α控制参数向量ω的偏移， 即模型越不容易受到共线性的影响。 因此若一个数据集于岭回归中使用各种正则化参数取值下模型表现没有明显上升， 则说明数据没有多重共线性， 反之亦然。

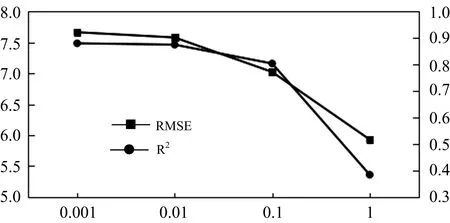
图10 不同正则化参数下模型R2及RMSE变化

针对随机森林回归模型与XGBoost回归模型， 尽管通过调参缩小了模型的过拟合问题， 但过拟合现象仍然存在。 本研究中所涉及的数据量较少且数值变化较为稳定， 无法很好发挥出随机森林与XGBoost模型的优势， 故在本研究中估测精度较多元回归分析略低。

2.7 虫害与毛竹叶片叶绿素及叶光谱特征关系分析

当刚竹毒蛾危害发生时， 其幼虫食出的缺刻使竹叶中的水分迅速流失， 导致叶绿素的合成速率下降。 随着危害程度的不断加剧， 残余竹叶中的水分及叶绿素含量不断降低， 进而影响其光合效率。 由于植被吸收的能量通常比用于光合作用的能量更多， 其自身的各种光保护机制使植被能够释放存在潜在威胁的多余能量。 但当光合效率减弱到一定程度时， 光能吸收-释放的平衡被打破， 过多的能量将导致致命的感光氧化。 与此同时， 光合效率减弱进一步导致竹体内的水分无法被有效耗解， 由此引发恶性循环， 竹节内逐渐产生积水， 而竹冠则不断干枯。 因此， 选择可反映以上表征变化的指标是确定其虫害胁迫程度的关键。 本研究从原始光谱、 植被指数、 红边参数及光谱微分4个光谱特征指标入手， 从多角度指示毛竹SPAD在不同危害程度下叶光谱特征的变化差异， 由此发现， 随着虫害程度的加重， 叶光谱特征指标的相关性呈现显著下降趋势， 致使模型对存在虫害胁迫的叶片SPAD估测效果不佳。 可见， 当毛竹叶SPAD与叶光谱特征的关系趋向紊乱时， 可预示虫害发生。

3 结 论

基于实测毛竹叶片样本SPAD及叶光谱数据， 采用Pearson相关法对不同危害等级下毛竹叶片SPAD的高光谱衍生指标进行筛选， 据此代入多元线性回归、 岭回归、 随机森林回归及XGBoost 回归4种模型中对毛竹叶片SPAD信息予以估测， 基于模型估测指标分析叶绿素与叶光谱特征关系变化， 得出以下结论：

(1)随着虫害程度的加剧， SPAD普遍呈现下降的趋势。

(2)虫害胁迫下叶光谱特征发生明显变化， 其可见光波段范围内的“绿峰”和红谷逐渐消失， “红边”斜率减小， 近红外波长反射率降低。

(3)基于总样本， 根据Pearson相关法筛选出估测全体叶片样本SPAD的最佳指标为： VOG2(-0.651**)，R515/R570(0.643**)， CIred(0.607**)， PRI(0.606**)及NDVI705(0.606**)。 依据上述指标拟合出的最佳模型为多元线性回归模型，R2为0.753 7， RMSE为3.015 0， 其拟合方程为： SPAD=9.223+0.542NDVI705+53.734PRI+15.35CIred+20.565R515/R570+73.1VOG2。

(4)基于不同危害等级下的叶片样本， 多元回归模型是最佳估测模型， 随着危害等级变化多元线性回归的估测效果也随之改变， 分别为， 健康叶片：R2=0.882 3， RMSE=1.638 8； 轻度虫害叶片：R2=0.180 2， RMSE=3.335 4； 中度虫害叶片：R2=0.360 4， RMSE=3.886 7； 重度虫害叶片：R2=0.467 7， RMSE=2.601 8； 小年叶片：R2=0.732 4， RMSE=2.375 4。 可以看出， 模型对于健康叶片与小年叶片的SPAD估测效果较好； 对于轻度危害—中度危害—重度危害叶片的SPAD估测效果较差。

(5)通过构建由不同叶光谱特征组成的特征空间， 分析不同危害等级下叶光谱特征关系不确定的原因， 为小年与健康叶片样本SPAD较为集中地分布在特征空间中的不同视面， 而其他危害等级叶片样本的SPAD则呈现较为离散地分布， 致使样本特征不够突出。

综上所述， 通过本方法所选取的敏感性指标并利用多元线性回归模型进行计算， 对毛竹叶片SPAD具有良好的估测效果， 而通过分析叶光谱特征与虫害发生关系， 则可发现在不同危害等级下光谱特征表征也随之改变， 同时基于不同危害等级亦可发现当毛竹叶SPAD与叶光谱特征的关系趋向紊乱时， 则预示着虫害的发生。 本研究可为毛竹健康监测及其刚竹毒蛾危害响应与预警研究提供理论支持。