Impact assessment of the seasonal hydrological loading on geodetic movement and seismicity in Nepal Himalaya using GRACE and GNSS measurements
2022-09-05DevenrShshikntNgleSureshKnnujiyPrmGutmAjyTloorTnrilSrkr
Devenr Shshiknt Ngle ,Suresh Knnujiy ,*,Prm K.Gutm ,Ajy K.Tloor ,Tnril Srkr
a Indian Institute of Remote Sensing, ISRO, Dehradun, Uttarakhand 248001, India
b Wadia Institute of Himalayan Geology, Dehradun, Uttarakhand 248001, India
c Department of Remote Sensing and GIS, University of Jammu, Jammu 180006, India
d Indian Institute of Technology (Indian School of Mines), Dhanbad 826004, India
Keywords:Non-tectonic Terrestrial water storage GRACE Strain rate Seismicity
ABSTRACT The Himalayan terrain is an epitome of ongoing convergence and geodetic deformation where both tectonic and non-tectonic forces prevail. In this study, the Gravity Recovery and Climate Experiment(GRACE) and Global Positioning System (GPS) datasets are used to assess the impact of seasonal loading on deformation with seismicity in Nepal. The recorded GPS data from 21 Global Navigation Satellite System(GNSS)stations during 2017-2020 are processed with respect to ITRF14 and the Indian reference frame, and the Center for Space Research (CSR) mascon RL06 during 2002-2020 is adopted to estimate the terrestrial water storage(TWS)change over the Ganga-Brahmaputra River basin.The results indicate that the hydrological loading effect or TWS change shows high negative, high positive, and moderately positive values in pre-monsoon, co-monsoon, and post-monsoon months, respectively. The detrended GPS data of both horizontal and vertical components correlate with the seasonal TWS change using the Pearson correlation coefficient at each GNSS site. In addition, the correlation coefficient has been interpolated using inverse distance weighting to investigate the regional TWS influence on geodetic displacement. In the north component, the correlation coefficient ranges from -0.6 to 0.6. At the same time,the TWS is positively correlated with geodetic displacement(0.82)in the east component,and the correlation coefficient is negative(-0.69)in the vertical component.The negative correlation signifies an inverse relationship between seasonal TWS variation and geodetic displacements. The strain rate is estimated, which shows higher negative values in pre-monsoon than in post-monsoon. Similarly, the effect of seismicity is 47.90% for pre-monsoon, 15.97% for co-monsoon, and 17.56% for post-monsoon.Thus we can infer that the seismicity decreases with the increase of seasonal hydrological loading.Furthermore,the effect of strain is much higher in pre-monsoon than in post-monsoon since the impact of co-monsoon continues to persist on a small scale in the post-monsoon season.
1. Introduction
The collision of Indian and Eurasian plates about 65 million years ago gave birth to the Himalayas,considered to be one of the youngest orogenies on Earth[1].The upliftment and subsidence of the Plate depend on natural and anthropogenic activities [2].Several researchers observed that tedious accretion of interseismic strain resulted in several earthquakes up to MW8 [3-5].Earth is an elastic body that shows deformation on the surface when there is a mass change by atmospheric loading, terrestrial water storage loading, and non-tidal ocean loading [2,6]. The recent geodetic deformation in the Himalayas is majorly affected by surface hydrology [7]. For instance, in the south of Tibet and South India, signals of hydrological loading associated with tectonic movement are quite strong [8-11]. However, seasonal hydrological loading is a non-tectonic component that influences deformations [12]. The seasonal fluctuation effect is comparatively high in the post-monsoonal months (winter seismicity)than in the pre-monsoonal (summer seismicity) period. The periodic displacements of the lithosphere can be attributed to seasonal hydrological mass movement.GPS datasets are mainly used to monitor different seasonal deformation modes globally and understand the relation between active tectonic regions of strain accumulation [13].
During the summer monsoon(June-September),the Himalayas restrict the northern monsoon and increase the moist air aloft,which later cools down to lower temperatures. As a result, high rainfall intensity occurs on the southern side of the Himalayans.In addition, the annual melting of snow and glaciers significantly contributes to the seasonal hydrological loading.
Some studies have pointed out the possible reasons for the seasonal strain variation in Himalayan terrain [14,15]. One is that the creeping rate of main Himalayan thrust (MHT) induces interseismic shortening, which varies with time due to resonance with seasonal forcing. And the other is that the creep rate of MHT is constant, but the seasonal loading leads to stress variations that modulate geodetic strain and seismicity [16]. The earthquakes of high magnitude in the Nepal Himalayan region were quite intense,mainly due to the thrust events induced by N-S compression associated with the prevailing convergence[17].
To understand differences in pre-, co- and post-monsoon, the study uses data from the GRACE satellite, which is a twin satellite designed to study the Earth's gravity change and provide crucial information about the mass distribution on the crust.
The estimation of TWS has been carried out successfully in different areas globally[18].After removing atmospheric and oceanic parameters as well as geophysical causes, the GRACE data measure the Earth's gravitational variability with high accuracy[19].
Through GPS and GRACE satellites, we can measure the Earth surface displacement and terrestrial water storage, respectively[7,20-22]. The hydrological loading varies seasonally and corresponds to the vertical deformation rate in Himalaya, i.e., as the hydrological loading increases, the deformation rate increases[8,23-25].The high elevation of the Himalayas obstructs the southwest monsoon from the Indian Ocean, leading to intense precipitation, and this seasonal water mass is redistributed to Himalayan rivers such as Ganga and Brahmaputra.This redistribution implies crustal deformation in the central Himalayas and surrounding regions [23]. At the Himalayan arc, the convergence rate is about 20 mm/year[9,10].The elastic strain accumulation and convergence in the Himalayan region are prominent as measured by GPS [11].Seasonal change in hydrological loading results in an annual stress variation, which further leads to the micro-seismic earthquake in the main Himalayan thrust by strain accumulation [23,26-28].Studies have shown that vertical crustal deformation (VCD) is a significant parameter that can be estimated through space geodetic techniques.The VCD has been used to assess the seasonal variation of water storage since 2000 [29]. On the other hand, the water storage estimated from GRACE can be converted using VCD and then compared with the measurements inferred from GPS.Furthermore,when a well-connected GPS network exists,GPS VCD is regarded as a viable water storage option, especially in water balancing.The following equation shows that the water storage(S)is linearly related to VCD.

where Sgis the spatially weighted average of the n gridding at the GPS station g. The parameters α (slope), β (offset) can be determined by the least-square for converting VCD in the conversion to S. Therefore, the value of α must be negative when loading/unloading occurs at S, which leads to downward/upward movement in VCD [30].
Although there is some correlation between the seasonal hydrological loading time-series and historic earthquakes [12,31], its relation is still not fully understood[32].This study focuses on the effect of seasonal hydrological loading variation on geodetic deformation and seismicity in Nepal Himalaya.
2. Geology and seismotectonics
Nepal is located in the central part of the Himalayas, which occupies one-third of the 2400 km long range.Nepal is divided into six major tectonic zones from south to north,i.e.,the Gangetic Plain,Sub-Himalaya Zone,Upper Siwalik,Lesser Himalayan Zone,Higher Himalayan zone, and Tibetan-Tethys Zone [33].
As shown in Fig. 1, the Main Frontal Thrust (MFT), Main Boundary Thrust (MBT), and Main Central Thrust (MCT) converge to form the Main Himalayan Thrust (MHT) [34]. Continuous underthrusting of the Indian Plate has produced this thrust system,rejuvenating towards the south [35,36]. The MHT shows flat and sloping geometry [37], the shallower part is slipping episodically while the deeper part is creeping very smoothly[38].It is reported that the 1905 Kangra earthquake and 1934 Bihar-Nepal earthquake occurred due to the release of interseismic strain accumulated at the transition zone between the locked and creeping zones[39-43].2015 Nepal MW7.8 earthquake with a source at a depth of~15 km was ~77 km away from Kathmandu [34]. The earthquake and aftershocks originated from the flat part of MHT.According to the earthquake cycle model [44], future earthquakes (MW8) are likely to occur in this region.
3. Data and methodology
3.1. GPS data analysis for site velocity measurement with respect to ITRF2014 and Indian fixed reference frame
The central part of Nepal is one of the most seismically active areas globally. To study the geodetic displacement of this region, a total of 21 Continuously Operating Reference Stations(CORSs)have been selected. These stations are equipped with Leica/Trimble receivers and choke-ring geodetic antenna, of which the elevation angle is maintained under 10°. The data sampling time is around 30 s.GPS data from these stations during 2017-2020 were acquired in Receiver Independent Exchange Format(RINEX),which is further processed in GAMIT/GLOBK software(vs.10.71)[5,45,46].
GPS data processing includes two steps.The first is the GAMIT module,which estimates the relative positioning of the individual site with respect to satellites by using precise information. The information is provided by the satellite orbital parameters and clock errors, as well as the predicted error caused by ocean-tidal atmospheric water vapour and ionospheric electron content effect. The Finite Element solution (FES) 2010 model and International Earth Rotation System (IERS) 2010 model are used for reducing the ocean tidal and Earth tidal effects. And the Global Mapping Function (GMF) based on the Global Pressure Temperature(GPT)model is used to correct the tropospheric delay induced by wet and dry water mass[47].The second is the GLOBK module that analyzes the loosely constrained solutions and estimates the site velocity in ITRF14 after removing the transient or temporary deformation. The site velocity is also estimated from the Euler pole (Indian fixed reference frame) as suggested by [48] (Fig.1).After processing the periodic seasonal variations (annual and semi-annual) in the GPS time series using MATLAB software, the velocity rates were calculated for 21 stations(Fig.2).The seasonal signals are generally approximated as a linear combination of sine and cosine functions, indicating periodic perturbations [49,50].

Fig.1. The geological structures of the study area. MFT: Main Frontal Thrust; MBT: Main Boundary Thrust; MCT: Main Central Thrust.
3.2. GRACE derived terrestrial water storage (TWS) fluctuation in pre-, co- and post-monsoonal months
The study focuses on seasonal changes, i.e., the pre-, co-, and post-monsoon (Fig. 3). The pre-monsoon consists of March, April,and May; the co-monsoon includes July, August, and September;and the post-monsoon consists of October, November, and December.The monthly GRACE datasets from the Center for Space Research (CSR) during 2002-2020 were used in this study.
The TWS is estimated using the mass concentration blocks(mascons) approach. Implementing geophysical constraints is more accessible and rigorous in mascons [51]. The native resolution of CSR mascon RL06 is 1°× 1°represented on a ¼ degree longitude-latitude grid. These solutions are computed using regularisation constraints derived from GRACE/GRACE-FO satellite information. Tikhonov regularization and L-ribbon approach are used to estimate the regularization parameter, and no additional empirical de-stripping, filtering or smoothing is required here. The anomalies are relative to the mean baseline of 2004-2009, and the solutions are corrected with respect to ellipsoidal Earth[52].These corrections are separately carried out for land and ocean to prevent leakage in signals. Mascons parameters are geodesic tile elements used to estimate mass correction globally, with the rate of mass change expressed in centimeters of equivalent water height (uniform water mass layer). The mascon formulation is as follows [53]:

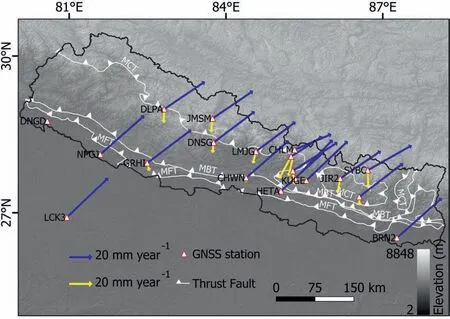
Fig. 2. The geological structures of the study area with GNSS station distribution. The triangle, blue vector, and yellow vector indicate the GNSS station, the velocity rates in International Terrestrial Reference Frame 2014 and India fixed frame, respectively.

Fig. 3. The (a) pre-, (b) co- and (c) post-monsoonal average map of TWS variation over South Asia during 2002-2020. Highlighted area shows the TWS fluctuation in the Ganga-Brahmaputra river basin. TWS is estimated based on CSR mascon data from GRACE and GRACE-FO satellites.
where y is a missing value between the two end variables,y1,y2,x1and x2are known end variables. The missing data between June 2017 and June 2018 were not interpolated,since this period was the gap between the GRACE and GRACE-FO mission. In all the calculations, this period was skipped.
The averages of pre-,co and post-monsoon TWS were obtained.We can find that the region where the Ganga-Brahmaputra River meets the Bay of Bengal shows the highest TWS in co-monsoon.All further calculations were performed using TWS data of highlighted portion in Fig.3.In this paper,the GRACE data were obtained over the Ganga-Brahmaputra River basin to study the TWS change or hydrological loading effect in different seasons.
3.3. Strain rate estimation with respect to IISC GNSS station and seasonal variation of seismicity
The baseline method is useful for estimating the strain between two stations[60].For calculating the strain,it is needed to estimate the baseline length between the two selected stations.We use the Haversine formula to calculate the baseline length[61],which is as follows:

where L1is the initial baseline length and L2is the final baseline length.
In this study,we used IISC as the base station(fixed)to estimate the strain(Fig.4).The baseline length of the previous year is taken as the initial length(L1),while the following year's baseline length is taken as the final length (L2).

Fig. 4. Average seasonal strain at GNSS stations showing high (negative) strain values in pre and post-monsoon season during 2017-2020.
Initially,the strain is calculated seasonally for every year during 2017-2020. The average of each season is expressed in a nanostrain unit. A bar graph of seasonal strain and GRACE-derived TWS is plotted to study the seasonal strain rate variation (Fig. 5).It shows that the strain rate is higher in pre- and post-monsoon than in co-monsoon.
Fig.6 shows the seasonal earthquakes and their locations during 1991-2021. The earthquake occurrence rate is 47.90%,15.97% and 17.56% in pre-, co- and post-monsoon. Due to a sudden change in temperature from monsoon to winter,there is still some monsoon influence after the post-monsoon,so the incidence of earthquakes is relatively lower in the summer.
We plotted the number of earthquakes seasonally related to GRACE-derived TWS to establish a relationship between them during 2003-2020 (Fig. 7). In the pre-monsoon, the number of earthquakes increases.

Fig. 5. Seasonal strain variation at GNSS stations with GRACE-derived TWS fluctuations.
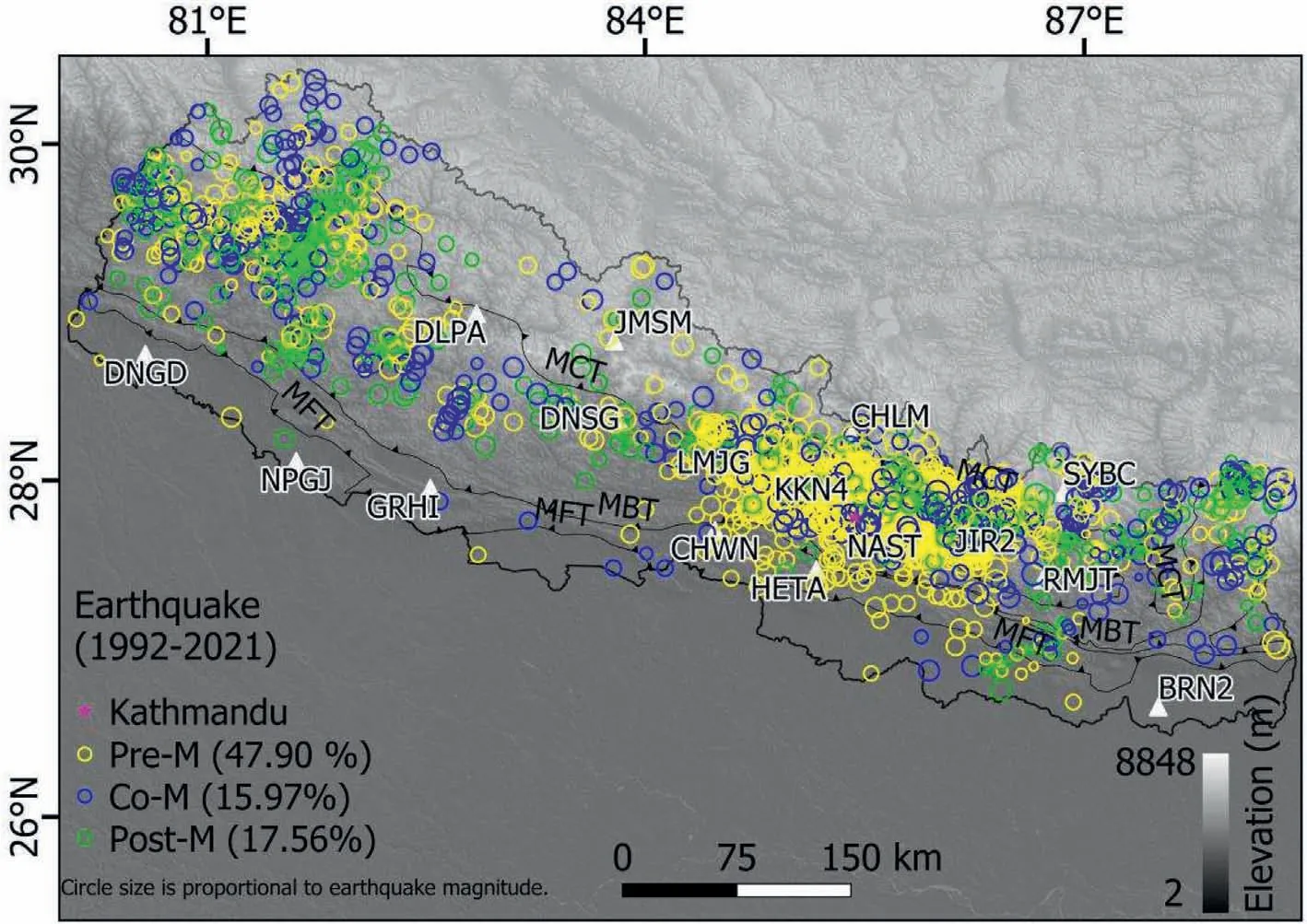
Fig. 6. Seasonal occurrence and spatial distribution of earthquakes during 1992-2021 (from ISC catalog).

Fig. 7. The number of earthquakes that occurred seasonally with GRACE-derived TWS fluctuations.
3.4. Correlation coefficient between GRACE-derived TWS and GPS data
We calculated the correlation coefficient at every GNSS station using Pearson's equation (Eq. (7)) to study the change in geodetic displacement due to seasonal TWS variation (Table 1).

After calculating the correlation coefficient at each point, we interpolated the correlation values using the inverse distance weighting(IDW)equation[62].Fig.8 shows the regional effect of seasonal TWS variation/hydrological loading on geodetic displacement. The negative relationship between TWS and geodetic displacement dominates in the vertical component,whereas the positive relationship dominates in the east component.

4. Results and discussions
4.1. The site velocity measurements
Higher velocities(ITRF14)are observed at stations in the higher Himalayas or the Indo-Gangetic plain (Fig. 3). For instance, the velocity at BRN2 is 52.42 mm/yr,while the velocity is 34.85 mm/yr at CHLM.This might be due to the higher crustal shortening in the northern part of the thrust system [63]. In addition, the velocities(Indian frame)are also higher in the Higher Himalayas.The velocity of the SYBC station (located near MCT) is 15.08 mm/yr, and the velocity at CHWN is 3.76 mm/yr.It might be due to the deformationof the plate boundary and the active thrusting of the Indian Plate beneath the Eurasian Plate. Table 2 depicts a high seasonal effect over the horizontal component than the vertical component.
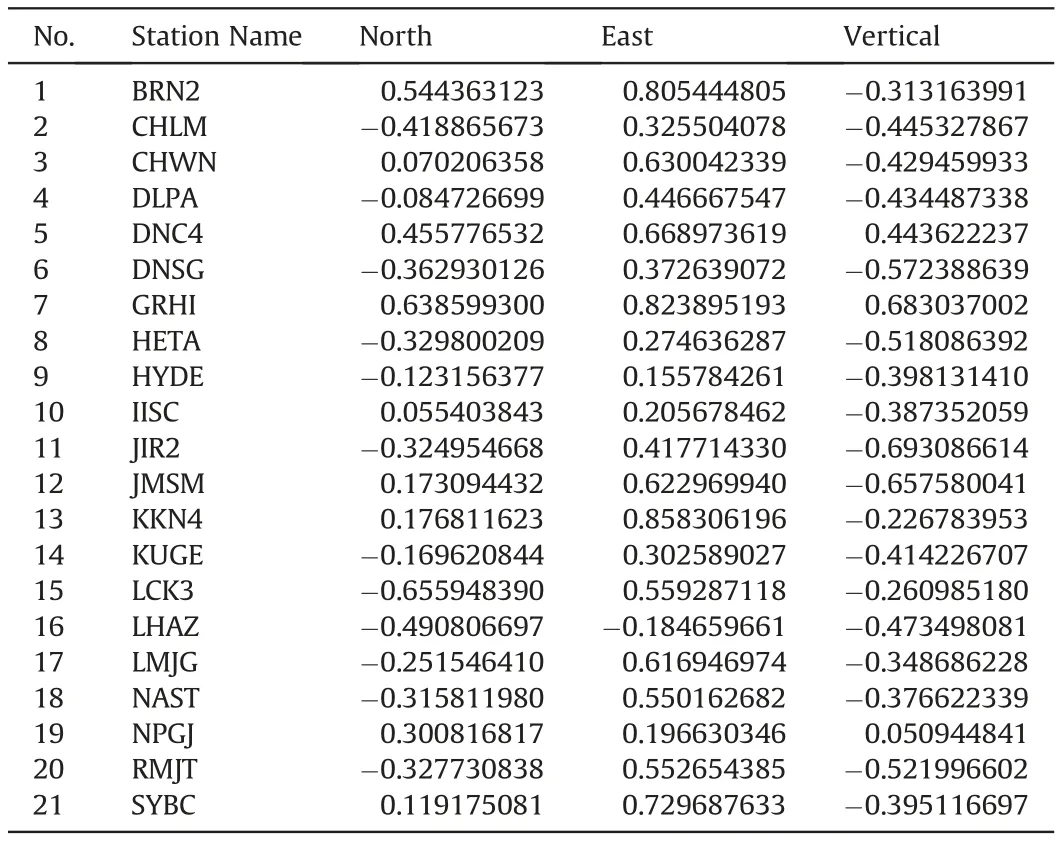
Table 1 Correlation coefficient estimated between hydrological loading and geodetic displacement of each GNSS station in north, east, and vertical components.
4.2. Terrestrial water storage change in pre-, co-, and postmonsoon months and its correlation with the geodetic displacement
The seasonal variation of TWS depends on the rainfall in the Ganga-Brahmaputra river basin for a particular year (Fig. 3). We estimated the seasonal interannual TWS variation during 2002-2020. The depletion of TWS shows high negative values(-54 cm) in the pre-monsoon period, mainly in the northwestern region. When the rainfall intensity increases in co-monsoon, the TWS variation exhibits high positive values (31 cm), mainly in the eastern-central part of Nepal and the southern part of India.During the post-monsoon, the TWS variation gives moderate values(-54-31 cm), highlighted by the blue-green color covering almost the whole study area.
Since TWS variation affects the geodetic displacement, we established the best correlation coefficient to investigate the hydrological loading impact on geodesy (Table 1). The vertical component shows negative correlation coefficients in all stations except GRHI and NPGJ. In the horizontal component, geodetic displacements show a negative correlation (-0.65 ~-0.08) with TWS at 12 sites(CHLM,DLPA,DNSG,HETA,HYDE,JIR2,KUGE,LCK3,LHAZ, LMJG, NAST, RMJT) and the remaining sites exhibit positive values(0.63-0.05).In the east component,geodetic displacements show positive correlation values (0.85-0.15) except in LHAZ(-0.18). The stations GRHI and NPJG in the outer Himalayas show positive correlation values in all the three components(north,east,and the vertical).
The correlation coefficients between TWS and the north component of GNSS displacement show a roughly negative relationship. Interpolated correlation coefficients show which areas may have a greater impact on the TWS. However, such exceptions show anomalous results due to the local effects of groundwater irrigation, hydrology, and reservoir storage[19].
4.3. The strain rate estimation and its relation with seasonal TWS variation

Fig. 8. The interpolated correlation coefficient between TWS and the (a) north, (b) east, and (c) vertical displacement components, respectively.

Table 2 Site velocities(ITRF2014 and India fixed frame) with their seasonal components.
We calculated the baseline relative to the IISC station for linear strain measurements and magnified the amplitude of strain rate variation by multiplying by a factor of 10-9.Lower strain rates were observed in the co-monsoon compared to the pre- and postmonsoon, which is due to the predominance of non-tectonic or seasonal forces over the tectonic force. It can be seen from Figs. 4 and 5 that the strain rates decrease at CHLM, JIR2, DNSG, RMJT and JMSM stations when the hydrological load increases during the monsoon period.At the same time,the strain rates decrease sharply at BRN2, HYDE, and NPGJ. In HETA, KUGE, LCK3, LHAZ, NAST and SYBC, the strain rate decreases when TWS loading increases. The strain rate increases in post-monsoon but is low compared to that of the pre-monsoon since the effect of seasonal hydrological loading persists in post-monsoon to some extent.
Seasonal geodetic displacements show the lithospheric response to hydrological loading. When seasonal TWS loading increases during the summer monsoon,it induces extension or elastic deformation.In contrast,the compression or elastic rebound occurs when the seasonal loading decreases in the winter season (Fig. 9).
Seasonal hydrological loading also affects the seismicity. It can be seen from Fig. 6 that most of the earthquakes occurred in the central part of Nepal Himalayas.And almost 47.90%of earthquakes occurred in the pre-monsoon,17.56%in post-monsoon,and at least 15.97% during the co-monsoon. Fig. 7 shows that the incidence of earthquakes increases in pre-monsoon when TWS loading is low.During post-monsoon, the seismicity shows an inverse relationship with TWS since the impact continues to hover in postmonsoon. Whereas in co-monsoon, the occurrence of earthquakes is limited due to the effect of TWS loading. There are only four years with high seismicity in the pre-monsoon during 2003-2020,and the rest of years have high seismicity when TWS is less variable.Thus,the seismicity is inverse to the seasonal TWS/hydrological load variation.
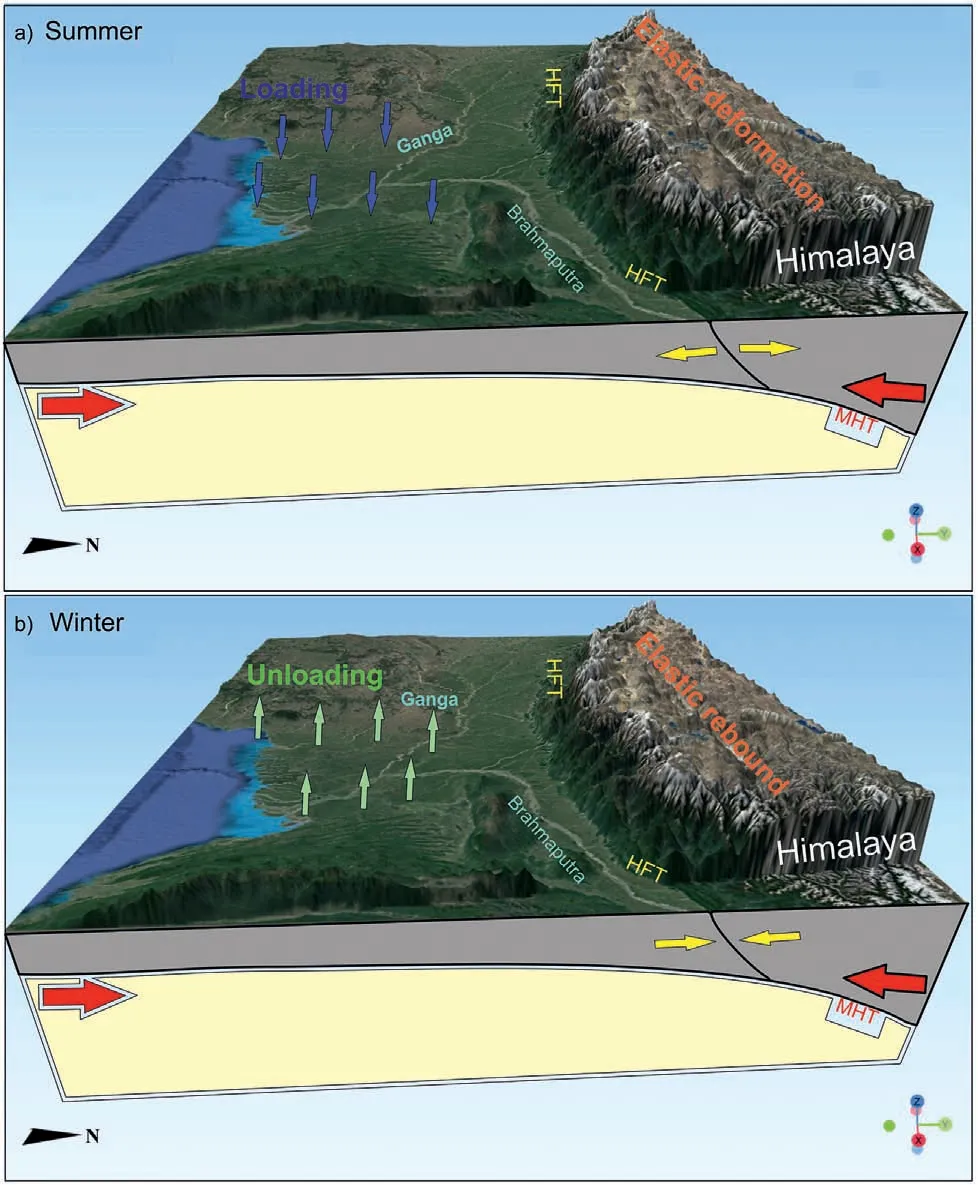
Fig. 9. The lithospheric response to seasonal loading variations. The red arrow indicates tectonic movement,and the yellow arrow denotes non-tectonic movement due to hydrological change.
5. Conclusion
The integration of GRACE and GNSS data (acquired from 21 GNSS stations) is used to study the impact of hydrological loading on the crustal deformation during 2017-2020. The TWS variation at the Ganga-Brahmaputra river is highest in co-monsoon compared to the pre- and post-monsoon. The horizontal displacement occurs in the direction of hydrological loading.In the case of vertical movement, it shows subsidence, and the reverse phenomenon occurs during unloading. The correlation coefficient between TWS and geodetic displacement infers a dominantly negative and positive relationship in vertical and east components,respectively. Seasonal displacements are estimated from strains at IISC stations,showing higher rates in pre-and post-monsoon when TWS variation is low. Similarly, seismicity is high in the pre- and post-monsoon. Therefore, we can infer that the strain rate and seismicity decrease as the seasonal hydrologic loading increases.
Conflicts of interest
The authors declare that there is no conflicts of interest.
Acknowledgments
We want to express our sincere gratitude to the Chairman of ISRO and the Director of IIRS for providing us facilities and motivation to complete this work.We are very thankful to Dr.Robert W.King (MIT) for providing GAMIT/GLOBK 10.70 software for processing the GPS data. We also express our gratitude to the University of Texas, Center for Space Research, IGS, and UNAVCO for providing GRACE and GNSS data products. We are thankful to Mr.Charan Chaganti for helping pre-process GNSS data and all those who have helped in data acquiring and processing directly or indirectly. The authors are also grateful to the Editor-in-Chief and anonymous reviewers whose suggestions and comments have supported the elaboration of this research.
杂志排行
Geodesy and Geodynamics的其它文章
- Three-dimensional coseismic deformation of the 2016 MW7.8 Kaikuora, New Zealand earthquake obtained by InSAR and offset measurements
- Dependence of epoch-wise two-way nested ANOVA estimates of variances of unmodeled effects present in relative GPS positioning on satellite elevation cutoff angle and PDOP mask
- Interseismic deformation rate of the Haiyuan fault system based on the modified SBAS method
- Delineation of sensitive coastal zone of northern Ramanathapuram coast, Tamilnadu, India, using a GIS approach
- The Doppler effect induced by earthquakes: A case study of the Wenchuan MS8.0 earthquake
- Three-dimensional gravity inversion based on optimization processing from edge detection
