基于ATAK的MSWEP数据空间降尺度及对降水融合的影响研究

云兆得，胡庆芳，2，王银堂，2，李伶杰，2，王磊之，陈建东

(1.南京水利科学研究院 水文水资源与水利工程科学国家重点实验室，江苏 南京 210029；2.长江保护与绿色发展研究院，江苏 南京 210098)

1 引言

随着卫星遥感、大气数值模式、陆面模型等技术的发展，国内外先后研制了一系列全球或准全球性的气候、水文、环境和生态要素的栅格数据集，为获取降水、气温、土壤含水量、陆地储水量、植被指数等变量的大范围空间分布信息提供了新途径。这些数据集的性能尺度持续改善，但在不少情况下其空间分辨率仍难以满足流域或区域尺度上的科学研究和实际工作需求。因此，国际上广泛开展了全球性空间数据的降尺度研究。

降水是基本的气象水文和生态环境要素之一，空间变异性复杂[1]。降水的空间降尺度方法包括动力降尺度[2]和统计降尺度[3]两类。其中，动力降尺度主要面向全球气候模式降水输出数据的空间尺度转换，需借助区域气候模式实现，具有物理机制较为明确的优点，但计算代价巨大，且计算结果仍不可避免受到区域气候模式局限性等因素的影响。而统计降尺度在物理机制上虽不及动力降尺度完善，但其算法更易于构造，灵活性更强，且计算代价远小于后者。因此，降水数据的空间统计降尺度的研究和应用十分广泛，国内外学者已发展了多元回归、广义可加模型、人工神经网络、多重分形等算法，这些算法大致可分为理想预报[4]、模型输出统计[5]、分位数映射[6]、随机天气发生器[7]等4类，还包括这4类方法的混合算法。

近年若干研究通过建立降水与高程、植被指数、大气湿度等地形地貌或气象因子之间的关系，实现热带降雨测量任务(Tropical Rainfall Measuring Mission，TRMM)等卫星遥感反演降水数据的空间降尺度[8-9]。这些研究的关键是建立降水与相关解释因子之间的多元回归关系，然而在一些情况下降水与地形地貌因子之间并不具备稳定和显著的统计回归关系，这在一定程度上限制了这些方法的使用。还有一些学者采用分位数映射方法直接对低分辨率的降水资料加以处理，但其主要作用是实现数据偏差校正，而非空间尺度转换，并且这种方法还要求具有一定的地表降水观测资料[10]。还有一些文献则采用反距离加权(Inverse Distance Weighted，IDW)[11]、双线性插值[12]等简单方法开展降水数据的空间降尺度，但这些方法通常会产生比较明显的平滑效应，同时也很少论述它们是否会破坏原始数据的空间结构特征。另外，有关IDW等简单方法与更复杂的降水空间降尺度方法所得结果的比较在文献中也不多见。

Kriging是建立在半方差函数基础上的一类空间估计方法，具有同时适用于点和区域尺度空间估计的优良特性。Kriging方法中的ATPK(Area to Point Kriging，ATPK)和ATAK(Area to Area Kriging，ATAK)提供了一种在没有地面降水观测数据的前提下，将低分辨率空间数据分别降尺度到点尺度和高分辨率的途径。ATAK可视为对ATPK的扩展，而ATPK可视为ATAK的一种特殊形式。已有文献从理论上证明了ATPK和ATAK不仅能够保持变量在不同空间尺度上的质量守恒[13]，而且能够保持空间相关结构特征，即半方差函数的守恒[14]。目前ATPK或ATAK已用于地区人口密度、土壤有机成分和房价空间插值等方面[15]。如Yoo等[16]最早将ATPK应用于人口普查区域数据降尺度，实现了人口密度在格网上的细化，其结果显示区域人口密度空间分布格网不仅保证了人口普查区域数据的质量守恒，而且具有较强连续性；Wang等[17]耦合ATPK和回归模型对MODIS波段观测数据进行空间降尺度，并验证了该方法准确地保留原始数据粗波段的光谱特性的能力；Hu等[18]根据粗糙和精细的两套气溶胶光学深度数据基于ATAK对缺失数据进行插值，结果显示ATAK能够较好地保留原始数据信息；Jin等[19]耦合地理加权回归和ATAK对土壤水分进行降尺度，证实了该方法具有局部空间异质性的刻画能力；Naeimehossadat等[20]分析了伊朗2003—2010年胃癌发病率数据，使用耦合ATAK与泊松分布的ATAPK方法和BYM方法进行空间插值并利用373个调查县的标准化胃癌发病率对插值结果进行检验，结果表明二者插值结果基本一致，但前者的平滑度较低，能够有效识别胃癌高发地区，具备较强的局部变异特征描述能力，精度也要优于后者。

由于降水具有很强的空间异质性，且属于区域型水文要素，不仅仅是对于单点的描述，因此为得到更细的格网降水，本文采用ATAK开展一种具有重要影响的全球性降水数据—多源加权集合降水(Multi-Source Weighted-Ensemble Precipitation，MSWEP)的空间降尺度研究，并在此基础上采用能够定量描述降水与相关影响因素之间非平稳性空间关系的GWR方法，进一步研究降尺度后的MSWEP数据与地表雨量站网观测数据的融合。本文一方面将比较ATAK和IDW对MSWEP进行空间降尺度处理后生成的雨量场差异，另一方面将解析不同背景场对MSWEP和地表雨量站网降水融合结果的影响，从而深化对降水空间降尺度和多源降水融合的认识。

2 研究方法

2.1 空间降尺度方法本文采用IDW和ATAK，在不考虑地表雨量观测资料的前提下，将MSWEP降水数据由0.1°×0.1°的空间分辨率降尺度至0.02°×0.02°。对于IDW方法，在对MSWEP数据空间降尺度过程中，将MSWEP雨量视为相应网格中心位置的“点”雨量，然后选择若干最邻近位置的雨量，通过加权平均生成各空间位置的雨量，其权重为距离倒数的幂函数。IDW插值是一种简单的经验性方法，计算量小，但显然没有考虑到不同尺度上降水空间结构特征的转换关系。

以下主要介绍ATAK对MSWEP数据进行空间降尺度的基本原理和步骤。对MSWEP数据，采用ATAK降尺度后生成的某一0.02°×0.02°格网单元降水量是其最近邻的m个降尺度前的0.1°×0.1°格网单元降水量的加权平均：

(1)

权重系数λi通过求解以下Kriging方程组得到：

(2)

式中：C(pi，pj)为0.1°×0.1°空间尺度上的两个格网单元之间的降水空间协方差(i，j=1，…，n)；C(p0，pi)为降尺度后的0.02°×0.02°格网单元与降尺度前的0.1°×0.1°格网单元之间的降水空间协方差(i=1，…，n)；μ为拉格朗日乘子。

对于ATAK而言，任意两个区域之间的空间协方差采用如下公式计算：

(3)

式中：us和ut为两个格网单元内的离散点；ni和nj为相应离散点数量；ws和wt分别为离散点us和ut对应的权重，在本文中其取值均为1；C(us，ut)为点尺度上的降水空间协方差函数。

由此可见，采用ATAK对MSWEP进行空间降尺度的关键是获取点尺度上的降水空间协方差函数或空间变异函数。但在缺乏站网雨量观测资料或者站网雨量观测资料稀疏的情况下，无法直接计算C(us，ut)。为解决这一问题，Goovaerts提出基于区域尺度的数据，通过图1所示流程图中的迭代过程获取点尺度的空间变异函数[14]，具体步骤如下：

图1 ATAK方法计算过程中点尺度变异函数拟合流程图

(1)根据降尺度前的格网单元降水量，计算0.1°×0.1°以及各种更大空间区域尺度上的经验空间变异函数；

(2)选择某种变异函数模型，对区域尺度的降水经验空间变异函数进行拟合；

(3)解设某一个点尺度上的理论空间变异函数，对其进行规则化处理(即求取区域尺度上的卷积)，得到各种区域尺度上的空间变异函数；

(4)反复调整步骤(3)中的点尺度的理论变异函数的参数，直至步骤(3)和步骤(2)得到的区域尺度的降水空间变异函数足够接近时，则说明步骤(3)假设的点尺度的降水空间变异函数模型可真实反映降水空间变异结构，进而通过式(2)—(3)得到降尺度后格网单元降水量估计结果。

由以上步骤可知，ATAK保证了点尺度上和区域尺度上的降水空间变异函数的“一致性”，这是该方法的突出优点。同时，Kyriakidi还从理论上证明了ATAK可保持不同空间尺度上的质量守恒[13]。

2.2 降水融合方法为阐明采用不同降尺度方法得到的MSWEP数据与地面站网雨量数据融合的效果，分别将原始的MSWEP数据、IDW方法插值处理的MSWEP数据和与ATAK降尺度后得到的MSWEP数据作为背景场，进一步采用GWR方法，通过站网降水资料对背景场加以修正，最后得到MSWEP和站网雨量的融合数据。

在具有实测数据的空间位置，以站点实测降水Po，i作为降水“真值”，以原始的或经过空间降尺度处理的MSWEP栅格数据Ps，i为背景值，则该位置降水误差为：

ei=Po，i-Ps，i

(4)

对于研究区域内没有站网观测数据的位置j，通过各邻近位置已知的降水误差估计，即：

(5)

最后将降水误差估计值叠加至背景场，即可得到融合后的降水估计值：

(6)

式中：Pj为位置j的降水融合结果；f为误差估计函数。

本文采用GWR方法处理式(6)中的误差估计函数f。GWR将回归模型参数表示为空间位置的函数，从而可以描述降水与相关影响变量之间的空间非平稳关系。在式(6)的基础上，GWR实现MSWEP与站点降水融合的主要原理如式(7)所示，其具体过程见文献[21]。

(7)

式中：(ui，vi)为待估点位置j的邻近观测点i的空间位置；βk(ui，vi)是观测点i的第k个回归参数(k=1，2，…，p)，随空间位置变化而变化；εi为残差，假设服从独立正态分布；xik为降水的第k个影响变量。

2.3 降水精度统计指标为解析MSWEP数据在空间统计降尺度以及融合前后的统计精度，本文以站点实测雨量资料为基准，采用平均误差(Mean Error，ME)、平均绝对误差(Mean Absolute Error，MAE)、相对偏差(Relatvie Bias，RBIAS)、相对绝对值偏差(Relatvie Absoulute Bias，RABIAS)、相关系数(Correlation Coefficient，CC)、纳什效率系数(Nash-Sutcliff Efficiency，NSE)6项指标评价降水估计精度。各指标计算公式如下：

(8)

(9)

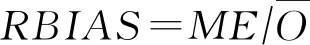
(10)

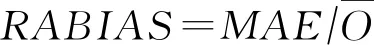
(11)

(12)

(13)

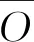
3 研究区域和数据

3.1 研究区域汉江是长江中游左岸最大支流，干流全长约1570 km，发源于秦岭南麓，流经陕西、湖北两省，最后在武汉市汇入长江。流域集水面积约15.9万km2，地理位置介于106°15′E—114°20′E和30°10′N—34°20′N之间(图1)。汉江流域多年平均降水量约900 mm，降水年内分布不均，汛期(5—10月)强降水多发。流域地形以山丘区为主，北侧为秦岭，南侧为大巴山和米仓山，中下游地区为江汉平原。汉江流域是南水北调中线调水区，在全国水资源配置中具有重要战略地位。

图2 汉江流域地理位置和雨量站点分布

3.2 数据资料

(1)MSWEP数据。MSWEP是由Beck等[22]研制的一套集成卫星遥感、大气再分析信息的全球性降水数据集，在某些区域还融合了一定的雨量站网观测信息。数据空间分辨率为0.1°×0.1°，时间分辨率3 h，时间跨度自1979年1月起始至今。MSWEP自发布以来就受到广泛关注。彭振华等[23]对比了包括MSWEP在内的5种使用频率较高的全球性降水数据集在中国不同气候区的精度，指出MSWEP的各项精度指标显著优于其它全球性降水数据集；但MSWEP对于降水细节的刻画仍有较大不足[24]，其空间分辨率和精度也有待提升。本文根据汉江流域空间范围，提取了2011—2014年相应格网的MSWEP降水数据，通过相应时次的3 h雨量累加得到逐月降水量。

(2)站点降水资料。汉江流域具有长系列地表雨量观测资料。根据水利部刊印的水文年鉴第6卷第14册，获取了2011—2014年汉江流域515个站点的逐月降水观测资料。根据图1，汉江流域中上游雨量站点较为密集，但下游局部地区较为稀疏。在降水融合计算过程中，根据515个站点的地理位置信息，采用K均值聚类将515个站点分成250个组，并分别从中挑选1个站点构成率定站点集合，用于率定GWR模型，使率定站点在空间上尽可能均匀分布，剩余的265个站点用于验证模型。

4 结果分析与讨论

4.1 降水空间降尺度结果采用ATAK和IDW方法，在不考虑地表雨量观测资料的前提下，将汉江流域2011—2014年MSWEP月降水数据由0.1°×0.1°的空间分辨率降尺度至0.02°×0.02°，生成了两套降水栅格数据，分别记作MSWEPATAK和MSWEPIDW。此外，本文将0.1°×0.1°分辨率的MSWEP原始数据记作MSWEPOrigin，以便于表述。

图3分别为2011—2014年汉江流域515个雨量站点实测月降水量与相应空间位置的MSWEPOrigin、MSWEPATAK、MSWEPIDW降水量的散点密度图。由图3(a)可知，在汉江流域MSWEPOrigin降水数据总体上低估了站网月降水量，ME和MAE分别为1.7 mm和19.6 mm，RBIAS和RABIAS分别为2.4%和27.8%，但CC和NSE均在0.80以上，证明MSWEPOrigin和站点雨量之间具有良好相关性，R2达到 0.81，表明前者对后者具有较强的方差解释能力，由此可见月尺度MSWEPOrigin数据在汉江流域的精度良好。MSWEPATAK与站网实测数据的各项精度统计指标要略优于MSWEPOrigin和MSWEPIDW，但相差甚小。图4进一步给出了MSWEPATAK等3套数据在2011—2014年的逐月空间精度统计指标箱线图，说明3套数据的各项空间精度统计也十分接近。这说明，虽然ATAK在原理上较为复杂，但采用该方法对MSWEP进行空间统计降尺度的过程中，因未采用MSWEP原始数据以外的额外信息，因此所得结果与简单的IDW方法插值生成结果，甚至与MSWEP原始数据在统计意义上相差不大。

图3 2011—2014年汉江流域MSWEPOrigin、MSWEPATAK、MSWEPIDW与雨量站点月降水量散点密度图

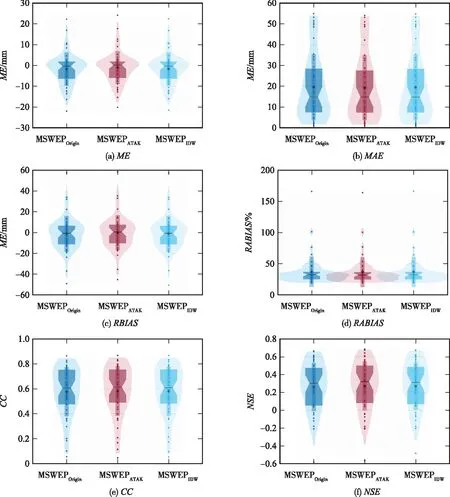
图4 2011—2014年汉江流域MSWEPOrigin、MSWEPATAK和MSWEPIDW月降水量的空间精度指标箱线图

然而，上述情况并不意味着MSWEPATAK与MSWEPIDW、MSWEPOrigin不存在差异。以2011年3月、2011年9月为例，图5、图6分别给出了这两个月份MSWEPATAK等3种数据对应的月降水量空间分布。显然，由于数据空间分辨率的原因，MSWEPOrigin对应的雨量场较为粗糙，其不连续性甚为突出。MSWEPATAK和MSWEPOrigin在降水空间分布格局方面具有一致性，但前者对降水场空间变化的描述显然较后者更具连续性。而MSWEPATAK与MSWEPIDW相比，前者对降水场局部特征的描述比较细致，而后者表现出明显的平滑效应。这说明，采用ATAK开展月降水量的空间降尺度过程中，由于不仅满足不同空间尺度上的质量守恒，而且保证了不同空间尺度上结构特征的一致性，因此对降水空间变异性的描述能力总体上要强于IDW，对雨量场局部变异特征的描述比较细致。此外，MSWEPATAK对应的2011年3月和9月雨量分布范围也略大于MSWEPOrigin和MSWEPIDW。

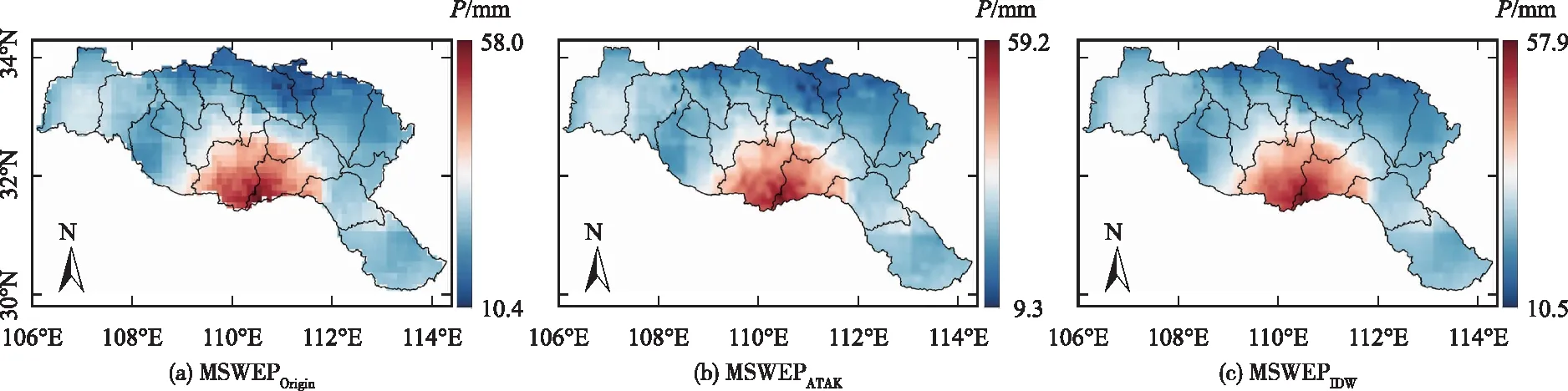
图5 2011年3月汉江流域MSWEPOrigin、MSWEPATAK、MSWEPIDW雨量空间分布

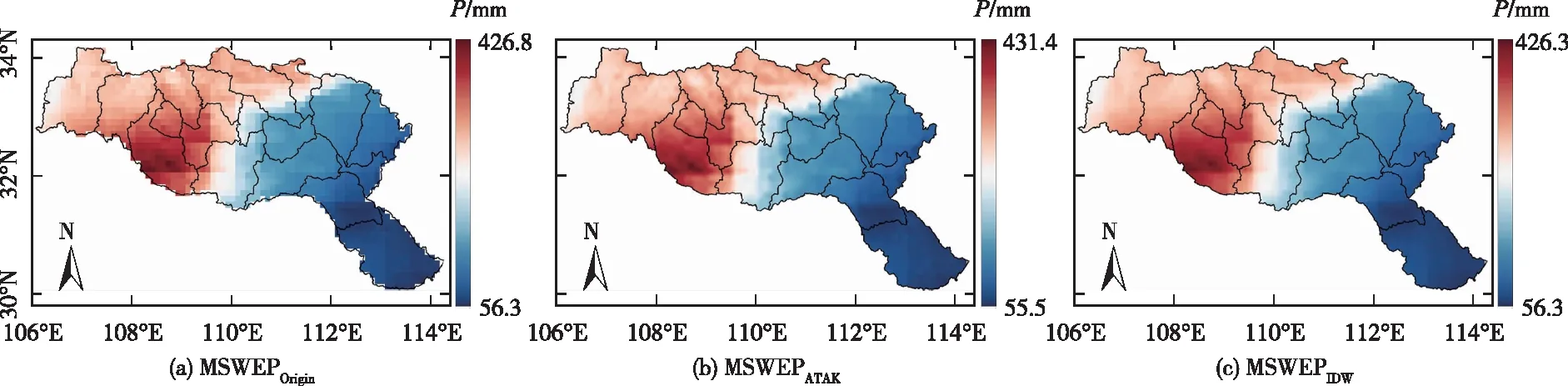
图6 2011年9月汉江流域MSWEPOrigin、MSWEPATAK、MSWEPIDW雨量空间分布

图7和图8进一步给出了2011年3月、2011年9月MSWEPATAK与MSWEPIDW、MSWEPOrigin的差值，为便于描述分别记作ΔP1和ΔP2。由于3月份为汉江流域枯水期，各网格月降水量较低，故从图7来看，2011年3月对应的ΔP1和ΔP2变化范围不大，但局部相对差异仍然明显，经分析两者雨量相对差异在5%以上的0.02°×0.02°网格单元有2632个。由图8可知，2011年9月MSWEPATAK与MSWEPIDW、MSWEPOrigin的总体上差异也不大，但在汉江流域中上游地区局部差异显著。在某些网格单元，MSWEPATAK明显高于MSWEPIDW，ΔP2最高达到42.6 mm；而在其它一些网格单元MSWEPATAK明显低于MSWEPIDW，ΔP2最低达-32.2mm。而MSWEPATAK与MSWEPOrigin的局部差异更明显，其范围介于-56.5～61.6 mm。进一步统计了2011—2014年所有月份MSWEPATAK与MSWEPIDW、MSWEPOrigin雨量差值，结果见图9。在0.02°×0.02°网格尺度上，ΔP1介于-56.5～61.6 mm，在汛期各月其变动范围较大、非汛期较小。ΔP2也有类似特点，其范围介于-44.8～47.7 mm。

图7 2011年3月 MSWEPATAK相对MSWEPOrigin、MSWEPIDW的雨量差异

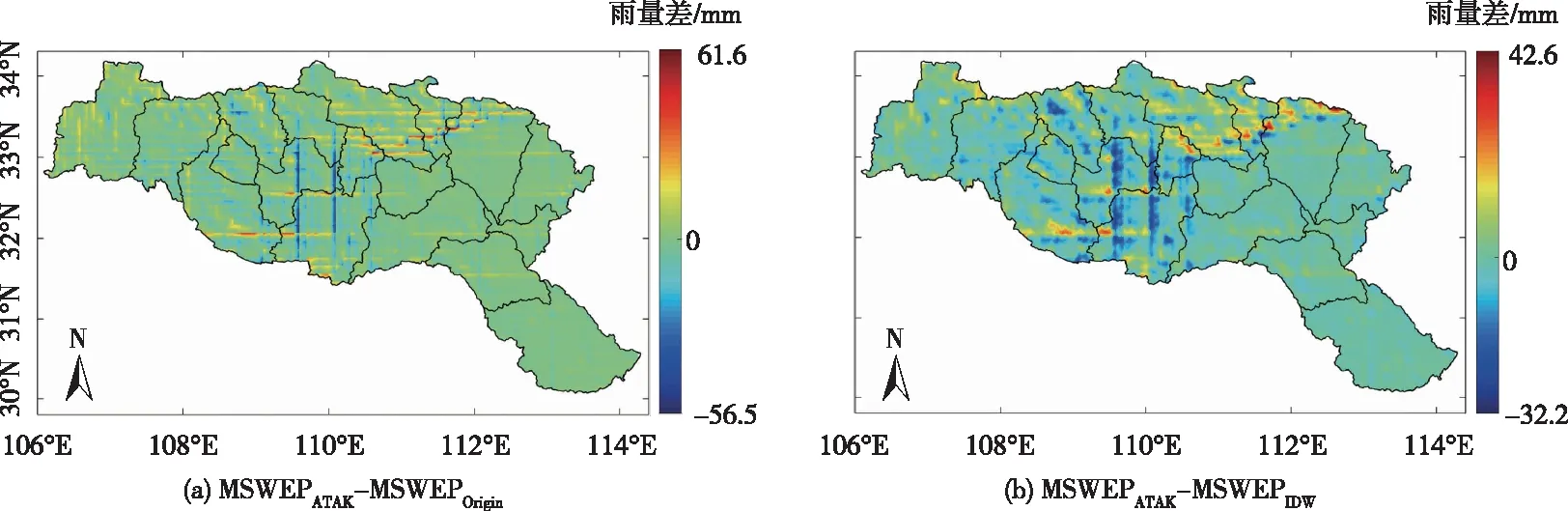
图8 2011年9月 MSWEPATAK相对MSWEPOrigin、MSWEPIDW的雨量差异

图9 2011—2014年各月MSWEPATAK与MSWEPOrigin、MSWEPIDW的雨量差异范围统计结果

图10给出了2011—2014年各月MSWEPATAK与MSWEPIDW、MSWEPOrigin雨量相对差异在不同区间的栅格单元数占汉江流域栅格单元总数的比例，为分别记作r1和r2。从中可知，大部分网格单元MSWEPATAK与MSWEPIDW相对差异小于5%，但相对差异超过5%以上的0.02°×0.02°网格单元数量最高可达25231个；对于MSWEPATAK和MSWEPOrigin也有类似规律。

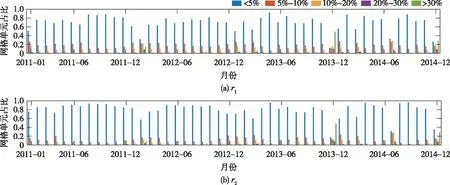
图10 2011—2014年各月MSWEPATAK与MSWEPOrigin、MSWEPIDW的雨量相对差异在不同区间的0.02°×0.02°网格单元占比

4.2 月降水融合结果为比较不同背景场对MSWEP和站点雨量资料融合效果的影响，分别以MSWEPATAK、MSWEPOrigin和MSWEPIDW作为背景场，采用GWR方法实现MSWEP数据与雨量站网观测数据的融合，在汉江流域生成了3套0.02°×0.02°空间分辨率的月降水栅格数据，分别记作MSWEPATAK-GWR、MSWEPOrigin-GWR和MSWEPIDW-GWR。图11—12为2011—2014年汉江流域站点实测月降水量与相应空间位置的MSWEPOrigin-GWR、MSWEPATAK-GWR、MSWEPIDW-GWR月降水量散点密度图。

由图11和图12可知，3种不同空间降尺度处理的MSWEP数据与地表雨量站网数据融合后，其精度显著改善，相关系数和效率系数进一步提高，定量误差削减明显。MSWEPATAK-GWR等3种降水融合数据与地表“真实值”已相当接近，同时相应的各项精度统计指标也较为接近。

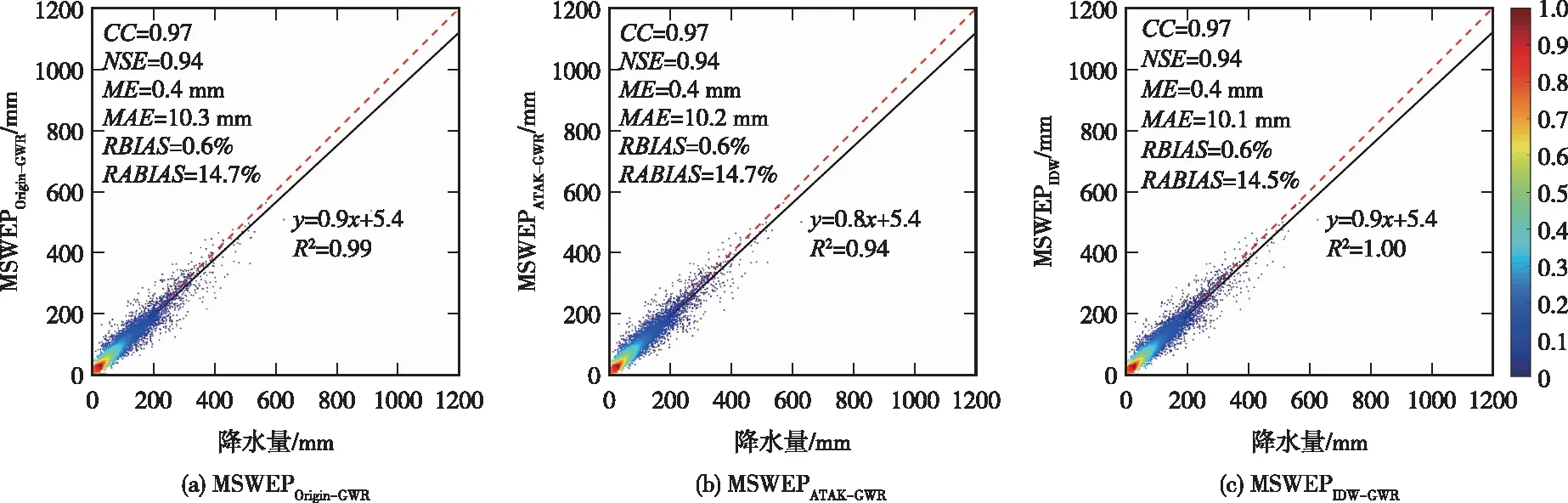
图11 率定站点处MSWEPOrigin-GWR、MSWEPATAK-GWR、MSWEPIDW-GWR与实测月降水量的散点密度图

图12 验证站点处MSWEPOrigin-GWR、MSWEPATAK-GWR、MSWEPIDW-GWR与实测月降水量的散点密度图

仍以2011年3月和9月为例，分析不同背景场与站网雨量数据融合后得到的降水场差异。由图13和图14可知，3种降水融合数据反映的月降水量空间分布格局总体一致，但MSWEPOrigin-GWR表现出明显的空间不连续性，这显然是受MSWEP数据未作空间降尺度处理的影响。MSWEPATAK-GWR和MSWEPIDW-GWR采用了空间降尺度后的MSWEP数据作为背景场，故月降水量的空间分布显然更加连续性。与MSWEPIDW-GWR相比，MSWEPATAK-GWR展现了更多细节性的空间变异特征。图15和图16分别给出了2011年3月和2011年9月MSWEPOrigin-GWR、MSWEPATAK-GWR与MSWEPIDW-GWR的差异。从中可知，在汉江流域多数格网单元，MSWEPATAK-GWR与MSWEPOrigin-GWR、MSWEPIDW-GWR无明显差异，但部分网格单元雨量仍存在显著差异。

图13 2011年3月MSWEPOrigin-GWR、MSWEPATAK-GWR、MSWEPIDW-GWR降水空间分布

图14 2011年9月MSWEPOrigin-GWR、MSWEPATAK-GWR、MSWEPIDW-GWR降水空间分布

图15 2011年3月MSWEPATAK-GWR相对MSWEPOrigin-GWR、MSWEPIDW-GWR的雨量差异

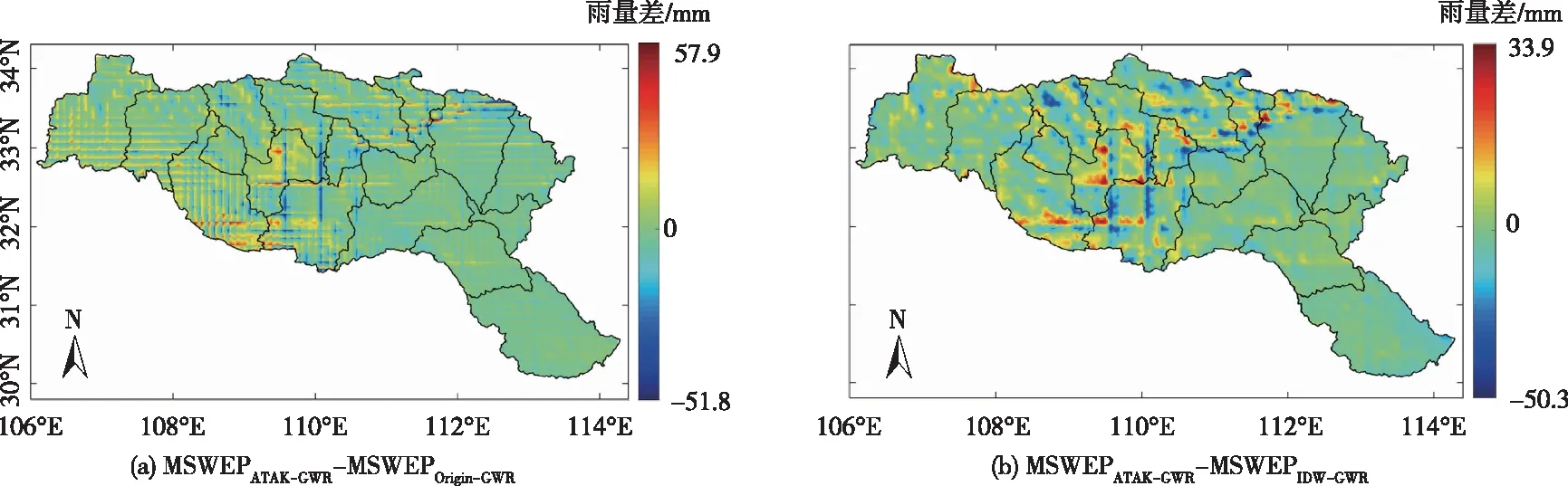
图16 2011年9月MSWEPATAK-GWR相对MSWEPOrigin-GWR、MSWEPIDW-GWR的降水空间分布差异

将MSWEPATAK-GWR与MSWEPOrigin-GWR、MSWEPIDW-GWR雨量差异分别记作ΔP1(GWR)和ΔP2(GWR)，图17给出了两者在2011—2014年各月的分布范围。尽管降水融合结果在很大程度上受雨量站网观测信息的影响[25]，在雨量站网较多的情况下，不同背景场对融合结果的影响会得到了弱化[21]，但是显然无法完全消除，甚至在局部得到了放大。如2011年7月等月份，在0.02°×0.02°网格尺度上，ΔP1(GWR)和ΔP2(GWR)接近甚至超过200 mm。图18进一步给出了2011—2014年各月MSWEPATAK-GWR与MSWEPOrigin-GWR、MSWEPIDW-GWR之间的相对差异(分别记作r1(GWR)和r2(GWR))超过不同阈值的在0.02°×0.02°网格单元占比。从中可知，r1(GWR)和r2(GWR)超过10%以上的格网数量仍有一定规模，这进一步说明了不同空间降尺度方法处理后MSWEP与站网数据融合的局部雨量差异是明显的。

图17 2011—2014年各月MSWEPATAK-GWR与MSWEPOrigin-GWR、MSWEPIDW-GWR之间雨量差异范围

图18 2011—2014年各月MSWEPATAK-GWR与MSWEPOrigin-GWR、MSWEPIDW-GWR的雨量相对差异在不同区间的0.02°×0.02°网格单元占比

5 结论

采用ATAK开展了全球性降水数据MSWEP在汉江流域的空间降尺度及MSWEP与地表站网降水信息的融合研究，解析了不同空间降尺度方法处理后的MSWEP数据与站网降水数据融合雨量的差异性，主要研究结论如下：

(1)ATAK是一种比较优良的空间降尺度方法，可在没有地表雨量站网观测数据等额外信息的情况下，实现MSWEP月降水数据的空间降尺度，并且在理论上可以保证不同空间尺度上降水的质量守恒，同时保证了不同空间尺度上降水空间变异函数的“一致性”，这对于提升全球性降水数据在无资料或少资料情况下的可利用性具有重要意义。

(2)MSWEP月降水数据采用ATAK进行空间降尺度前后，其统计精度指标变化不大，但较原始MSWEP数据具有更强的空间连续性，也在一定程度上克服了IDW插值方法进行简单空间降尺度处理的平滑效应，提高了对雨量场局部变化特征的描述能力。

(3)在地表雨量站网密度较高的情况下，MSWEP与站网降水融合结果在很大程度上受实测资料的影响，以原始MSWEP数据和ATAK、IDW降尺度处理后的MSWEP数据作为背景场与地表雨量数据融合得到的3套降水数据在精度统计指标方面十分相似，但背景场的差异对降水融合结果的局部影响不能完全消除，甚至可能会放大。

以上研究结论说明在对降水空间分布进行精细化的估计时，加强对全球性降水数据的空间降尺度方法的比较并选择适当方法是必要的，这为全球性降水数据的空间降尺度及其与地表雨量站网资料的融合提供了重要参考。但需要指出的是，本文仅开展了一种稠密雨量站网分布情况下MSWEP与站网降水的研究。今后应进一步在不同地表雨量站网密度及空间构形情况下融合MSWEP等全球性降水数据与站网降水数据，以深化对降水空间降尺度及多源降水融合效果的认识与应用。