DARMA模型在中国日降水量随机模拟中的适用性研究

曾文颖，宋松柏，康 艳，马 瑞，高 轩

(1.西北农林科技大学 水利与建筑工程学院，陕西 杨凌 712100；2.西北农林科技大学 旱区农业水土工程教育部重点实验室，陕西 杨凌 712100)

1 研究背景

降水作为水循环过程的主要驱动因素，受地理位置、大气环流、天气系统条件等因素的综合影响，呈现出复杂多变的特点。掌握降水事件的发生和降水量的分布规律，提高降水量模拟和预报精度，可为应对气候变化提供依据。我国降水资料观测长度较短，部分地区存在缺测等问题，导致无法为水和能量循环及气候变化等研究提供完备的数据支撑。因此，采用随机生成的方法，模拟样本降水数据的统计特征，生成的降水数据可以作为确定性水系统模型的输入，允许自然可变性和不确定性的传播，常用于水资源规划、水库管理、确定水力结构尺寸，以及估计干旱和洪水等极端水文事件，对于水资源管理具有重要的科学意义。

随机过程最早由Todorovic提出，随后被Yevjevich用于模拟短期降水，常用的参数模型包括自回归滑动平均模型(ARMA)及其改进模型，该模型假设序列正态分布，对于年降水和径流序列有较好模拟效果。对于非平稳的月序列，通过适当变换消除平均值和标准偏差中的周期性，使其近似正态分布后，也可以采用ARMA模型模拟。但ARMA模型自相关性随着滞后时间增加而显著降低，既不能保证观测序列持续性的再现，又不能保证不同月份序列之间的相关性结构。ARMA模型的正态性假设，使其不适用于模拟包括较长零值的日降水时间序列。

对于间歇性日降水事件，常采用马尔可夫链及其变换模型，这些模型考虑了不同降水状态之间的转移概率，可与非参数方法(如-近邻)相结合。一阶离散自回归模型DAR(1)也被称为一阶马尔可夫链，假设降水的概率仅取决于当前的干湿状态，而不会受到过去干湿状态的影响。Wilks采用一阶马尔可夫链模拟了美国纽约州25个站1951—1996年的日降水发生，表明DAR(1)能够保持研究区站点日降水量的相关性。Hannachi基于DAR(1)模型分析了北爱尔兰的逐日降水数据，发现冬季月份的自相关系数大于夏季月份的自相关系数。王福增通过一阶马尔科夫链和Gamma分布函数的联合应用，对黄淮海地区7个代表站连续42年实测降水资料进行随机模拟。研究结果表明DAR(1)结构简单，不需要大量的计算。然而，Semenov等发现DAR(1)模型无法模拟强旱日持续性情景，缺乏长持续性，且马尔可夫链的顺序可能受到季节变化和位置的影响。

选用高阶马尔可夫链可克服DAR(1)模型缺乏长持续性的问题，但必须使用更多参数，增加了模型不确定性和计算的复杂性。Jacobs提出了离散自回归移动平均模型(Discrete Auto Regressive and Moving Average，DARMA)的概念，旨在模拟具有指定边际分布和相关结构的离散随机变量的平稳序列。Buishand使用DARMA(1，1)模型成功模拟了热带和季风地区的日降水量。Muhammad系统研究了DARMA(1，1)模型模拟马来西亚日降水数据序列的适用性，模拟序列的干湿天数，并将统计数据保持在合理的精度范围内。Chung分析了非洲尼日尔河逐年径流时间序列，与DAR模型相比，DARMA模型更适合模拟具有较长高流量和低流量周期的径流量。此外，DARMA模型也被应用于干旱分析。DARMA模型对于长持续性离散事件概率分布具有较好模拟效果，可用于间歇性日降水量的研究。从文献研究结果来看，DARMA模型模拟精度优于传统的ARMA和DAR模型，体现了DARMA模型的潜在优势。但是，我国尚无关于DARMA模型在水文气象方面的研究报道。

基于此，本文采用DARMA模型对我国811个站点近60年来日降水量模拟进行研究。采用多日降水事件的概率分布和概率结构，建立DARMA(1，1)模型，模拟日降水事件的发生；根据不同游程降水事件分布函数，模拟湿日的降水量；以均值()、变差系数()、偏态系数()、最大一日降水量(1)和一阶自相关系数()为指标，评价模型模拟效果，并与DAR(1)模型进行对比，验证DARMA(1，1)模型在中国的适用性，以期为中国日降水量随机模拟提供新的模拟途径。

2 数据来源

本文采用中国地面气候资料日值数据集(V3.0)提供的全国气象站日降水数据，优选测站条件较好、建站时间早、缺测数据少、资料完整性好的811个气象站点，其空间分布如图1。统计各站点近60年的多年平均日降水量，发现日降水量由东南沿海向西北内陆递减；日平均降水量小于1 mm的站点占比16%，小于3 mm的站点占65%，最大日平均降水量为7.6 mm。

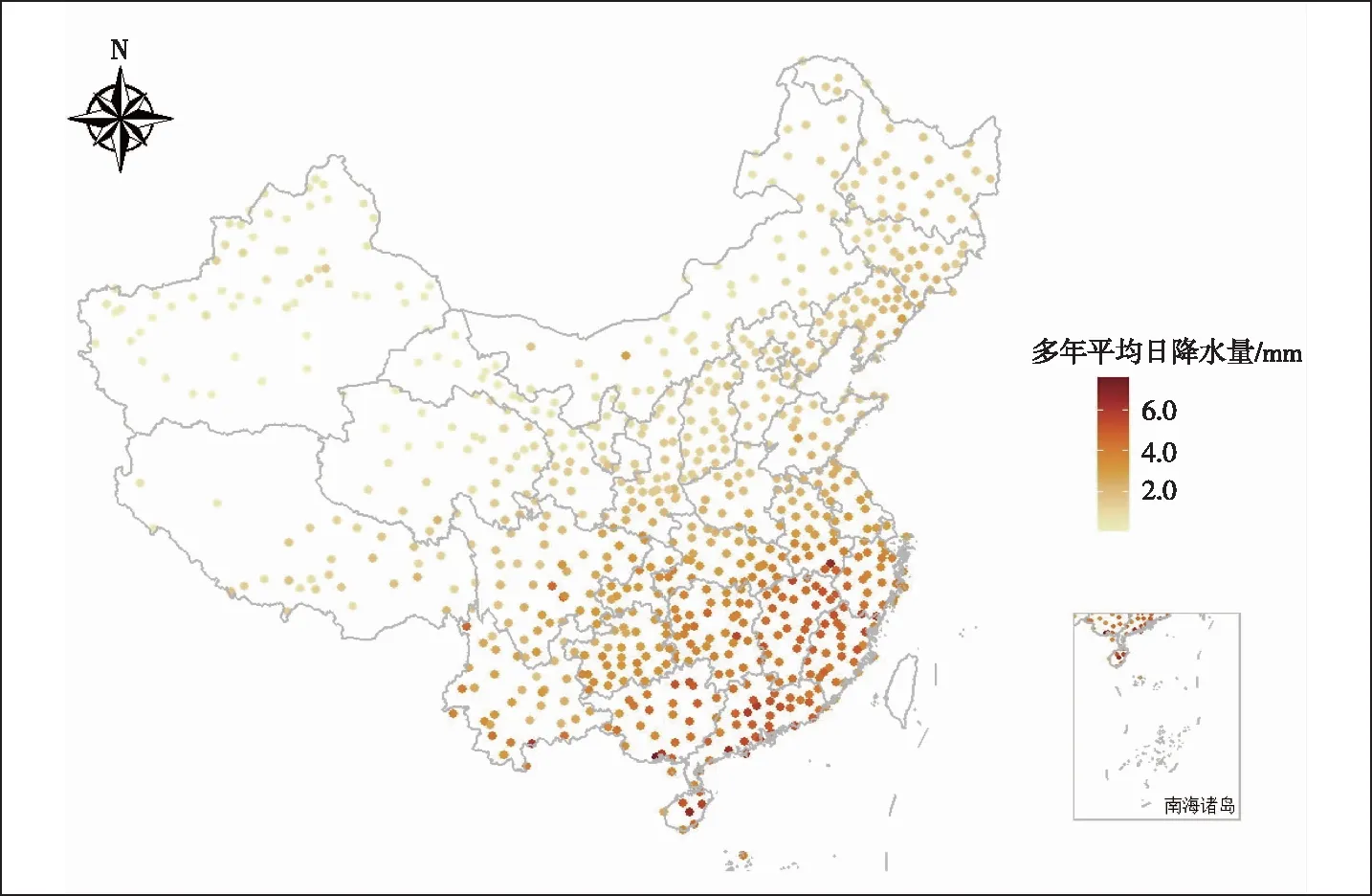
图1 研究区气象站点位置及多年平均日降水量分布图

3 研究方法

DAR(1)模型可表述为

=-1+(1-)

(1)

式中：为一个取值为0或1的独立随机变量，取0的概率为1-，取1的概率为

(=1)==1-P(=0)

(2)

为独立随机变量，取0的概率为，取1的概率为

(=)=，=0，1

(3)

为自回归分量，其表达式为

(4)

模拟过程从-1开始，模型的两个参数分别为(=1-)和，取值范围为(0，1)。由理论自相关函数(ACF)通过一阶自相关系数由式(5)估计，、π为样本序列平均干湿游程所占比例，由式(6)计算。

corr(，-1)=()=，≥1

(5)

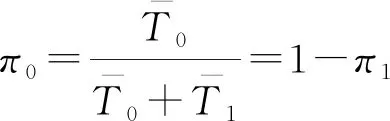
(6)

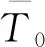
将DAR(1)模型的两个参数代入式(7)，计算一步转移概率，进而可得DAR(1)的一步概率转移矩阵式(8)

(，)=(+1=|=)

(7)

(8)

DARMA(1，1)模型的基本形式为

=+(1-)-1

(9)

式中：为取值为0或1的独立随机变量，取0的概率为1-，取1的概率为。

(=1)==1-P(=0)

(10)

将式(10)代入式(9)中可得

(11)

随机变量与具有相同的概率分布，且与相互独立，与构成一阶二元Markov链。DARMA(1，1)模型的三个参数分别为(=1-)、、，且取值范围为(0，1)。初值取/，采用牛顿迭代法，当式(12)取最小值时求得。

(12)

式中：为考虑滞后最大阶数；由DARMA(1，1)模型的一阶自相关系数确定。

corr(，-)=()=-1

(13)

且满足=(1-)(+-2)，解方程可得的取值为

(14)

将DARMA(1，1)模型的三个参数，代入式(15)计算一步转移概率，进而可得DARMA(1，1)的一步概率转移矩阵式(16)和(17)

(，)=(+1=，+1=|=，=)

(15)

(16)

(17)

DAR(1)和DARMA(1，1)模型检验主要包括ACF、干湿游程的理论值与样本值拟合效果评估。

(1)自相关系数ACF检验。样本经验自相关函数是根据干日和湿日的序列计算的，即0和1序列，计算公式为

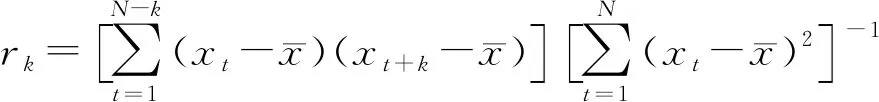
(18)

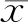
将通过式(18)计算的样本序列ACF值与式(5)和式(13)计算的理论ACF值进行对比分析检验。

(2)干湿游程检验。游程定义为同一类型事件的持续，它在开始和结束时由其他类型的事件界定。在模拟日降水序列时，DAR(1)的理论干湿游程长度数学表示为

(=)=(=0，=1，…，=1，+1=0|=0，=1)

(19)

(=)=(=1，=0，…，=0，+1=1|=0，=1)

(20)

采用DAR(1)模型的一步转移概率矩阵简化游程计算，可得理论干湿游程长度概率分布为

(=)=-1(1，1)[1-(1，1)]

(21)

(=)=-1(0，0)[1-(0，0)]

(22)

DARMA(1，1)的理论湿游程长度数学表示为

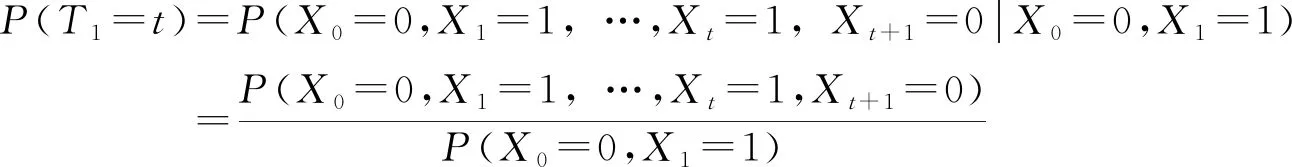
(23)

由与构成的一阶二元Markov链可得

(=0，=1)=(=0，=0)(+1=1，+1=0|=0)+(=0，=0)(+1=1，+1=1|=0)+(=0，=1)(+1=1，+1=0|=1)+(=0，=1)(+1=1，+1=1|=1)=[(0，0)+(1，0)][(0，0)+(0，1)]+[(0，1)+(1，1)][(1，0)+(1，1)]

(24)

(25)

化简式(24)和(25)可得DARMA(1，1)的理论湿游程公式为：

(26)

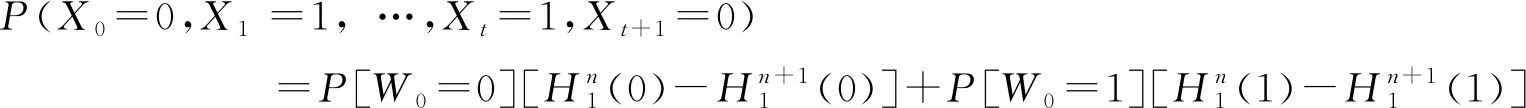
(27)

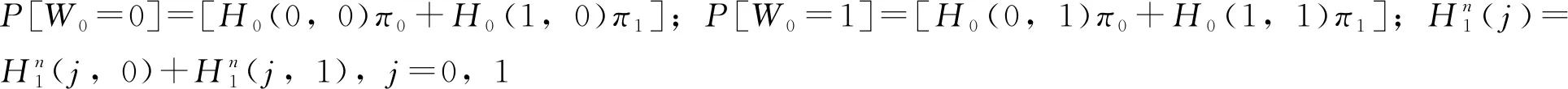
同理，可得DARMA(1，1)的理论干游程公式为

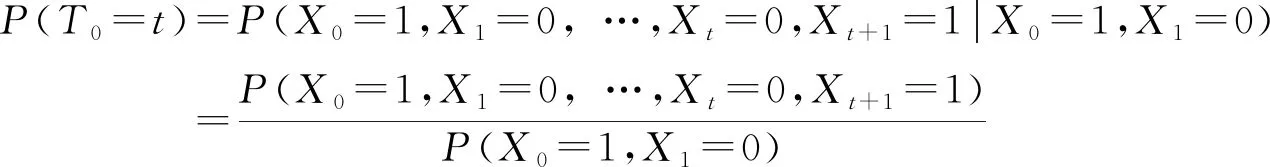
(28)

(29)

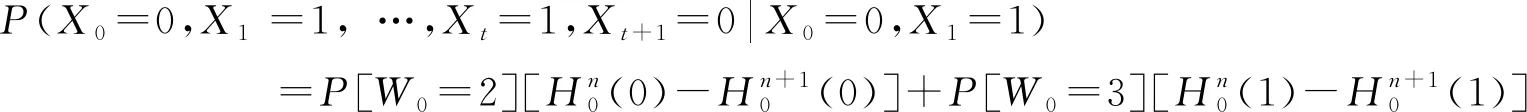
(30)

式中：[=2]=[(0，0)+(1，0)]；[=3]=[(0，1)+(1，1)]；

将通过Markov链分别计算的DAR(1)和DARMA(1，1)模型的理论干湿游程长度与样本序列干湿游程长度概率分布进行对比分析验证。

采用Gamma函数拟合日降水量分布，密度函数为

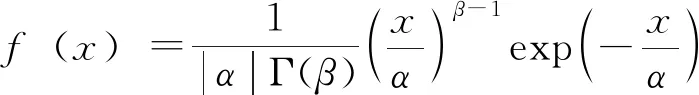
(31)

式中：为日降水量值；为形状参数(均值与标准差比值的平方)；为尺度参数(均值与形状参数的比值)。对密度函数进行积分可得日降水序列的分布函数。

DARMA(1，1)模型日降水量随机模拟的主要步骤为：(1)模型识别。使用ACF检验样本数据的自相关性，判断模型形式。若ACF逐渐衰减，则适合选用具有较长记忆的DARMA(1，1)模型；若ACF呈指数衰减，则适合采用DAR(1)模型。(2)模型参数估计。根据式(5)—(13)估计DARMA(1，1)和DAR(1)模型参数，并通过对比理论ACF与样本序列ACF进行模型初步检验。(3)模型选择。在确定模型结构时，湿游程和干游程长度模拟效果同样重要，可根据湿游程和干游程长度的样本和理论概率分布误差平方和最小选择模型。(4)模型模拟验证。首先生成随机变量，其中湿日和干日的离散概率分布分别为和；然后给定初值，生成序列，其中为-1和的概率分别为和1-；最后，根据概率和1-选择的移动平均分量和自回归分量部分。用蒙特卡罗方法随机生成100组长度为500+的干湿日序列，取序列长度为，以消除初值的影响。对模拟产生干湿日序列的ACF和干湿游程进行检验，并与实测序列进行对比。(5)日降水量生成。采用Gamma分布函数对样本序列中不同湿游程降水事件进行概率分布拟合，选用分布函数，按照产生的湿游程序列随机生成降水量，进行、、、1、的检验。

4 模拟结果分析

降水量的阈值(，mm)对于确定日降水事件的发生非常重要，干燥状态定义为一日降水量低于给定阈值。Muhammad指出，值高估无法真实反映降水过程，值低估则可能使日降水序列不均匀。参考顾学志关于中国日降水量分布的研究，选取中国日降水量阈值为0.1 mm，即日降水量大于0.1 mm视为湿日，小于0.1 mm视为干日，降水量大于0.1 mm持续天数视为一次降水事件的湿游程长，降水量小于0.1 mm持续天数视为一次干游程长。

本文选用测站条件较好、建站时间早、缺测数据少、资料完整性好的811个气象站点，计算所选811个测站序列、、、1和等统计值，并根据式(5)—(6)和式(12)—(14)，选择0.1 mm为降水发生的阈值，计算DAR(1)和DARMA(1，1)模型的参数和。本节以4个站点(51330、57278、57512和59849)为例说明模型建立及检验过程，其中51330站点日降水数据起止年限为1958—2017年，57278和57512站点为1959—2017年，59849站点为1956—2017年。经计算4站降水量统计值及模型参数见表1。

表1 4站日降水量统计值及模型参数

所选择的4个站点多年日平均降水量分别为0.7、2.3、3.1和6.6 mm，且地理位置横跨东西南北。通过日降水量统计值可以发现，不同站点和值无明显差异，沿海地区的最大一日降水量大于内陆地区，大部分地区不降水概率大于降水概率，而降水概率越大，日降水量序列自相关性越大。

由式(5)和式(13)分别确定DARMA(1，1)和DAR(1)模型的理论ACF，图解法比较样本和理论ACF如图2。总体而言，各站点的理论ACF衰减缓慢，最终在第8天附近趋于零，符合DARMA(1，1)模型的特征，证实DARMA(1，1)模型适用于中国气象站点的日降水序列模拟。DAR(1)模型的ACF呈指数衰减，以站点59849最为明显，在ACF滞时为2后出现明显衰减，导致与样本数据ACF出现较大误差。理论ACF检验结果显示，对于中国降水事件干湿序列的模拟，DARMA(1，1)更能保持较高滞后阶数的相关性。

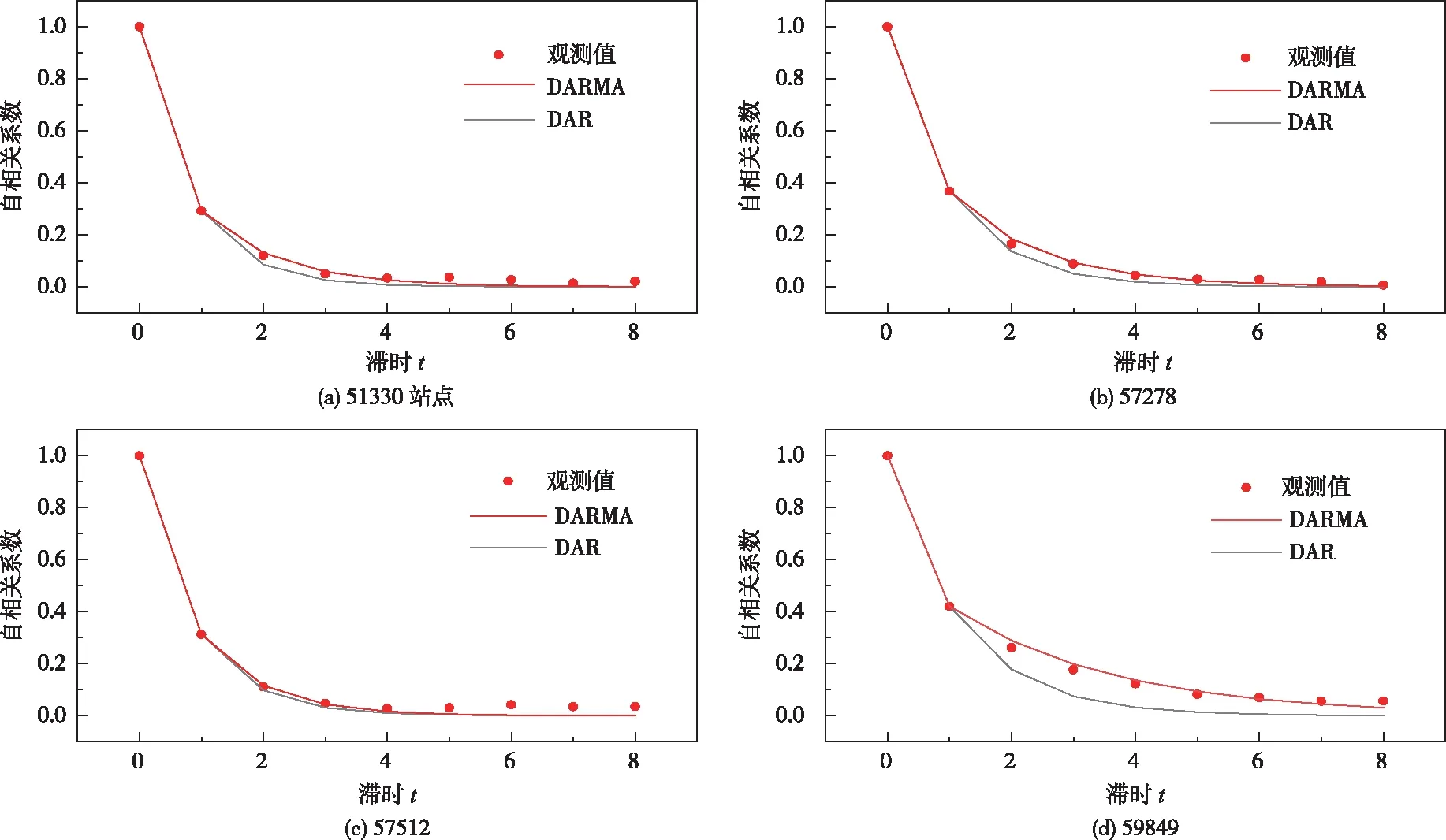
图2 理论和实测ACF对比图

在确定模型结构和阶数时，湿游程和干游程同样重要。因此，根据干湿游程样本和理论概率分布的平方和误差的最小值进行模型选择。通过式(19)—(30)计算DARMA(1，1)模型和DAR(1)模型的理论干湿游程概率分布，与样本序列进行对比，如图3所示。

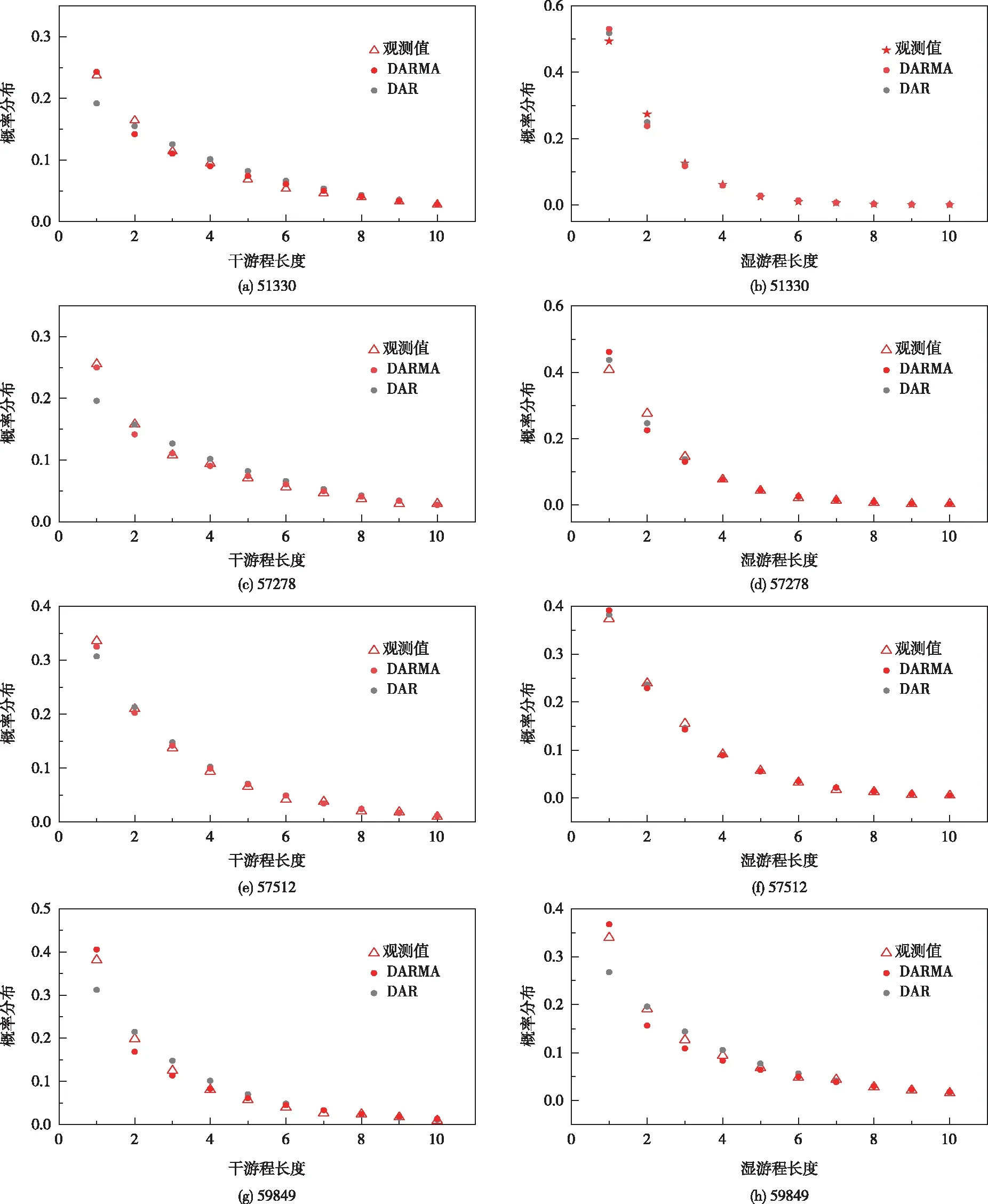
图3 理论和实测干、湿游程概率分布对比

从图3可知：(1)DARMA(1，1)模型能够在1到10个连续雨日和连续干日内生成概率误差最小，优于DAR(1)。对于51330站，DARMA(1，1)模型单个干日概率为0.2427，而实测数据计算概率为0.2368；对于51330站，DARMA(1，1)模型连续4个雨天的概率为0.0903，而实测数据计算概率为0.0943。(2)DAR(1)模型连续干日概率分布的模拟效果较差。对于57278站，DAR(1)模型单个干日概率为0.1959，而实测数据计算概率为0.2555；对于59849站，DAR(1)模型连续4个干日概率为0.1016，而实测数据计算概率为0.0810。理论干湿游程分布检验结果显示，DARMA(1，1)模拟所得误差平方和更小，较DAR(1)模型接近原序列干日概率。

用蒙特卡罗方法随机生成100组长度为500+的干湿日序列，取序列长度为，以消除初值的影响，将通过DARMA(1，1)和DAR(1)模型分别模拟产生的100组干湿游程概率分布，与原序列对比，选用结合箱形图与核密度图特点的分边小提琴图，显示统计数据及其整体分布和概率密度，更加直观地对比模拟结果，如图4所示，黄色点代表样本序列的干湿游程，红色小提琴和灰色小提琴分别代表DARMA(1，1)和DAR(1)的模拟结果，左侧4站点干游程长度概率分布和右侧4站点湿游程长度概率分布均显示了，模拟数据计算和样本数据计算具有良好的一致性。这一结果表明，模拟的日降水序列能够重现原始数据集的参数和特征。

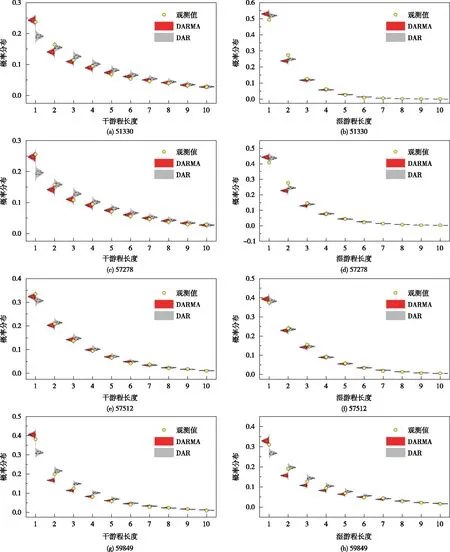
图4 模拟和实测干、湿游程概率分布对比图

表2总结模拟生成的100组降水0-1序列的平均ACF误差和干湿游程均方根误差的统计信息。其中，DARMA(1，1)模型的ACF误差和干湿游程误差和均在0.03以内，干、湿游程误差在0.02以内，DAR(1)模型的ACF误差和干湿游程误差和均在0.06以内，干、湿游程误差在0.03以内；DARMA(1，1)模型的干游程概率分布拟合更优，DAR(1)模型则拟合出具有较小误差的湿游程概率分布；随着站点年降水量的增加，多日降水事件出现概率增加，DARMA(1，1)在湿游程概率分布的拟合上也优于DAR(1)模型。整体而言，两种模型的模拟结果与原序列特征值较为接近，模型合理，而DARMA(1，1)对长持续性事件模拟具有更高的精度，验证了Muhammad和Chung的研究结果。

表2 DAR(1)和DARMA(1，1)模型的ACF和干、湿游程平方和误差分析

首先对原序列一日降水、连续两日、连续三日降水等不同持续天数的降水事件进行划分，为避免因较大游程出现次数少无法进行分布拟合的情况，取较大游程出现次数大于10为有效游程，记最大湿游程为，选用二参数Gamma分布对不同游程的降水事件进行分布拟合，分别得到不同持续天数降水量的分布函数。将全国811个站点模拟产生的0-1干湿序列进行游程划分，采用对应的分布函数对不同降水事件进行降水量的随机生成，当模拟湿游程大于样本序列最大湿游程时，采用最大湿游程对应分布函数来随机生成降水量。

绘制DARMA(1，1)模型拟合得到的各站点日降水量、、和误差如图5，颜色越深，说明模拟误差越大。由图5可以发现：(1)4幅图整体颜色较浅，大部分站点拟合效果好；(2)东南沿海误差小，西北内陆误差大。西北地区地处亚欧大陆腹地，主要受西风带气流的影响，来自海洋的水汽难以到达，形成干旱少雨的基本气候特征，复杂的地形分布使降水时空分布极不均匀，降水量大值主要集中在山脉地区，而山区降水又呈现出历时短、强度大的特点，这种降水特点导致降水量序列的自相关系数迅速衰减，而DARMA模型更适合于模拟ACF衰减缓慢的长持续性降水序列。因而西北内陆误差较东南沿海大，与降水量从东南沿海向西北内陆递减有较大关联；(3)新疆、西藏和内蒙古等部分少降水地区误差较为明显。分析结果显示，DARMA(1，1)模型能保持各站点日降水量的统计特征值及自相关性，适用于中国日降水量的随机模拟，且在东南沿海效果更好。

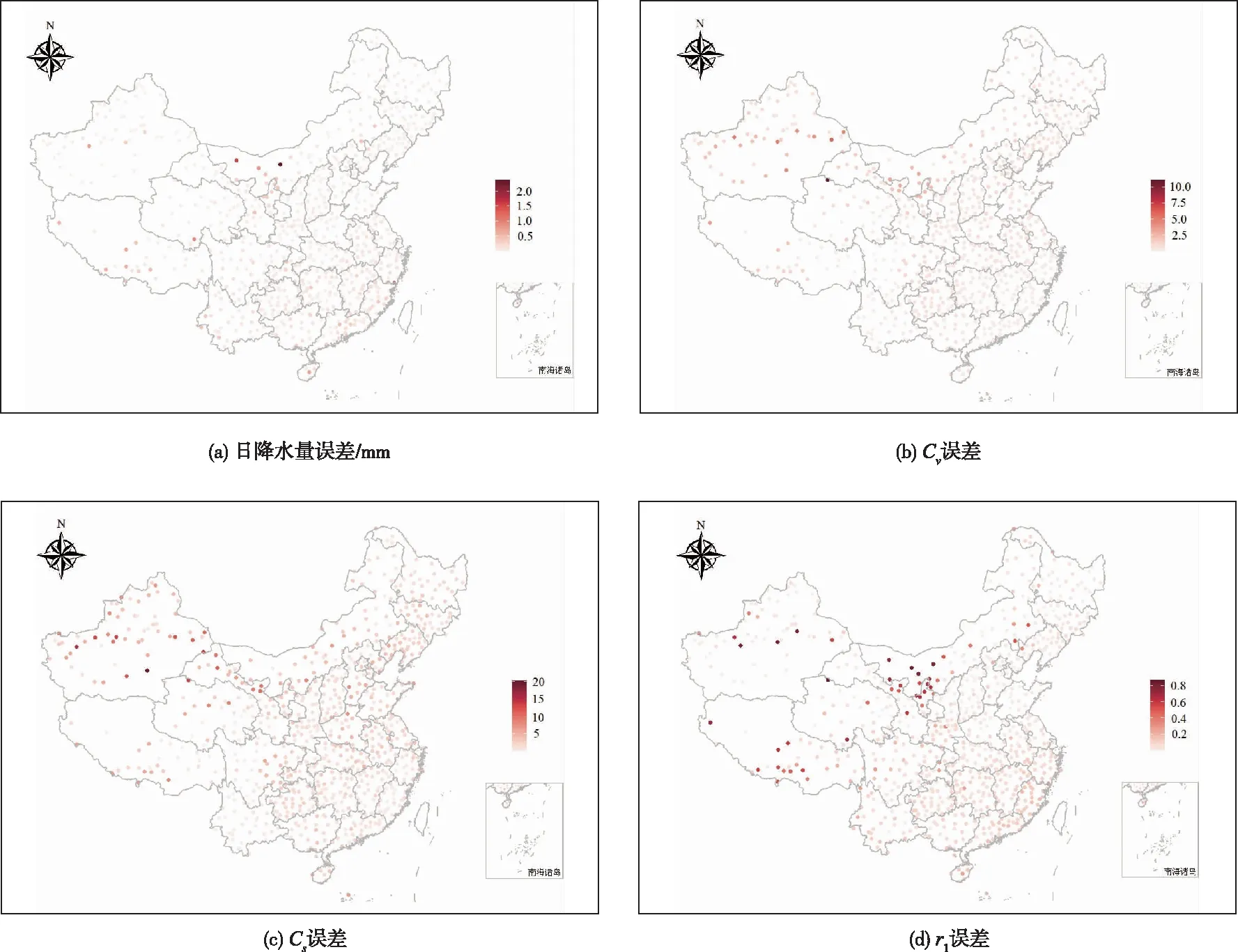
图5 DARMA模型拟合各站点日降水量均值、Cv、Cs、r1误差图

按多年平均日降水量大小对站点进行划分，讨论模型DARMA适用性。其中，0～1 mm有130个站点、1～2 mm有270个站点、2～3 mm有134个站点、3～4 mm有142个站点、4～5 mm有99个站点、大于5 mm的站点有36个。计算不同多年平均日降水量区间内，DARMA(1，1)和DAR(1)模型各100组模拟日降水量的、、、1和的平均误差，并统计拟合更优的站点占比情况，计算结果如表3所示。

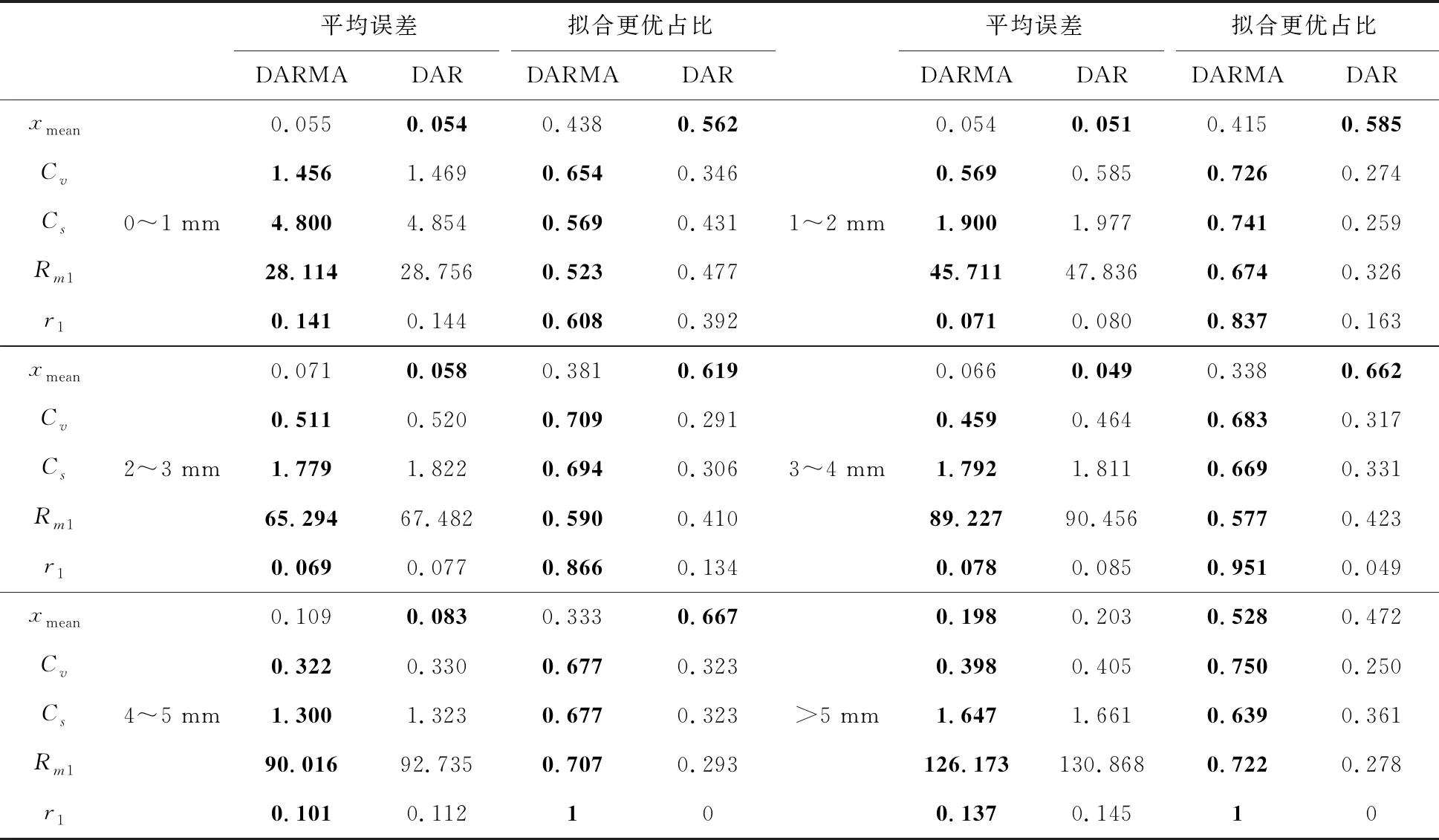
表3 不同降水区间日降水量模拟平均误差及拟合更优占比统计表

从表3可以发现：(1)降水量较小区域均值误差在0.05 mm以内，降水量较大区域误差为0.1 mm以内，在多年日平均降水量大于5 mm地区误差为0.2 mm以内，DARMA(1，1)模型的平均误差为0.099，DAR(1)为0.107，模拟效果较好；(2)由于序列中存在大量无降水日，使得原序列的和值较大，且最大一日降水量出现的不确定性高，在随机抽样的过程中产生一定误差；(3)DARMA(1，1)模型的、、1和平均误差小于DAR(1)模型，拟合更优站点占较多比重，更好的保持了实测日降水量的统计特征值，模拟的序列具有实用性；(4)在多年平均日降水量小于5 mm的地区，采用DAR(1)模型模拟所得日降水量均值的误差更小，随着降水量的增加，具有长持续性特点的DARMA(1，1)模型在日降水量均值的模拟上，逐渐优于DAR(1)模型，在多年平均日降水量大于5 mm的地区，DARMA(1，1)模拟的均值误差为0.198，小于DARA(1)的误差0.203，且有52.8%的站点都是DARMA(1，1)更优；(5)随着多年平均日降水量的增加，DARMA(1，1)模型的优势更加明显，均值更优站点占比从0.438增加到0.528，更优占比从0.654增加到0.75，从0.569增加到0.639，1从0.523增加到0.722，更优占比变化最为明显，从0.608增加到1。

选取的5个评价指标中，若同一模型有大于等于3个指标与原序列更为接近，则认为该模型为该站点的最优拟合模型，统计发现811个气象站点中，有518个站点为DARMA更优，占比64%，绘制最优拟合模型分布图如图6，黄色为DAR模型最优，绿色为DARMA模型最优。由图6可知，在云南、广东、广西和江浙一带DARMA最优占比在90%以上，而新疆、青海、兰州等地DAR模型占比较其他地区更高。

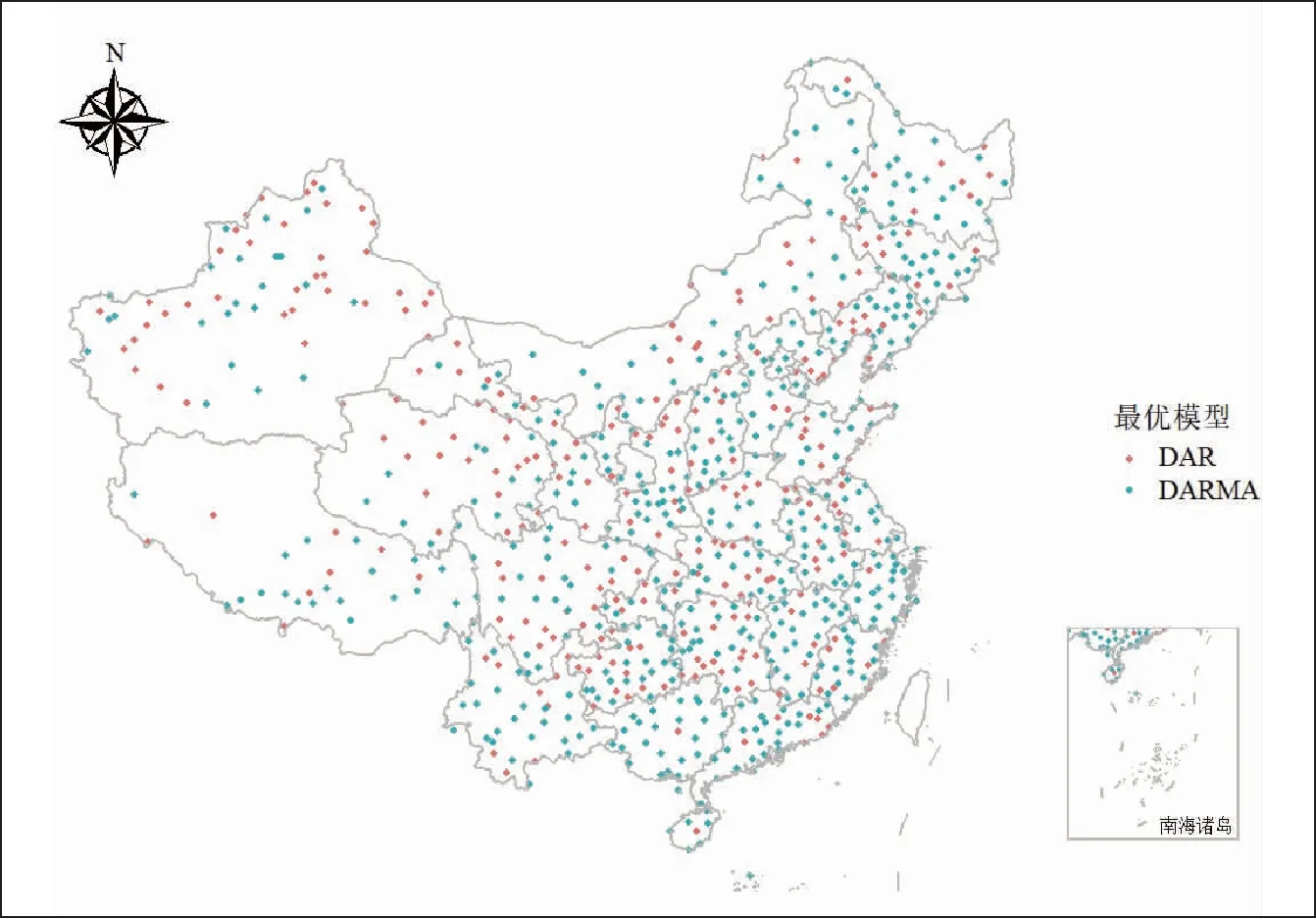
图6 全国各站点最优拟合模型分布图

以上分类讨论结果显示，除均值以外，采用DARMA(1，1)模型拟合的日降水量在保持实测序列各统计特征值方面，优于DAR(1)模型，与原序列更为接近。对于模拟产生日降水量的均值，DAR(1)模型在多年平均日降水量小于5 mm地区效果更好，而DARMA(1，1)模型在多年平均日降水量大于5 mm地区更具优势。在工程实践及水资源规划管理中，对降水量大、多日降水事件频发地区选用DARMA(1，1)模型；在对降水量较小地区进行随机模拟时，若、、1和为重要指标则选用DARMA(1，1)模型，若均值为重要指标则可选用DAR(1)模型。

5 结论

本文以测站条件较好、建站时间早、缺测数据少、资料完整性好的811个气象站点日降水量数据为研究对象，通过多日降水事件的概率分布和概率结构，建立DARMA(1，1)模型，模拟干湿游程分布，对理论和模拟ACF及干湿游程概率分布进行检验，验证了模型的合理性和普适性。通过Gamma函数生成不同游程降水事件的日降水量，以、、、1和为指标，评价模型模拟效果，并与DAR(1)模型进行对比，得到结论：DARMA(1，1)模型对干游程概率分布拟合效果好，对于湿游程分布的拟合效果随着多日降水事件出现概率增加而提升；采用DARMA(1，1)模型拟合的日降水量，、、1和等指标总体优于DAR(1)模型，在降水量大、多日降水事件频发地区均值也优于DAR(1)模型。

整体而言，DARMA(1，1)模型的模拟结果与原序列特征值较为接近，适用于中国大陆地区日降水量的随机模拟，且对长持续性事件的模拟具有更高的精度，是一种非常具有应用前景的日降水量模拟模型。在后续研究中，将考虑变化环境对模型参数的影响，引入时变参数、随机波动特性等对模型进行进一步探索，或开展高阶DARMA模型研究，以期在模拟过程中捕捉更多降水特征，提高模型精度。

(文中中国地图的审图号为：GS(2020)4632)