临床试验中纵向缺失数据不同处理策略统计性能的比较

赵淑珍，金东镇，李慧慧，赖梦园，黄若谷，毛广运，2

1.温州医科大学 公共卫生与管理学院 预防医学系，浙江 温州 325035；2.温州医科大学附属眼视光医院 国家眼部疾病临床医学研究中心，浙江 温州 325027

新药临床试验研究中，受试者由于各种原因而中途脱落的现象极为常见，由此导致的数据缺失问题不可避免地影响着研究结论的准确性和可靠性[1]。虽然缺失数据的处理一直是统计学的重要研究热点之一，但目前尚未达成针对缺失数据处理的共识。临床科研实践中对缺失数据的处理方式往往较为简单，甚至带有个人偏好[2]，其中尤以盲目删除缺失数据的相关记录和使用末次观测结果进行结转最为常见[3]。研究发现，简单地删除缺失记录不仅可能会导致统计学把握度（Power）的降低，增加假阴性结论的发生风险，还可能因破坏了随机性及降低样本的代表性，给试验结果带来不可忽视的偏倚效应[4]。此外，末次结转的前提条件是数据缺失的机制必须为完全随机缺失，事实上很少有研究能满足这一要求，并且由于该方法中的效应估计相对保守，甚至会较大程度影响到研究结论的准确性[5]。多年来，尽管各种缺失数据的处理方式不断涌现[6-8]，但由于均未同时充分考虑缺失模式、缺失机制及缺失比例的影响，尚无能够完美解决临床试验中数据缺失问题的方法被广泛认可。本研究旨在基于电脑模拟数据，深入分析评估不同处理策略在相关数据缺失模式、机制和比例下的性能，为科学合理地处理新药临床试验的缺失数据提供依据。

1 资料和方法

1.1 数据模拟方法 根据CHRIS等[9]提供的SAS代码生成完整双臂优效性临床试验模拟数据集，数据基本情况见表1，变量包括受试者编号、年龄、性别、访视时间和结局水平测量。其中性别及组别由伯努利分布随机生成，总样本量为500，其中安慰剂组262例，试验组238例，女220例，男280例；年龄和基线指标由正态分布随机生成，年龄分布为（48.6±15.2）岁，基线目标水平为（99.95±10.74）。访视时间分别为基线、给药后1、2、4、6、14 周。访视过程中对照组后续随访每次目标水平的测量由均数为100、标准差为10的正态分布随机数替代，而试验组访视过程中目标水平的测量由上一访视时间点的测量结果加上新的均数为10，标准差为2的正态分布随机数替代，完整数据集在各个时点表现见表2。将上述完整模拟数据集分别处理成完全随机缺失和随机缺失机制下的任意缺失模式和单调缺失模式。考虑到很少有临床试验的数据缺失比例会超过15%，故此分别设置了0%～10%、5%～10%和10%～15%三个等级数据缺失比例展开相关研究。

表1 模拟数据基本结构

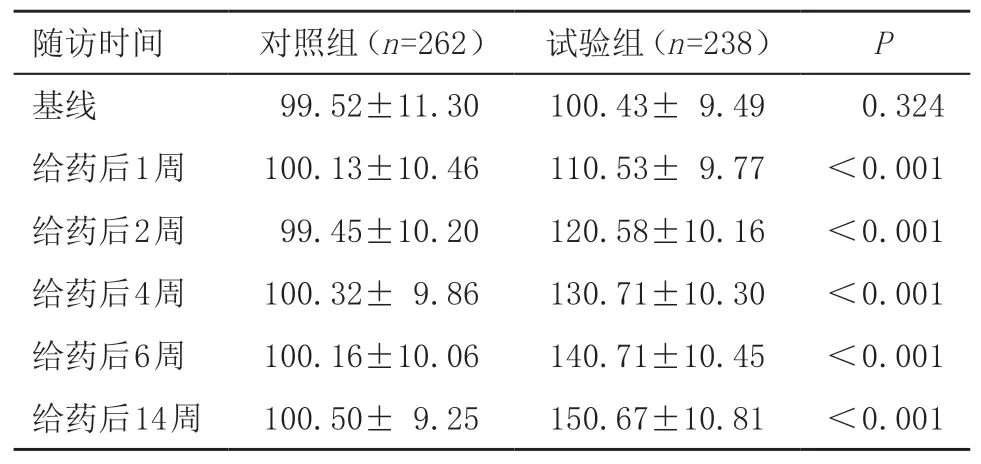
表2 完整模拟数据的基本信息

1.2 缺失值数据处理方式 目前临床试验中针对缺失数据常用方法有四类：基于完整数据集、基于填补、基于极大似然和基于非随机缺失机制。其中，由于基于完整数据的方法常将带有缺失数据的记录或变量直接删除，违背了意向性分析（intentionto-treat, ITT）原则，并降低检验效能，最终导致结论发生偏倚，因此不推荐其作为临床试验中处理缺失数据的主要方法[10]。

基于填补法是利用已观测到的数据填补未观测数据，主要为单一填补和多重填补。其中，单一填补方法中目前最为广泛使用的主要有基于末次观测结转、基线观测结转、最差观测结转，即分别用最后一次观测数据、基线观测数据以及随访过程中最差一次观测数据分别进行填补。虽然单一填补方式操作简单，但由于其低估了数据的变异，并且对数据缺失机制要求严格[11]，常被作为敏感性分析内容。同时，作为敏感性分析内容之一，最差个例分析也常被纳入考量，即对照组用最佳观测结转，试验组用最差观测结转[12]。作为单一填补的延伸，多重填补则给数据集中每一个缺失值做n次填补，而后对填补好的n个完整数据集分别进行统计分析，综合n次分析结果后得出最终结论[13]。多重填补中常用的方法包括回归模型、预测均值匹配、全条件定义法（fully conditional specification, FCS）等。回归填补指建立填补变量与协变的回归方程后，基于此方程从参数的后验预测分布模拟出新的方程用于缺失值的填补[14]。预测均值匹配通过线性回归填补模型为缺失值计算得填补值后，选取最接近填补值的K个已观测数据后从中随机挑选一个进行填补[15]。FCS则是利用单个数据的条件分布建立一系列回归模型逐一填补并迭代[16]。不同方法适用条件不同，如当数据缺失模式为单调缺失，缺失变量为连续型变量时，建议选择单调回归或单调预测均值匹配方法进行填补。而当数据缺失模式为任意缺失，缺失变量为连续型变量时，建议选择FCS回归或FCS预测均值匹配[17]。

基于极大似然的方法不需要对缺失数据进行填补，而是基于观测数据对模型总体参数进行估计。常用的基于极大似然的方法主要有重复测量的混合效应模型（mixed-effects model repeated measures, MMRM）[18]。由于在重复测量的数据中，重复测量因素的各水平之间往往存在一定的自相关性，因此其分析方法有别于一般统计分析。除选择合适的固定以及随机效应外，选择合适的方差-协方差矩阵结构对模型进行拟合也十分重要。常用的方差-协方差矩阵结构主要有非结构化协方差、复合对称协方差、托普利茨协方差、一阶自回归协方差等。对均衡完整资料的重复测量设计通常假定其方差-协方差矩阵结构是非结构化（即任意两时点间的相关不等或不全相等）或复合对称的（即任意两时点的相关是相等的）[19]。考虑到重复测量的时间点是从大量时间点中选取出的一个随机样本以及缺失数据可能带来的影响，采用不同的协方差矩阵结构进行敏感性分析也十分有必要。

此外，由于以上处理方法大多针对完全随机缺失或随机缺失机制，但在临床试验中，具体缺失机制难以确证，因此，实践中通常建议增加非随机缺失机制下的缺失数据处理方式作为敏感性分析[12]。由于模式混合模型（pattern-mixture models, PMM）[20]对缺失数据分布假设易于解释并具有临床意义，在实践运用较为普遍[11]。

基于以上分析策略，本研究分别采用包括不同协方差矩阵结构的MMRM模型（非结构化协方差、复合对称协方差、托普利茨协方差、一阶自回归协方差），单一填补（基于末次观测结转、基线观测结转、最差观测结转、最差个例分析）、多重填补（不同填补次数的预测均值匹配与回归）及PMM的协方差分析（analysis of covariance, ANCOVA）对构造的缺失数据进行处理，具体各缺失值处理方式见表3。以治疗14周较基线变化差值为主要疗效指标，对单组疗效以及组间疗效差异进行评估，并与完整数据集估计结果进行比较。

表3 缺失值处理分析方法

2 模拟试验结果

2.1 完全随机缺失机制-任意缺失模式 当缺失比例小于5%时，不同缺失数据处理方式对单组疗效以及组间疗效差异的估计结果均非常接近真实情况，各方式间未出现明显差异，见图1。随着缺失比例的升高，各种处理方式在同组内部各时点的疗效估计性能均出现了不同程度的下降。此外，单一填补及模式混合模型均会明显低估治疗组的疗效，而MMRM及多重填补的结果则较为稳定。值得注意的是，不同MMRM以及基于不同填补次数和填补方式的多重填补对结果均无明显影响。而在组间疗效差异估计中，除了MMRM以及多重填补表现出较高的稳定性外，其余方式均会受到不同缺失比例的影响。

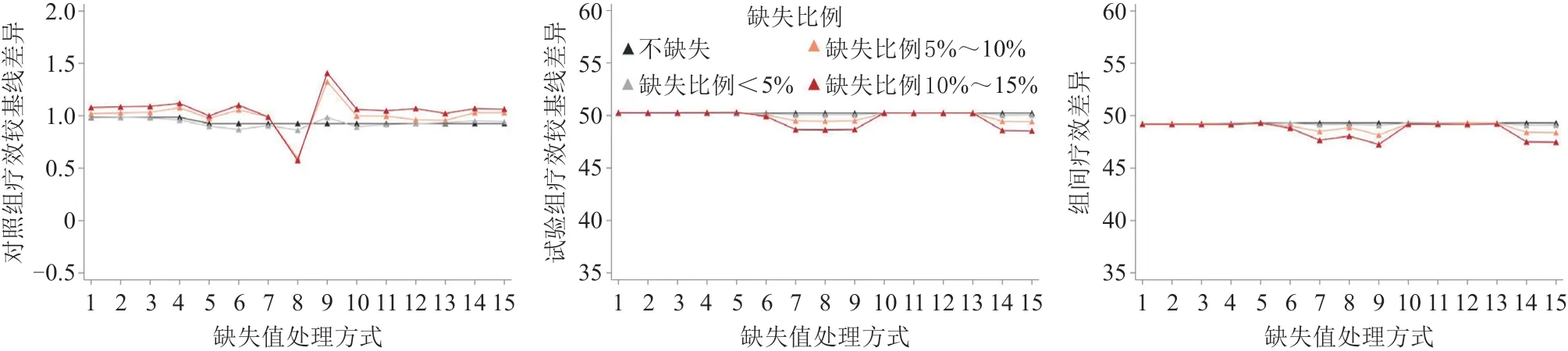
图1 完全随机缺失机制任意缺失模式下不同缺失数据处理方式的比较

2.2 完全随机缺失机制-单调缺失模式 与任意缺失模式比较，单调缺失模式下各处理方式对疗效估计的误差更为明显，见图2。就对照组而言，缺失比例小于5%时的估计误差较小，当缺失率超过5%时，各处理方式均会增加其评估误差，且明显高于任意缺失模式。不同填补方式在试验组中的表现差异明显，各缺失比例下的MMRM与多重填补均不会增加误差且较为稳定，而单一填补方式和模式混合模型则会明显低估疗效，从而大幅增加组间疗效的估计误差。

图2 完全随机缺失机制单调缺失模式下缺失数据不同处理方式的比较

2.3 随机缺失机制-任意缺失模式 在对照组疗效较基线差异的估计中，只有当缺失比例达到10%以上时，各种缺失处理方式均会导致较大误差，见图3。尽管不同缺失数据处理方式在治疗组中均未导致明显的误差，但仍以MMRM和多重填补的表现更为优秀。与此同时，各处理方式对组间疗效差异的估计结果基本稳定一致，提示随机缺失机制-任意缺失模式对缺失值的处理方式并不敏感，各种方式均可用于其缺失数据处理。

图3 随机缺失机制任意缺失模式下缺失数据不同处理方式的比较

2.4 随机缺失机制-单调缺失模式 不同缺失数据处理方式在随机单调缺失模式下的表现见图4，与前述结果类似，随着缺失率的升高，各种处理方式对试验组的疗效估计误差则会越来越大。此外，在众多的缺失数据处理方式中，MMRM对组间疗效差异估计的影响最小，多重填补处理后的ANOVA次之，当缺失比例超过10%时，最差个例分析的误差最大。

图4 随机缺失机制单调缺失模式下缺失数据不同处理方式的比较

3 讨论

通过定期随访的方式追踪受试者药物疗效的变化情况而收集到的由基线特征和多个访视点测量结果构成的纵向数据，是临床试验中最常见的数据类型[6]。而由于访视过程中受试者可能会因为各种原因中途退出，缺失数据的出现成为不可避免的问题。但目前尚未在国内临床研究中引起研究者足够重视，实际应用中，其对缺失数据的处理仍存在盲目应用统计方法的现象，给新药安全有效性的评价和确证带来诸多困难[21]。因此，选择合适的统计学方法分析含有缺失数据的临床试验十分重要。

本研究模拟双臂优效性临床试验，根据三种缺失比例、两种缺失机制以及两种缺失模式设定12种缺失数据集，对每种情形分别采用15种缺失数据处理方式[不同协方差矩阵结构的MMRM模型（非结构化协方差、复合对称协方差、托普利茨协方差、一阶自回归协方差），单一填补（基于末次观测结转、基线观测结转、最差观测结转、最差个例分析）、多重填补（不同填补次数的预测均值匹配与回归）及PMM的ANCOVA]对缺失数据进行处理，并根据不同的疗效估计与真实情况的差异评价各处理方式的统计性能。本研究中我们发现，各种缺失数据处理方式的性能均会受到数据缺失比例、缺失机制及缺失模式的影响，其中缺失比例及缺失模式的影响更为明显。

3.1 不同缺失比例下缺失值处理方式的比较 当缺失比例小于5%时，不同处理方式对疗效估计的结果基本稳定一致，且与真实值差距较小，这与一项国外研究结论相吻合[22]。随着缺失比例的增加，疗效估计产生的误差也越大。当缺失比例大于5%且小于15%时，不论是完全随机缺失机制还是随机缺失机制，任意缺失模式还是单调缺失模式，MMRM与多重填补后进行协方差分析在处理缺失值时均有较优性能，但相比之下前者更为稳定且由于MMRM处理方法无需对缺失数据进行填补，其纳入所有已观测到的数据进行建模分析，符合意向性原则[23]等特点，其在实际研究中可能更具实用价值。多项国外研究也都表明了MMRM较多重填补及以基线观测进行结转的缺失数据处理方式可能更为优越[24-25]。虽然有临床研究者认为当数据缺失超过10%时，统计分析很可能存在偏差而应采用模式混合模型[26]，但本研究发现即使缺失比例大于10%，用模式混合模型依旧低估了药物疗效。这提示在不满足非随机缺失机制的情况下使用模式混合模型对疗效的估计可能不足以反应真实情况。

3.2 不同缺失机制下缺失值处理方式的比较 数据的缺失，究其原因，可以归为三类，即完全随机缺失，随机缺失和非随机缺失[12]。但由于非随机缺失机制中数据的缺失与未观测到数据有关，实际中难以完成模拟，因此，本项研究中只设置了完全随机和随机缺失这两种缺失机制。我们发现，即使采用相同的缺失值处理策略，完全随机缺失机制下估计的效应值要比随机缺失机制下的估计值更接近于真实值。这可能与不同缺失值处理方式有不同适用条件有关，如以末次观测为结转的前提条件之一是数据完全随机缺失[25]。但相比之下，MMRM在完全随机以及随机缺失机制下，均表现最为稳定，这也与其他研究结论相一致[6]。

3.3 不同缺失模式下缺失值处理方式的比较 本研究中，各种缺失数据处理方法在任意缺失模式下与单调缺失模式相比，其疗效估计结果更为稳定。但对于纵向随访的临床试验来说，受试者在某次访视时失访，而其在该次访视之后又继续随访的情况并不多见，因此，临床试验中单调缺失模式下不同缺失值处理方式带来的影响应该更加引起研究者的重视。我们发现，在单调缺失模式下，除MMRM表现较为稳定以外，多重填补后的协方差分析也有较好表现。一项国内研究表明[27]，在单调缺失模式，完全随机缺失和随机缺失机制下，只有线性回归法和预测均值匹配有较好表现。这提示在缺失模式为单调缺失的实际研究中，MMRM或以回归法和预测均值匹配为多重填补的协方差分析应当优先考虑。

虽然目前缺失值处理方法众多，但不同缺失比例，缺失机制以及缺失模式下，采用不同处理策略仍会产生不同偏差，因此，研究者应结合试验的自身特点预先在方案中制定合适的分析策略并进行敏感性分析。在双臂优效性临床试验中，MMRM可能为首选方案。