含夹杂超导体中共线裂纹的相互作用

赵玉峰, 徐 涛

(兰州理工大学 理学院, 甘肃 兰州 730050)

零电阻性和完全抗磁性是超导材料所具有的特性,因此在科研和工业生产等多领域内都有着非常广泛的应用,超导材料一方面可以制成大型器件如超导电缆、超导电机,另一方面可以制成小型精密仪器如超导量子干涉器件,超导计算机等.一般超导复合材料中都存在裂纹和夹杂物,这也已经成为一种普遍现象[1-2].YBCO材料作为超导技术应用的首选材料从室温加工冷却过程中会产生裂纹并影响YBCO超导体的机械能[3].当研究这些材料的断裂行为时[4-6],裂纹与夹杂物之间有着重要的关系.高志文等[7]首先研究了超导体的裂纹问题.Ren等[8]通过研究块体熔融织构YBCO材料在不同温度下的俘获磁场特性为超导体的磁体损伤提供实验数据支持.Gao等[9]研究了Ⅱ型超导体中裂纹与夹杂物之间的关系,并讨论了场冷却后外磁场的问题.Gao等[10]研究了在临界状态Bean模型描述下电磁力作用下的Ⅱ型超导体内共线裂纹的相互作用.张朝霞等[11]研究了外加磁场下REBCO超导体块中平行裂纹的相互作用.Xue等[12]研究了椭圆形夹杂物对临界电流密度的影响,结果表明夹杂物的存在导致临界电流密度明显降低.Xue等[13]研究了电磁力作用下超导块体中斜向裂纹与圆形夹杂物之间的关系.Zhao等[14-15]研究了具有非均匀临界电流分布的长圆柱型超导体的裂纹夹杂一般问题.Zhao等[16]考虑非均匀超导体的电流密度与空间相关的俘获磁通特性.刘俊杰[17]和郭俊宏等[18]研究了夹杂物变硬或者带孔的特殊情况.以上研究并没有考虑夹杂物与两个或者两个以上裂纹之间的影响,而夹杂双裂纹之间是有显著影响的.

本文研究了高温超导体在外加磁场与粘性磁通量流动的共同作用下含夹杂物的共线裂纹的断裂行为,同时还比较了裂纹长度与夹杂物对应力强度因子的影响.电磁行为由临界状态(Bean模型)描述,圆形夹杂物和裂纹对临界电流密度造成的扰动假定可以忽略不计,在该模型中不予考虑.

1 几何模型和基本方程

如图1所示放置在外磁场Ba中的一个宽为2w的无限长超导平板,在平板中心有一个半径为r的圆形夹杂物,在平板中心处,沿y轴有两个长度为2a的共线裂纹,d代表夹杂物中心到裂纹的距离,超导基体和夹杂物的弹性模量不同,分别用E1和E2表示.在块状体裂纹部分,电流回路完全破坏,没有电流通过该区域.本文的断裂问题基于以下假设：1) 忽略裂纹和夹杂物对屏蔽电流的干扰；2) 由于忽略磁效应和低临界场.可将其视为平面应变问题；3) 假设超导体是线弹性的.

图1 含有夹杂-共线裂纹的超导体Fig.1 Superconductor plate with inclusion collinear crack

在当前超导体板模型中,根据临界状态Bean模型.电磁场中的磁通钉扎力可以用以下形式给出：

(1)

讨论零场冷却条件下外磁场下降阶段的超导体内磁场分布,超导体板内磁通分布如下：

(2)

式中：B为超导体板中的磁场；Jc为临界电流密度；根据Bean模型等于常数.η为与磁通运动相关的粘度；v为局部磁通速度；φ0为磁通量子；μ0为真空磁导率.∓表示增加或减小磁场的超导体的磁通运动或离开.

超导体板内的磁通连续性方程表示如下：

(3)

根据Liu等[19]的研究结果,本文假设：B(x,t)=B(δ),δ=x-v0t,v0是超导体板内恒定通量流速.得到v=v0时,B(x-v0t)是式(3)的解.将超导体板沿厚度方向对x积分可以得到应力表达式：

(4)

当外磁场从最大值Bm逐渐下降到Ba时,超导板体内部的磁通密度分布可以表示为

外磁场的下降率dBa/dt与v0有关,dBa/dt=-μ0[Jc+(ηv0/φ0)]v0，v0表示恒定速率,并假设η和φ0.通过式(5),当x=x0时板体内磁通被分成激活区域和非激活区域；当xx0时,该区域处于活动状态.

通过Bp=μ0Jcw将Bm,Ba,Bx进行正则化：

(8)

含夹杂共线裂纹尖端的应力强度因子值能作为判断超导材料断裂性能的重要依据,而J积分表示含夹杂共线裂纹尖端的应力强度因子,在本模型中应用平面应变法J积分表示为

(9)

式中:Γ为裂纹底端开始到裂纹顶端结束的积分围线;W为超导板体内应变能密度；Ti为作用在超导板体上的张力矢量；u是超导板体上的位移矢量.

在平面应变条件下计算J积分值与应力强度因子K1之间的关系：

(10)

式中:ν是泊松比，ν=0.3；E为杨氏模量,E=80 GPa.进行无量纲处理.目的是将运算过程尽量简单化：

(11)

式中

(12)

2 结果及分析

图2展示了裂纹A端应力强度因子随着外磁场从4Bp减小到0过程中变化情况.随着外磁场逐渐减小,图中假设的三种磁通粘滞流动速率下的应力强度因子在初始阶段迅速增加,大约在Ba=2Bp处达到峰值,之后增大趋势放缓,在2Bp到0这个阶段内,应力强度因子值缓慢下降,磁通粘滞流动速率越大其下降程度越缓慢,且粘滞磁通速率越大含夹杂共线双裂纹尖端处应力强度因子的峰值出现在外磁场Ba越小处.

图2 不同磁通粘滞速率下Ba/Bp对K1/K0的影响Fig.2 Effect of Ba/Bp on K1/K0 under different flux viscosity rates

图3描述了夹杂半径r/w对应力强度因子K1/K0的影响.从图中可以看出随着裂纹长度增长,应力强度因子K1/K0也逐渐减小,说明两者之间负相关.同时可以看出在相同裂纹长度情况下,远离夹杂的裂纹端A和D与靠近夹杂的裂纹尖端B和C之间的应力强度因子值几乎是相同的,同时B和C端要小于A和D端的应力强度因子值,从图中可以得出夹杂半径r越大对含夹杂共线裂纹尖端应力强度因子的抑制作用也就越强.

图3 r/w对裂纹尖端K1/K0的影响Fig.3 Effect of r/w on crack tip K1/K0

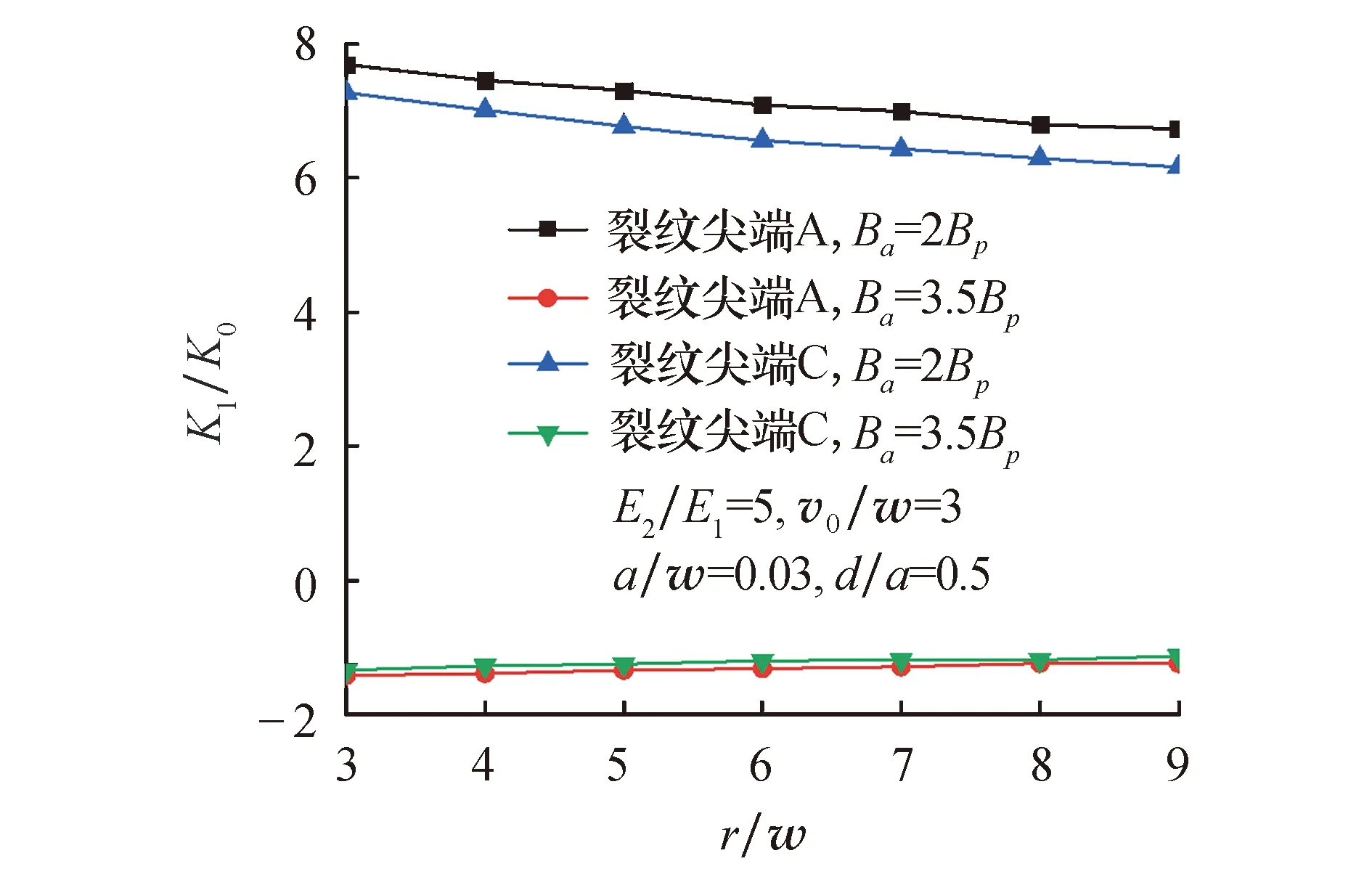
图4描述了不同的弹性模量E2/E1对应力强度因子K1/K0的影响.由图可知随着夹杂与基体弹性模量比值E2/E1的增大,应力强度因子K1/K0逐渐减小,说明两者之间负相关.在E2/E1<1之前,随着E2/E1的增大,应力强度因子快速下降,且在0

图4 E2/E1对裂纹尖端K1/K0的影响Fig.4 Effect of E2/E1 on crack tip K1/K0

图5描述了a/w对裂纹尖端A和C处在Ba=2Bp,Ba=3.5Bp两种情况下对应力强度因子K的影响.在外部磁场激励过程中,对于不同的外部磁场条件,当Ba=3.5Bp时,应力强度因子K1/K0<0,此时整个超导体受压,产生压缩裂纹,在这种情况下a/w与K1/K0正相关,当Ba=2Bp时，应力强度因子K1/K0>0,超导块体受拉而产生裂纹,在这种情况下a/w与K1/K0负相关.

图5 外磁场下降过程中a/w对不同处裂纹尖端K1/K0的影响Fig.5 Effect of a/w on crack tip K1/K0 at different places during the decrease of external magnetic field

图6描述了a/w对裂纹尖端A和C处在v0/w=2,v0/w=3两种情况下对应力强度因子K1/K0的影响.如图可见,a/w与K1/K0正相关.v0/w=3时,裂纹尖端C处应力强度因子值要大于v0/w=2时裂纹尖端A处的值,说明夹杂对裂纹尖端的影响要明显小于粘性磁通量流速v0对裂纹尖端的影响.

图6 不同粘性磁通量流速下a/w对裂纹尖端K1/K0的影响Fig.6 Effect of a/w on crack tip K1/K0 under different viscous flux flow rates

图7描述了r/w对裂纹尖端A与C处在Ba=2Bp,Ba=3.5Bp两种情况下对应力强度因子K1/K0的影响.逐渐增大的夹杂半径r会缓慢抑制应力强度因子K1/K0的扩展,处于不同外界磁场条件下的裂纹尖端有着明显的差别.在外磁场下降初始阶段会抑制裂纹的扩展,随着外磁场不断下降这种抑制作用会减弱.

图7 外磁场下降过程中r/w对裂纹尖端K1/K0的影响Fig.7 Effect of r/w on crack tip K1/K0 during the decrease of external magnetic field

图8描述了r/w对裂纹尖端A和C处在v0/w=2与v0/w=3两种情况下对应力强度因子K的影响.如图可见,r/w与K1/K0负相关.v0/w=3时裂纹C端应力强度因子大于v0/w=2时裂纹A端应力强度因子的比值,说明粘性磁通量流速v0对裂纹尖端应力强度因子的促进作用强于夹杂对裂纹尖端应力强度因子的抑制作用.

图8 不同粘性磁通量流速下r/w对裂纹尖端K1/K0的影响Fig.8 Effect of r/w on crack tip K1/K0 at different viscous flux flow rates

图9展示了在不同磁通粘滞流动速率v0/w下,A和 C处裂纹尖端与夹杂物的距离d/a对共线裂纹尖端应力强度因子K1/K0的影响.当夹杂物与裂纹之间的距离比较近时(d/a<2)A和C处裂纹尖端应力强度因子K1/K0都迅速增加,夹杂对于C处应力强度因子的抑制强于A处；在夹杂物与裂纹之间的距离比较远时,含夹杂共线裂纹尖端处应力强度因子值的增长速率逐渐放缓,可以预见的是，当本模型中裂纹尖端与夹杂物之间的距离足够远时,A和C处裂纹尖端应力强度因子K1/K0几乎相等.通过对比,发现当夹杂物与裂纹尖端d/a处于某一定值时,磁通粘滞流动速率v0/w越快,裂纹尖端应力强度因子K1/K0越大.随后都慢慢趋于定值.

图9 外磁场下降过程中K1/K0随d/a的变化

3 结论

本文基于 Bean模型提出了一个解决超导体中具有中心夹杂的共线双裂纹的理论模型，其中不考虑夹杂物和裂纹对屏蔽电流的扰动，忽略磁效应和低临界场.结果表明：外磁场，裂纹长度，以及夹杂物尺寸等因素都对超导体板的裂纹有着明显的影响，夹杂物能明显抑制裂纹近端处(B和C端)应力强度因子值的大小，超导体基体与夹杂的杨氏模量之比对裂纹影响非常剧烈，尤其是弹性夹杂能明显抑制基体裂纹的扩展.