内置不同型钢的钢管混凝土组合构件横向冲击性能

党利荣, 刘新文, 张林芝, 曹旭东, 祁生旺

(1. 甘肃第四建设集团有限责任公司, 甘肃 兰州 730060; 2. 甘肃建投科技研发有限公司, 甘肃 兰州 730050)

在钢管混凝土中配置型钢或钢管等,可以显著提高该类组合构件的承载力,改善构件力学性能[1-3]；截面尺寸相同时,该类构件比钢管混凝土有更高的承载力和更好的延性,常被用作超高层结构或大跨结构中承受重载的构件.对于内置型钢钢管混凝土,内部型钢受到混凝土的保护,型钢的存在使得该类构件的承载性能明显提高[4-5].图1为三种不同截面形式的内置型钢钢管混凝土组合构件,包括内置十字形型钢(构件CC)、内置工字形型钢(构件CI)和内置L形角钢(构件CL)组合构件.

图1 内置型钢钢管混凝土组合构件截面形式(mm)Fig.1 Sectional form of steel-reinforced CFST composite specimens(mm)

钢管混凝土及其组合构件在使用过程中往往面临着冲击荷载的威胁,如交通工具对站台柱的冲击、船舶对桥墩的冲击以及人为因素造成的冲击等.冲击荷载会引起结构构件变形,甚至造成结构倒塌,因此对结构构件的抗冲击性能研究十分必要.目前,研究者对钢管混凝土构件的横向冲击性能进行了较多的研究,Wang等[6]对钢管混凝土构件在侧向冲击作用下的动力响应进行了试验研究和有限元分析；Aghdamy等[7]运用数值方法对中空夹层钢管混凝土柱的侧向冲击响应进行了分析；章琪等[8]利用ABAQUS对冲击荷载作用下不同类型的钢管混凝土构件进行了数值模拟；Yousuf等[9]对不锈钢管混凝土试件在静态荷载和冲击荷载作用下的力学性能进行了试验研究.但目前对于内置型钢或钢管的钢管混凝土组合构件抗冲击性能研究相对较少,朱翔等[10]对不同截面的新型复合柱进行横向冲击试验和数值模拟,包括内置圆钢管和内置十字形型钢的钢管混凝土组合构件；史艳莉等[11]采用有限元方法对内置圆钢管的圆钢管混凝土构件的横向冲击过程和影响因素进行了分析；Xian等[12]对内置型钢的圆钢管混凝土构件横向冲击过程进行了试验研究.因此有必要对内置型钢钢管混凝土构件的横向冲击过程进行进一步研究,分析不同截面组合构件的抗冲击性能,以及内置型钢参数变化对构件抗冲击性能的影响,以期为相关工程设计提供参考.

本文建立了三种不同内置型钢钢管混凝土构件的横向冲击有限元模型,通过已有组合构件的横向冲击试验对模型的正确性进行了验证.对比了内置三种型钢对钢管混凝土构件抗冲击性能的影响,分析了组合构件冲击过程中的跨中挠度、冲击力和截面弯矩发展,以及构件的变形.最后讨论了不同型钢参数变化对组合构件抗冲击性能的影响.

1 材料本构

1.1 钢材

钢材采用文献[13]中提出的五段式弹塑性本构关系.在动态冲击荷载作用下,采用Cowper-Symonds模型[14]计算钢材在冲击荷载作用下的动态屈服强度,计算公式如下式：

(1)

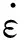
1.2 混凝土

混凝土采用塑性损伤模型,其本构关系采用文献[13]中适用于圆钢管混凝土中核心混凝土的应力-应变关系.混凝土在动态荷载作用下的应变率采用CEB-FIP中的模型计算[14],对于抗压强度,计算公式如下：

(2)

(3)

式中:ftd和fts分别为混凝土动态加载时和静态加载时的抗拉强度[14],静态加载时的应变率取1×10-6s—1,δ和β为参数,logβ=6δ-2,δ=1/(1+8f′c/10).

2 有限元模型

2.1 模型建立

在ABAQUS有限元软件中建立构件的横向冲击数值模型,包括内置十字形型钢(CC)、内置工字形型钢(CI)和内置角钢(CL)的钢管混凝土构件,截面尺寸如图1,三种构件长度为1 600 mm,型钢厚度均匀,构件的型钢含钢率相同(即型钢横截面面积与混凝土横截面面积之比相同).钢材和型钢屈服强度为345 MPa,混凝土抗压强度为50 MPa.模拟时钢管、混凝土和端板均为C3D8R的三维实体单元,型钢采用壳单元(S4R).落锤采用刚体模拟,矩形落锤尺寸参考文献[12]取80 mm×200 mm,质量为1 000 kg,冲击速度为8 m/s.图2为构件CI的边界与网格划分,网格大小为15mm,通过约束端板三个方向的位移和转角实现固支边界.

图2 构件CI的边界与网格Fig.2 Boundary and mesh of the member CI

2.2 模型验证

对已有圆钢管混凝土和内置型钢圆钢管混凝土构件横向冲击试验进行模拟,包括试件的跨中挠度时程曲线和冲击力时程曲线,以验证文中横向冲击数值模型的合理性.试件参数如表1,表中截面尺寸为试件的外直径和钢管壁厚.内置型钢钢管混凝土和钢管混凝土试件的净跨分别为1 100 mm和2 000 mm,内置十字形型钢和工字形型钢的腹板高度和翼缘宽度相同,分别为100 mm和40 mm,二者壁厚均为3 mm.

表1 横向冲击试件信息与结果

钢管混凝土在横向冲击荷载作用下,其跨中挠度和冲击力平台值是衡量构件抗冲击性能的重要指标,因此其计算的准确性是反映构件冲击过程模拟准确性的重要表现.图3为试验跨中挠度时程曲线和模拟曲线对比.可以看出,二者吻合较好,跨中最大挠度试验值与模拟值之比的平均值为1.02.图4给出了冲击力时程曲线试验结果和模拟曲线对比,冲击力时程曲线整体吻合较好,试验的冲击力平台值与模拟值之比的平均值为1.03.综上可见,文中数值模型计算结果与试验结果整体吻合良好,表明数值模型计算结果准确.

图3 跨中挠度时程曲线对比

图4 冲击力时程曲线对比

3 组合构件冲击过程分析与对比

3.1 跨中挠度时程曲线

图5为不同组合构件的跨中挠度时程曲线,同时给出未配置型钢的钢管混凝土构件(构件C)作为对比.可见,对于组合构件,构件CI的跨中挠度最小,构件CC的最大,而构件CL介于二者之间,且组合构件的跨中挠度明显小于钢管混凝土构件.这表明型钢的存在可以明显减小钢管混凝土构件的整体变形,当型钢含钢率相同时,内置工字形型钢对钢管混凝土构件抗变形能力提升效果最显著.这可能是因为型钢含钢率相同时(型钢也壁厚相同),内置工字形钢的腹板更高,整体抗弯能力更强.如构件C的跨中最大挠度为88.6 mm,内置十字形型钢、工字形型钢和L形角钢后,构件的跨中最大挠度分别减小了13%、27%和21%.

图5 构件的跨中挠度时程曲线对比 Fig.5 Comparison of time history curves of mid-span deflection of specimens

3.2 冲击力时程曲线

图6为不同组合构件的冲击力时程曲线.可以看出,组合构件的冲击力时程曲线与钢管混凝土构件相似,其冲击过程可分为震荡阶段(OB)、平台阶段(BC)和卸载阶段(CD)[13].在OB阶段,冲击力达到峰值后迅速减小并震荡,到B点时稳定；在BC阶段,冲击力保持相对稳定,波动很小,该阶段的冲击力平台值是反映构件抗冲击能力的直接表现[6,14]；C点后冲击力迅速减小,到D点时冲击力为0 kN,落锤与组合构件发生分离.对比可见,在钢管混凝土中分别内置十字形型钢、L形角钢和工字形型钢后,构件的冲击力平台值逐渐提高,冲击持续时间缩短,这表明构件的抗冲击能力增强.如构件CC、CL和CI的冲击力平台值分别为397.6、460.6、418.8 kN,冲击持续时间分别为24.8、21.8、23.6 ms,与钢管混凝土构件C相比,冲击力平台值分别提高了20%、40%和27%,冲击时程缩短了13%、24%和17%.可见型钢含钢率相同时,内置工字形型钢对构件抗冲击能力的提升最显著.

图6 构件的冲击力时程曲线对比Fig.6 Comparison of time history curves of impact force of specimens

3.3 弯矩时程曲线

在ABAQUS前处理中创建构件不同部件的跨中横截面,通过后处理中的自由切片获得组合构件不同部件的弯矩时程曲线.图7为不同组合构件跨中截面的弯矩时程曲线.可以看出,当冲击力达到峰值时,弯矩几乎也达到最大,并出现小幅震荡；在平台阶段,弯矩逐渐均匀降低,但降低幅度较小；进入卸载阶段,弯矩迅速降低.由于落锤与构件分离后构件发生震动,因此弯矩在D点后维持在较低水平波动.与钢管混凝土构件相比,组合构件的整体截面弯矩均提高,这表明构件整体抗弯能力提升.与钢管混凝土相比,在B点时,构件CC、CI和CL的截面弯矩分别提高了9%、37%和21%,可见内置工字形型钢对构件弯矩的提升最显著.

图7 构件的跨中截面弯矩时程曲线对比Fig.7 Comparison of time history curves of sectional moment of members

3.4 各部件的弯矩发展与分布

以构件CI为例,分析组合构件在冲击过程中各部件对抗弯能力的贡献,图8a为构件CI各部件的跨中截面弯矩时程曲线.可见,整个冲击过程中,钢管承担的弯矩最多,混凝土次之,型钢承担的最少.这是因为钢管受到混凝土的支撑作用，性能发挥更充分,同时钢管含钢率也大于型钢的含钢率.此外,在平台阶段,钢管和型钢的截面弯矩保持稳定,而混凝土的截面弯矩逐渐降低,表明内置型钢组合构件截面弯矩降低主要由混凝土承载力降低引起,钢管和型钢受到混凝土的支撑作用,性能发挥充分.

图8b为组合构件各部件在B点时承担的截面弯矩占比.可以看出,对于三种不同的组合构件,钢管承担的弯矩均为最高,型钢承担的最少,钢管与型钢承载的弯矩占比不同,而混凝土承担的弯矩相近,这表明内置型钢的截面形式对组合构件的弯矩分布影响显著.虽然不同组合构件的截面弯矩不同,但混凝土承担的弯矩占比相近,这是因为型钢对混凝土的约束作用影响其抗弯能力.如构件CC、CI和CL在B点时钢管承担的截面弯矩分别为46.1、45.8、46.5 kN·m,混凝土承担的分别为24.6、30.9、26.6 kN·m,可见钢管承担的弯矩大小没有明显变化,而混凝土的截面弯矩改变,这表明型钢含钢率相同时,型钢截面形式对混凝土的约束作用影响明显.

图8 构件截面弯矩发展与分布Fig.8 Development and distribution of sectional moment of members

3.5 组合构件的变形

图9给出组合构件外钢管与型钢的变形.不同组合构件钢管的变形相似,如图9a所示,钢管整体产生了弯曲变形,在跨中冲击位置产生了局部凹陷；构件两端下部受压产生了局部鼓曲变形,而跨中与两端之间的钢管没有明显局部屈曲,钢管应力较高区域也主要集中在跨中和两端,这表明钢管受损区域主要在跨中和两端.图9b为不同截面型钢的整体变形,可以看出,型钢均产生了整体弯曲,但未出现局部屈曲变形,这是因为型钢受到混凝土的支撑作用.这表明型钢与混凝土相互影响,二者性能发挥得更充分.

图9 外钢管和型钢的破坏形态

图10为构件CI钢管和型钢的等效塑性应变和混凝土的纵向截面的应变.可见钢管和型钢的塑性变形区域均在跨中和两端,而跨中与两端之间的范围没有产生塑性变形,混凝土在跨中下部和两端的上部产生较大的拉应变,跨中与两端之间的应变较小.这表明在横向冲击荷载作用下,构件在跨中冲击位置和两端产生了明显的损伤.

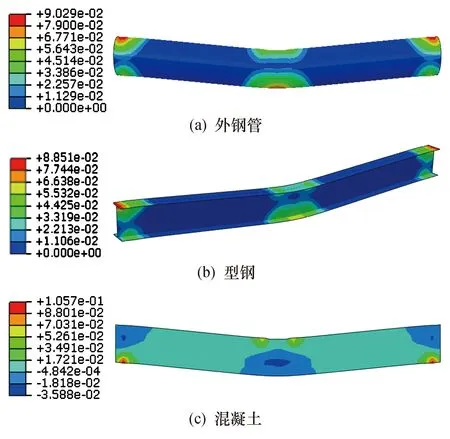
图10 构件CI的等效塑性应变和纵向应变

4 影响因素分析

4.1 型钢的开展程度

第3节分析结果表明当含钢率相同时(型钢的壁厚相同),内置工字形型钢组合构件的抗冲击能力优于内置十字形型钢组合构件,这可能与型钢的开展程度(型钢腹板高度)有关,型钢含钢率相同时,工字形截面型钢比十字形型钢截面更开展.保持构件CC型钢含钢率以及翼缘与腹板的高宽比不变,通过改变型钢的厚度和腹板高度分析型钢开展程度对构件抗冲击能力的影响.图11为型钢腹板高度对构件跨中挠度和冲击力平台值的影响.可见,当型钢含钢率不变时,随着型钢腹板高度的增加,构件的跨中最大挠度和残余挠度均逐渐减小,冲击力平台值逐渐增大,这表明型钢越开展(腹板越高),构件的抗冲击能力越强.

图11 型钢腹板高度对挠度和冲击力的影响Fig.11 The effect of the profiled steel web height on the deflection and impact force

4.2 角钢的分布位置

对于内置L形角钢的构件,保持型钢含钢率不变,改变角钢距钢管外边缘的距离d,以分析角钢的分布位置对构件的抗冲击性能的影响.图12a为角钢分布位置对跨中挠度的影响.可见,随着d的减小,跨中最大挠度和残余挠度均减小.这表明角钢越靠近钢管,构件的变形越小.图12b为角钢分布位置对冲击力平台值的影响,可以看出,角钢越靠近外钢管,冲击力平台值越高,如当d从35 mm减小到10 mm时,冲击力平台值增大了38.3 kN.综上可见,当型钢含钢率不变时,L形角钢的分布位置对构件的抗冲击性能有一定影响,角钢越靠近外钢管,构件的抗冲击性能越强.

图12 角钢分布位置对挠度和冲击力的影响Fig.12 The influence of distribution position of angle steel on the deflection and impact force

4.3 角钢的肢长

保持型钢含钢率不变,角钢与钢管外表面距离为15 mm,改变角钢肢长,分析角钢肢长变化对构件抗冲击性能的影响,构件编号中数字分别代表肢长和厚度.图13为角钢肢长变化对构件跨中挠度和冲击力的影响.可以看出,当型钢含钢率不变时,肢长变化对构件跨中挠度时程曲线和冲击力时程曲线影响很小,肢长不同构件的曲线几乎重合,这表明角钢肢长变化对构件抗冲击性能影响不明显.

图13 角钢肢长变化对挠度和冲击力的影响Fig.13 The influence of change of angle steel leg length on the deflection and impact force

4.4 型钢翼缘的宽厚比

4.1节分析表明对于内置十字形型钢的组合构件,型钢越开展,对抗冲击性能越有利.保持腹板高度为120mm,型钢含钢率不变,改变型钢翼缘的宽度,分析翼缘宽厚比变化对组合构件抗冲击性能的影响.图14为型钢宽厚比变化对构件挠度和冲击力的影响,构件编号中数字分别代表型钢翼缘宽度和厚度.可见,当型钢含钢率不变时,翼缘宽厚比变化对构件跨中挠度时程曲线和冲击力时程曲线影响较小,随着宽厚比增加,跨中挠度呈略微减小趋势,冲击力平台值略有提高,表明翼缘宽厚比变化对构件抗冲击性能影响很小.

图14 型钢宽厚比对挠度和冲击力的影响Fig.14 The influence of the width-thickness ratio of profiled steel on deflection and impact force

4.5 型钢的含钢率

保持三种组合构件的型钢位置不变,通过改变型钢的壁厚来改变构件的型钢含钢率,以分析型钢含钢率变化对构件跨中最大挠度和冲击力平台值的影响.构件CC和CI的腹板高度和翼缘宽度相同,分别为120 mm和80 mm；构件CL角钢的肢长为35 mm,角钢与钢管外表面距离为15 mm.图15a为型钢含钢率对构件跨中最大挠度的影响.可见,不同组合构件的跨中最大挠度均随着型钢含钢率的增加而减小,其中构件CI降低更明显,这表明增加型钢含钢率可以提高组合构件的抗变形能力.如当型钢含钢率从0.037增加到0.077时,构件CC、CI和CL的跨中最大挠度分别降低了13%、18%和14%.图15b为型钢含钢率对构件冲击力平台值的影响.可以看出,不同组合构件的冲击力平台值均随着型钢含钢率的增加而提高,其中构件CI增加得最显著.当型钢含钢率从0.037增加到0.077时,构件CC、CI和CL的冲击力平台值分别提高了17%、25%和17%.综上可见,增加型钢的含钢率可以减小组合构件在横向冲击荷载作用下的整体变形,提高构件的抗冲击性能.

图15 型钢含钢率对挠度和冲击力的影响Fig.15 The influence of profiled steel ratio on deflection and impact force

4.6 冲击角度

以CI构件为例,保持落锤速度和大小不变,改变冲击速度方向,以分析冲击角度对构件撞击性能的影响,图16为冲击角度对构件挠度和冲击力的影响.可见,随着冲击角度增大,构件的跨中挠度显著增加,冲击力峰值降低,平台阶段和冲击力时程变短,这表明90°冲击构件时最不利.当冲击角度从30°增加到90°(冲击速度与构件轴线垂直),跨中最大挠度增加了243%,冲击持续时间增加了43%.可见冲击角度对构件抗冲击性能影响显著,因此进行冲击分析时应该合理考虑冲击角度.

图16 冲击角度对挠度和冲击力的影响 Fig.16 The influence of angle of impact load on the deflection and impact force

5 结论

1) 在钢管混凝土中内置型钢可以减小构件在横向冲击荷载作用下的整体变形,提高构件的抗弯能力和抗冲击性能.当型钢含钢率相同时,内置工字形型钢的组合构件抗冲击性能最佳.

2) 整个冲击过程中,钢管承担的弯矩最高,混凝土的次之,型钢承担的最小.内置型钢的截面形式对组合构件的弯矩分布影响显著,平台阶段组合构件的截面弯矩降低主要是由混凝土承载力降低引起.

3) 横向冲击后组合构件在跨中和两端产生明显的变形和损伤.型钢的开展程度对构件的抗冲击性能影响明显；当型钢含钢率不变时,构件的抗冲击能力随着型钢腹板高度的增加逐渐提高,开展的型钢截面形式对构件的抗冲击性能更有利.

4)角钢的分布位置对构件的抗冲击性能有一定影响,角钢越靠近外钢管,组合构件的抗冲击性能越强.当型钢含钢率不变时,角钢的肢长和型钢的宽厚比变化对构件的抗冲击性能影响很小.

5) 不同截面内置型钢钢管混凝土组合构件的抗冲击性能随着型钢含钢率的增加而提高,且型钢含钢率变化对内置工字形型钢组合构件影响更显著；冲击角度对构件抗冲击性能影响显著.