致密油藏多重介质非线性渗流压力响应分析

康 浩, 李林凯, 高 建, 侯美伶, 刘胜利, 张继敏

(1. 河北师范大学 中燃工学院, 河北 石家庄 050024; 2. 西南石油大学 油气藏地质及开发工程国家重点实验室, 四川 成都 610500; 3. 西南石油大学 石油与天然气工程学院, 四川 成都 610500; 4. 中国石油勘探开发研究院, 北京 100083)

随着常规油气藏开发潜力的降低以及全球能源需求的增加，非常规油气藏逐渐受到大家的重视[1-3].致密油是继页岩气之后全球非常规油气勘探开发的又一新热点，将会是未来重要的石油接替能源[4-7].由于致密储层孔隙度和渗透率极低，一般采用水平井多段水力压裂方法以达到经济产能.在压裂过程中，创造人工裂缝的同时，开启次级裂缝，最终形成强非均质性的复杂缝网.压裂缝网中主裂缝、次级裂缝以及致密基质构成了致密油藏复杂的渗流系统.国内外学者针对致密储层油气渗流做了大量的工作，提出了各种数学模型，主要有径向三孔模型[8]、线性模型[9-11]、复合模型[12]等，在此基础上，本文考虑油气在致密储层基质中的非线性渗流特点，建立非线性试井解释模型，分析裂缝及储层参数对压力响应的影响规律，为致密储层的评价提供技术支持.

1 低速非达西渗流新模型

致密油藏储层微纳米孔隙普遍发育，由于岩石与流体之间的强烈的相互作用，流体在微纳米孔隙中心与孔壁处表现出不同性质，流体粘度从孔隙中心到孔壁逐渐增加，孔隙半径越小，这种效应越明显.室内实验和分子动力学模拟均表明，油气在致密储层中渗流呈现出低速非达西渗流的特点.目前描述低速非线性渗流的模型有拟启动压力模型、分段模型、连续模型、分形模型等，其中，姜瑞忠等[13]基于毛细管模型和边界层理论，建立了具有物理背景的二参数连续模型：

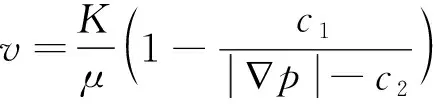
(1)

式中：v为渗流速度，cm/s；K为绝对渗透率，μm2；μ为流体粘度，mPa·s；∇p为压力梯度，0.1 MPa/cm；c1和c2反映了启动压力梯度和非线性渗流的特征参数，0.1 MPa/cm；当c1=0时，该模型退化成达西模型，当c2=0时，该模型变成拟启动压力梯度模型.由式(1)可知，最小启动压力梯度为∇pmin=c1+c2，当压力梯度小于该值时，流体不流动.关于启动压力梯度是否存在仍存在争议，部分学者认为启动压力梯度是由于实验仪器精度、毛管效应及岩心的麻皮效应(麻皮效应为由于岩心样品表面的粗糙坑凹、拐角和棱线等部位所造成的岩心渗流实验的误差)等造成的假象，是不存在的.Wang等[14]明确指出启动压力梯度不存在，此时上述模型变为

(2)

式中：c是实验拟合参数，0.1 MPa/cm.利用式(2)拟合Ren等的实验数据如图1所示[15]，拟合结果为

图1 低速非达西新模型实验拟合图

v=0.0033[1-0.1063/(|∇p|+0.106 3)]∇p，拟合系数R2=0.998 1，表明该模型能够很好地描述致密储层的渗流规律.

2 数学模型

如图2所示，基于多重介质理论，将致密油藏划分为三重介质：(1) 渗透率高、储存空间小的大裂缝系统；(2) 中等渗透率和储存空间的介质，包含微裂缝和致密介质中的大孔隙；(3) 渗透率和孔隙度最小的致密基质.假定流体在介质(1)和(2)中符合达西渗流，在介质(3)中遵循低速非达西渗流，考虑井筒储存和表皮效应的影响，建立数学模型如下：

初始条件：

pm(r,0)=pf(r,0)=pF(r,0)=pi

(6)

内边界条件：

(7)

封闭外边界：

(8)

定压外边界：

pF|r=re=pi

(9)

图2 致密油藏多重介质模型

式中:KF、Kf和Km分别为大裂缝渗透率，微裂缝渗透率和基质渗透率；PF、Pf和Pm分别为大裂缝系统压力，微裂缝系统压力和基质系统压力；φF、φf和φm分别为大裂缝系统孔隙度、微裂缝系统孔隙度和基质系统孔隙度；ctF、ctf和ctm分别为大裂缝系统压缩系数、微裂缝系统压缩系数和基质系统压缩系数；σf、σm分别为大裂缝与基质窜流系数、大裂缝与基质的窜流系数；pw为井底流压；pi为原始地层压力；C为存储系数；s为表皮系数；rw为井筒半径；re为边界半径；h为储层厚度.

则上述模型变为

初始条件：

pmD(rD,0)=pfD(rD,0)=pFD(rD,0)=0

(13)

内边界条件：

(14)

封闭外边界：

(15)

定压外边界：

pFD|rD=reD=0

(16)

3 模型求解及验证

采用有限差分方法，做坐标空间变换rD=ex，划分m个网格，令Δx=lnreD/(m-1)，Mi=Δx2/Δt·ωFe2(i-1)Δx-2s，Nfi=λfe2(i-1)Δx-2sΔx2，Nmi=λme2(i-1)Δx-2sΔx2，建立数值模型如下：

内边界条件：

(20)

封闭外边界：

(21)

定压外边界：

(22)

按照式(17)～式(22)组装非线性代数方程组，采用牛顿-拉普生迭代法求解.求解过程中，每个迭代步更新δD，编制相应程序.图3是在达西渗流条件下解析解与数值解对比图(其中，平滑线为解析解，离散点为数值解)，其中，CDe2s=100，ωF=0.05，ωf=0.2，ωm=0.75，λfe-2s=10-5，λme-2s=10-6.由此可以证明所编程序的正确性.

图3 达西模型下数值解与解析解对比图

4 结果分析

采用以上计算方法，分别计算各参数对试井曲线的影响如下：

图4是不同非线性渗流参数c对压力及压力导数曲线的影响，由图4可知，非线性渗流参数主要影响第二个凹子的位置和深度，随着参数的增大，凹子的深度变小而且出现的时间后移，表明基质的非线性参数主要影响了裂缝与基质之间的物质交换.

图4 非线性渗流参数对试井曲线的影响Fig.4 Influence of nonlinear flow parameter

图5是窜流系数对试井曲线的影响，λfe-2s代表了大裂缝与小裂缝之间的窜流情况，λme-2s代表了大裂缝与基质之间的窜流情况.由图5可知，当两个窜流系数相等时，大裂缝与小裂缝、大裂缝与基质之间的窜流能力相同，在压力导数曲线上只出现一个凹子.当两者不同时出现两个凹子，而且随着窜流系数的增加，对应的凹子深度减小.

图5 窜流系数对试井曲线的影响

图6是弹性储容比对试井曲线的影响，由图6可知，微裂缝储容比ωf的增加使第一个凹子的深度加大，而基质储容比ωm的增加同时加深了两个凹子的深度.

图6 弹性储容比对试井曲线的影响Fig.6 Influence of cross flow coefficients

图7是不同边界条件对试井曲线的影响规律.由图7可知，当压力波未传到边界，压力导数曲线趋近于0.5水平线，呈现出径向流的特征；当压力波传到封闭边界时，压力导数曲线上表现为上翘；当压力波传到定压边界时，压力导数曲线表现为下弯.

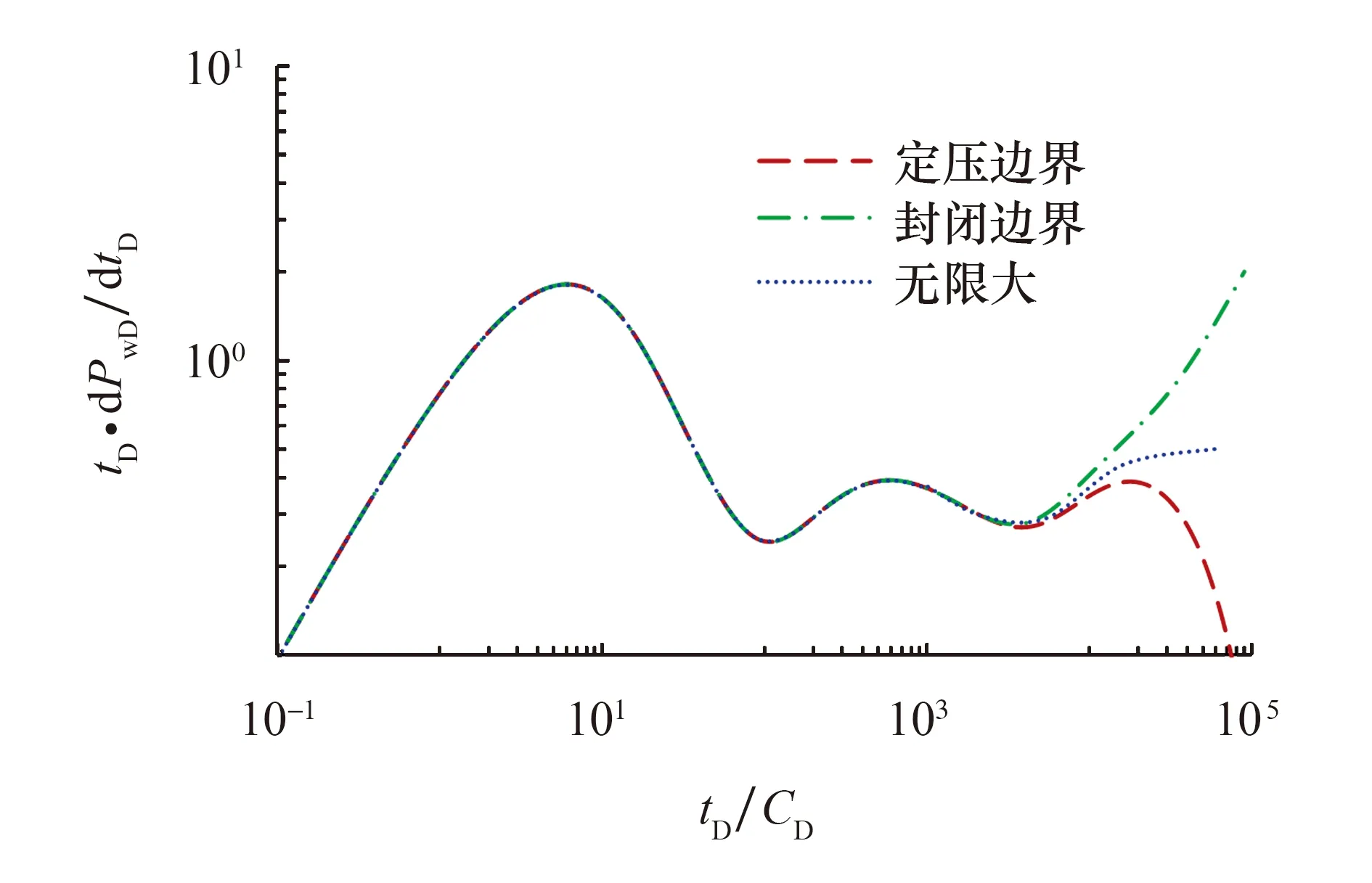
图7 边界条件对试井曲线的影响Fig.7 Influence of boundary conditions

5 结论

1) 通过分析致密油藏渗流介质特点，建立了考虑基质非线性渗流的致密油藏多重介质数学模型，运用牛顿-拉普生迭代法求得了模型的数值解，并验证了模型的正确性.

2) 分析了非线性渗流参数、窜流系数、弹性储容比和边界条件对试井曲线形态的影响规律.结果表明：基质的非线性渗流主要影响了裂缝与基质之间的物质交换.当大裂缝与小裂缝、大裂缝与基质之间的窜流能力相同时在压力导数曲线上只出现一个凹子，当两者不同时将出现两个凹子.微裂缝储容比的增加仅使第一个凹子的深度加大，而基质储容比的增加会同时加深两个凹子的深度.

致谢：本文得到河北师范大学科技类基金(L2017B21)的资助，在此表示感谢.