可控脉动风场下矩形断面复气动导纳特性研究
2022-09-03李威霖牛华伟华旭刚陈政清
李威霖,牛华伟,华旭刚,陈政清
(湖南大学风工程与桥梁工程湖南省重点实验室,湖南长沙 410082)
引 言
随着桥梁跨径增长至千米级和高耸建筑高度增至300 m 以上,由大气湍流产生的抖振荷载可能成为结构的控制性动力荷载。复气动导纳函数是精确计算抖振时域荷载的关键参数[1⁃2],是脉动来流与抖振力在幅值与相位上的传递函数。对于流线型断面,气动导纳可用Sears 函数进行表示,但对于钝体断面,由于其复杂的流动分离现象,其气动导纳理论表达式仍是风工程领域尚未解决的难题。
气动导纳现有研究主要依赖于风洞试验,根据来流特性不同可分为被动格栅产生的宽频脉动湍流下识别[3⁃4]和主动风洞产生的谐波来流下识别[5]。被动格栅虽能模拟大气边界层风场的部分湍流特性,但较难产生大尺度的低频漩涡[6],而模拟的小尺度高频漩涡又对钝体断面的流动分离影响很大。因此采用被动格栅风场识别的气动导纳结果常有一定的离散性[7],识别结果需要进行重复验证。
谐波脉动来流通常由多个振动机翼组成的主动格栅装置产生,也可在多风扇主动风洞内产生[8]。在该风场下识别的气动导纳重复性较好,便于工程应用,如薄机翼断面的气动导纳Sears 函数在正弦脉动流场下已被多名学者证实[9⁃11]。而对钝体断面,许多学者如Jancauskas 等[11]、Diana 等[12]、Ma 等[13]在主动风洞中识别了气动导纳,但仍有三个问题尚未得到有效解决:1)谐波风场参数如风攻角、谐波幅值对复气动导纳的影响;2)单频率和多频率组合谐波风场下识别的复气动导纳是否一致;3)结构运动状态对复气动导纳的影响。
上述第一个问题涉及到钝体断面的气动导纳是否与脉动风幅值有关,这需在不同幅值下的脉动风进行气动导纳识别;第二个问题本质为不同频率抖振力的可叠加性,Diana 等[12]通过主动风洞产生了多次谐波,验证了流线型箱梁的竖风向复气动导纳满足线性叠加性,但对钝体断面,升力与阻力气动导纳的可叠加性尚不清楚;第三个问题涉及到由脉动风引起的抖振力与结构运动引起自激力之间的可叠加性,Yan 等[14]发现在被动格栅湍流风场下结构运动状态严重影响气动导纳,但在谐波风场下气动导纳是否受结构运动状态影响尚不清楚。
由于需要复杂的机械装置且难以准确控制所产生的谐波参数[15],上述问题通过风洞试验较难解决,相比而言,CFD 数值模拟在气动导纳识别方面有着巨大的潜力,具有改变来流风场特性的简易性及流场可视性好等优点。如Rasmussen 等[16]、Hejlesen等[17]通过离散涡方法识别了湍流场下桥梁断面的气动导纳;唐煜等[9]、张伟峰等[10]、及Kavrakov 等[18]采用单频率谐波识别了一系列桥梁断面的气动导纳,但对涉及前述三个问题的研究鲜有报道。
鉴于此,本文基于2 维不可压URANS 方法,首先介绍了在CFD 中如何产生单频率、多频率组合的竖风向和顺风向脉动气流,并针对宽高比为4 的矩形断面,分别识别了其在不同风攻角、谐波幅值下的升力和阻力复气动导纳;然后识别了在多频率组合谐波风场下的气动导纳来验证抖振力的可叠加性;最后通过断面在竖向和扭转简谐运动下的复气动导纳研究抖振力与自激力的可叠加性。
1 气动导纳及谐波风场产生
1.1 气动导纳定义
根据Sears 气动导纳经典理论,当正弦脉动气流作用于桥梁断面时,需采用气动导纳来考虑抖振力的非定常特性,单位长度下的抖振升力和阻力系数可表示为:
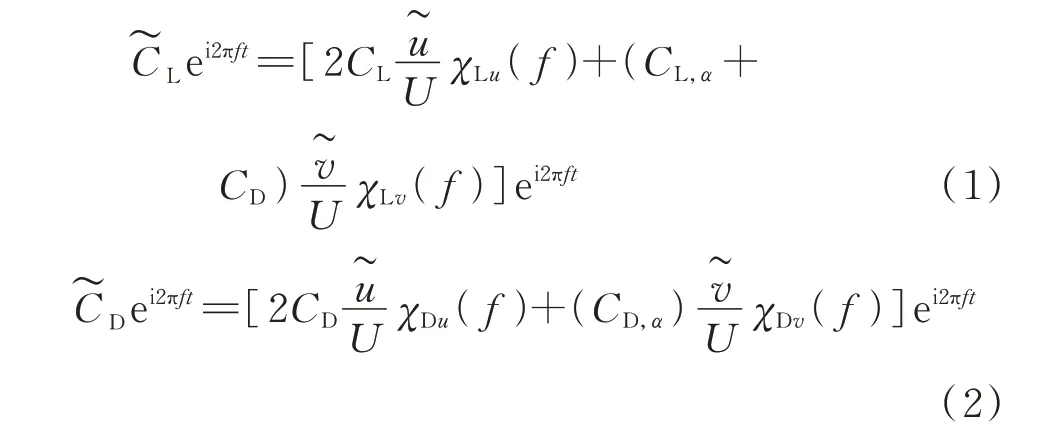
式中t为时间,f为脉动风频率,CL和CD分别为平均升力与阻力系数,CL,α和CD,α为升力和阻力系数的导数,和为顺风向和竖风向正弦气流的复振幅,χLu和χLv分别为顺风向和竖风向的升力复气动导纳,χDu和χDv分别为顺风向和竖风向的阻力复气动导纳。


为与经典理论对比,将竖向气动导纳与Sears 函数对比,计算相位时风速点选矩形截面的中点位置处[19];对顺风向气动导纳的模常与Davenport[20]公式对比,而其相位由于仍未有相关的理论表达式,仍采用Sears 函数的相位,风速点选矩形的迎风侧处,具体公式如下:
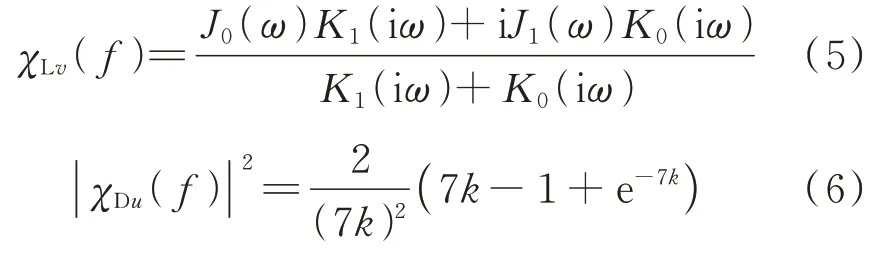
式中ω=πfB/U;J0,J1分别为第一类Bessel 函数,K0,K1为修正的第二类Bessel 函数;对阻力气动导纳,折减频率k=fD/U。
1.2 谐波脉动流场产生
由以上定义式可知,气动导纳的识别需先产生正弦竖向与顺风向脉动气流。对理想二维不可压缩流体,竖向和顺风向脉动风场的理论表达式为:

式中u,v分别为脉动风速的顺风向和竖风向分量;x为平均风速方向;U为平均风速;Au,Av为顺风向和竖风向的脉动风幅值。
上述脉动气流若想在计算域或风洞中实现,必须满足两个条件,第一为连续性欧拉方程,即:

将式(7)和(8)代入式(9)可知,对竖向脉动气流的表达式已满足欧拉方程,但对顺风向脉动气流却不能满足,从而在入口处会引起不可控的压力,进而影响数值计算结果。
第二个条件需考虑上下边界的影响,即在边界处脉动风速分量v必为0,可知式(7)不满足边界条件,这样会导致产生脉动气流幅值会随速度方向传输而折减,进而影响气动导纳的识别精度。
因此为保证所产生脉动气流满足上述两个条件,引入涡旋数n和余弦函数以修正上述脉动风公式:
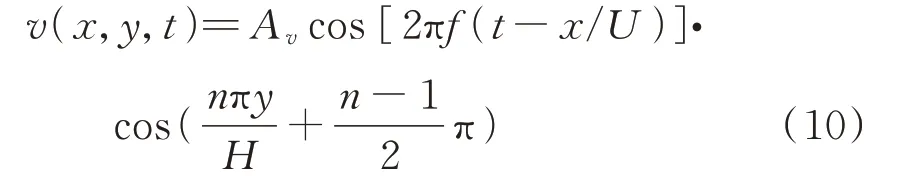
式中H为计算域高度,y为高度方向,将上述公式代入式(9)可得:
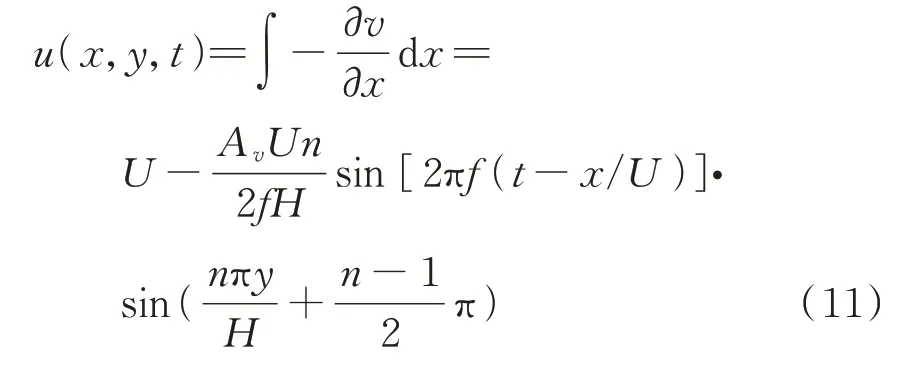
由式(10)和(11)可知:当涡旋数n=1 时,即可在计算域中部产生仅有竖风向谐波脉动风;当n=2时可产生顺风向谐波脉动风。由于CFD 改变参数的灵活性,计算中可以控制所产生脉动风的幅值、风攻角,也可产生多频率组合谐波以验证气动力的叠加性。
2 数值模型及验证
2.1 4∶1 矩形网格及数值模型设置
基于OPENFOAM 开源软件,将上述式(10)和(11)编程,并作用于计算域内入口以产生可控谐波风场。图1为宽高比B/D=4∶1 的矩形断面所采用的计算网格,整体尺寸为30B×20B,入口处采用速度入口,雷诺数为2×105,上部和下部采用对称边界。计算网格由4 个不同细化等级的矩形区域组成,靠近矩形断面处的网格尺寸最小,细化等级最高,具体如图2所示。
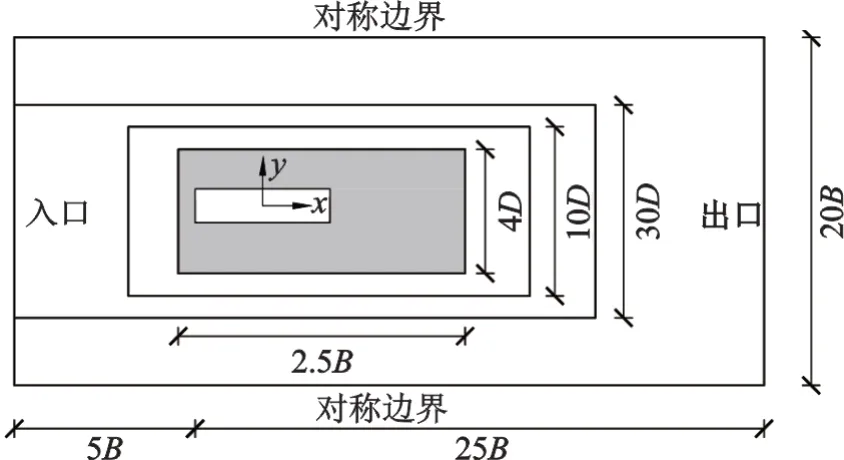
图1 4∶1 矩形计算域示意图(非真实比例)Fig.1 Overview of 4∶1 rectangular section in CFD(the figure does not respect real proportions)

图2 近壁面网格尺寸图Fig.2 Detailed meshes around solid boundary
离散方程组求解采用瞬态PISO 算法,湍流模型为k‑ωSST,该设置广泛应用于二维桥梁断面三分力系数、颤振导数等气动参数的识别。图1的灰色区域可为动网格,使矩形做竖向或扭转正弦运动,以研究运动状态对气动导纳的影响。由于复气动导纳的识别为单一频率法,需涉及多工况,因此所有计算均在湖南大学国家超级计算中心进行。
2.2 网格独立性验证及三分力系数
为验证上述数值模拟设置的正确性,首先进行了网格独立性验证,网格参数如表1所示,共采用了粗、中、细三种网格,y1为边界层网格第一层高度,随着网格细分逐渐降低,而边界层数逐渐增大。Y+的平均值从7.69 到1.58 变化,网格总数量为5.5 万到14 万。
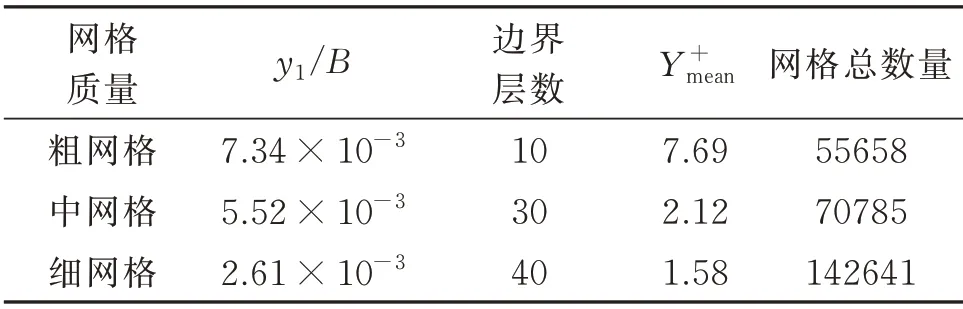
表1 不同网格的主要参数Tab.1 Main parameters for different meshes
图3为4∶1 矩形断面在均匀流下不同网格的压力系数统计值分布,并与文献[21]的风洞试验对比,可知具有较好的网格独立性,而且与试验值吻合较好,证明了此数值模拟设置的正确性。为兼顾计算效率和准确性,以下运算均采用中等网格。

图3 均匀流下不同网格压力系数的统计值分布Fig.3 Distribution of statistical pressure coefficients for different meshes in uniform flow
图4为±6°攻角范围内4∶1 矩形断面的阻力与升力系数,并分别与文献[22⁃23]的CFD 和风洞试验结果对比可知,虽然风攻角增大存在一定的偏差,但在可接受范围内。
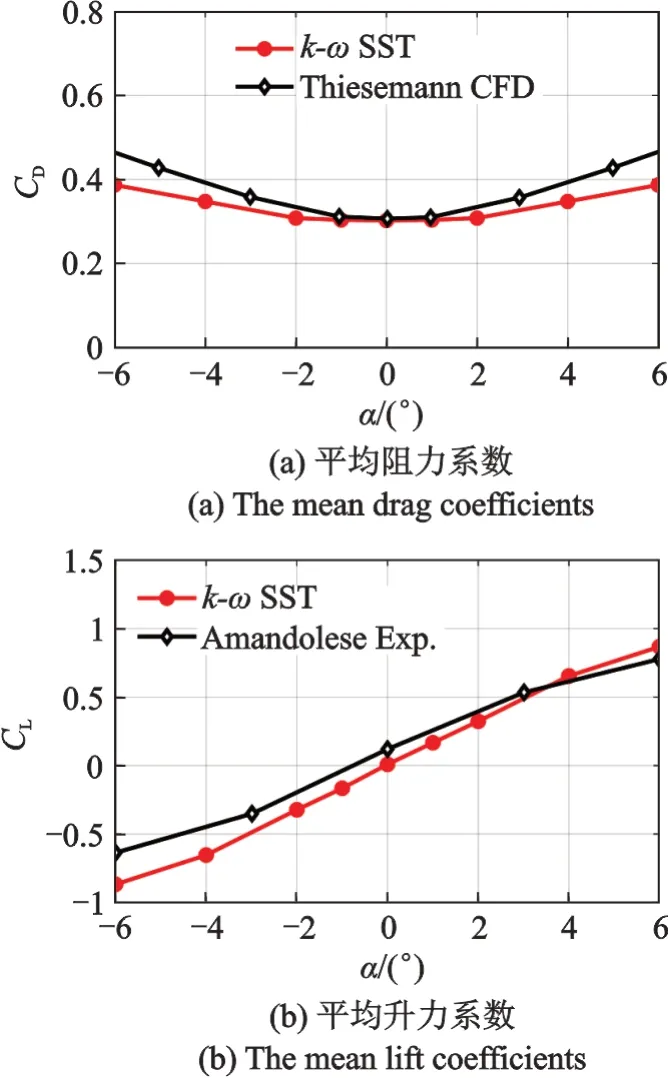
图4 平均阻力系数与升力系数随风攻角变化Fig.4 Drag and lift coefficients change as wind attack angles
2.3 谐波脉动流场
为检查谐波来流效果,首先在空风场下图1中的坐标原点处测试了风速时程曲线。图5左侧分别给出了顺风向、竖风向单频率及竖风向5 阶频率组合谐波的时程、FFT 曲线。可知CFD 流场内产生的谐波与公式(10)和(11)的输入值在幅值和相位均符合较好;同时右侧也给出了相应最后时间步下的流场图,可知对竖向谐波流场涡旋数n=1,而顺风向流场涡旋数n=2,验证了上述理论公式(10)和(11)的正确性,也表明本文提出的方法能在CFD 中产生符合N⁃S 方程及边界条件的可控脉动气流。

图5 坐标(x,y)=(0,0)处不同谐波风场的风速时程、FFT 曲线及对应的流场图Fig.5 Time history and FFT of harmonic fields at the measured point(x,y)=(0,0)and the corresponding wind fields
3 气动导纳识别结果
基于前述模拟风场,首先研究风攻角、谐波幅值对竖风向与顺风向复气动导纳的影响,然后通过作用多频率谐波识别的气动导纳来验证抖振力的线性叠加性,最后让矩形断面做竖向及扭转简谐运动来验证抖振力与自激力的可叠加性。复气动导纳的识别由式(3)和(4)得到,其中抖振力的幅值和相位采用正弦函数拟合其时程曲线得到,较容易消除涡激力及高阶分量的干扰。为保证识别精度、减少初始流场影响,每个单频率下的模拟都保证至少有12 个周期的正弦波,而仅有最后8 个周期的正弦波用于计算气动导纳。
3.1 风攻角
由于4∶1 矩形为对称截面,以下仅给出气动导纳在风攻角为0°,+1°,+3°下的识别结果,其中竖向单频率谐波幅值Av/U均为0.0175,从而脉动风引起的最大风攻角为1°,对顺风向气动导纳识别时,谐波幅值Au/U为0.05。
图6为升力复气动导纳的绝对值与相位在不同风攻角下的识别结果,识别的折减频率区间fB/U为0~0.4,可发现在0°和+1°风攻角时绝对值与文献[11]的实验值吻合较好,表现为在低频处大于Sears函数,并且数值保持为单位1,符合准定常准则,而后随折减频率增大而减少;当风攻角增大到+3°,气动导纳与Sears 接近;升力气动导纳的相位在不同攻角下均与Sears 函数显著不同,表现为随折减频率增大而逐渐降低,当风攻角增大到+3°时,在折减频率为0.1 时发生了较大变化。

图6 升力复气动导纳随风攻角的变化Fig.6 The lift AAF change as wind attack angles
图7为不同风攻角下的阻力复气动导纳的绝对值和相位变化,折减频率区间fD/U为0~0.1,可以发现阻力气动导纳的模在低频处接近1,但在高频处显著低于Davenport 值,这与Kavrakov 识别箱梁断面的结论很类似[18]。当攻角增大至+3°,与升力气动导纳类似,气动导纳值开始出现了偏差。阻力气动导纳的相位随折减频率先升后降,随攻角增大也出现一定偏差。
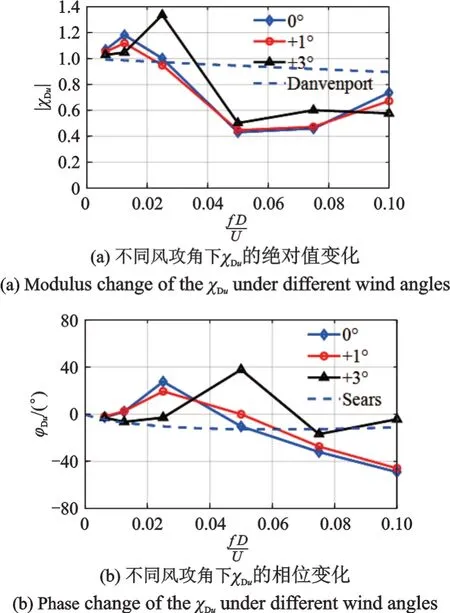
图7 阻力复气动导纳随风攻角的变化Fig.7 The drag AAF change as wind attack angles
为探究较大风攻角引起升力与阻力气动导纳变化的原因,可参见如图8所示的平均流线图。在1°风攻角时,矩形顶部的负压区气泡先分离然后会发生再附着,但当风攻角增大至4°时,气泡分离后不再附着,矩形后缘处的尾涡也发生显著改变,从而引起了气动特性的改变,这与Patruno 对5∶1 矩形截面的研究结论一致[24]。
3.2 脉动风幅值
为研究单频率下谐波幅值对矩形气动导纳的影响,针对0°平均风攻角,识别了6 种不同幅值下的升力及阻力复气动导纳。如表2所示,其中前3 个工况为仅有竖向脉动风作用,引起的最大瞬时风攻角为1°~4°,后3 个工况为仅有顺风向脉动风,幅值为(0.05~0.15)U。

表2 单频率下不同谐波幅值工况Tab.2 Amplitude of the input harmonic
图9为升力复气动导纳随不同竖向谐波幅值的变化。当Av/U<0.035,即竖向脉动风引起的最大风攻角在2°以内时,升力气动导纳的模和相位基本保持不变;当Av/U增大至0.07,最大风攻角为4°时,气动导纳的模有一定偏离。对气动导纳的相位,不同的脉动风幅值对其影响较小。这表明,对矩形断面的升力气动导纳应考虑脉动风幅值的影响,引起这种现象的原因也可由图8解释,当风攻角在±4°范围内变化时,分离气泡在附着与不再附着之间变化,导致气动导纳随脉动幅值变化。
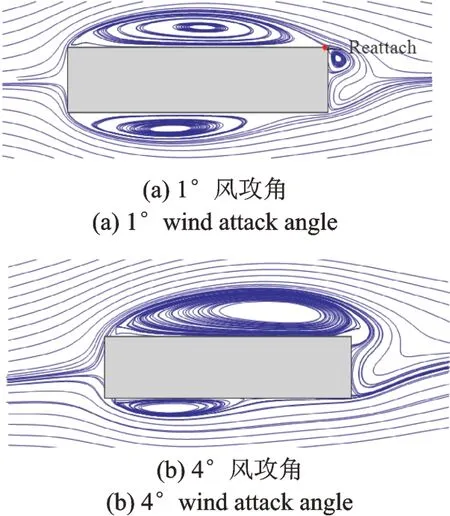
图8 不同风攻角下平均风速流线图Fig.8 Streamlines in different wind attack angles
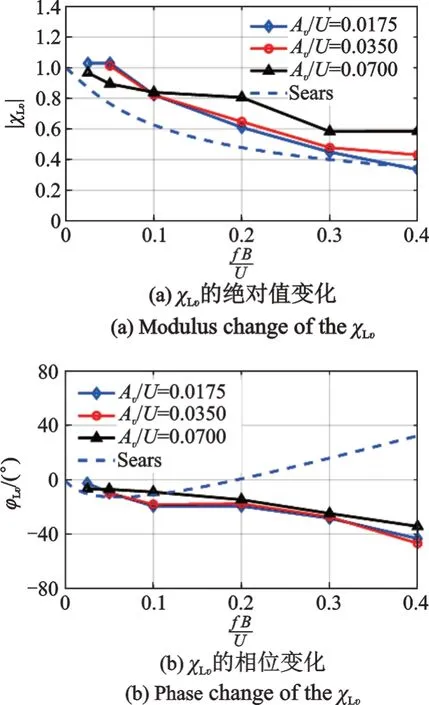
图9 升力复气动导纳随竖向谐波幅值变化Fig.9 The lift AAF change as vertical harmonic amplitudes
图10 为阻力复气动导纳随顺风向谐波幅值的变化曲线,顺风向谐波幅值对阻力气动导纳的模和相位在低频处影响较小,但在折减频率大于0.05后,增大幅值会引起阻力气动导纳的模增大,对其相位也有一定影响。
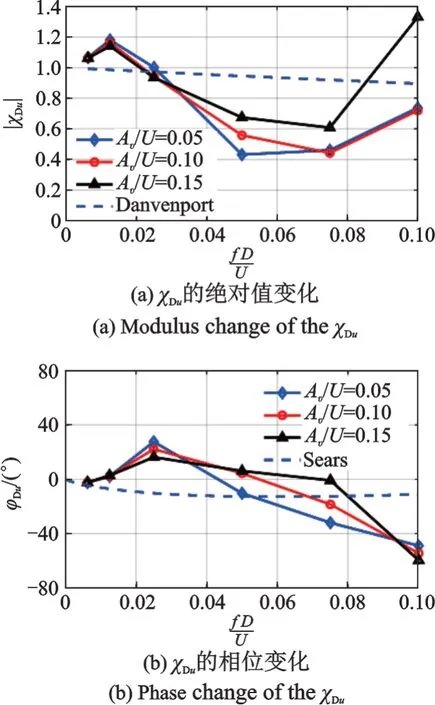
图10 阻力复气动导纳随顺风向谐波幅值变化Fig.10 The drag AAF change as along⁃wind harmonic am⁃plitudes
3.3 多频率组合谐波
通过产生多频率组合的竖向和顺风向谐波风场,验证4∶1 矩形断面的抖振力叠加性。如表3所示,前3 个工况为仅有竖风向的包含2,3,5 阶频率的谐波,对顺风向验证了3 阶频率谐波,为避免谐波幅值的影响,设置多频率组合谐波下的幅值与单谐波幅值保持一致。
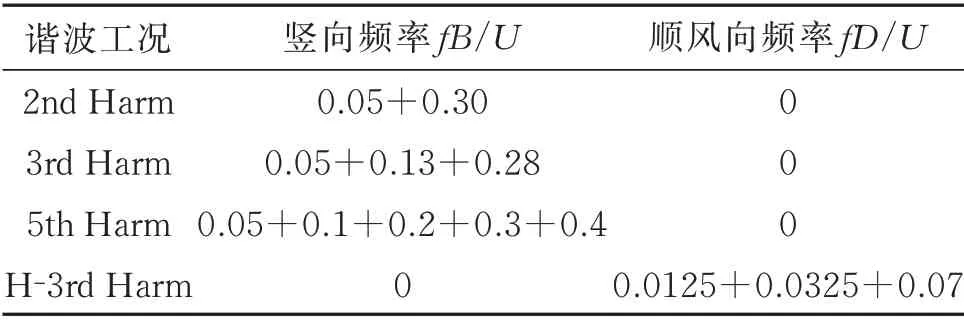
表3 多频率组合谐波工况Tab.3 Multi‑frequency harmonic fields
图11 为不同组合谐波下的抖振升力的傅里叶变换曲线。为方便对比,单谐波工况仅给出折减频率为0.05 时的结果,可发现在该频率处不同谐波工况的抖振升力幅值基本一致,2 阶谐波与5 阶谐波在折减频率0.3 处幅值也基本一致。
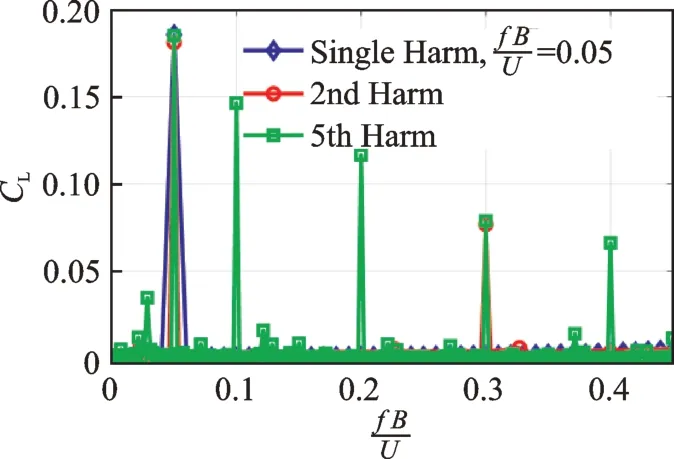
图11 不同组合谐波下抖振升力的FFT 曲线Fig.11 The FFT of buffeting lift coefficient under different vertical harmonics
图12 给出了上述多频率组合竖向谐波下升力气动导纳结果。可知,在2,3 及5 阶谐波作用下,该矩形断面的升力气动导纳在幅值和相位上均具有很好的叠加性,验证了在谐波脉动风场下,不同频率的抖振升力具有很好的线性叠加性,这与Diana 等[12]对Humber 桥升力气动导纳的结论一致。
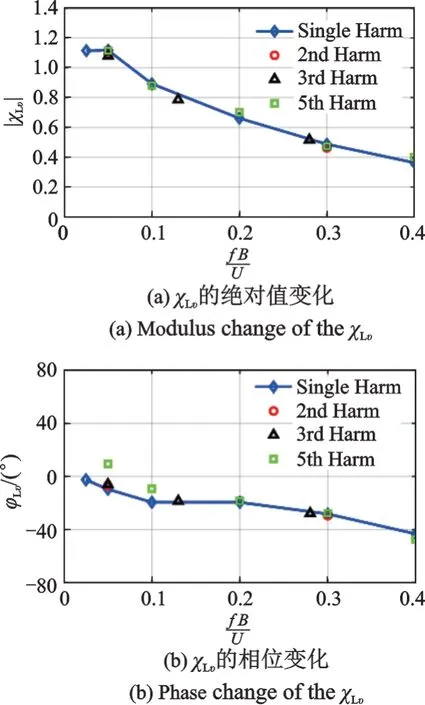
图12 竖向组合谐波下的升力复气动导纳Fig.12 The lift AAF in different vertical multi⁃frequency harmonics
图13 为顺风向3 阶谐波组合作用下的阻力复气动导纳结果。可知3 阶谐波与单谐波下结果基本一致,表明该断面的抖振阻力在幅值和相位上也具有很好的叠加性。

图13 顺风向组合谐波下的阻力复气动导纳Fig.13 ThedragAAFindifferentalong⁃wind multi⁃frequency harmonics
3.4 运动状态
自激力由结构的运动产生,而由脉动风引起的抖振力与自激力之间的可叠加性尚未得到验证,这也是广泛应用于桥梁颤抖振分析的理论基础。大跨桥梁抗风设计关心的折减频率常在0~1 之间,因此选取竖向和扭转简谐运动的折减频率fB/U=0.25,由于断面运动和输入谐波的频率不同,抖振力和自激力能很精确分离。为避免结构运动引起的瞬时风攻角过大而引起气动力的非线性,控制竖向和扭转的运动幅度,以保证由断面运动引起的最大风攻角在±1°以内变化[25]。
图14 为升力复气动导纳的模和相位随不同运动状态的变化曲线,可发现竖向和扭转简谐运动对升力复气动导纳影响不大,除在折减频率为0.2 时有一定偏差外,其他基本一致。这表明在此运动状态下,将该断面的抖振升力与自激力分开处理在谐波风场下是可行的。
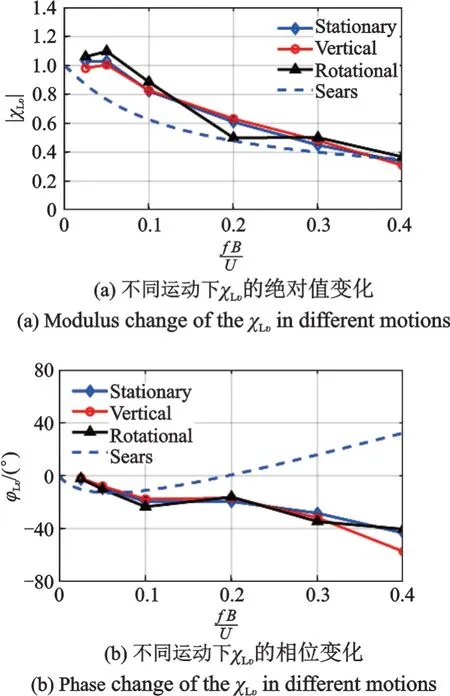
图14 运动状态对升力复气动导纳的影响Fig.14 The lift AAF change as different motions
图15 为阻力复气动导纳随不同运动状态的变化,可知竖向简谐运动对阻力气动导纳影响较小;但当断面做扭转简谐运动时,阻力气动导纳在高频处增大,且接近Davenport 理论值。这表明在谐波风场下,由高频脉动风引起的抖振阻力受扭转运动的影响较大。

图15 运动状态对阻力复气动导纳的影响Fig.15 The drag AAF change as different motions
4 结 论
基于2⁃D URANS,研究了4∶1 矩形断面在不同谐波脉动气流参数及结构运动状态下的顺风向和竖风向复气动导纳函数,根据数值计算结果可得出以下结论:
(1)提出的模拟方法能有效在CFD 内产生幅值可控的竖向和顺风向谐波脉动风场,测试值与目标值基本一致。
(2)在0°风攻角下,识别的4∶1 矩形断面升力复气动导纳与风洞试验值吻合好,表明该数值方法可应用于钝体断面复气动导纳的识别;较大的风攻角和谐波幅值均会对复气动导纳产生影响,根本的原因是过大的瞬时风攻角使气流在矩形顶部发生分离后不再附着,从而引起气动特性的改变。
(3)在多频率组合和单频率谐波风场下识别的升力与阻力气动导纳基本一致,验证了不同频率的抖振力具有较好的可叠加性。
(4)当竖向和扭转简谐运动引起的风攻角在±1°时,升力气动导纳与断面静止时基本一致,在颤抖振分析中将该断面的抖振升力与自激力分开处理在谐波风场下是可行的。
(5)当简谐运动引起的风攻角在±1°范围内,竖向简谐运动对阻力复气动导纳影响不大,但当折减频率fD/U>0.04 后,扭转简谐运动会增大阻力气动导纳的绝对值。
