关于Arrhenius公式的几点讨论

张晨曦，苏涵，张树永

山东大学化学与化工学院，济南 250100

Arrhenius公式于1889年由实验结果得出，是最重要的化学动力学经验公式，是支撑化学动力学理论发展的两大实验基础之一，其所建立的活化能概念更是影响深远。但一百多年来，对该公式的讨论从未停止，主要集中在以下几个方面：(1) 能否从热力学公式(如van’t Hoff方程)导出Arrhenius公式？(2) 活化能的定义及物理意义到底是什么？(3) Arrhenius公式适用的温度范围及其修正；(4) Arrhenius公式和与之形式类似的公式(如van’t Hoff方程等)是否存在内在联系？

本文追溯了Arrhenius公式产生的历史过程，指出了当前讨论中存在的一些问题，提出了改进的意见和建议。这些讨论有利于纠正一些错误认识，使读者正确理解和应用Arrhenius公式。

1 Arrhenius公式的提出

1884年，van’t Hoff首先得到速率公式(1)，并延伸得到公式(2)[1]：

其中，T为绝对温度，k为速率常数，q为在恒定体积下过程的热效应，A、B为经验常数。van’t Hoff从反应分子数出发，研究了多个单分子及多分子反应，得到了k与T的经验关系，并发现这些经验关系存在较大差异，在其整理的8个反应的k-T关系中，只有氯乙酸水溶液的分解反应在80-130 °C的温度范围内具有与后来的Arrhenius公式相似的形式。故van’t Hoff指出“我将不强调经验和经验结果的一致性，而强调从目前的经验中可以得出的一般结论，即：温度对转化速度的影响随所考虑的反应而变化。”van’t Hoff选择尊重实验事实，他的结论是：针对不同的反应，式(2)中的常数A可以为零，而B可以不为零。他没有明确常数A、B的物理意义，并认为该式不具有普遍适用性[2]。

1889年Arrhenius得出速率r和温度T的关系式为：

其中A是常数，T0、T1是绝对温度，是不同温度下的反应速率。他给出了7个实验的数据，证明了上述公式成立。结合van’t Hoff速率方程(式2)，他引入假设，以蔗糖水解反应为例，指出反应速率和“活性蔗糖”的量成比例，且在恒温下可以近似认为“活性蔗糖”的量与“非活性蔗糖”的量成比例。此时有：

这两个公式后来都被称为Arrhenius公式，式(4)是其微分形式，式(5)是其积分形式。Arrhenius赋予q活化能的概念，并给出了活化能的物理意义：反应物分子转变为活化分子所需的能量。显然，相较于van’t Hoff最初提出的动力学公式，Arrhenius舍去了常数B，并赋予了van’t Hoff速率公式A以明确的物理意义，使该公式具有了普遍使用的合理性[3]。

追溯历史，Arrhenius是基于实验事实得出公式(4)和(5)的，并非从van’t Hoff方程导出或类比得到的。而van’t Hoff则是先得出类似Arrhenius公式的动力学方程(式2)，进而导出了热力学关系。现在一直有人试图从热力学的van’t Hoff方程导出动力学的Arrhenius公式。不难发现，在该推导过程中，出现了“想当然”的对应关系，即将活化能Ea与反应物或者生成物的标准摩尔生成吉布斯自由能之和对应[4]：

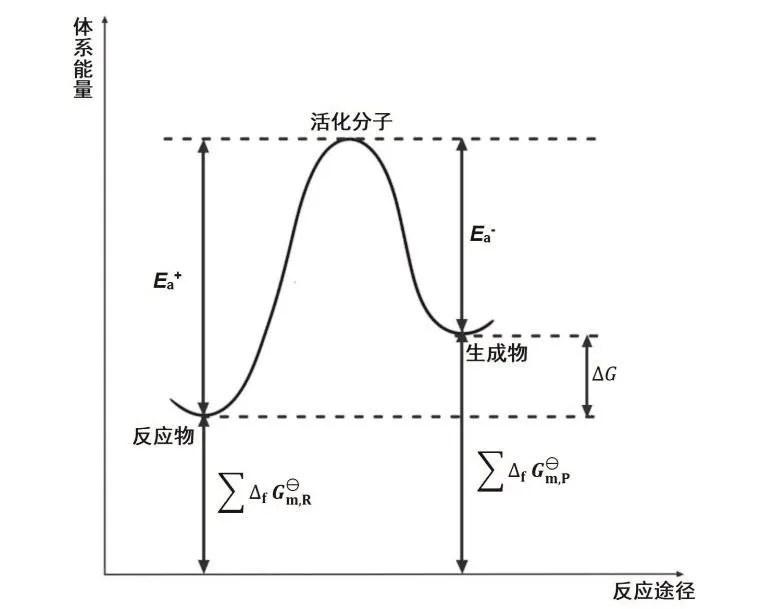
图1 标准状态下化学反应体系自由能变化与体系状态的关系图

从哲学角度而言，运动是绝对的，静止是相对的，van’t Hoff方程所对应的平衡状态，实际上是一个特殊的运动状态(正逆反应速率相等)，故从动力学速率相等导出热力学平衡关系是可行的，反之则不然。

2 活化能的物理含义

1996年，IUPAC推荐的活化能定义是Arrhenius图(lnk-1/T图)中直(曲)线在温度T下的斜率[5]。该值来源于实验，故称实验活化能(experimental activation energy)。与具有明确定义和物理意义的其他物理量不同，反应的活化能存在多种解释。不考虑简单碰撞理论、过渡态理论和光化学等对活化能的不同理解，人们给出的活化能定义主要有以下三种[6]：

(1) Arrhenius (1889)：反应物分子转变为活化分子所需的能量。

(2) Lewis (1918)：活化分子能量的最低值与反应物分子平均能量之差。

(3) Tolman (1925)：活化分子平均能量与反应物分子平均能量之差。

Arrhenius指出，只有能量足够高的分子才能发生反应，而达到反应所需能量的分子称为活化分子。对于单分子反应而言，活化分子的概念容易理解，但对于多分子反应却存在歧义。以A + B → C反应为例，是A、B分子都必须达到活化状态才能发生反应？还是A分子和B分子整体达到反应所需的能量就能发生反应？如果是后者，则发生反应的A、B分子不需要都成为活化分子，此时的活化分子和活化能的物理意义不再明确。

从目前普遍接受的Tolman定义来看，Tolman首先从单分子基元反应出发，基于简单碰撞理论，在宏观非快速、服从Boltzmann分布的气相或稀溶液条件下，结合化学动力学和统计力学导出：

对于双分子反应而言，Tolman提出了两种机制，其一是A、B两种分子均达到活化状态然后碰撞发生反应，即将活化和反应分开；其二是未被活化的A、B分子碰撞的能量超过了平均动量直接反应，此时活化和反应过程融合[7]。两种机制下的Ea具有截然不同的物理意义。第一种情况下：

即双分子反应活化能为两种活化分子的平均能量与所有分子的平均能量之差，满足式(8)的定义，但不符合简单碰撞理论模型。在简单碰撞理论中，只要分子碰撞的相对平动能在质心连心线上的分量超过某一阈值即可反应，并不要求两种分子都达到活化状态。

在第二种情况下，每个分子都活化不是反应的绝对前提，只要A、B两种分子的碰撞速率达到某一临界值或者整体动量达到某一阈值，即可直接反应。这种机制满足简单碰撞理论模型也相对合理，但不再符合Tolman对活化能物理意义的解释。在此，我们借鉴溶液化学“遭遇对(encounter pair)”的概念，引入“活化分子对(activated molecule pair)”或者“反应分子对(reactive molecule pair)”概念，指代可以发生反应的一对或者一组分子。根据统计热力学原理，假设“活化分子对”的数量比例依然满足Boltzmann分布，则类比单分子反应活化能的物理意义，可以得出多分子反应活化能的表达式为：

因此，我们建议拓展Tolman定义中的“活化分子”概念，将活化能定义为：活化分子或活化对的平均能量与反应物分子或反应物分子对平均能量之差。其中，活化分子对应单分子反应，活化对对应多分子反应。需要说明的是，修改后的定义虽然更加合理也更加符合实际，但由于活化对中每个分子的能量并不确定，故无法使用Boltzmann分布说明其各自所占的比例。

3 Arrhenius公式的温度适用范围

作为最基本的动力学公式，Arrhenius公式应用领域虽然广泛，但仅适用于五类k-T关系中的第一类和第五类，对第二到第四类并不适用[8]。但即使是第一类和第五类反应，其使用的温度范围也是有限的。随着实验技术的发展以及应用领域的拓展，人们发现Arrhenius公式的lnk与1/T的线性关系只在某个温度范围内能够保持，一旦超出该温度范围，则线性变差，此时需要对Arrhenius公式进行修正。

1955年Hyne和Robertson结合Everett和Wynne-Jones提出的平衡常数与温度的三常数公式[9]提出了动力学三常数Arrhenius修正公式：

A、B、C都是与温度无关的常数[10]。早在1893年Kooij曾提出相似形式的公式[11]，因不够简洁、物理意义不明确而未普遍使用。随着动力学的发展，该修正公式各参数被赋予了明确的物理意义，并变为以下形式：

其中，A和Ee都是与温度无关的常数，m为实数[12]。经过校正后，Arrhenius公式的适用温度范围可以大幅度提升。

目前，虽然多数教材都强调了二常数Arrhenius公式应用的温度限制，却并未明确指出公式适用的温度范围。在此，我们基于式(12)，通过定量计算说明Arrhenius公式对常见反应的适用温度范围。

对式(12)取对数后微分

可以证明，此时反应的活化能符合：

与式(2)比较可知，式(2)中的常数A与能量项(Ee)有关，而B则与活化能随温度的变化程度m有关。如果m = 0，则lnk与1/T在任何温度范围内都符合线性。但实际上，几乎没有反应的lnk与1/T的关系能够在如此广泛的温度范围内保持线性，这说明m通常并不为零。随着温度的升高，mRT的影响逐步加大，导致温度对活化能的影响不能再被忽略时，即会导致lnk与1/T的关系偏离直线。需要说明的是，对于预测电子材料使用寿命等对温度要求比较严苛的精密技术领域，这种微小偏差也可能导致比较严重的问题。

化学反应的活化能通常在40-400 kJ·mol−1，活化能小于80 kJ·mol−1的为快反应，活化能超过120 kJ·mol−1为慢反应，这两类反应通常很难研究，故人们研究的常见反应的活化能通常在80-120 kJ·mol−1的范围内。为了直观地体现m和T的变化对活化能的影响，我们取Ee为80 kJ·mol−1，m= 0-10，T= 273.15-1073.15 K，将三常数公式(式13)计算值看作真实值，分别利用三常数公式(式13)和二常数公式(式15)作图所得斜率分别求出对应的活化能示于图2。

图2 Ea (三常数)和Ea (二常数)与1/T和m的三维关系图

二常数公式：

图2是首次报道，可用于判断二常数Arrhenius公式在不同m和T下的温度适用范围。

其显示，当温度较低、m值较小时，使用三常数和二常数公式所得的Ea是重叠的。通常，在温度变化不大、分子结构比较简单、不考虑振动影响时，m通常不大于4[13]。如果取m= 0.5，则在室温(293.15 K)下，mRT的数值只有1.22 kJ·mol−1，只占正常活化能的1.0%左右，可以忽略其影响。这是Arrhenius公式能够成为普适性公式的前提。

在实验测量活化能时，人们通常从比室温略高的温度(如298.15 K)开始，以10 °C为间隔，在25、35、45、55、65 °C测量5个以上的点，前后的温差有40 °C。如果实验的温度测量精度可以达到0.1-0.01 °C，温度测量的相对误差在±(0.1%-1%)，则对于Ee为80 kJ·mol−1的反应，在上述温差范围内活化能改变±1%所对应的m值为6.0 (见表1)。

表1 Arrhenius曲线图相关数据

由表1可以看出，活化能改变−1%时，线性相关系数依然很好，这说明线性并不能用于判断Arrhenius公式是否适用。

图2显示，随着温度的升高和m值的增加，依据二常数和三常数公式所得活化能出现明显的差异。这说明，对于复杂分子、超过40 °C的温差或者对活化能测量要求较高时，应采用三常数公式进行拟合。

4 公式形式相似的必然性

在物理化学教学过程中，人们发现van’t Hoff公式等多个热力学公式具有与Arrhenius公式相似的形式，但参数的物理意义和使用条件却截然不同。之前已有不少作者对该现象进行了归纳和分析，但一方面归纳不全面，另一方面没有对出现相似性的本质给出解释。在此，我们总结了物理化学教材最常出现的与Arrhenius公式形式相似的公式(见表2)，并对导致其相似性的本质特征进行了说明。

从表2不难发现，这些形式相似的公式所描述的都是对峙的化学或物理过程达到平衡的状态。故一般的规律可以概括为：只要一个过程存在正向和逆向两个相反过程，且其正逆过程的变化速率均符合质量作用定律，且平衡时满足平衡常数等于正逆向过程的速率常数之比，即K=k+/k−，则描述该平衡状态性质的热力学公式一定具有与Arrhenius公式相似的形式。

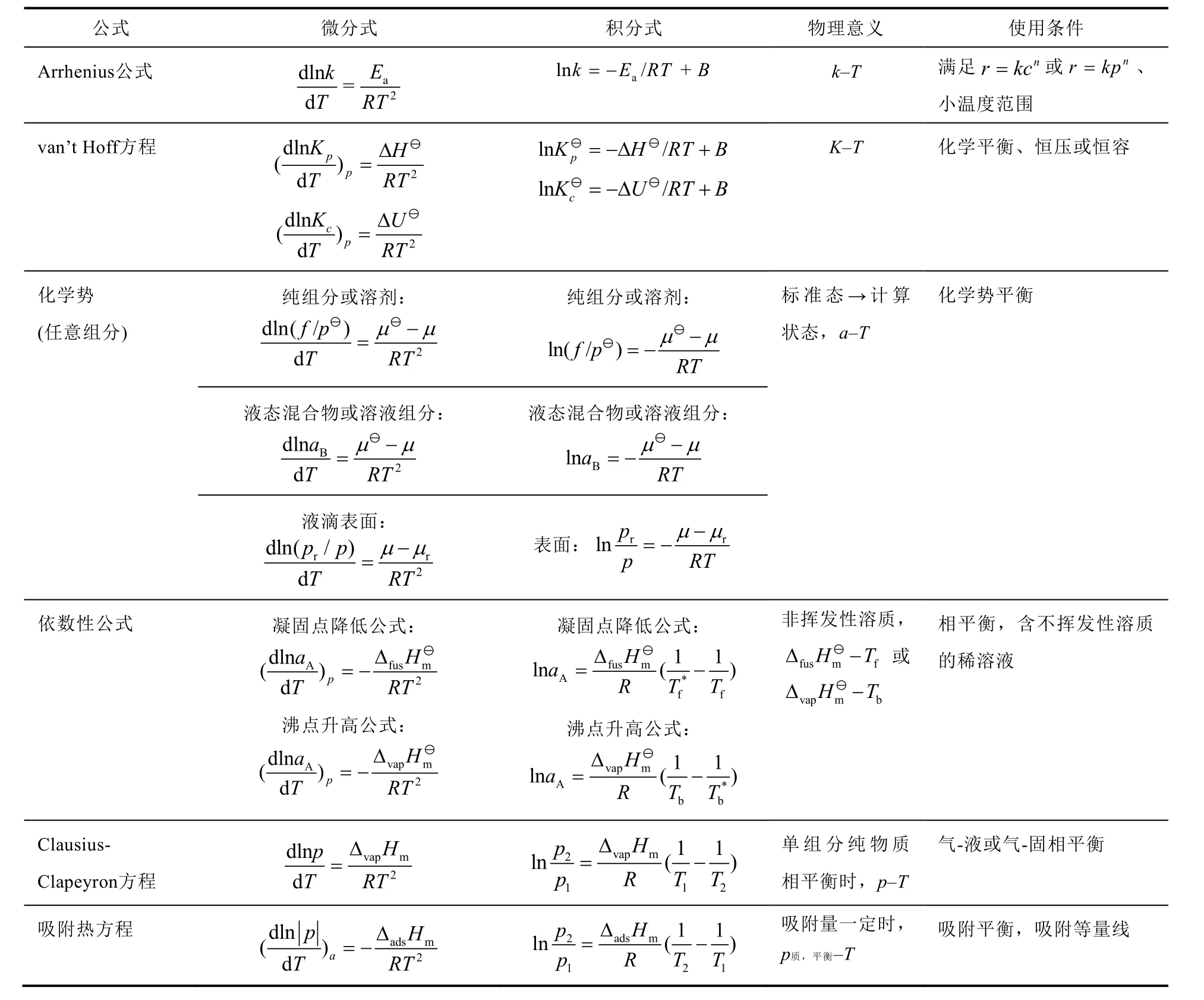
表2 Arrhenius公式及形式相似的热力学公式汇总

5 结语

从历史事实看，认为Arrhenius公式是由热力学的van’t Hoff方程类比而来的说法并不科学。从热力学出发证明Arrhenius公式无论是从物理意义上还是从哲学角度都不科学。Tolman活化能定义适用于单分子反应，对多分子反应最好引入“分子对”和“活化对”的概念进行修正。首次绘制了Ea-(1/T)-m关系曲面，清晰展示了在较宽的温度范围和较广的m取值下，三常数和二常数Arrhenius公式拟合所得活化能的差异。建议在大学物理化学课程及实验教学中应广泛介绍和使用三常数公式Arrhenius公式。明确了物理化学教材中诸多热力学公式与Arrhenius公式具有相似形式的本质是其所描述的状态均为达到平衡的对峙过程。