电弧铣削加工间隙电压预测模型的建立与研究

张 瑾 韩福柱

1.清华大学机械工程系，北京，1000842.清华大学精密/超精密制造装备和控制北京市重点实验室，北京，100084

0 引言

电弧铣削加工利用电弧放电产生的高温去除工件材料，其加工原理与电火花加工类似，但是加工过程中放电能量密度高，加工效率高，近年来广泛应用于钛合金、高温合金等难切削加工材料的加工。目前对于电弧铣削加工技术的研究主要集中在提出新的电弧铣削加工方法，研究新型加工电源，引入超声、磁场等辅助加工方式，以提高电弧铣削加工的效率[1-4]，而对电弧铣削加工间隙控制的研究尚属空白。目前电火花加工间隙的控制已经有比较完善的研究成果，如检测电火花加工间隙的平均电压[5]、建立放电加工模型[6-7]，以及提出不同的电火花加工状态预测方法等[8-9]，通过以上方法可识别电火花放电状态，检测电火花加工放电间隙，从而调整控制系统，实现稳定的电火花加工。在电弧铣削加工方面，对电弧加工间隙进行控制是非常有必要的，电弧铣削加工间隙的变化直接影响电弧铣削加工的效率。由于电弧铣削加工过程中放电能量密度高，工件表面材料在短时间内被大量蚀除，因而加工间隙的变化非常大，如果不对加工间隙进行控制，会影响电弧铣削加工时的放电频率，进而影响加工效率，因此，需要通过伺服系统控制加工间隙来保证电弧铣削加工的高效、稳定进行。

电火花加工过程中一般存在五种放电状态，分别是空载、火花、电弧、过渡电弧以及短路，而电弧铣削加工过程中，通常认为只有空载、电弧和短路三种状态，目前已有的电火花加工状态的预测模型是基于电火花五种放电状态建立的，无法用于电弧铣削加工的间隙控制。要实现对电弧铣削加工间隙的实时准确控制，就需要建立一种能够预测电弧铣削加工间隙的预测模型，通过该模型预测的加工间隙的变化来实现伺服系统对加工间隙的控制，从而提高电弧铣削加工的效率。本文根据系统辨识理论建立了电弧铣削加工系统的预测模型，通过实验验证了预测模型的准确性。

1 电弧铣削加工系统时域模型

电弧铣削加工过程中，放电间隙的大小受多种因素的影响，包括加工电压、电极转速、冲液压力、铣削深度、磁场强度、进给速度，以及电极和工件的材料、硬度等。理论上，当加工参数确定后，加工电压、电极转速、冲液压力、铣削深度、磁场强度及进给速度等加工参数在加工过程中就不会发生改变，可以认为加工参数是确定性的影响因素。在实际加工中，随着放电加工过程的进行，铣削深度和电极损耗的增加，会造成放电间隙变化、排屑情况变差等，这些外部因素对电弧铣削加工的影响会变大，可以认为这部分因素是不确定性的影响因素。因此，在电弧铣削加工系统中，系统应该包括确定性的部分、不确定性的(即干扰)部分影响因素，系统的示意图见图1。其中，y(t)是随时间变化的间隙电压值，u(t)是稳态加工时的初始加工间隙电压，e(t)是均值为0、方差为σ2的白噪声。

图1 电弧铣削加工系统示意图Fig.1 Schematic diagram of composite energy fieldrotating arc milling processing system

系统的输出响应可表示为

(1)

类似地，系统的噪声响应可表示为

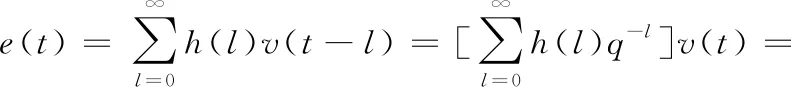
(2)

其中，G(z-1)称作系统脉冲传递函数，即系统模型；H(z-1)称作噪声脉冲传递函数，即噪声模型；q-1是移位算子，定义式为

q-1y(t)=y(t-1)

(3)

结合式(1)和式(2)，电弧铣削加工系统的时域模型可以表示为

z(t)=G(q-1)u(t)+e(t)=G(q-1)u(t)+
H(q-1)v(t)

(4)

式中，u(t)、z(t)分别为系统输入变量和输出变量；v(t)为均值为0、方差为σ2的不相关随机噪声。

(5)

(a)输入时域图

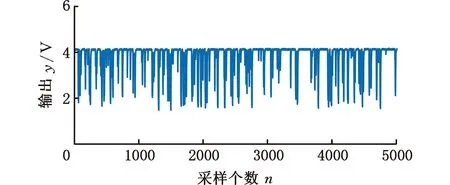
(b)输出时域图图2 输入输出时域分布Fig.2 Input and output time domain distribution plot

2 模型输入信号的预处理

对采样得到的数据进行谱密度分析，对应的频谱函数的估计如下：

(6)

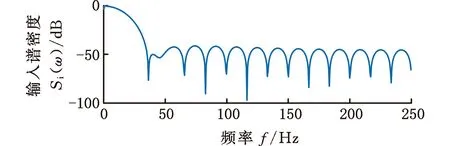
(a)输入谱密度

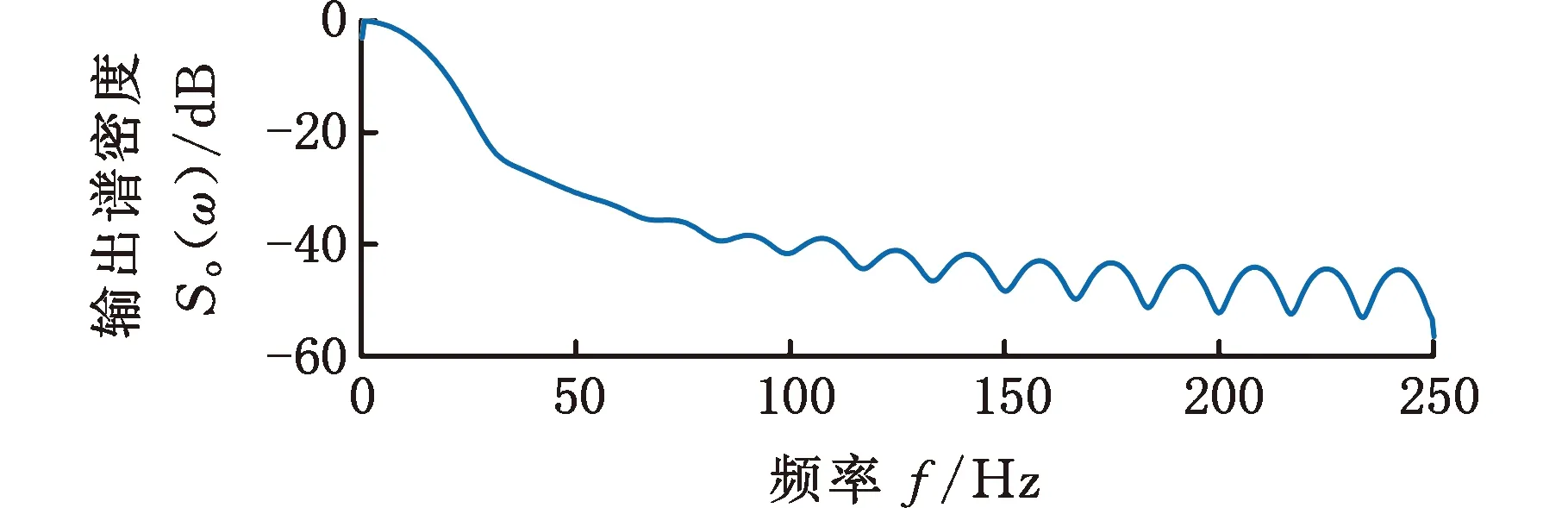
(b)输出谱密度图3 输入输出谱密度Fig.3 Input and output spectral density plot

其中，WM(τ)为窗函数，M为窗函数的宽度，本文采用Hamming窗(M=30)，由此得到电弧铣削加工系统模型的输入、输出谱密度函数，如图3所示。由系统的频率响应函数估计和噪声的频谱函数估计：

(7)

(8)

得到系统的频率响应函数波特图和干扰的频谱分布图，如图4和图5所示。

(a)幅值

(b)相位图4 传递函数波特图Fig.4 Transfer function Bode plot

图5 干扰频谱图Fig.5 Interference spectrogram plot

系统的输入谱密度函数与干扰谱密度函数之间满足[10]：

(10)

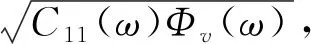
(a)过滤后输入时域图

(b)过滤后输出时域图图6 过滤后输入输出时域图Fig.6 Filtered input and output time domain plot

(a)输入谱密度对比

(b)输出谱密度对比图7 过滤前后输入输出谱密度对比Fig.7 Comparison of input and output spectral density before and after filtering

3 放电间隙电压预测模型

3.1 模型结构和阶次

经过预处理后的系统输入输出数据用于系统建模，对系统时域模型(式(4))和系统超前一步预报(式(5))进行进一步处理，分别得到系统模型和系统预测模型：

(11)

(12)

其中，B(q-1)、C(q-1)、D(q-1)、F(q-1)为延迟算子多项式；θ为系统模型参数。由式(11)和式(12)得到系统的预报误差：

(13)

引入辅助变量：

υ(t,θ)=y(t)-ω(t,θ)

由此得到系统的状态参数：

φ(t,θ)=(u(t-1),…,u(t-nb),-ω(t-1,θ),…
-ω(t-nf,θ),ε(t-1,θ),…,ε(t-nc,θ),
-υ(t-1,θ),…,-υ(t-nd,θ))T

则系统的预测模型方程(式(12))可写成：

(14)

θ=(b1,…bnb,c1,…cnc,d1,…dnd,f1,…fnf)T

系统的预报误差可以进一步表示为

ε(t,θ)=y(t)-φT(t,θ)θ

(15)

使用以下标量值函数表示预测误差的值：

(16)

根据最小二乘准则，得到以下最小二乘估计：

(17)

根据以上分析，对采集的数据进行预处理后，用输入、输出数据的前一半作为模型参数辨识数据，后一半数据验证模型的预测能力，进行系统预测模型的仿真、预测，确定电弧铣削加工间隙预测模型的最优模型为

(18)

B(q-1)=0.003 164q-1

C(q-1)=1+q-1

D(q-1)=1-2.684q-1+2.541q-1-1.03q-1+0.1726q-1

F(q-1)=1-1.987q-1+0.9907q-1

用得到的最优模型进行放电间隙电压拟合实验，实验过程在MATLAB软件中进行，将间隙电压预测模型得到的仿真值与加工过程中实时采集的放电间隙电压值进行拟合，0.5 s、1.5 s、2 s内的仿真输出值与放电间隙电压值拟合结果如图8所示。可以看出，随着拟合时间的增加，拟合精度逐渐降低，说明模型输出的仿真值与实际测得的间隙电压值的拟合程度只与拟合时间有关，拟合的时间段越短，拟合程度越高，因此，可以采用递推的方式实现对电弧铣削加工放电间隙电压的跟踪预测。

(a)0.5 s内

(b)1.5 s内

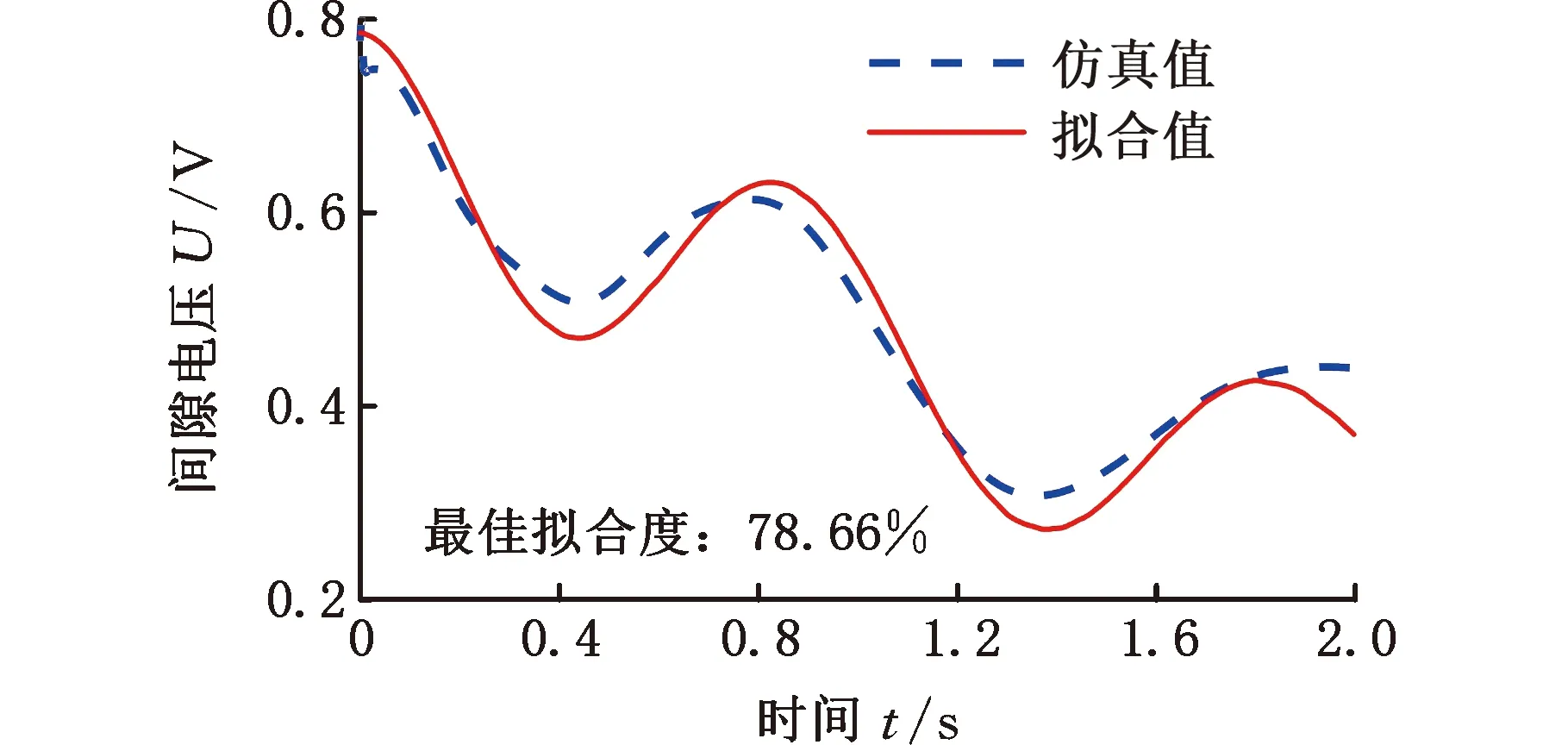
(c)2 s内图8 模型仿真值与间隙电压值拟合程度Fig.8 The degree of fit between the output of the prediction model and the measured discharge gap voltage

从控制的角度出发，需要比较预测模型与输入、输出数据所体现的系统传递函数特性相近的程度，因此，对电弧铣削加工间隙电压预测模型进行了频域分析，如图9所示，可以看到，预测模型与输入、输出数据的频域特性拟合较好，很好地反映了输入、输出数据的频域特性。另外，预测模型的零、极点分布合理，说明模型稳定性好，同时，模型的辨识参数少，因此，式(18)所表示的系统预测模型适用于电弧铣削加工系统，可以用于在线递推辨识。

(a)幅值

(b)相位图9 预测模型与输入、输出数据频域特性比较Fig.9 Comparison of the prediction model and input-output data in frequency domain characteristics

3.2 时变预测模型

前文已经确定了最优放电间隙电压预测模型的结构与阶数，并根据模型输出的仿真值与实际测量值的拟合结果得到的启示，用递推的方式将最优预测模型用于在线检测，此时模型的参数不再是常量，而是随加工过程发生变化。因此，式(18)用时变预测模型表示为

(19)

B(q-1)=b1q-1

C(q-1)=1+c1q-1

D(q-1)=1+d1q-1+d2q-2+d3q-3+d4q-4

F(q-1)=1+f1q-1+f2q-2

在电弧铣削加工过程中，需要根据加工过程进行估计的参数是θ=(b1,c1,d1,d2,d3,d4,f1,f2)T。参数的估计采用递推最小二乘算法计算：

(20)

另外，β(t,k)具有以下性质：

β(t,k)=λ(t)β(t-1,k),1≤k≤t-1

β(t,t)=1

因此，预测模型的完整递推辨识算法为

(21)

其中，λ(t)为遗忘因子，取λ=0.995。用预测模型的递推辨识算法对电弧铣削加工过程中的放电间隙电压进行实时预测，实验加工参数见表1。

表1 加工参数

实验过程中使用Handyscope HS4数据采集卡实时采集放电间隙电压，计算模型超前一步预测值与实际间隙电压值的平均预测误差，平均误差计算公式为

(22)

计算得到预测平均误差为6.82%。模型超前一步预测值与实际间隙放电电压值的对比如图10所示，为了更好地展示模型的预测能力。在图10中任选两部分进行比较，如图11所示，可以看到，预测模型能够跟踪间隙电压的变化，实时进行超前一步预测，由此得到以下结论：电弧铣削加工放电间隙电压预测模型具有很高的预测精度，为电弧铣削加工系统极间间隙的精确控制提供了理论依据和实践参考。

图10 预测模型的输出与实际间隙加工电压值比较Fig.10 Comparison between the output of the prediction model and the measured discharge gap voltage

4 结论

(1)本文建立了电弧铣削加工系统时域模型，对系统的输入输出数据进行谱密度分析，根据干扰频谱图，得到了输入输出数据的过滤频域为[0.003,0.5]，在此频域内过滤的数据满足系统建模的需求。

(a)a部分

(b)b部分图11 预测模型输出值与实际测量值详细比较Fig.11 Detailed comparison between the output of the prediction model and the measured discharge gap voltage

(2)用系统辨识方法确定了电弧铣削加工系统放电间隙电压预测模型的结构和模型参数，建立了放电间隙电压预测模型，并通过实验验证了模型的预测精度，0.5 s内预测精度为97.96%。

(3)基于放电间隙电压预测模型，采用递推最小二乘方法，实现了对放电间隙电压进行稳定的跟踪，预测模型能够超前一步预测放电间隙电压，预测平均误差是6.82%。

(4)本文预测模型能实时准确预测放电间隙电压，为放电间隙伺服控制提供准确依据，保证电弧铣削加工处于稳定、高效的加工状态。