机车轴箱双列圆柱滚子轴承损伤-振动模型及有限元模型的建立*

李 丹

（湖南铁道职业技术学院轨道交通机车车辆学院，湖南 株洲 412000）

1 研究背景

交通强国，铁路先行。铁路无疑是我国国民经济的“大动脉”。当前，铁路客货运量持续增长。2020年全国铁路旅客发送量完成22.03亿人，货运总发送量完成45.52亿吨，铁路运输占全国运输总量的9.9%，位居第三。机车在运输过程中占主要地位，位于机车转向架轮对轴箱的滚动轴承是保证运输安全的重要结构，其在运行过程中直接影响列车的平稳性及安全性。为了确保机车安全运行，对机车轴箱轴承性能的退化过程进行研究十分有必要。

众多学者对轴承的退化进行了研究，陈光东[1]对高速列车轴箱双列圆锥滚子轴承在不同载荷作用下的振动情况进行了分析，得到了不同故障点的轴承组成部件的振动频率值。董振振[2]通过对滚动轴承故障特点的分析，总结了一些常见故障位，并相应地建立了离散化的轴承故障振动模型，经过单点和复合损伤情形的模拟，完成了对所建立模型的验证。董绍江等[3]研究了轴承内圈局部损伤对轴承振动的影响，当轴承存在损伤时，转动过程中的损伤部分会对轴承的振动产生极大的增强作用，通过对振动频率的影响能够判断故障点的位置。程立等[4]采用了最大熵法和相似度法对滚动轴承的振动性能进行了研究，提出了一种轴承振动性能的退化模型，并确定了轴承退化与轴承保持可靠性之间存在明显的关系，但并未给出损伤后的模型。

以上研究并未涉及机车运行振动的过程，但损伤与振动是同时存在的，不间断的耦合会影响轴箱性能。牛乾[5]提出了有关旋转体损伤-振动耦合的概念，并详细阐述了其理论推导过程，为后续研究提供了参考，但暂未应用于具体案例，缺乏与实际情况的结合。宋宏智等[6]对损伤-振动作用下轴承的性能退化进行了理论推导与研究，有效量化并验证了损伤与振动的耦合关系，提出了轴承退化的三阶段理论。

课题组将具体针对高速列车轴箱双列圆柱滚子轴承进行理论推导，以得到该车型轴承的损伤-振动耦合理论模型、损伤有限元模型及初步的仿真结果，为后续接触特性及不同损伤程度的寿命预测提供依据。

2 圆柱滚子轴承损伤-振动数值模型

振动微分方程为：

式中，M为等效质量矩阵；C为等效阻尼矩阵；K为刚度矩阵，q为位移矩阵；F为等效载荷矩阵。

其空间矩阵形式如下：

其中，

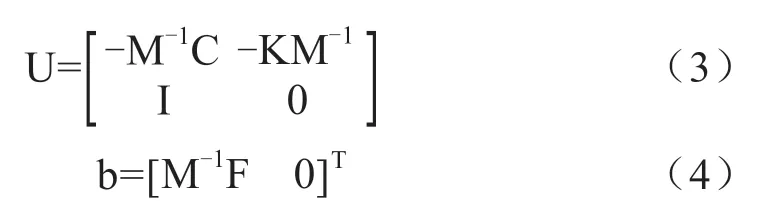
轴承部件满足旋转体的基本特征，其损伤演化微分方程如下：

其中H假设为可量化的损伤因子。在铁路轴承故障检测中，H通常可理解为点蚀脱落面积、裂纹深度、损伤程度等，即轴承部件损伤退化过程的映射关系。伴随轴承损伤退化程度的不断加深，参数M、C、K会发生一定程度的改变，并直接影响轴承部件刚度等性能参数，导致表面裂纹逐渐加深。

3 圆柱滚子轴承退化过程分析

3.1 轴承游隙与载荷分布

轴承内圈与实心轴完成装配关系时，内圈还会发生一定形变，原始游隙再次发生变化，最终引起因过盈配合产生的滚道直径变化。该变化量的大小与过盈量成正比，与内圈外径成正比，与内圈内径成反比。因此，轴承的游隙将变化为原始游隙与滚道直径变化量的差值。当轴承游隙发生变化时，其载荷分布也随之变化。

假设ψ为滚动体径向位置角，则当ψ=0°时，位移达到最大。对于径向载荷作用下的双列轴承，当两列轴承都承载时，根据静力平衡理论，则：

其求解式为：

式中，Kn为载荷-位移系数；δr为径向位移或接触变形；Pd为径向游隙；ε为载荷分布系数；Jr等参数通过误差控制试解法求解。

3.2 轴承载荷分布计算程序

根据轴承载荷分布计算理论与上节给出的计算方法，利用VB编程语言编制了用于计算圆柱滚动体轴承载荷分布的自动计算程序。计算程序的主界面如图1所示。

图1 参数设置界面

在滚子轴承基本参数模块，依次按照界面文本提示输入轴承相应的结构尺寸等参数。运用VB编制的圆柱滚动体轴承载荷分布的自动计算程序，提高了研究效率。

3.3 轴承内圈滚道裂纹与载荷分布的耦合关系

1）随着轴承内圈滚道裂纹的出现，轴承滚动体与内圈表面的接触状态以及内圈滚道的变形量将随之变化，而两者最终将体现在轴承游隙的变化量上。随着裂纹的不断加深，轴承游隙不断变化，此时轴承的承载情况也将直接受到影响。

假设轴承过盈量为λ，裂纹深度为h(t)，q为轴承内部应力载荷，游隙的变化量为Δd，内圈外径变化量为Δd1。当h(t)＞λ时，其值为0；当h(t)≤λ时，游隙变化量与损伤裂纹深度的关系可表示为：

此时轴承的载荷分布将变化为：

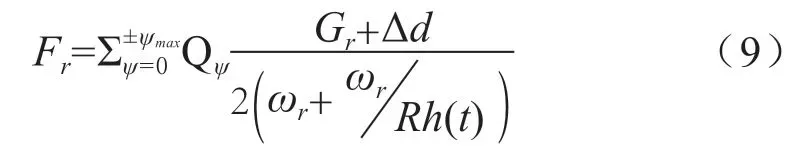
综上所述，轴承内圈裂纹会直接影响轴承的载荷分布情况，且有明确的数值关系。

2）假设轴承滚动体与滚道的接触刚度为K，则根据赫兹接触理论及滚动轴承振动微分方程，可以得到由于内圈引起的激振力与接触刚度的关系。同时接触刚度K还与轴承的载荷分布有关，在一定周期内轴承载荷稳定的工况下，轴承刚度也同样随之呈现一定规律的周期变化；在这一过程中，轴承的刚度也随轴承内圈裂纹深度的变化而发生一定改变，反过来裂纹的扩展同时受快速变化的内圈接触应力集中点的影响，裂纹与载荷相互影响，损伤与振动相互耦合。

4 损伤有限元模型的初步建立

根据现运行的高速铁路轴箱轴承样品，确定其结构尺寸，轴箱圆柱滚子轴承的主要参数及额定载荷如表1所示。

表1 轴承样品结构尺寸参数

按照表中数据初步建立研究对象的损伤有限元模型[7]。模型装配忽略了轴承的径向游隙、摩擦因素等的影响。假设研究对象处于退化初期，设定其裂纹宽度0.2 mm，长度10 mm，深度1 mm。为提高运算效率，对模型进行一定程度的简化切片，取最大受载部位滚动体与内外圈的对称面单侧6 mm切片进行研究。

利用ABAQUS有限元分析软件，对模型进行网格划分[8-10]，共生成50 231个C3D8R单元，89 413个结点。通过专用工具检查网格质量，发现全部满足有限元计算要求。根据样品轴承资料可知，其额定载荷为840 000 N。按照其额定轻载状态即20%进行计算，轴承径向载荷为21 467 N，有限元仿真结果之内圈表面接触应力云图如图2所示。轴承滚动体与内外圈等效应力云图如图3所示。由图3可知，模型最大等效应力为滚动体两端与内外圈滚道接触的部位，最大值约为1 476 MPa。

图2 内圈表面接触应力云图

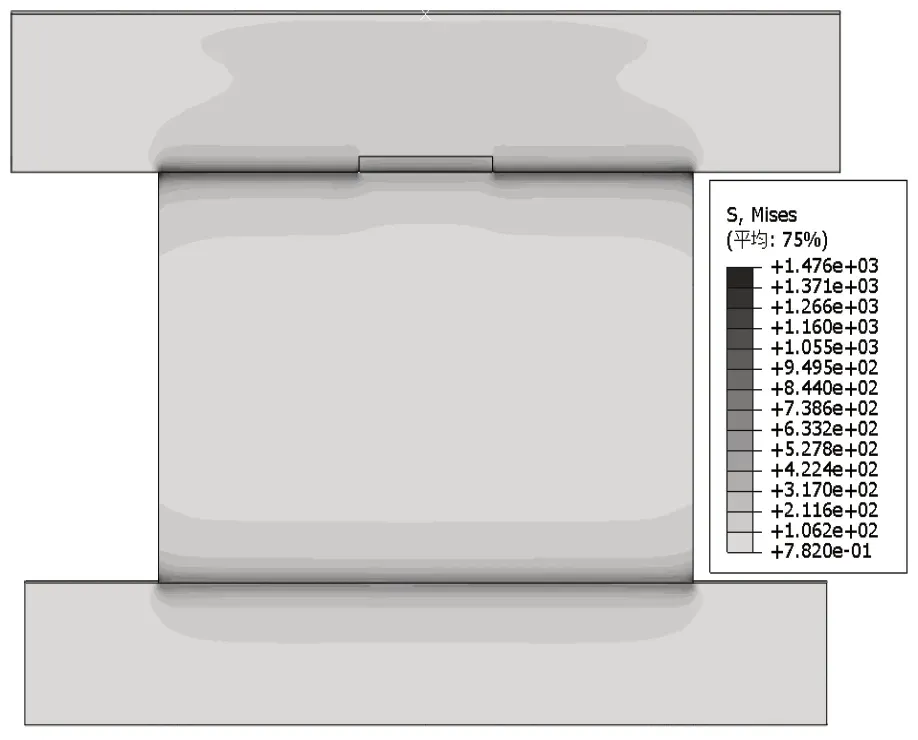
图3 轴承滚动体与内外圈等效应力云图

滚动体与内外圈接触中间与两端的各主要应力结果值如表2所示。滚动体与内圈最大接触应力出现在滚动体与内圈接触裂纹区域的两端，其最大值约为2 021 MPa，比滚道两侧应力高出562 MPa，约占38%；裂纹中部区域平均应力约为1 150 Mpa，比裂纹两端尖峰应力低871 Mpa。滚动体与外圈接触最大应力出现在接触两端，最大值约为1 545 MPa，高出中部平均应力约239 MPa，占比18%。

表2 滚动体与内外圈接触应力结果

综上可知，滚动体与内外圈滚道接触，损伤裂纹两端出现了最大边缘应力值，内外圈滚道两端也有应力尖峰，符合接触边缘效应理论；裂纹改变了原有滚道接触应力走势与最大应力值点，对接触应力造成了直接影响，同时应力集中的循环往复使裂纹不断扩展。

5 结论

课题组针对高速列车的双列圆柱滚子轴承进行了振动与退化模型的理论推导与分析，初步建立了该车型轴承的损伤-振动耦合理论模型，并建立了相应的损伤有限元模型，得到了损伤与应力相互影响的初步结论，为后续针对不同损伤程度的接触特性研究提供参考依据。