基于BP神经网络数控机床主轴电气故障诊断*

王书畅 ， 方 达

（1.湖北西塞山发电有限公司，湖北 黄石 435000；2.武汉交通职业学院，湖北 武汉 430065）

随着我国智能制造不断发展，数控机床作为制造的最终端，在生产加工中的作用日益增强。数控机床机械结构复杂，控制精度极高，若其发生故障，不仅会威胁生产人员的生命安全，还会对加工零件和机床本身造成损坏[1]。因此，研发人员在设计产品时有以下两方面的目标：首先，要保证数控机床安全稳定运行，尽量降低设备的故障率；其次，有在故障发生后快速判断故障类型的智能方法[2]。实现智能检测是企业亟需实现一项重大功能，同时也是实现智能制造的重要途径[3]。当前，常见的智能诊断方法有以下几种：模糊控制、专家系统、人工神经网络、基于向量机、故障树分析法、小波分析、粗集理论等[4]，本文主要使用BP神经网络进行故障诊断。

1 BP神经网络

人工神经网络简称神经网络，它是一种通过模仿动物神经网络行为从而建立分布式信息并行运算的数学模型。这种网络系统连接极其复杂，在处理信息时需要不断调整内部大量节点相互之间的连接关系。BP神经网络由Rumelhart和McClelland等人于1986年提出，是一种按照误差逆向传播算法训练的多层前馈神经网络，目前得到了广泛的应用。BP神经网络可以将任何复杂的模式进行分类，同时可以拟合任意非线性函数，其主要由输入层、隐含层和输出层组成[5]。图1为一个典型三层BP神经网络模型，层与层之间的元素相连，同一层不连，其中隐含层可以有多层。

图1 三层BP神经网络结构图

其中，X1，X2，X3，…，Xm代表输入层的输入参数，O1，Ok，…，On代表输出层的输出参数，ωij代表隐含层第i个节点连接输入层第j个节点间的权值，θi代表隐含层第i个节点的阈值，Φ代表隐含层的激励函数，ωki代表输出层节点到隐含层节点的权值，ak代表输出层第k个节点的阈值，Ψ代表输出层的激励函数，Ok代表输出层第k个节点的输出。在相邻的层之间有两个方向的信号在传递：一个是输入信号，主要从输入到输出方向传播，将输入通过隐含层和输出层进行计算；另一个是反向传播误差信号，主要用于修改权值和阈值从而减少误差。BP神经网络计算过程如下：

1）输入信号的前向传播原理。隐含层第i个节点的输入neti为：

隐含层第i个节点的输入Oi为：

输出层第k个节点的输入netk为：

输出层第k个节点的最后输出Ok为：

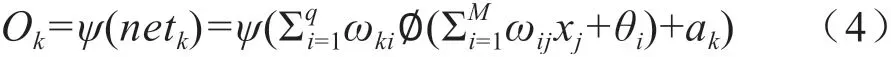
2）误差的反向传播。根据输出层的输出误差，计算出总误差。按照梯度下降法来调整各层的权值和阈值，使得最终的误差值能达到期望值。假设共有p个样本，则总误差函数为：

依据误差梯度下降法，依次计算隐含层的权值修正值Δωij和阈值修正值Δθi，然后计算输出层权值修正值Δωki和输出层阈值修正值Δa。

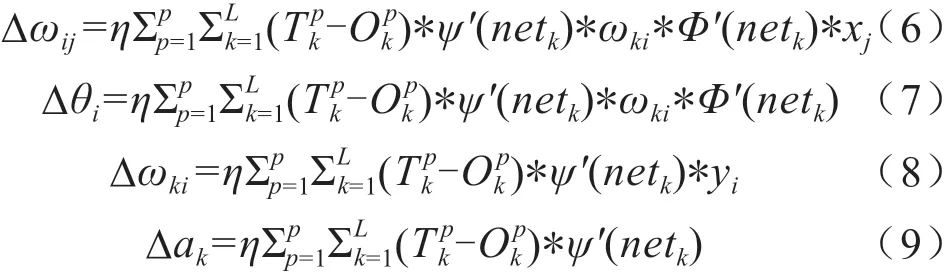
整个BP神经网络工作流程如图2所示。

图2 BP神经网络工作流程

BP神经网络具有简单、易于计算、并行性强等优点，现广泛用于神经网络训练中[6]，其本质是找到误差函数最小值的最优解。由于使用非线性算法中的最速下降法通过负梯度方向修改权值和阈值，故存在以下问题：首先是学习效率较低且收敛速度较慢，然后可能会陷于局部极小值附近，造成错误值。为解决该问题，使用附加动量法来进行修正[7]。附加动量法在BP神经网络修改权值和阈值时，不仅加上误差在梯度上的分量，同时还加上在误差曲面上的变化趋势。利用这个变化趋势，可以划过一些极小值，避免陷于其附近[8]。在没有附加动量的作用下，网络可能陷入浅的局部极小值，利用附加动量的作用则可能划过这些极小值。新的加上附加动量因子的权值和阈值调节公式为：

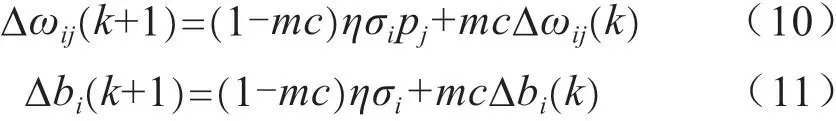
式中，k表示训练次数；mc表示动量因子，取0.95。

2 主轴电气故障平台

整个数控机床故障检测平台使用凯恩帝K2000MC(i)新一代总线式高档加工中心数控系统。本研究以该数控铣床加工中心为例，收集常见的主轴电气故障，分析对应的电气故障点，并一一列出。图3为本次使用的数控机床平台。

图3 凯恩帝数控机床故障检测平台

由图3可知，电路图中有很多电压检测点，通过采集电压可以判断故障类型及故障点。整个系统监测点很多，本研究选择与主轴电机相关部分。考虑到不同故障类型电压值变化较大，且比较依赖个人的分析能力，故尝试使用BP神经网络来进行自动判断。主轴部分电气控制图如图4所示。

图4 主轴部分电气控制图

主轴电气控制图主回路元器件包括隔离开关QS1、QS2、变压器、断路器QF1和接触器KM；二次回路包括QF2和接触器线圈KM。在图中数字位置设置电压采样点，在QS1后接线端1处采集平均电压，2处采集断路器QF1处平均电压，3处采集KM主触头后接线端电压，4处采集QS2后端平均电压，5处采集变压器交流电压，6处采集QF2后端电压。将统计的电压值使用归一法，将其值限制在0到1之间。表1为6种不同故障的训练样本。

表1 数控机床主轴电气故障训练样本

取输出向量Y表示故障产生的原因，具体如下：Y1为主电路没有通电；Y2为QF1没有正常接通； Y3为接触器主触头接触不良；Y4为刀开关没有完全闭合；Y5为变压器接触不良；Y6为QF2没有正常接通。故障训练样本的目标输出如表2所示。通过训练使目标尽量满足目标输出。

表2 故障训练样本目标输出

3 BP神经网络训练及验证

由表2可知，网络的输入层为6，输出层为6，根据经验公式确定隐含层为12。这里隐含层节点使用的传递函数为Sigmoid函数，输出层节点使用的传递函数为线性函数。网络训练函数采用梯度下降法和附加动量法两种方法，对比训练效果。网络的训练参数设置如下：

两种方法唯一的不同在于训练函数，梯度下降法使用的是traind，而附加动量法使用的是trainlm。

即最大训练次数为1 000，目标误差达到0.02。通过仿真得到梯度下降法的收敛效果如图5所示。

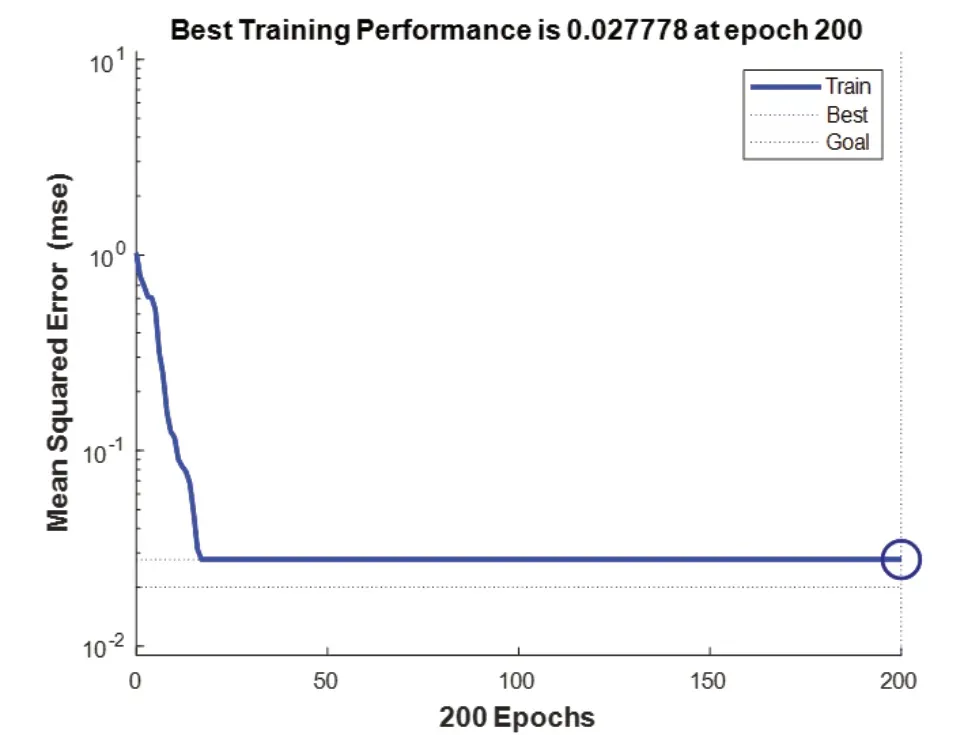
图5 梯度下降法的BP神经网络训练收敛图

由图5可知，梯度下降的BP神经网络在经过200次迭代后，网络的误差性能未达到期望的要求，误差最小为2.777 8×10-2。

附加动量法的BP神经网络训练收敛图如图6所示。由图6可知，附加动量法的BP神经网络在经过8次迭代后，训练输出的误差性能满足了期望的目标，并且误差最小为1.690 4×10-3。可见基于附加动量法的BP网络收敛速度很快。

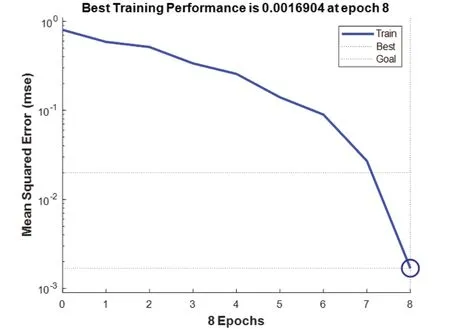
图6 附加动量法的BP神经网络训练收敛图

将图5与图6相比，可知基于附加动量法改进的BP神经网络比传统BP神经网络的收敛速度更快，并且避免了经典BP神经网络极易陷入局部极值的缺陷。故在数控机床主轴电气系统的故障诊断中，采用基于附加动量法的BP神经网络方法[9]。

针对完成训练好的BP网络，采集若干次主轴故障作为检验。输入向量x为：

则经过网络计算的故障向量y为：

与目标结果y=[0 1 0 0 0 0 ; 0 0 0 1 0 0]基本一致，与期望输出值相吻合，因此该模型可以满足诊断需求。

4 结束语

将神经网络算法应用于数控机床的电气故障诊断，是智能诊断的形式之一。将Matlab作为仿真平台，可以提高数控机床的控制精度和故障诊断准确度。伴随着数控技术和人工智能的发展，各种先进的故障诊断平台也会变得更加智能化，同时需要采集的信息也会越来越多。如何增加更多的信息、处理繁多的信息将会是未来数控机床故障诊断的趋势。将神经网络优势与其他算法相结合来提高诊断的速度和准确率，是今后的研究方向[10-11]。