基于系统电压分布曲线拟合的后备保护方案
2022-09-02宋国兵常娜娜侯俊杰常仲学郑玉平吴通华
宋国兵,常娜娜,侯俊杰,常仲学,郑玉平,吴通华
基于系统电压分布曲线拟合的后备保护方案
宋国兵1,2,常娜娜1,2,侯俊杰1,2,常仲学1,2,郑玉平3,4,吴通华3,4
(1.西安交通大学电气工程学院,陕西 西安 710049;2.电力设备电气绝缘国家重点实验室(西安交通大学),陕西 西安 710049;3.南瑞集团(国网电力科学研究院)有限公司,江苏 南京 211106;4.智能电网保护和运行控制国家重点实验室,江苏 南京 211106)
拓扑结构的多样性和电源特性的复杂性使得基于稳态电流量的后备保护整定工作量大且失配现象时有发生,无需整定且具有自动配合功能的后备保护技术是继电保护工作人员追求的目标。在分析了传统反时限过流保护存在的问题和辐射状配电网正、负序电压故障分量分布特征的基础上,提出了基于系统电压分布曲线拟合的后备保护方案。所提方案利用综合电压序分量的系统分布与各级保护实现逐级配合的最小动作时间拟合具有反时限特性的动作曲线,得出拟合后的分段函数表达式。由其计算的保护动作时间可自动反映各保护与故障位置的拓扑关联关系,在满足选择性和快速性要求的前提下实现各级保护的自适应配合。DG接入不会改变综合电压序分量的分布特征,因而所提方法对含DG的网络具有自适应性。理论分析和仿真结果表明,所提方法可自动实现任一点故障时上下级保护的快速、逐级配合。
后备保护;综合电压序分量;曲线拟合;自适应配合;DG接入
0 引言
电网结构的日趋复杂使得传统基于固定时间级差实现逐级配合的单端量后备保护整定工作量非常大,运行方式的灵活多变导致后备保护出现拒动、误动的情况时有发生[1-4]。已有的广域后备保护大都需要通信,通信技术的可靠性制约了广域后备保护的工程应用[5]。因此研究不依赖通信、无需整定动作时限和自适应故障位置的后备保护技术势在必行。
反时限保护根据动作量的大小自动调整动作时间,具有自适应故障严重程度的能力[6-7]。相比于阶梯式配合的电流保护,其能快速切除发生在靠近电源侧的故障,具有选择性优良和灵敏度高的特点,目前广泛应用于中低压配电网中[8-9]。
传统反时限过流保护及改进算法大都基于故障稳态电流。一方面,故障稳态电流不满足距故障点越近值越大的分布规律,而保护动作时间又与电流值的大小密切相关,导致整定和配合情况非常复杂[10]。另一方面,配电网中多采用标准反时限特性方程,其曲线变化率随横坐标值的减小而明显增大,当线路末端发生短路故障时,各级保护故障电流幅值减小,保护动作时间增长,上下级保护动作时间差值明显增大,从而对快速隔离故障产生不利影响[11]。
针对现有反时限过流保护存在整定复杂和配合困难的问题,已有研究主要分为以下两类。第一类是将主/后备保护对配合问题转化为优化问题,如:文献[12-15]利用遗传算法、粒子群算法及和声搜索算法等智能算法优化反时限参数;文献[16-17]利用二次规划技术等数学方法优化各级保护的启动电流和时间常数。优化方法减少了逐级整定的工作量,大大提升了保护的选择性和快速性,但目标函数的选取没有统一的表达形式,且无法从工程角度解释参数选择的合理性。第二类是通过引入其他电气量修正反时限过流保护方程,如:文献[18-19]引入故障电压标幺值;文献[11,20]引入测量阻抗或负荷阻抗。电压或阻抗的引入提升了DG接入时的保护性能,但并未解决整定计算工作量大的难题,反而进一步增加了整定工作量。
综上,有必要研究无需逐级整定且具有自动配合功能的后备保护技术。故障分量电压只在故障状态下出现,不存在保护死区问题,且分布规律与故障电压相反[21]。因此,如何应用故障分量电压在网络中的自然分布特征实现基于反时限特性的后备保护技术是值得深入研究的。
本文首先分析了传统反时限过流保护的基本原理及存在的问题,研究了辐射状配电网正、负序电压故障分量的分布特征,引入综合电压序分量以消除故障类型对电压幅值的影响。然后利用特定点故障时综合电压序分量的分布和理想的保护动作时间进行曲线拟合,得到具有反时限特性的分段函数,实现各级保护的自适应配合。并对DG接入的场景进行了适用性分析。最后在PSCAD中搭建仿真模型,验证了所提方法的有效性。
1 反时限过流保护基本原理及存在的问题
根据国际电工委员会IEC255-3标准的规定[22],反时限过流保护特性方程为

图1说明了辐射状电网配置反时限过电流保护时的配合情况。
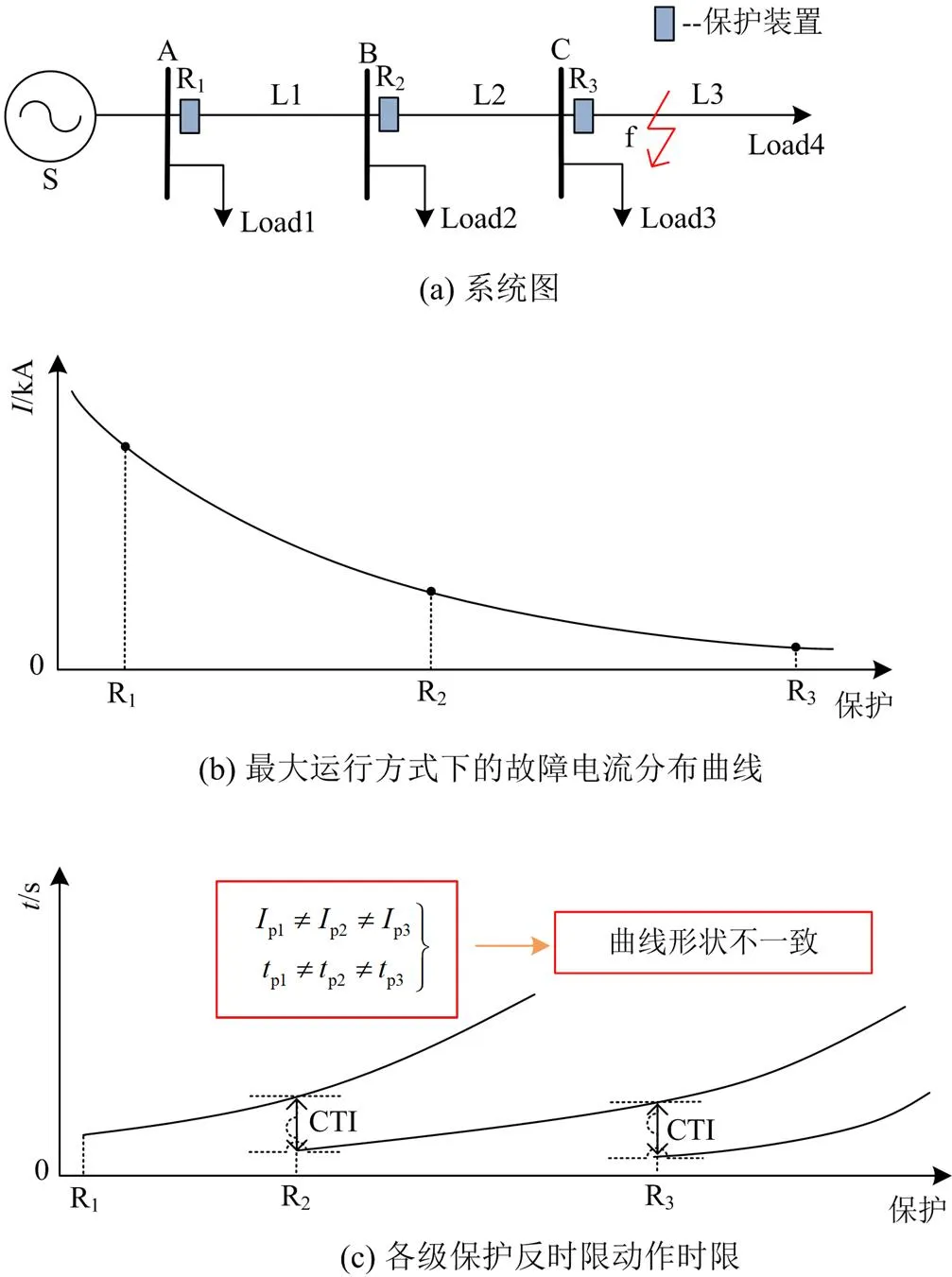
图1 反时限过电流保护配合情况
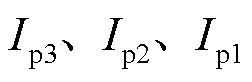
传统反时限过流保护作为本线路的主保护和相邻线路的后备保护,存在如下的问题:
1) 各级保护反时限特性参数必须通过逐级整定的方法得到,整定工作量大;
2) 基于离线整定的各级保护动作特性对DG接入不具有自适应性[23]。
因此,利用故障电流的分布特征无法构造全网采用统一反时限特性方程、自适应配合的后备保护。
2 正、负序电压故障分量的分布特征
配电网多为不接地或经消弧线圈接地系统,因此文中仅讨论f点发生相间短路故障时正、负序电压故障分量的分布特征。
2.1 三相短路的分布特征
三相短路时只有正序故障分量,图2为图1中f点发生三相短路时的正序故障分量附加网络。

图2 正序故障分量附加网络
故障后各母线电压降低,而负荷等效阻抗不变,导致流过负荷的故障电流减小,从而使得故障附加网络中各负荷的正序电流故障分量实际流向为由线路流向母线。由基尔霍夫电流定律可知,各保护装置正序电流故障分量的实际流向为由母线流向线路。
图2中的各保护正序电压故障分量可表示为
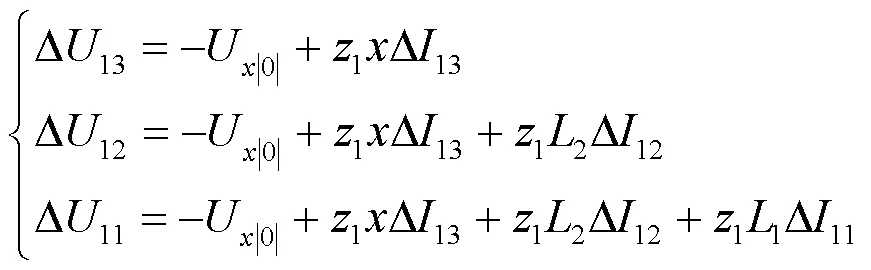
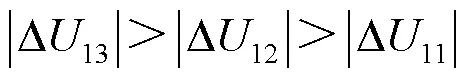
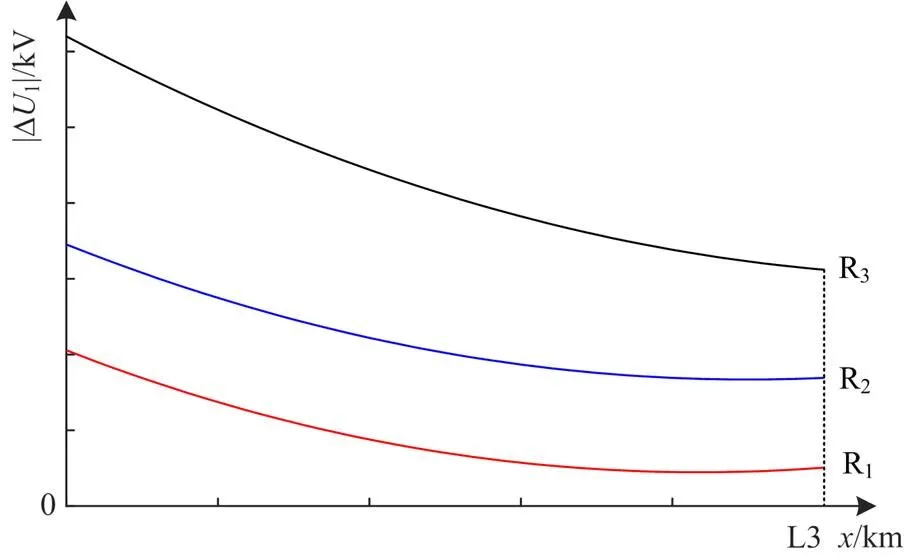
图3 正序电压故障分量分布特征
2.2 两相短路的分布特征
两相短路时正、负序故障分量都存在,其故障分量附加网络的复合序网如图4所示。

图4 故障分量附加网络的复合序网
图4中的各保护正、负序电压故障分量为
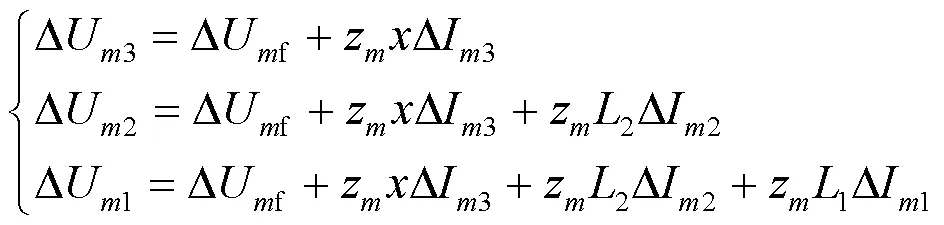
即两相短路时正、负序电压故障分量仍满足式(3)和图3的分布特征。

由式(4)、式(5)知,两相短路时各保护的正序电压故障分量与负序电压故障分量相等,即
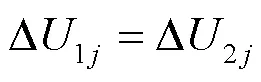
2.3 消除故障类型影响的综合电压序分量

表1 不同故障类型下f点的正、负序故障分量取值
由于两种故障类型下f点左侧等效网络相同,因而三相短路时各保护的正序电压故障分量工频幅值与同一位置下两相短路时正、负序电压故障分量工频幅值之和相等。
配电网经消弧线圈接地、f点发生两相短路接地故障时,故障分量附加网络的复合序网为正序、负序和零序三个序网在故障点的并联,正、负序电流和电压故障分量分别为
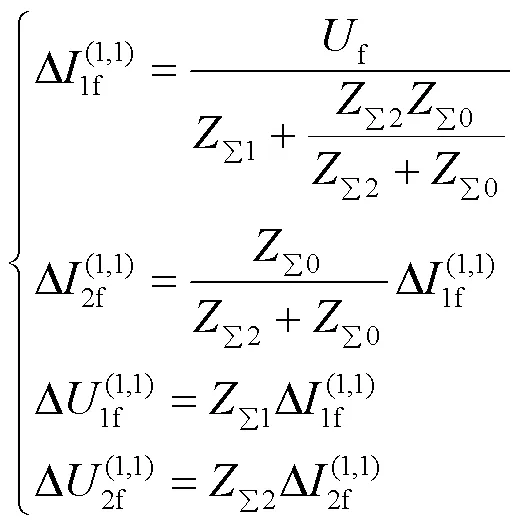
则有

即当两相短路接地时,各保护的正、负序电压故障分量之和也与三相短路时相等。
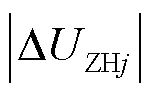

数值相加不改变新数据的分布特征,因而各保护综合电压序分量仍满足式(3)的分布特征。
综上,正、负序电压故障分量的分布特征如下:
1) 当相间短路故障时,各级保护的正、负序电压故障分量均满足距故障点越近、值越大的特点,其自然的阶梯分布规律可直接反映故障严重程度;
2) 构造综合电压序分量以消除故障类型对保护输出的影响,为实现统一反时限特性方程的后备保护提供理论基础。
3 基于系统电压分布曲线拟合的后备保护方案
反时限后备保护依据自适应故障位置的各级保护逐级动作以隔离故障,定位为本级线路瞬时电流速断的近后备保护和相邻下级线路的远后备保护,最小动作时间取0.5 s。为实现全网任一点故障时各保护同时满足选择性和快速性要求,本文引入曲线拟合的方法。
3.1 保护启动判据
为防止故障点下游和无故障支路无选择性动作、工业负荷投切(如大型电动机)引起保护误启动,本文同时引入电流、电压构造保护启动判据。

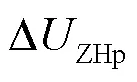
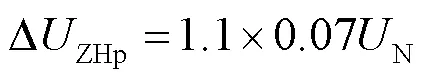
即式(10)、式(11)共同构成了后备保护方案的启动判据。
3.2 各级保护出口故障时满足选择性要求的实现方法
各条线路首端发生金属性短路故障时电压跌落最严重,且故障点越靠近系统侧,综合电压序分量值越大。因此,拟利用传统标准反时限特性方程构造基于综合电压序分量的反时限方程,以实现各级保护出口故障时的选择性要求。保护特性方程为
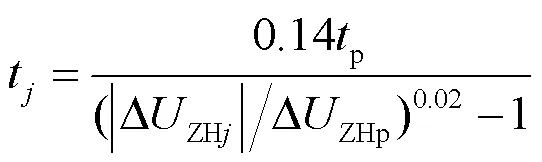

3.3 曲线拟合依据


表2给出线路L1首端、最末一级线路L3首端和末端分别故障时保护R1—R3对应的综合电压序分量、理想动作时间。利用这3个故障位置的7个离散点,实现基于系统电压分布特征的曲线拟合。

表2 不同故障位置下保护取值
3.4 曲线拟合
为保证上下级保护的绝对选择性,拟合后的曲线应位于原有配合关系的两离散点连线的上方,同时应保证拟合后曲线斜率大于原曲线斜率。因此,曲线拟合满足的不等式约束为
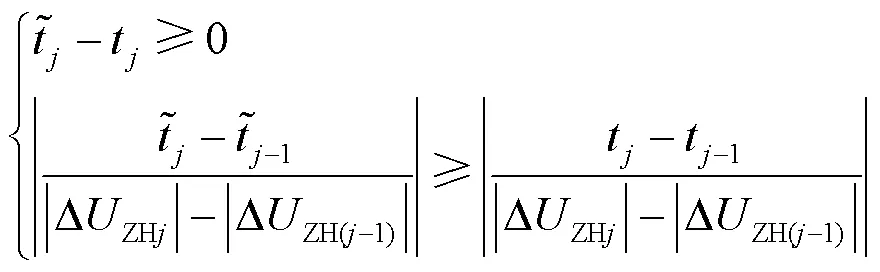
曲线拟合实现步骤如下:
1) 将最末一级线路首端故障时各保护对应的离散点用折线连接,如图5中黑色实线所示;
2) 将最末一级线路末端故障时各保护对应的离散点用折线连接,如图5中红色虚线所示;
3) 比较步骤1)、步骤2)中两折线的位置,将位于下方的折线向上平移至最下面的离散点位于上方折线段上,如图5中将红色虚线向上平移至红色实线的位置,得到L3末端故障时的修正数据;
4) 由蓝色三角点①、黑色实线上的点②、红色实线上的点③、④、⑤共同组成了曲线拟合的边缘点,各点已标注于图5中;
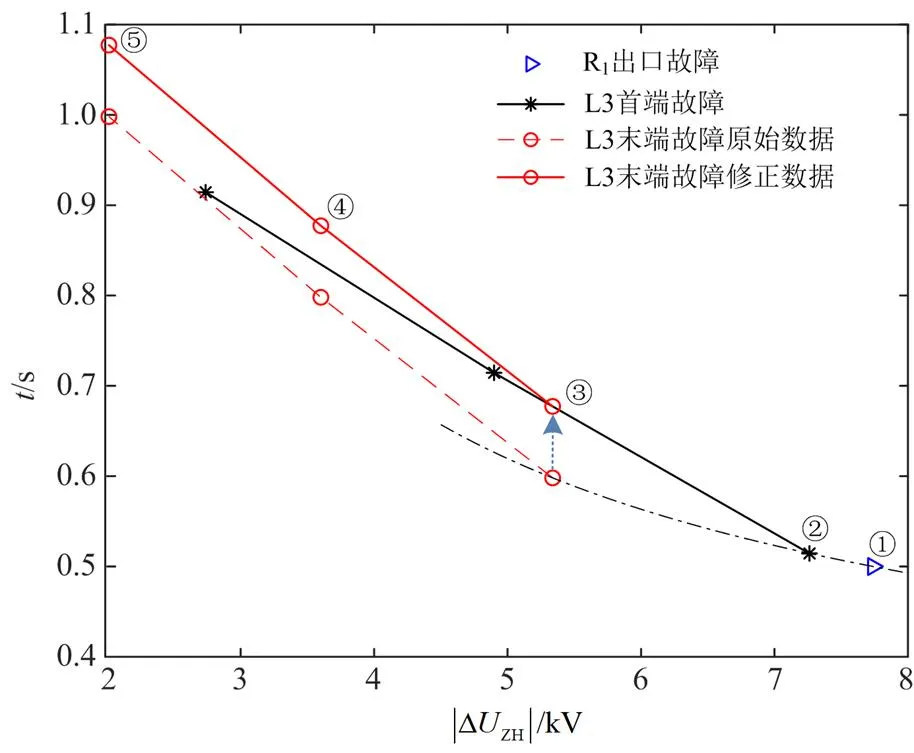
图5 曲线拟合过程
末端故障时各保护综合电压序分量差值小于首端,则全网采用相同的CTI取值时,末端故障时相邻上下级保护间连线的斜率大于首端故障,进一步说明采用如上步骤实现曲线拟合满足选择性要求。
当网络中有多条馈线时,既可将所有馈线按上述步骤进行拟合,得出全网适用的函数表达式;也可将每条馈线分别进行拟合,得出同一馈线上各保护适用的函数表达式。
3.5 后备保护方案的实现
曲线拟合是通过选取特定故障点离线得到的。当网络中任一点发生短路故障时,满足式(10)和式(11)的保护根据拟合的分段函数表达式计算后备保护动作时间。当主保护拒动或断路器失灵时,达到计算的保护动作时间后后备保护延时动作,实现基于反时限特性的后备保护功能。保护流程图如图6所示。
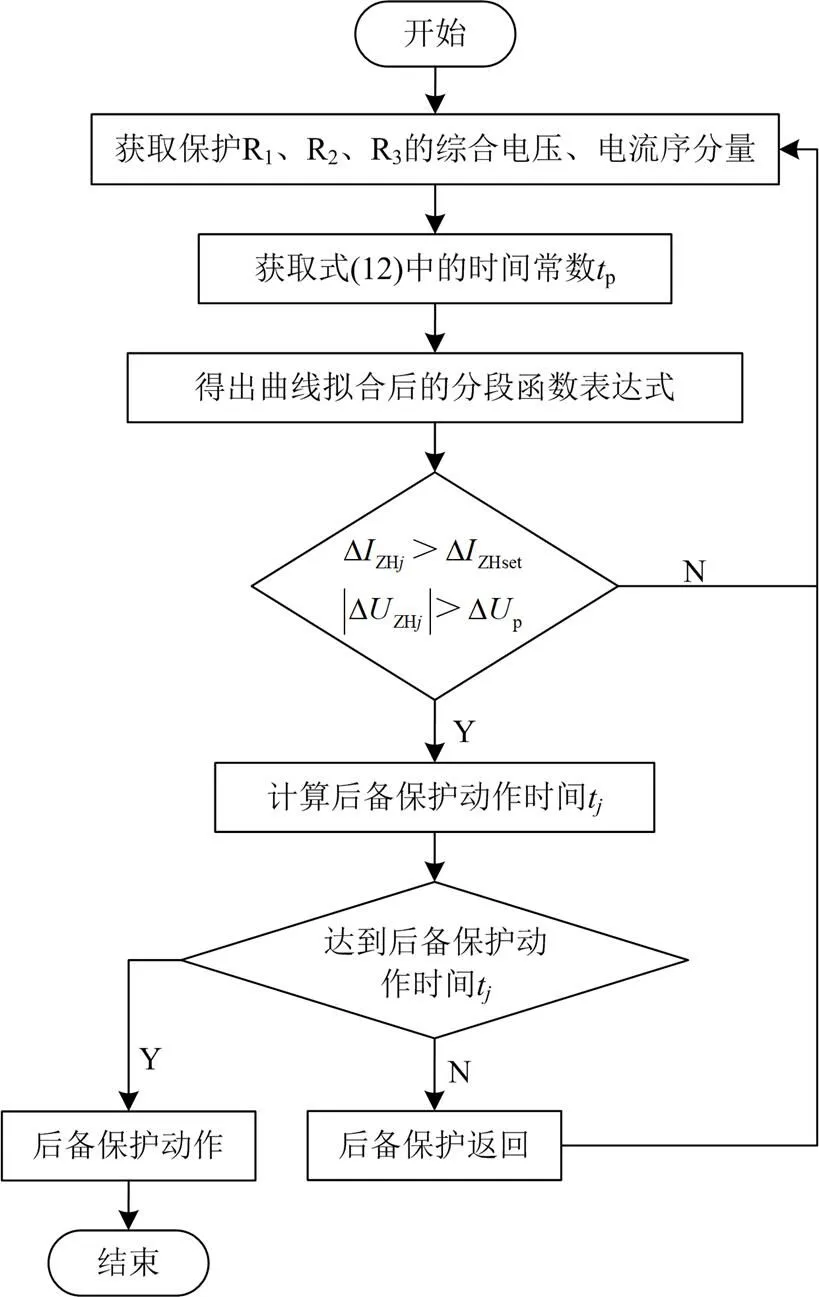
图6 保护流程图
4 保护适应性分析
4.1 DG接入的适应性分析
分布式电源的接入改变了故障电流的分布特征,使得传统反时限过流保护的灵敏度降低,甚至出现保护误动或拒动的可能性[26]。因此,需分析DG接入对各保护故障分量电压系统分布的影响。
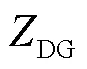


DG接入后,各保护正序电压故障分量为
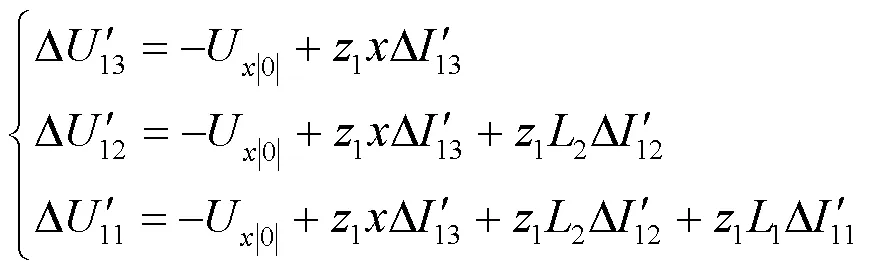
即线路压降使得各保护正序电压故障分量仍满足式(3)的分布特征。
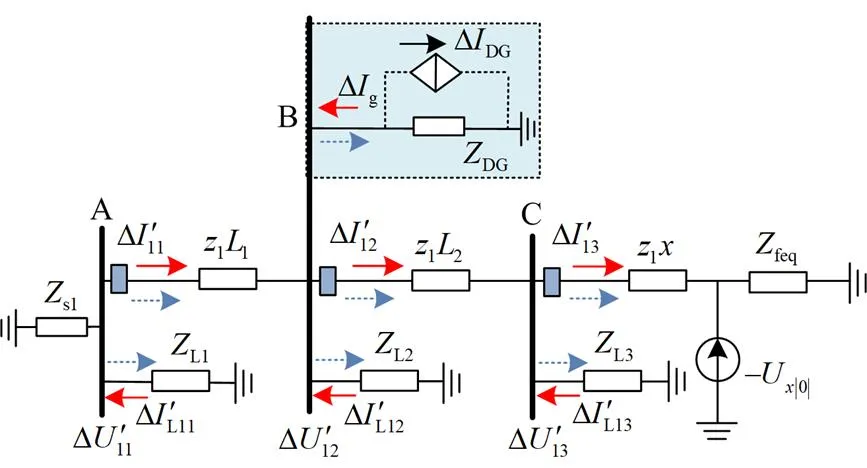
图7 母线B上接入DG时的正序故障分量附加网络
尽管正序故障分量控制下的DG只输出正序电流故障分量,导致两相短路时正、负序故障分量附加网络略有差异,但考虑DG输出的弱馈性,本文近似认为两相短路时各保护综合电压序分量工频幅值与三相短路时是相等的。因此,DG接入不改变综合电压序分量的分布特征,本文所提方法对含DG的网络具有自适应性。
4.2 拓扑结构变化时的适应性分析
利用距故障点越近、值越大的综合电压序分量实现了基于系统电压分布曲线拟合的后备保护方案,本质上是依据线路压降实现的自适应配合。故所提方案对以故障点为源端、综合电压序分量因网络拓扑呈现自然差异的拓扑结构是具有自适应性的,如双电源供电系统(需借助方向元件)和含高渗透率DG的配电网。但拓扑结构不同,各保护综合电压序分量的大小和相邻上下级保护间综合电压序分量的差值也不同,因此应根据当前拓扑结构得出对应的拟合曲线,实现同时满足选择性和快速性要求的后备保护功能。另外,拟合曲线是依据固定拓扑得到的,且是全网适用的,因此当网络中某条线路退出运行导致拓扑结构发生较小变化时,就地保护装置可自适应拓扑结构的变化。
5 仿真验证
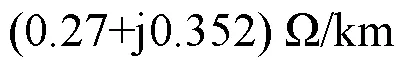
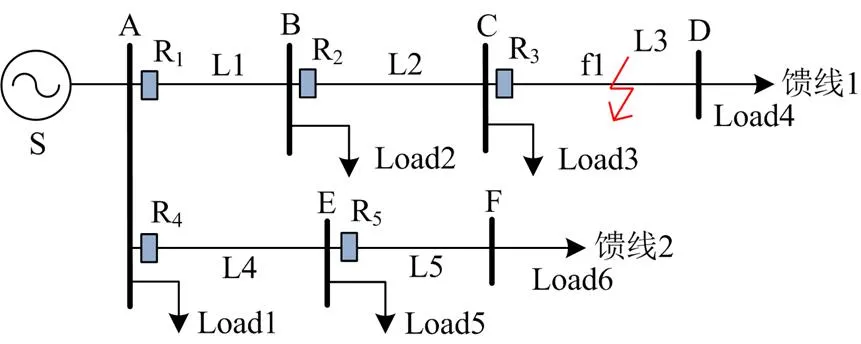
图8 配电网仿真模型
本文采用全周相减法得到故障分量电压、电流,然后对其进行快速傅里叶变换计算正、负序电压和电流故障分量,取故障后第3个周波数据的平均值作为综合电压、电流序分量的测量值。
5.1 不同故障位置下的仿真分析
根据3.4节曲线拟合步骤,CTI = 0.2 s时得出馈线1拟合后的分段函数表达式,如式(16)所示。
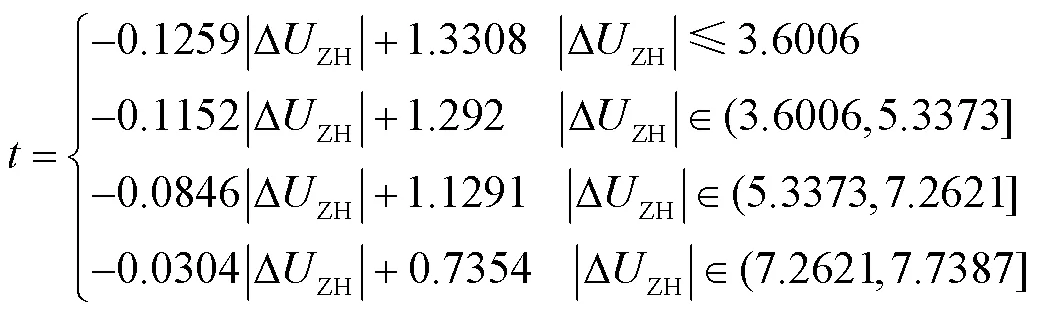
图9为线路L3中点分别发生三相短路和两相短路时各保护故障分量电压分布情况。三相短路的正序电压故障分量和两相短路的正、负序电压故障分量均遵循距故障点越近、值越大的分布规律,且两种故障类型下各保护综合电压序分量幅值是相等的,验证了理论分析的正确性。
各保护动作时间由自适应故障严重程度的分段函数计算得到,且动作时间的大小自动反映各保护与故障位置的关联关系。具有逐级配合关系的各保护动作时间差值基本都在CTI取值附近。与阶段式配合的过流保护相比,曲线拟合得到的具有反时限特性的分段函数可快速切除靠近电源侧的故障。
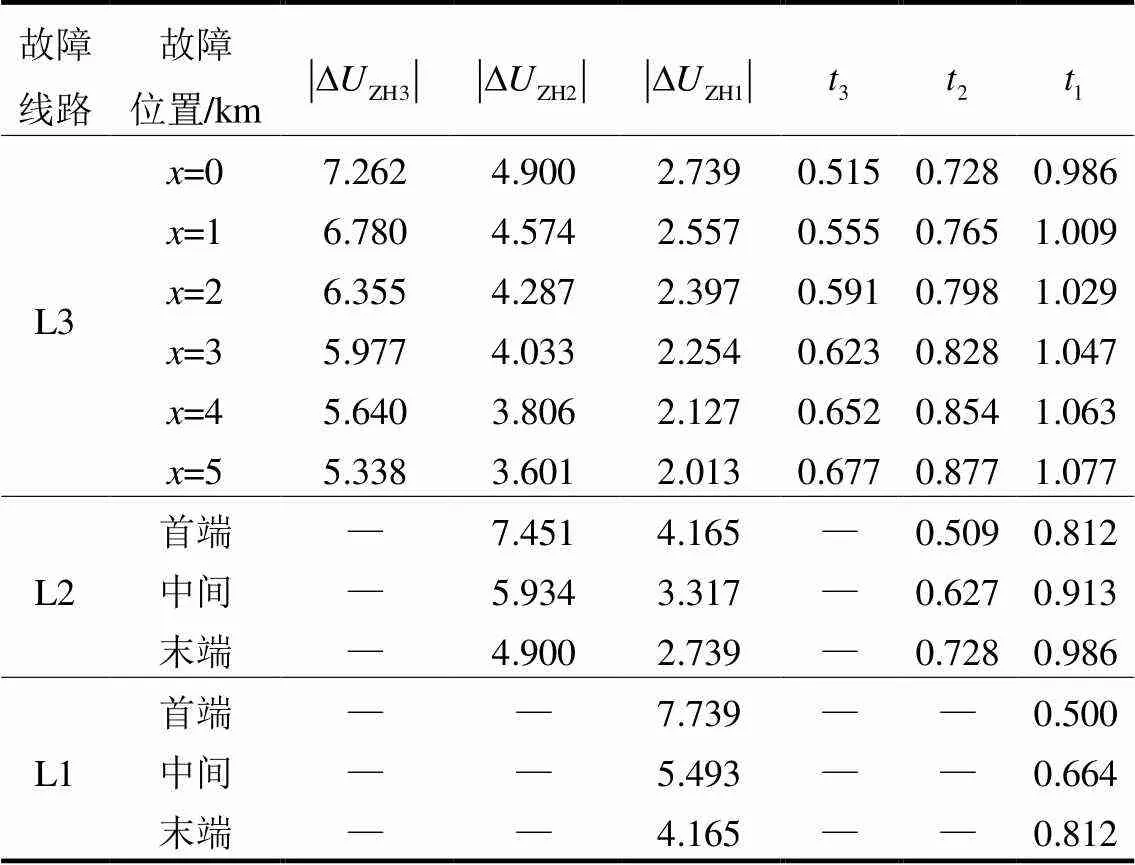
表3 不同故障位置下的各级保护动作情况
5.2 过渡电阻对保护性能影响分析
由图10可知,与金属性短路故障相比,当经过渡电阻短路时,各保护综合电压序分量幅值减小,相邻上下级保护综合电压序分量差值也减小,保护动作时间增大、相邻上下级保护动作时间差值减小,导致保护失去选择性。
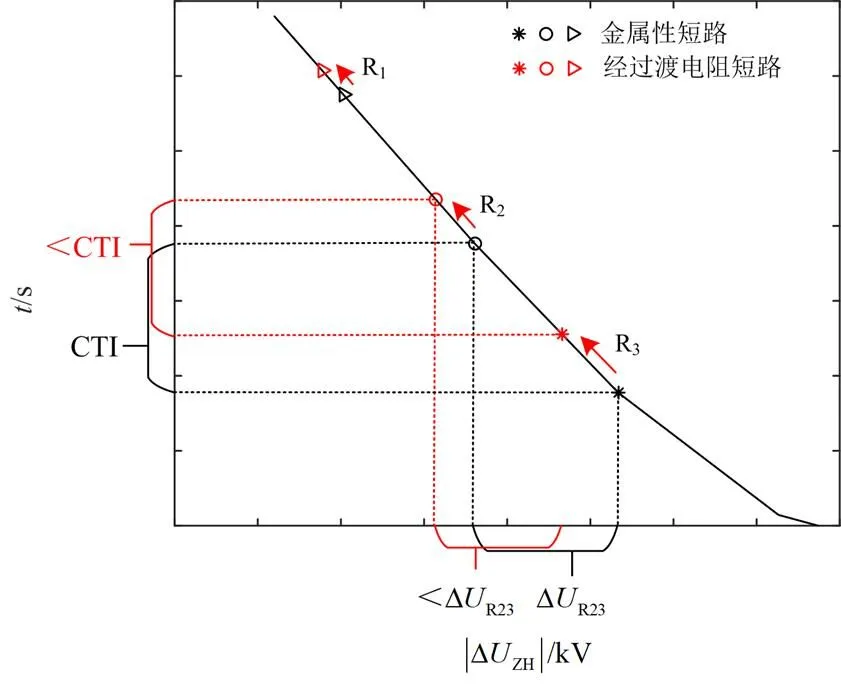
图10 过渡电阻对保护性能的影响
工程应用中选取特定点进行曲线拟合时,可在拟合过程中通过适当提高各拟合点动作时间差值的方法提升耐过渡电阻能力。图11为CTI = 0.2 s和CTI = 0.3 s时对应的拟合后分段函数曲线,并给出了线路L3末端经5 Ω电阻短路时,各保护综合电压序分量取值和动作时间。对比两曲线上的保护动作时间可知,拟合时增大CTI可保证经过渡电阻短路时的保护选择性。

图11 不同CTI取值时拟合的分段函数曲线
5.3 改变线路长度、CTI取值时的保护性能分析
图12为L1 = 3 km、L2 = 2 km、L3 = 4 km及CTI = 0.3 s时的曲线拟合情况。

图12 改变线路长度和CTI取值时的曲线拟合情况
由式(2)可知,各保护综合电压序分量幅值会受线路长度、故障位置的影响,而所提方案进行曲线拟合时考虑了最末一级线路首、末端故障时的场景,也就将线路长度、故障位置对保护性能的影响计及到离线计算的保护算法中,因而所提方案对线路长度具有自适应性。
CTI取值增大时,相邻上下级保护动作时间差值的裕度增大,拟合后各分段函数的斜率均增大,导致所提方案作为近后备保护时的动作时间明显增大。因而应结合断路器动作特性、保护性能要求选取合适的CTI值。
5.4 DG接入的仿真分析
以逆变类DG接入图8的母线B、C为例分析所提方案对DG接入的适用性。正常运行时DG的额定功率分别为0.5 MVA、1 MVA。CTI = 0.2 s时拟合的分段函数表达式如式(17)所示。

表4给出线路L3在不同故障位置发生三相短路和两相短路时的各级保护动作情况。
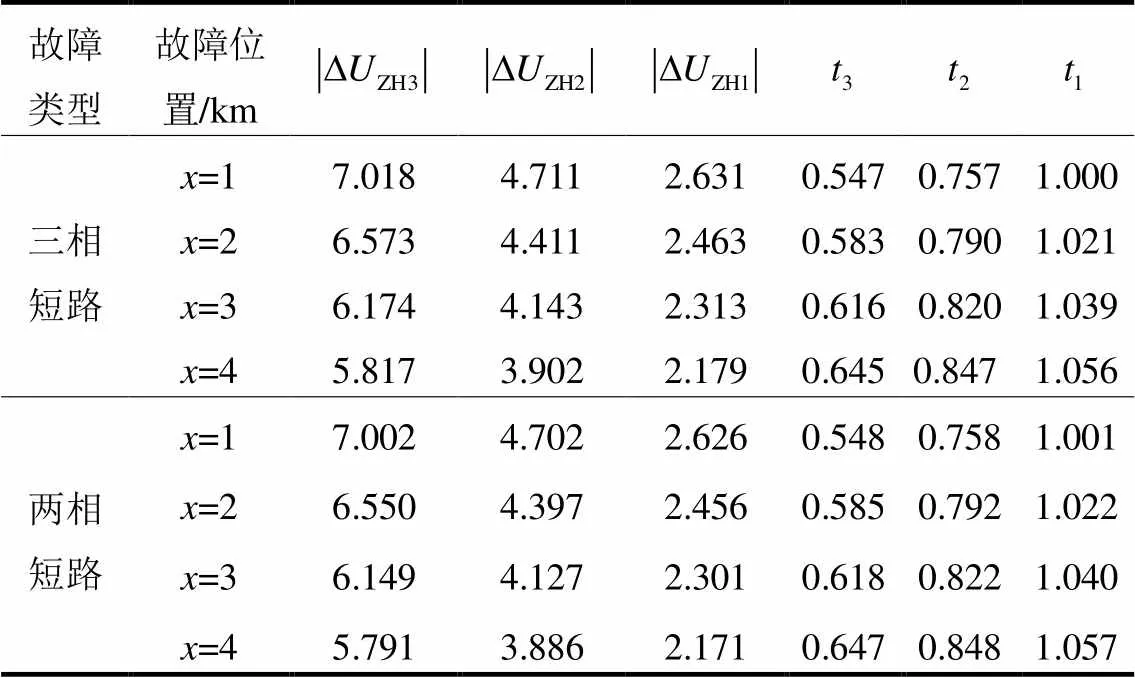
表4 不同故障位置、不同故障类型下的各级保护动作情况
DG接入后各保护的综合电压序分量仍满足图3的自然分布规律,且两相短路时综合电压序分量的幅值与三相短路时基本相等。各级保护动作时间由式(17)计算得到,差值均满足CTI要求,因此所提方法对DG接入的网络具有自适应性。
6 结论
本文分析了辐射状配电网在不同故障类型下正、负序电压故障分量的分布特征,引入综合电压序分量,提出了基于系统电压分布曲线拟合的后备保护方案。所提方案无需逐级整定、具有自适应配合能力,理论分析和仿真验证得出如下结论:
1) 综合电压序分量具有距故障点越近、幅值越大的特点,且在不同故障类型下输出值相同,是实现基于曲线拟合后备保护方案的理论基础;
2) 依据指定点的电压信息和理想动作时间得出分段函数表达式,实现任一点故障时各级保护自适应故障位置的动作排序,无需通信;
3) 拟合过程中适当提高各拟合点动作时间差值,以提升保护抗干扰和耐受过渡电阻能力;
4) 当网络中某种电气量具有距故障点越近、值越大的自然分布规律时,均可采用曲线拟合方法实现同时满足选择性和快速性要求的保护方案。
[1] 马静, 李金龙, 王增平, 等. 基于故障关联因子的新型广域后备保护[J]. 中国电机工程学报, 2010, 30(31): 100-107.
MA Jing, LI Jinlong, WANG Zengping, et al. Wide-area back-up protection based on fault correlation factor[J]. Proceedings of the CSEE, 2010, 30(31): 100-107.
[2] 王睿, 王晓茹, 黄飞, 等. 基于相关矩阵的电网广域后备保护算法[J]. 电力系统自动化, 2013, 37(4): 69-74.
WANG Rui, WANG Xiaoru, HUANG Fei, et al. Wide area backup protection algorithm for power grid based on correlation matrix[J]. Automation of Electric Power Systems, 2013, 37(4): 69-74.
[3] 田聪聪, 文明浩. 具有高信息冗余的广域后备保护系统[J]. 电网技术, 2011, 35(10): 214-219.
TIAN Congcong, WEN Minghao. A wide-area backup protection system with high information redundancy[J]. Power System Technology, 2011, 35(10): 214-219.
[4] 童晓阳, 张生鹏, 张广骁. 基于区域PMU和节点故障注入电流的广域后备保护算法[J]. 电力系统自动化, 2021, 45(15): 158-165.
TONG Xiaoyang, ZHANG Shengpeng, ZHANG Guangxiao. Wide-area backup protection algorithm based on regional phasor measurement unit and nodal fault-injection current[J]. Automation of Electric Power Systems, 2021, 45(15): 158-165.
[5] 金能, 梁宇, 邢家维, 等. 提升配电网线路保护可靠性的远方保护及其与就地保护优化配合方案研究[J]. 电工技术学报, 2019, 34(24): 5221-5233.
JIN Neng, LIANG Yu, XING Jiawei, et al. Research on remote protection and the optimized coordination scheme of local-remote protection to enhance the protection reliability of the line in distribution network[J]. Transactions of China Electrotechnical Society, 2019, 34(24): 5221-5233.
[6] 喻锟, 林湘宁, 李浩, 等. 考虑分布式电源稳定助增效应的电压修正反时限过电流保护方案[J]. 中国电机工程学报, 2018, 38(3): 716-726.
YU Kun, LIN Xiangning, LI Hao, et al. A voltage correction based inverse-time overcurrent protection scheme considering distributed generation stable infeed effect[J]. Proceedings of the CSEE, 2018, 38(3): 716-726.
[7] 曹喆, 季亮, 常潇, 等. 基于复合故障补偿因子的微电网反时限电流保护方法[J]. 电力系统保护与控制, 2020, 48(20): 133-140.
CAO Zhe, JI Liang, CHANG Xiao, et al. Inverse-time current protection method of a microgrid based on a composite fault compensation factor[J]. Power System Protection and Control, 2020, 48(20): 133-140.
[8] 黄景光, 张宇鹏, 李江峡, 等. 基于阻抗修正的反时限过流保护新方案[J]. 电力系统保护与控制, 2020, 48(9): 88-94.
HUANG Jingguang, ZHANG Yupeng, LI Jiangxia, et al. A novel impedance correction-based inverse-time overcurrent protection scheme[J]. Power System Protection and Control, 2020, 48(9): 88-94.
[9] 韦嘉, 柏瑜, 熊兰, 等. 反时限过流保护模型优化与曲线交叉研究[J]. 电测与仪表, 2015, 52(9): 56-60, 65.
WEI Jia, BAI Yu, XIONG Lan, et al. Research of inverse time overcurrent protection model optimization and curve intection[J]. Electrical Measurement & Instrumentation, 2015, 52(9): 56-60, 65.
[10]张保会, 尹项根. 电力系统继电保护[M]. 2版. 北京: 中国电力出版社, 2009.
[11]黄文焘, 邰能灵, 杨霞. 微网反时限低阻抗保护方案[J]. 中国电机工程学报, 2014, 34(1): 105-114.
HUANG Wentao, TAI Nengling, YANG Xia. Inverse-time low-impedance protection scheme for microgrids[J]. Proceedings of the CSEE, 2014, 34(1): 105-114.
[12] ALKARAN D S, VATANI M R, SANJARI M J, et al. Optimal overcurrent relay coordination in interconnected networks by using fuzzy-based GA method[J]. IEEE Transactions on Smart Grid, 2018, 9(4): 3091-3101.
[13]袁荣湘, 陈彧, 吴昊. 采用PSO算法的反时限过流保护配合方法[J]. 高电压技术, 2009, 35(7): 1730-1735.
YUAN Rongxiang, CHEN Yu, WU Hao. Method of inverse-time overcurrent protection coordination using PSO algorithm[J]. High Voltage Engineering, 2009, 35(7): 1730-1735.
[14]杨克杰, 黄纯. 配电网反时限过电流保护优化整定方法[J]. 电力自动化设备, 2019, 39(3): 163-168.
YANG Kejie, HUANG Chun. Optimal setting method of inverse time over-current protection for distribution network[J]. Electric Power Automation Equipment, 2019, 39(3): 163-168.
[15]何思名, 袁智勇, 雷金勇, 等. 基于改进灰狼算法的DG 接入配电网反时限过电流保护定值优化[J]. 电力系统保护与控制, 2021, 49(18): 173-181.
HE Siming, YUAN Zhiyong, LEI Jinyong, et al. Optimal setting method of inverse time over-current protection for a distribution network based on the improved grey wolf optimization[J]. Power System Protection and Control, 2021, 49(18): 173-181.
[16] BIRLA D, MAHESHWARI R P, GUPTA H O. A new nonlinear directional overcurrent relay coordination technique, and banes and boons of near-end faults based approach[J]. IEEE Transactions on Power Delivery, 2006, 21(3): 1176-1182.
[17] EZZEDDINE M, KACZMAREK R, IFTIKHAR M U. Coordination of directional overcurrent relays using a novel method to select their settings[J]. IET Generation, Transmission & Distribution, 2011, 5(7): 743-750.
[18] SALEH K A, ZEINELDIN H H, AL-HINAI A, et al. Optimal coordination of directional relays using a new time-current-voltage characteristic[J]. IEEE Transactions on Power Delivery, 2015, 30(2): 537-544.
[19] SINGH M, AGRAWAL A. Voltage-current-time inverse- based protection coordination of photovoltaic power systems[J]. IET Generation, Transmission & Distribution, 2019, 13(6): 794-804.
[20]刘玉娟, 卫志农, 孙国强, 等. 低阻抗加速反时限过电流保护[J]. 电网技术, 2019, 43(9): 3424-3431.
LIU Yujuan, WEI Zhinong, SUN Guoqiang, et al. Low impedance acceleration inverse-time over-current protection[J]. Power System Technology, 2019, 43(9): 3424-3431.
[21]葛耀中. 新型继电保护与故障测距原理与技术[M]. 2版. 西安: 西安交通大学出版社, 2007.
[22] IEC Publication 255-3 single input energizing quantity measuring relays with dependent or independent time[S]. Second Edition, 1989.
[23]谢民, 王同文, 徐靖东, 等. 分布式电源对配网继电保护影响及综合改进保护方案[J]. 电力系统保护与控制, 2019, 47(19): 78-84.
XIE Min, WANG Tongwen, XU Jingdong, et al. Influence of distributed power supply on distribution network relay protection and comprehensive improvement protection scheme[J]. Power System Protection and Control, 2019, 47(19): 78-84.
[24]李哲, 张保会. 一种利用序分量原理提高电流保护灵敏度的算法[J]. 电力系统自动化, 2000, 24(1): 26-29.
LI Zhe, ZHANG Baohui. A new theory to improve the sensitivity of current protection by sequence components[J]. Automation of Electric Power Systems, 2000, 24(1): 26-29.
[25]林海雪. 电能质量国家标准系列讲座第1讲供电电压偏差标准[J]. 建筑电气, 2011, 30(4): 3-9.
LIN Haixue. Lectures on national standard of power quality lecture one standard of supply voltage deviation[J]. Building Electricity, 2011, 30(4): 3-9.
[26]周卫, 张尧, 夏成军, 等. 分布式发电对配电网继电保护的影响[J]. 电力系统保护与控制, 2010, 38(3): 1-5, 10.
ZHOU Wei, ZHANG Yao, XIA Chengjun, et al. Effect of distributed generation on relay protection of distributed system[J]. Power System Protection and Control, 2010, 38(3): 1-5, 10.
[27] WANG P, SONG J, LIANG F, et al. Equivalent model of multi-type distributed generators under faults with fast-iterative calculation method based on improved PSO algorithm[J]. Protection and Control of Modern Power Systems, 2021, 6(3): 371-382.
[28]中国电力科学研究院有限公司, 阳光电源股份有限公司, 华为技术有限公司. 光伏发电并网逆变器技术要求: GB/T 37408—2019[S]. 北京: 中国标准出版社, 2019.
China Electric Power Research Institute, Sungrow Power Supply Co., Ltd., Huawei Technologies Co., Ltd. Technical requirements for photovoltaic gird-connected inverter: GB/T 37408—2019[S]. Beijing: Standard Press of China, 2019.
[29]周涵, 牟龙华, 郭文明. 基于故障分量的孤岛微电网保护[J]. 电工技术学报, 2017, 32(17): 11-20.
ZHOU Han, MU Longhua, GUO Wenming. Islanded microgrid protection based on fault components[J]. Transactions of China Electrotechnical Society, 2017, 32(17): 11-20.
Backup protection scheme based on system voltage distribution using curve fitting
SONG Guobing1, 2, CHANG Nana1, 2, HOU Junjie1, 2, CHANG Zhongxue1, 2, ZHENG Yuping3, 4, WU Tonghua3, 4
(1. School of Electrical Engineering, Xi'an Jiaotong University, Xi'an 710049, China; 2. State Key Laboratory of Electrical Insulation and Power Equipment (Xi'an Jiaotong University), Xi'an 710049, China; 3. NARI Group (State Grid Electric Power Research Institute)Corporation, Nanjing 211106, China; 4. State Key Laboratory of Smart Grid Protection and Control, Nanjing 211106, China)
The diversity of topologies and the complexity of power supply characteristics make the setting workload of backup protection based on steady-state current large and a mismatch occurs from time to time. Backup protection technology without setting and with an automatic coordination function is the goal of relay protection workers. Based on the analysis of the problems of traditional inverse-time overcurrent (ITOC) protection and the distribution characteristics of positive and negative sequence voltage fault components in a radial distribution network, a backup protection scheme using curve fitting based on system voltage distribution is proposed. The proposed scheme uses the system distribution of compound voltage sequence components and the minimum action time of step-by-step coordination between all protections to fit the action curve with inverse-time characteristics, and obtains the fitted piece-wise function expression. The calculated protection action time can automatically reflect the topological relationship between each protection and fault location, and realize the adaptive coordination of all protections and meet the requirements of selectivity and rapidity. DG access does not change the distribution characteristics of the compound voltage sequence component, so the proposed method is adaptive to the network with DG. Theoretical analysis and simulation results show that the proposed method can automatically realize the fast and step-by-step coordination of upstream and downstream protections in the case of any point fault.
backup protection; compound voltage sequence component; curve fitting; adaptive coordination; DG access
10.19783/j.cnki.pspc.211394
国家电网有限公司科技项目资助(5100- 202040327A-0-0-00)
2021-10-05;
2021-11-16
宋国兵(1972—),男,博士,教授,博士生导师,研究方向为电力系统继电保护;E-mail: song.gb@163.com
常娜娜(1991—),女,通信作者,博士研究生,研究方向为电力系统继电保护;E-mail: 496296983@qq.com
侯俊杰(1993—),男,博士研究生,研究方向为电力系统继电保护。E-mail: 826686025@qq.com
This work is supported by the Science and Technology of State Grid Corporation of China (No. 5100-202040327A-0-0-00).
(编辑 姜新丽)
