基于需求侧响应的主动配电网双层优化方法
2022-09-02王维庆王海云
陈 倩,王维庆,王海云
基于需求侧响应的主动配电网双层优化方法
陈 倩,王维庆,王海云
(新疆大学可再生能源发电与并网技术教育部工程研究中心,新疆 乌鲁木齐 830047)
分布式电源在配电网中渗透率越来越高,导致配电网电压越限问题凸显,对此构建协同考虑主动配电网设备规划和运行的双层优化模型。上层模型考虑配电网中分布式电源、静止无功补偿器及电容器组的容量配置优化以减少配电网投资运行成本。下层模型考虑需求侧响应,有载调压变压器、储能及分布式电源等设备的协调控制,着重提高电压稳定性。针对模型特征,采用基于改进麻雀算法和二阶锥规划的混合优化算法进行求解。外部采用改进麻雀算法求解多维变量以提高求解速度,内部基于二阶锥规划求得配电网主动管理控制策略。最后采用改进的IEEE33节点系统进行仿真验证。结果表明,所提出双层优化方法可以有效提高配电网运行经济性,改善配电网电压分布,平抑负荷峰谷差。
分布式发电;无功优化;主动配电网;需求侧响应;双层模型
0 引言
近年来,在低碳经济目标的影响下大量分布式可再生能源接入配电网[1],高比例风电和光伏接入配电网会加剧节点电压波动,使配电网面临电压越限的风险[2],另外配电网中分布式电源(Distributed Generation, DG)、静止无功补偿器(Static Var Compensator, SVC)及电容器组(Capacitor Bank, CB)的容量和位置对配电网的性能有很大的影响,分布式能源和无功补偿设备的最佳放置是配电网中的一个重要问题[3]。因此,对配电网进行规划和运行协同优化研究具有重要意义。
配电网中无功优化可有效减少配电网的网损并改善电压分布[3],文献[4]研究分布式电源的无功补偿能力,充分探究含分布式电源的配电网电压稳定性控制策略,文献[5]兼顾配电网中DG和无功补偿设备的协同补偿能力,采用分布式控制方法对DG和无功补偿设备进行分组控制。文献[6]建立了DG在配电网的多周期反应协调最优运行模型,考虑了两种典型风机的有功-无功协调特性,并整合了无功补偿资源的运行策略。另外,DG和无功补偿设备的位置容量配置对配电网无功优化有较大的影响,在确定SVC和CB的候选安装节点及容量的情况下建模,优化结果具有很大的人为因素,将不是主动配电网期望的优化配置方案。对此,文献[7]构建配电网规划和运行双层协调优化模型,上层决策变量为无功补偿设备安装位置和容量,下层模型决策变量为无功优化方案,以综合提高配电网运行性能。文献[8]构建以投资成本、网损和电压偏移最小为目标的配电网无功补偿装置双层优化模型,投资层和运行层协同优化共同提高配电网运行经济性和安全性。文献[9]以风电场为研究对象,构建双层模型,上层模型以年综合费用最小为目标,下层模型进行动态无功优化,保证配电网运行经济性和可靠性。除了对配电网进行无功设备优化配置和无功补偿外,为进一步保证配电网电压稳定并有效降低配电网网损,充分发挥配电网各类电压调控手段的优势,近年来,需求侧响应(Demand Response, DR)技术和储能(Energy Storage, ES)充放电功率调控也取得快速的发展。文献[10]在微电网下通过引入需求侧响应优化用户用电模式,改善负荷曲线,提高系统的稳定性。文献[11]研究需求侧响应的分时电价策略对不同时段实现不同激励以改善负荷特性。文献[12]在负荷侧调用不同响应类型和时间尺度的需求侧响应资源,与源侧协同优化降低系统的碳排放。文献[13]构建含电价刺激的需求侧响应配电网优化模型,兼顾储能设备的充放电约束,综合提高分布式电源的消纳能力,优化负荷特性。对此,针对含分布式能源的配电网如何充分发挥各无功补偿设备和需求侧响应技术的协同优化问题具有重要研究价值。
此外,兼顾配电网多种协同优化技术的模型通常具有复杂的耦合关系,难以求解。文献[14]构建含DG、有载调压变压器(On-Load Tap Changer, OLTC)和交直流换流器等的二阶锥(Second-Order Cone, SOC)规划模型,采用求解器进行求解。文献[15]基于二阶锥(SOC)松弛的交流最优潮流对主动配电网的最优运行问题进行建模求解。文献[16]则通过二阶锥松弛研究有源配电网的最优潮流。大多考虑配电网优化的模型都采用数学方法将复杂的原始模型转化为二阶锥形式求解,实际上配电网优化配置模型约束处理并不复杂,采用启发式算法可快速求解,大量文献采用启发式算法对DG或无功补偿设备进行优化配置[7,9,17]。目前,针对配电网双层优化模型采用启发式算法和二阶锥规划的混合优化算法对其进行求解的研究还不多。
综上分析,本文构建配电网规划和运行的双层优化模型,对配电网实现多点控制并实施DR策略,在增加经济性的同时改善负荷曲线和电压分布。针对模型特征,采用改进麻雀算法求解上层模型,下层模型基于二阶锥规划,在配电网多设备优化配置下实施无功优化,最终求得配电网最优配置和主动管理策略。
1 双层模型框架
配电网优化运行问题中除常规无功优化外,DG、SVC和CB的容量大小及其安装位置也是优化配置中需要解决的问题,其相互之间具有一定的制约关系。实际上SVC、CB 和DG的投资成本及维护成本各不相同,在配电网无功优化过程中配置容量和动作优先顺序会有差异。本文在主动配电网多设备规划的基础上进行配电网动态无功优化,构建主动配电网双层优化模型。
上层规划模型以DG配置容量以及CB和SVC的位置和容量为决策变量,各设备投资维护成本以及运行成本最小为目标,将所得的各设备配置容量作为约束输入下层模型。下层模型在此约束下对兼顾用户需求侧响应的主动配电网中各设备进行协调控制,保证配电网运行的电压稳定性,将下层模型求出的结果反馈给上层模型,计算运行成本,上下两层相互影响获得最终方案,双层模型为
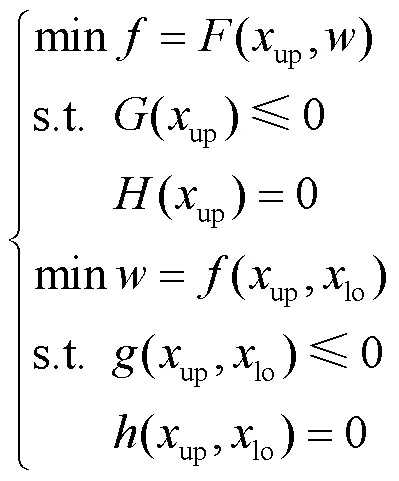
式中:为上层模型优化目标函数;和分别为上层模型不等式约束条件和等式约束条件;为下层模型优化目标函数;和分别为下层模型不等式约束条件和等式约束条件;w为上层模型目标值;和分别为上下层模型决策变量。具体优化模型如图1所示。
2 数学模型
2.1 上层模型
配电网中,OLTC一般装在首端,CB和SVC可以装在配电网的多个位置,容量也可以各不相同,需要在更大范围内进行搜索和优化。上层模型以提高配电网规划运行的经济性为目标,考虑DG、CB和SVC投资维护成本,折算到以年为单位,另外配电网运行过程中的网络损耗属于系统运行技术指标,将其转化为经济性衡量[7],构建配电网上层规划模型。
2.1.1上层模型目标函数
DG投资维护成本DGc为
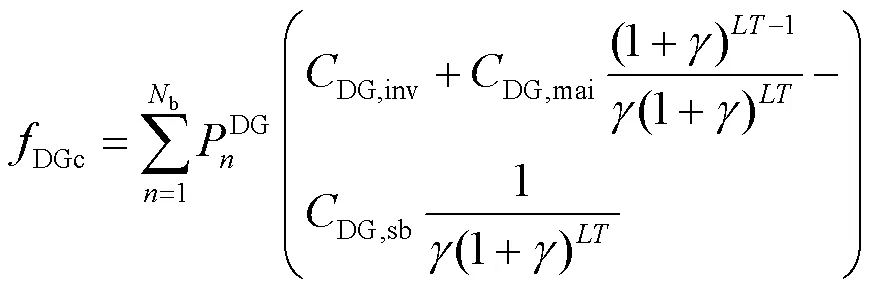
CB投资维护成本CBc为
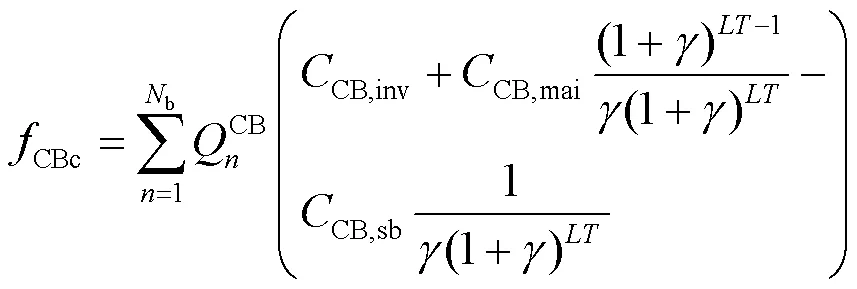

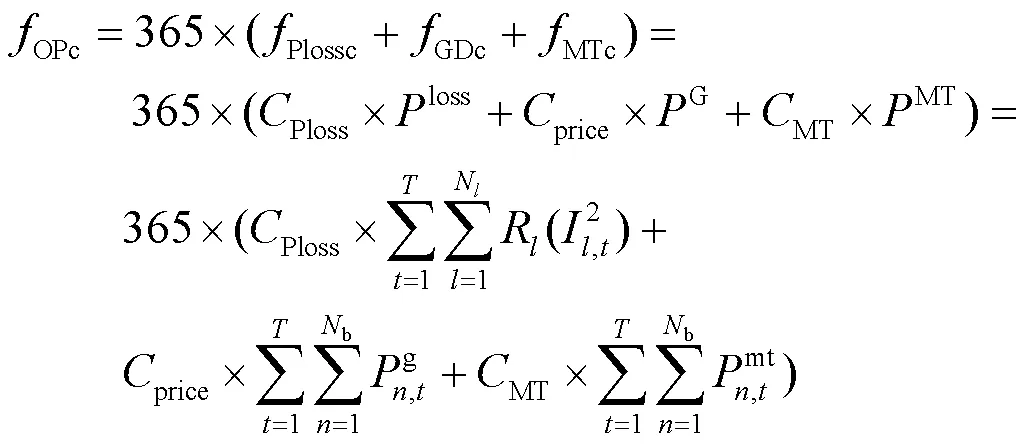
上层模型目标为
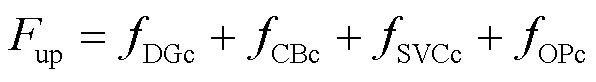
2.1.2 上层模型约束条件
配电网进行规划时受到建设地点和资金的限制,不同节点装设设备的数量和容量会受到制约,约束条件如下所述。
1) DG容量约束

2) CB容量约束
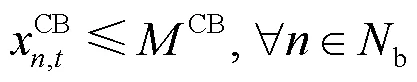
3) SVC容量约束
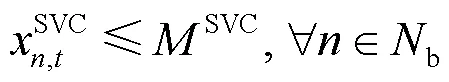
2.2 下层模型
下层模型充分考虑在价格激励下负荷的灵活性,用户根据电价信号做出响应改变用电策略,在尽量不减少用户体验的情况下节省用电成本,提高了配电网电压稳定性。
2.2.1需求侧响应
主要考虑受分时电价影响的需求侧响应,负荷转移量与不同时段的电价有关,用户参考不同时段的电价调整用电习惯改善负荷曲线。需求侧响应中可转移负荷在一定范围内变化并且保证一天内整体变化负荷量维持在一定小范围内,其约束为
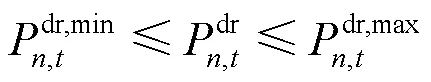
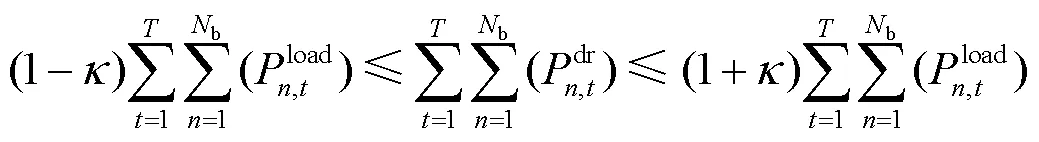
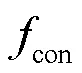
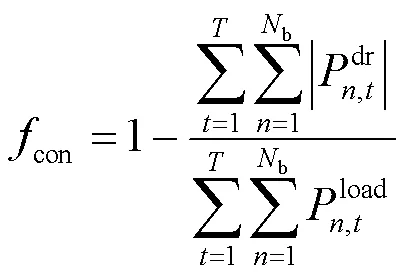
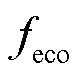

2.2.2下层模型目标函数
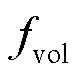
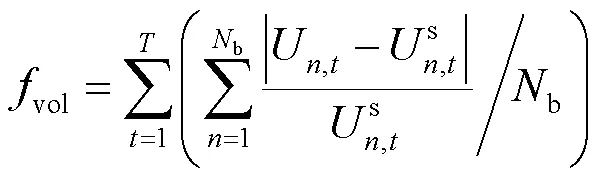
下层目标函数为

2.2.3下层模型约束条件
下文中下标均表示设备台数。
2.2.3.1 DR约束
如式(10)和式(11)所示。
2.2.3.2 ES约束
1) 充放电状态约束
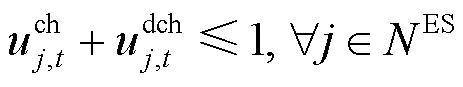
2) 功率约束
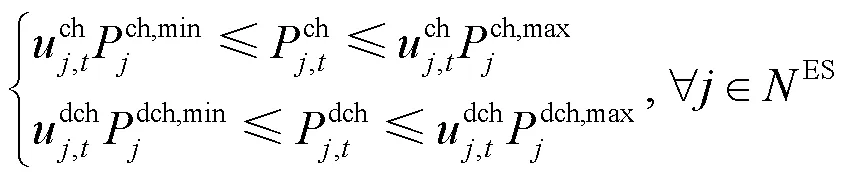
3) 容量约束
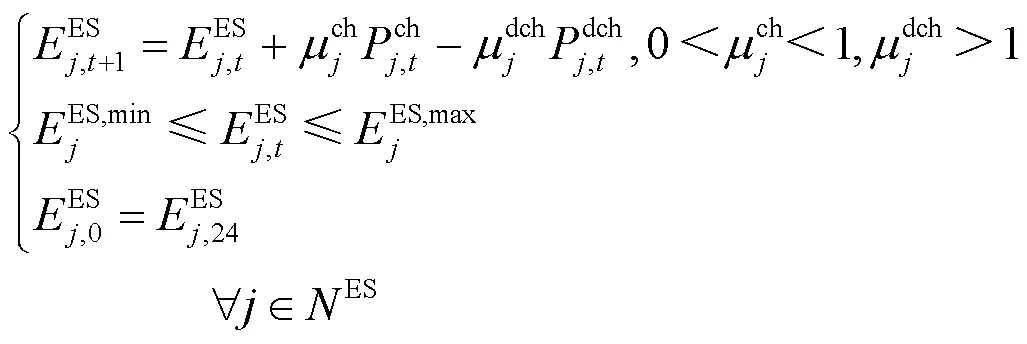
2.2.3.3 DG约束
1) 风机约束
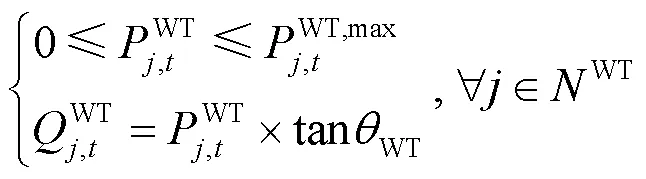
2) 光伏约束
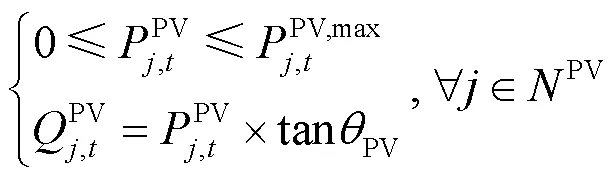
3) 燃气轮机约束

2.2.3.4 SVC约束
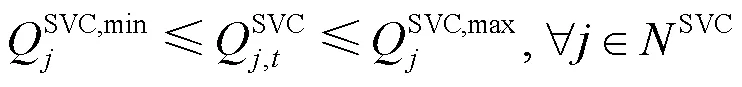
2.2.3.5 CB约束
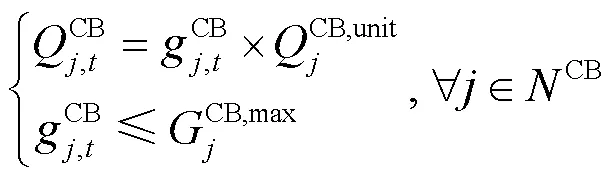
一般情况下电容器组投切次数具有一定限制,构建约束条件为
2.2.3.6 OLTC约束
通过对有载调压变压器变比的改变调节配电网变电站母线节点电压,改善配电网整体电压分布情况[18],有载调压变压器变比和母线节点电压之间的约束为
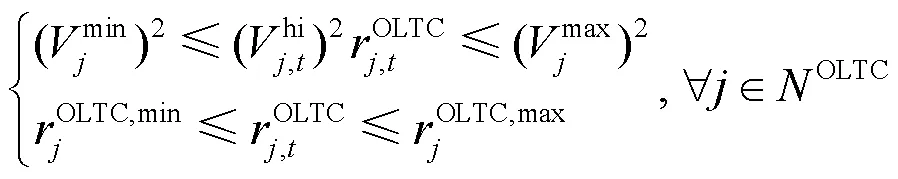
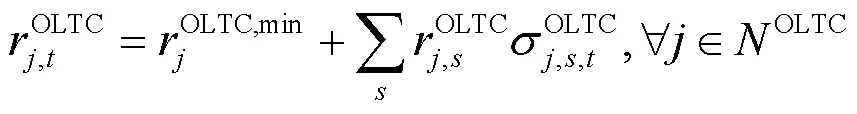
一般情况下有载调压变压器变比变化次数也具有一定限制,构建约束条件为
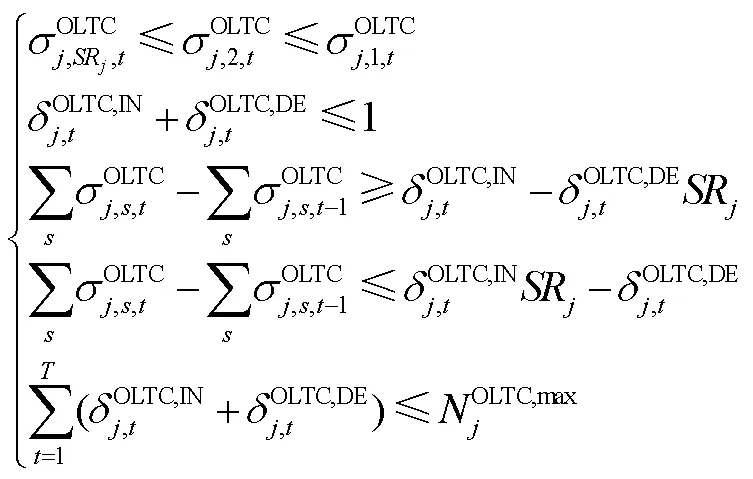
2.2.3.7发电机功率约束

2.2.3.8潮流约束
辐射状配电网如图2所示。
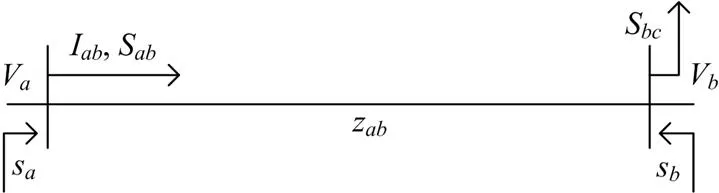
图2 辐射状配电网示意图
其潮流方程为
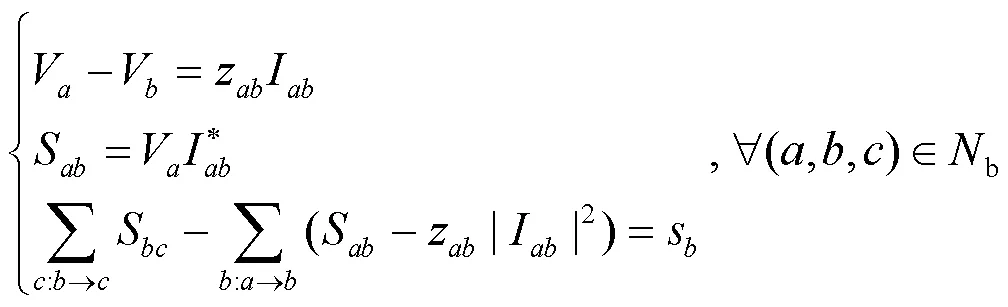
2.2.3.9节点电压约束
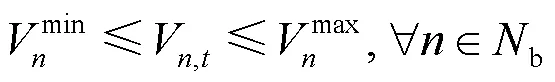
2.2.3.10支路电流约束
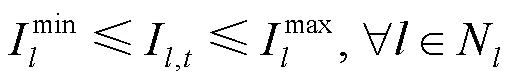
3 混合优化算法
配电网双层优化问题属于大规模优化问题,难以保证求解精度和速度之间的平衡,而本文在配电网双层优化的基础上进一步考虑了储能设备充放电功率约束和需求侧响应,这使得原问题变得更加复杂,对此提出基于改进麻雀算法和混合整数二阶锥规划的混合优化算法对本文问题进行求解,将大规模高维度的原问题转化为配电网规划和无功优化分开求解的子问题,上层采用改进麻雀算法求解,下层将无功优化问题转化为混合整数二阶锥规划问题,通过Yalmip调用CPLEX进行求解。
3.1 改进麻雀算法
麻雀算法[19]搜索精度高,收敛速度快,稳定性好,鲁棒性强,但也无法避免在接近全局最优解时,样本多样性减少易陷入局部最优的问题。对此,首先利用混沌变量初始化种群增加多样性,本文采用Tent映射进行种群初始化,其数学表达式为
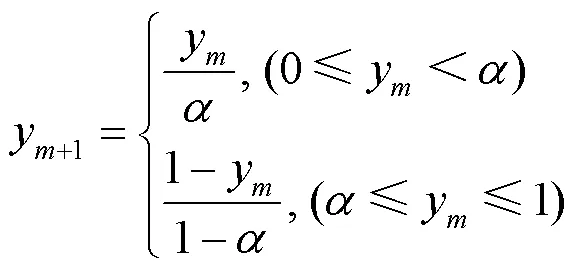
本文取,Tent混沌序列分布图如图3所示,可知Tent映射均匀性较好。
混沌扰动的步骤描述如下所述。
2) 将混沌变量变换到待求解问题的解空间。

3) 按式(34)对个体进行混沌扰动。

然后增加“Levy飞行”策略并兼顾近处和远处的距离增加搜索范围,Levy飞行的连续跳跃路径与时间服从Levy分布,对其简化并进行傅里叶变换,得到其幂次形式的概率密度函数。
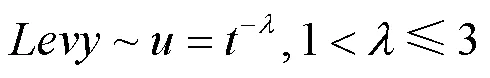
式中,是幂次数。式(35)是一个带有重尾的概率分布,但通过较为简单的程序语言实现比较困难,因此当计算Levy飞行的搜索路径()时,通常采用Mantegna提出的模拟Levy飞行路径的计算公式,如式(36)所示。

式中:即为 Levy飞行路径();参数的取值为0<< 2,本文取= 1.5;参数、为正态分布随机数,服从式(37)的正态分布。
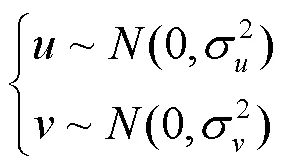

在加入Levy飞行策略后,加入者按式(39)进行位置更新。

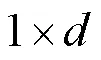
在原始麻雀算法中,加入混沌策略初始化种群,引入Levy飞行中的随机步长使得麻雀种群中加入者的搜索方向和步长变得不确定,大小范围交替搜索,增加种群位置的多样性,提高算法跳出局部最优解的能力。
改进麻雀算法步骤如下:
1) 输入迭代次数以及初始的捕食者和加入者比列,再利用Tent映射策略初始化种群;
2) 计算适应度值并排序;
3) 更新麻雀种群中捕食者位置;
4) 更新麻雀种群中加入者位置;
5) 更新麻雀种群中警戒者位置;
7) 满足停止条件,则退出,输出结果;否则,重复执行步骤2)至步骤6)。
3.2 模型转化
根据所建模型特征进行转换,将原混合整数非凸非线性问题转化为混合整数二阶锥规划问题,具体转化过程如下所示。
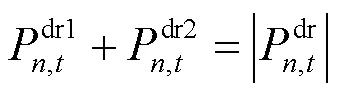
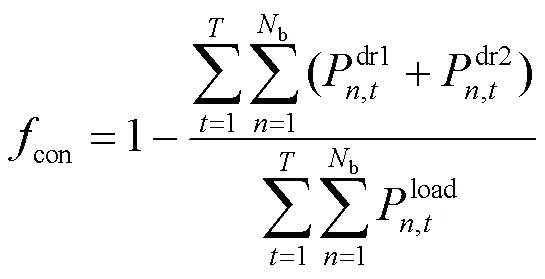
增加约束:
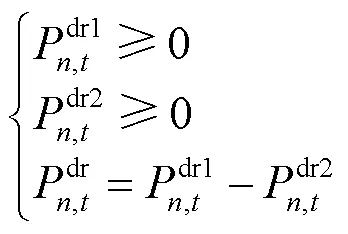

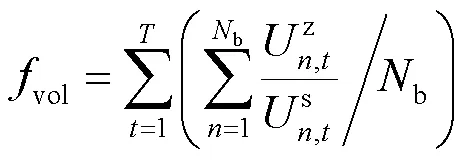
增加约束:
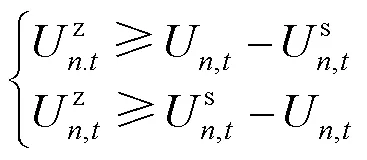
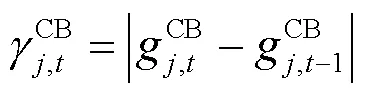

增加约束:
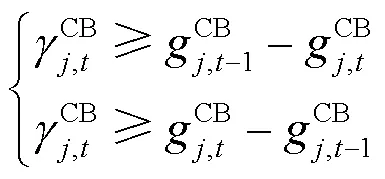
进一步进行缩放转化:
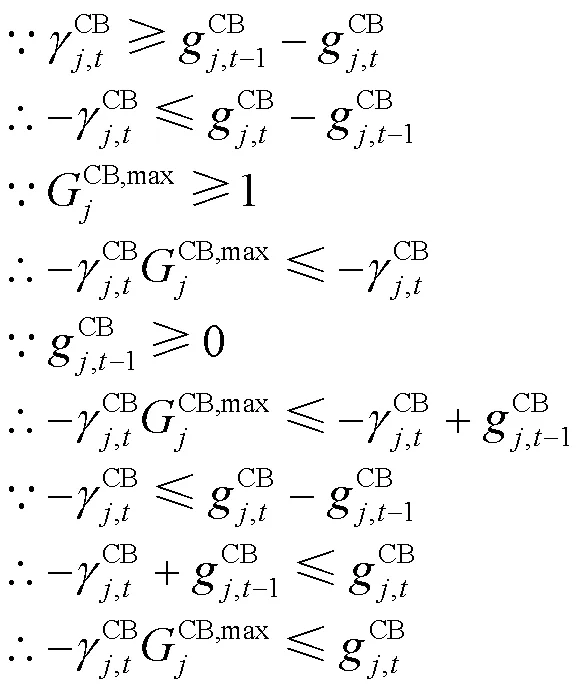
综上所述,进行类比整理得CB投切次数约束:
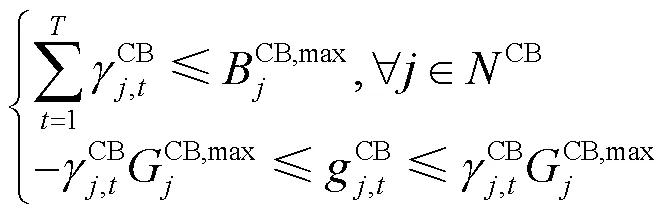

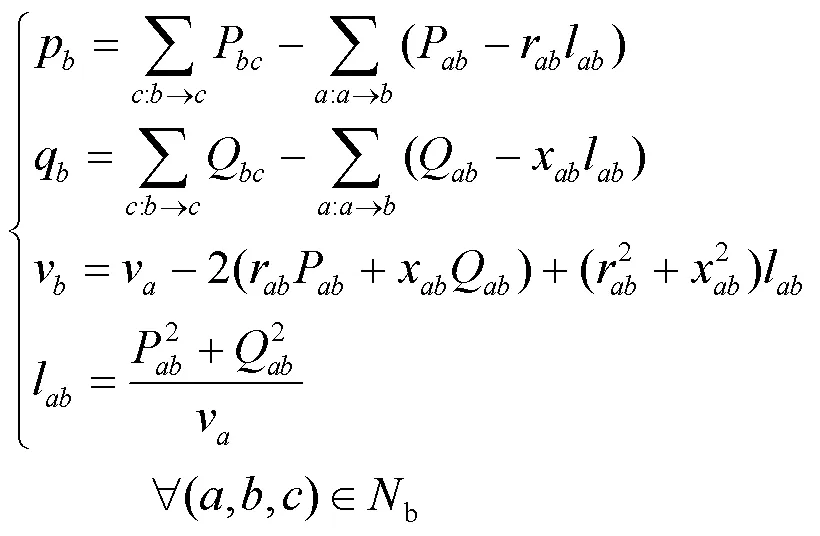
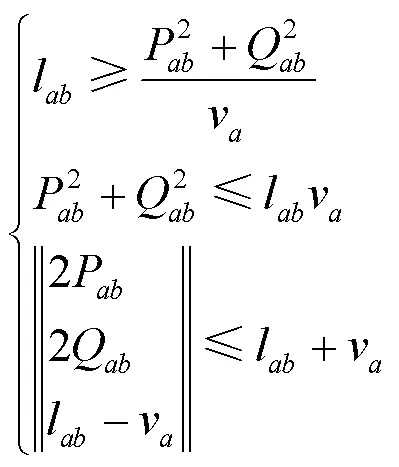
考虑本文可调控手段和设备出力调度,辐射状配电网示意图如图4所示。
综合潮流约束,得
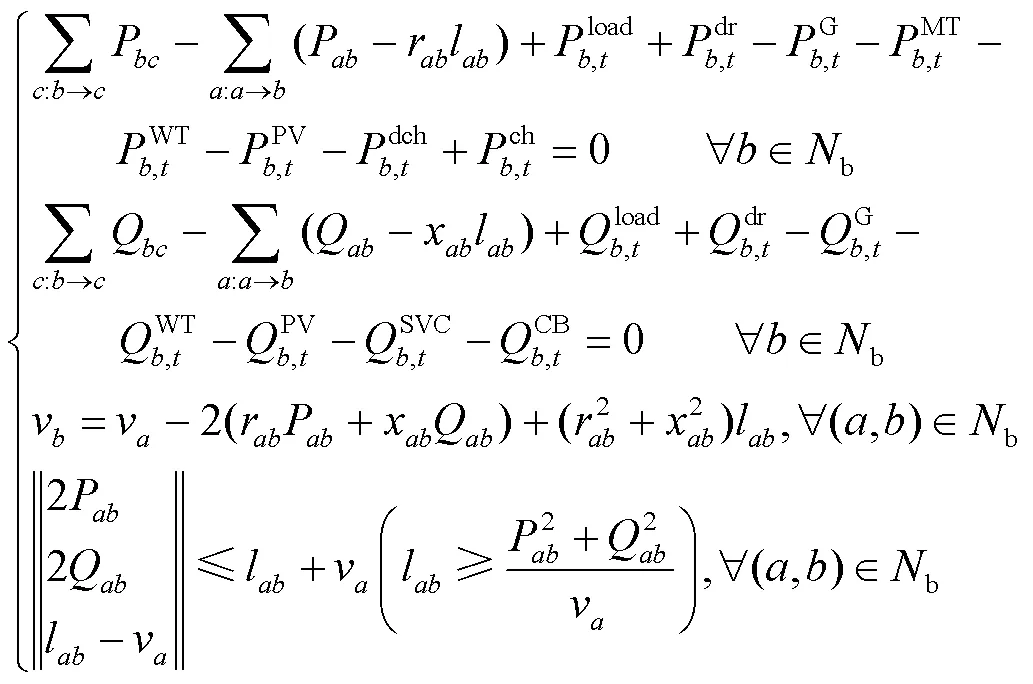
针对上述混合整数二阶锥规划问题,采用Cplex算法包进行求解。
3.3 算法流程
针对基于需求侧响应的配电网双层优化模型,采用混合优化算法进行求解,流程图如5所示。
4 仿真分析
为了验证本文考虑需求侧响应的配电网双层优化策略和算法的有效性,以IEEE33节点系统为例,基于Matlab2016a的运行环境进行编程仿真。配电网中OLTC一般装在首端,文献[8]研究了OLTC多目标优化配置,参考此文献,本文在IEEE33节点系统首端有OLTC,调节范围为[0.94, 1.06],其余待优化变量的具体参数如表1所示,风机,燃气轮机,光伏的投资成本不同,具体参数见文献[17, 20],系统其他参数参考文献[7, 21-22],下层目标权值相等。设置改进麻雀算法种群规模= 50,最大迭代次数= 200,麻雀算法预警值= 0.6,发现者的比例= 0.7,剩下的麻雀为加入者,意识到有危险的麻雀比重= 0.2,配电网典型日内负荷曲线和配电网交易电价[21]如图6和图7所示。
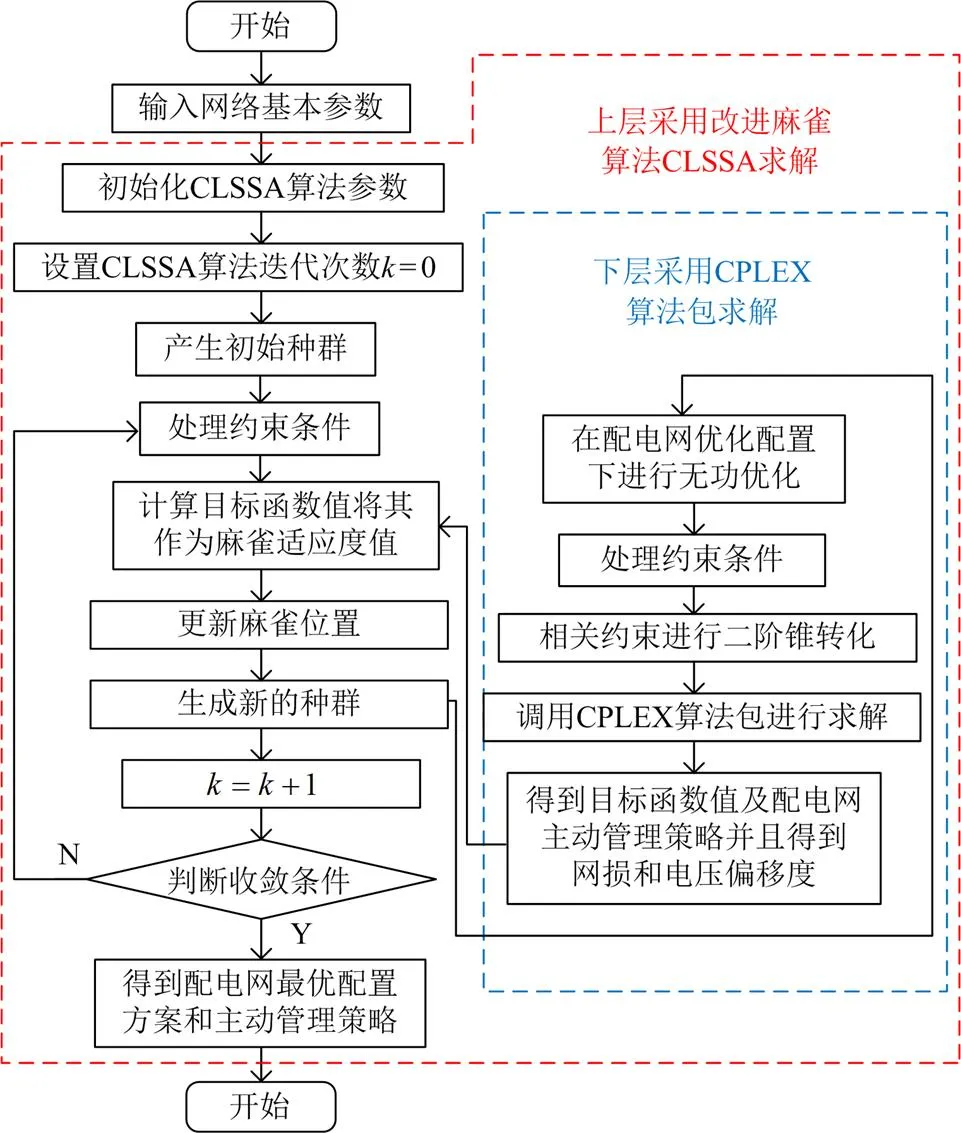
图5 混合优化算法流程图
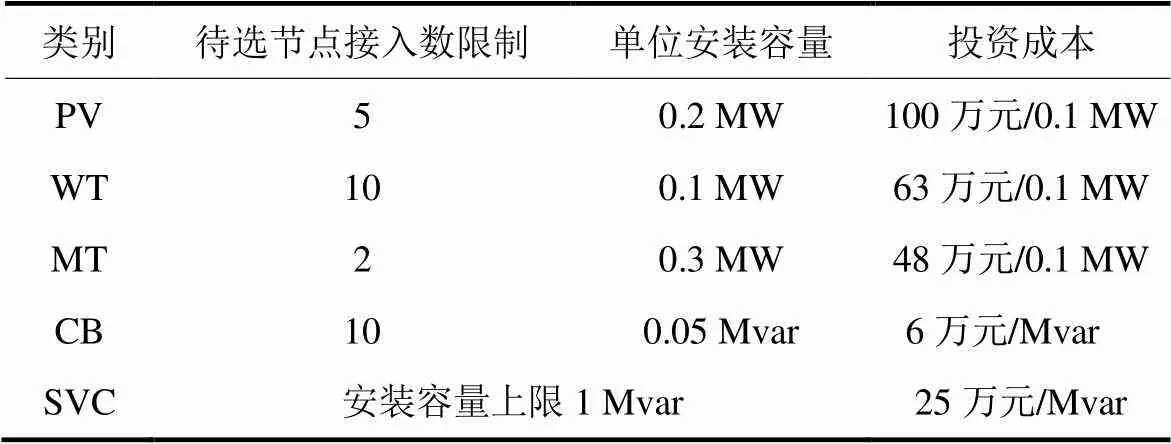
表1 待优化变量的具体参数
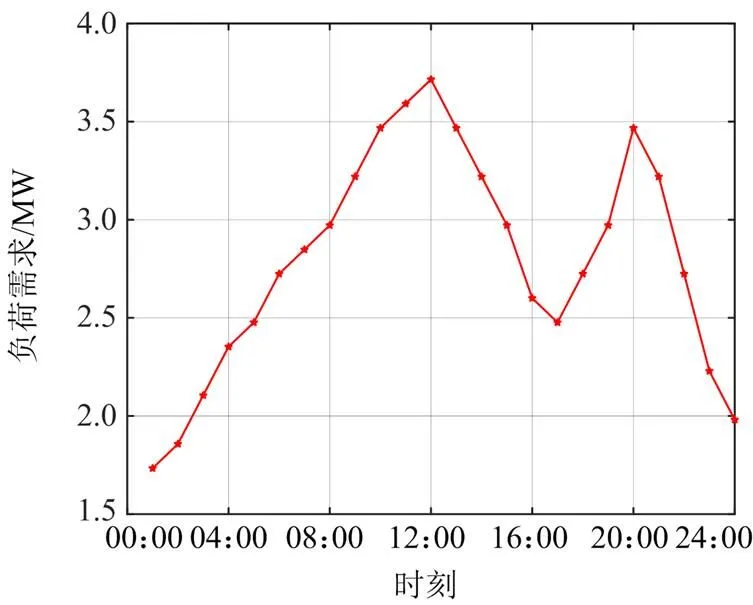
图6 负荷曲线

图7 配电网交易电价
4.1 不同优化模型对比
本节主要分析配电网中单层模型(固定配置模型)和双层模型对配电网投资运行成本和电压偏移的影响,分别采取本文算法在仅无功优化和本文双层模型的情况下对比分析,不同优化模型下的优化配置结果如表2所示。

表2 优化配置结果
由表2可知,本文模型DG配置容量上整体少于固定配置,无功补偿设备的配置容量高于固定配置,这是由于DG投资成本高于无功补偿设备,在不考虑DG消纳问题时,适当增加配电网中无功补偿设备可以保证配电网经济安全运行,具体投资运行费用如表3所示。
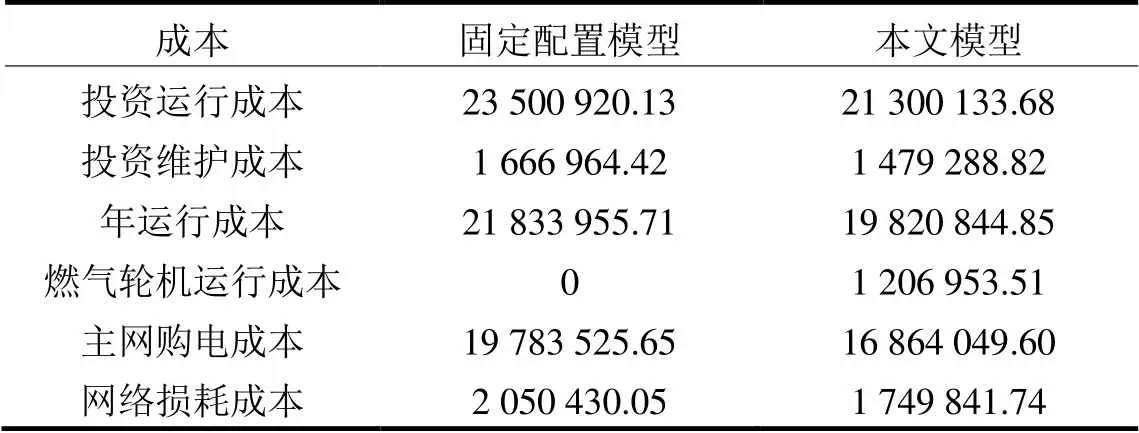
表3 不同优化模型的目标结果
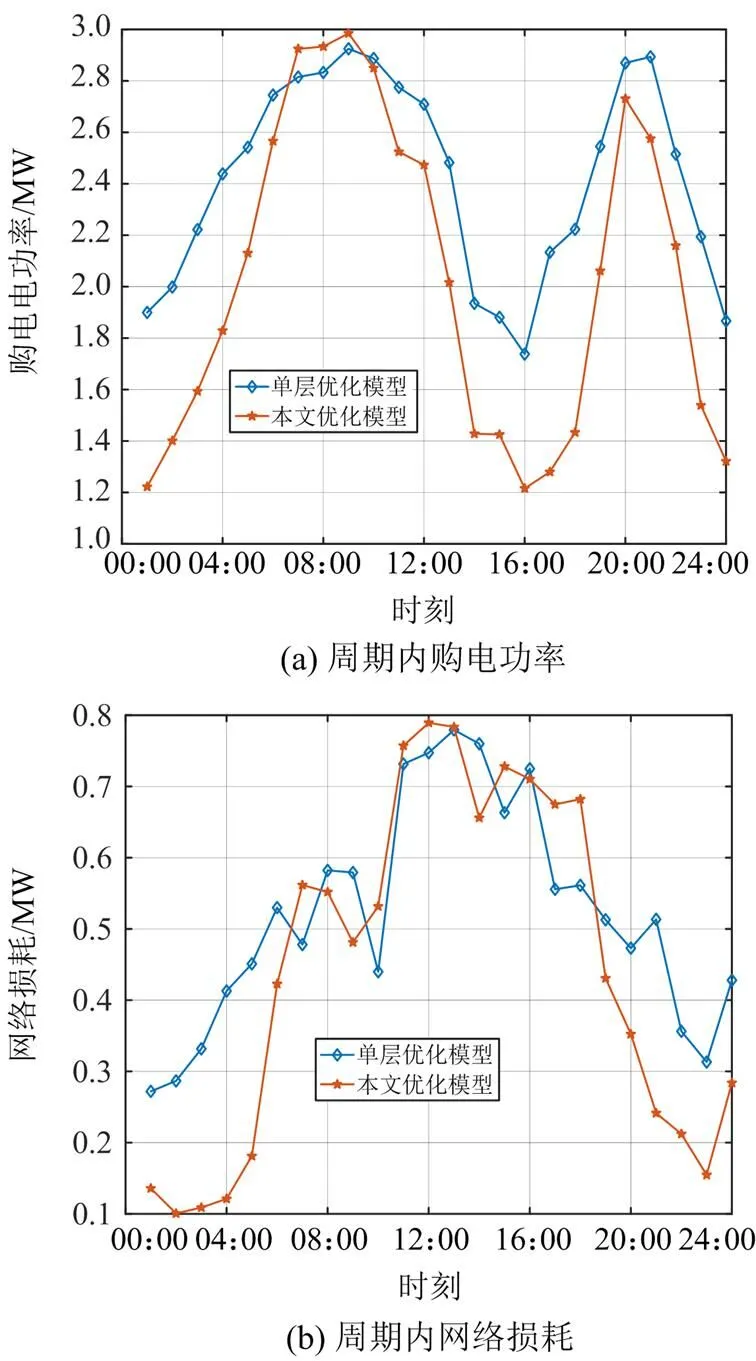
由表3可知,本文模型的投资运行费用整体少于固定配置,并且投资维护费用和年运行费用都少于固定配置下的成本。对年运行成本具体分析,本文模型配置有燃气轮机,虽然其发电会消耗一定费用,但其发电会减少配电网向主网的购电量,整体上本文优化配置下的运行成本更少,主网购电成本和网络损耗成本都较小,这表明本文优化模型具有更高的经济性,并且验证了对含DG的配电网进行主动控制管理时先优化系统各设备配置方案的必要性。不同模型下周期内优化结果对比如图8所示。
图8显示几乎所有时段内本文优化模型下的周期内购电电功率、网络损耗和电压偏差都较小,整体上与固定配置下的优化模型差距较大,具有显著的优势,表明本文模型可以在减少年综合运行成本情况下保证配电网更经济稳定的运行,本文双层优化模型对配电网主动控制有着积极的作用。
4.2 不同策略对比
本节主要分析配电网中实施DR和兼顾ES充放电功率约束对配电网双层优化的影响,分别采取本文算法在有无DR和ES的情况下对比分析,在不同策略下的下层模型的电压偏移度和目标值如表4所示。

表4 不同策略的结果
表4中显示无DR策略时目标值最大,这是因为没有DR策略时用户不用考虑节约用电成本,不用转移用电量,目标值后部分为0.25,目标变大,另外,无储能装置时电压偏移度和目标值也都较高,本文策略下电压偏移度和下层目标值较小,从侧面表明DR策略和兼顾ES充放电功率约束可以在一定程度上改善配电网运行性能。本文策略在进行DR前后负荷变化如图9所示。
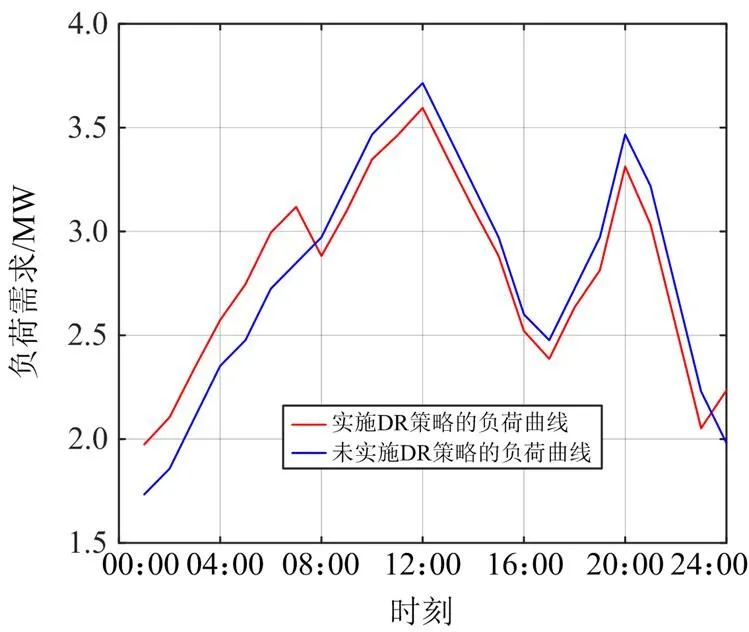
图9 实施DR前后的负荷曲线
图9红色曲线是在DR策略下的负荷曲线,在低价时段用户增加用电量,当电价较高时,负荷减少,以此说明DR策略有效地改善了负荷曲线,具有削峰填谷的作用。不同策略在周期内的电压偏差如图10所示。
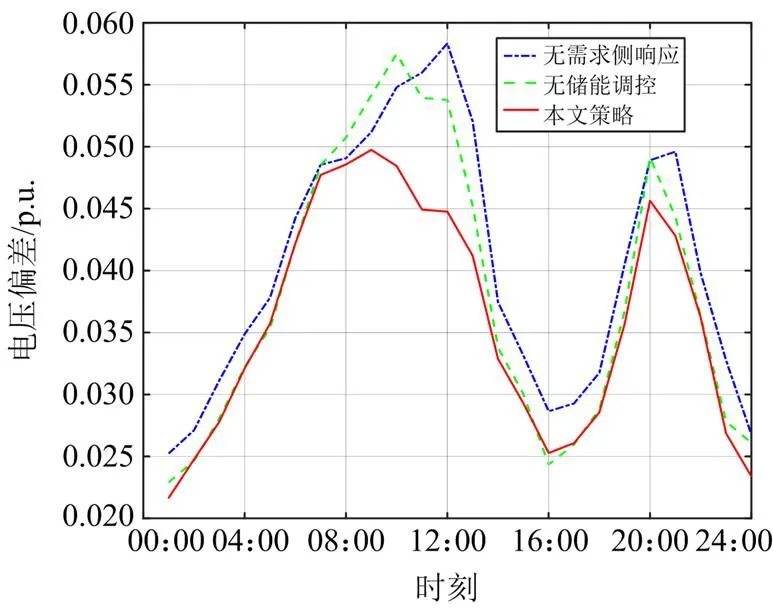
图10 不同策略周期内的电压偏差
由图10可知,几乎所有时段内本文策略的电压偏差都更小,具有一定优势,这表明在配电网中实施DR和储能调控可以有效减少电压偏差,使得电压分布更加平稳。不同策略在周期内的无功出力如图11所示。
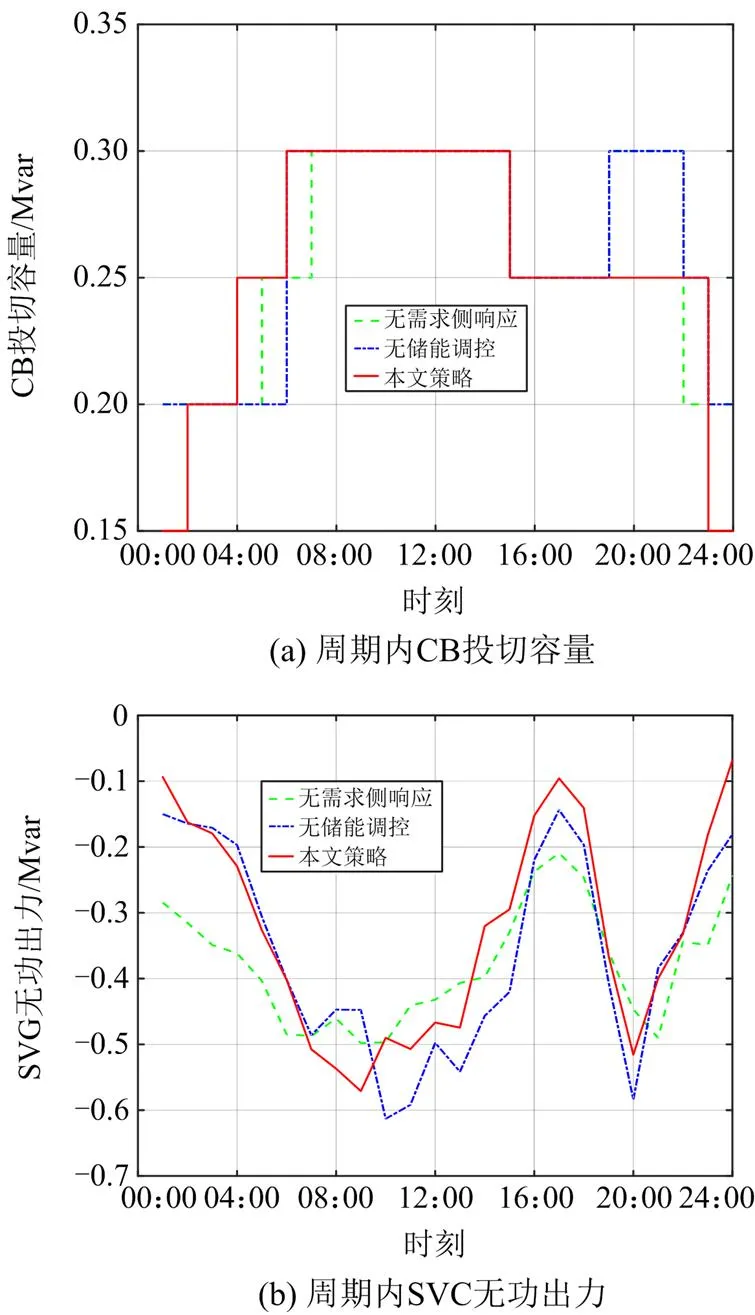
图11 不同策略周期内的无功出力
由图11可知,在配电网周期内不同策略下,本文策略的无功出力整体相对较小,可节约无功出力。另外,不同策略在周期内的DG有功出力如图12所示。
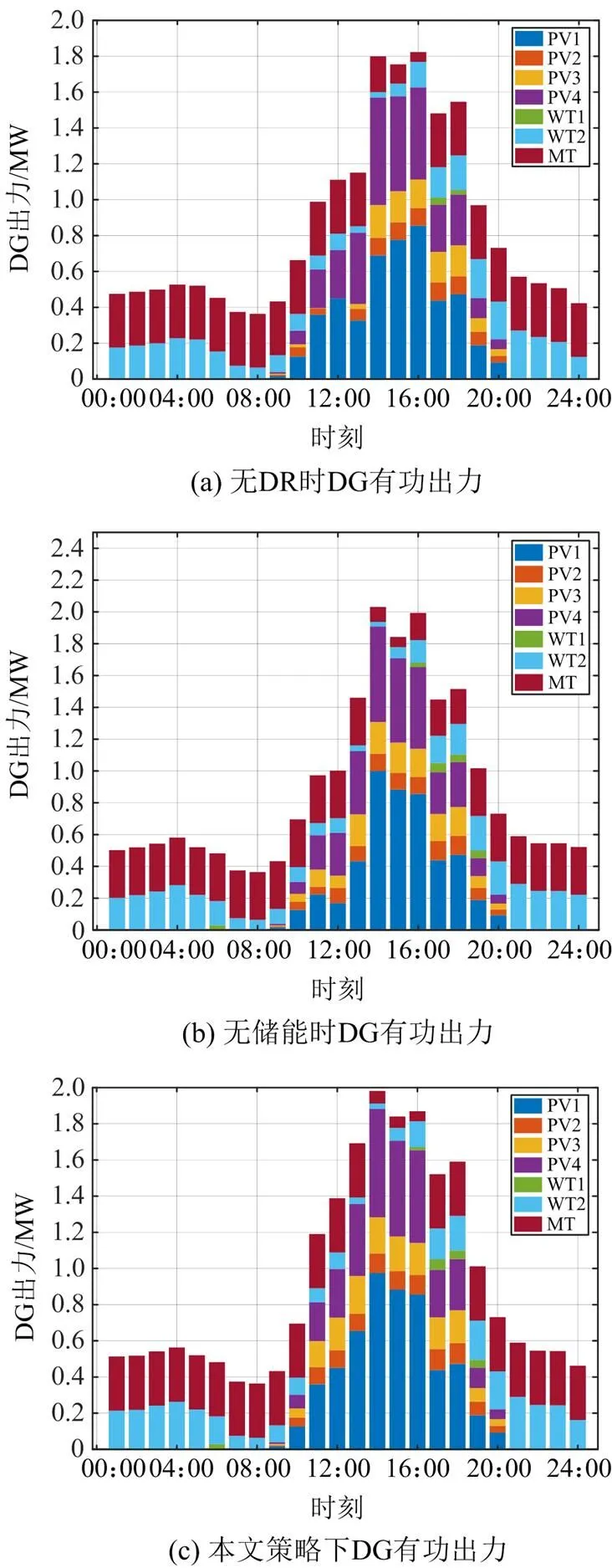
图12 多时段DG有功出力
由图12可知,整体上看DG有功出力和负荷需求的分布趋势一致,风光互补发电尽量满足负荷需求,储能调控可以在一定程度上减少DG出力波动保其平稳发电。有DR策略时,负荷特性变好,在电价便宜时段负荷量增加,同时段DG出力增加,有助于DG消纳。
4.3 不同算法对比
本节主要分析不同算法对配电网双层优化模型求解精度和速度的影响,本文分别采取粒子群算法[23]、改进麻雀算法和本文混合优化算法进行求解,不同算法求解结果如表5所示。
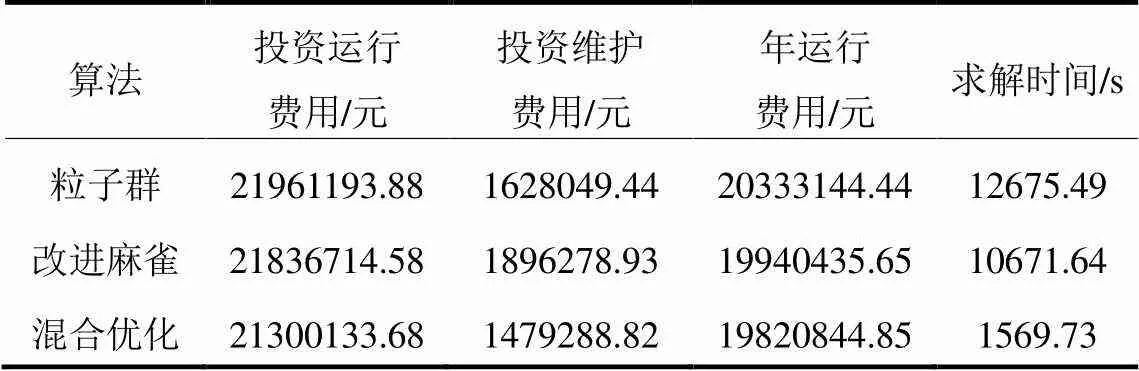
表5 不同算法求解的结果
表5中显示不同算法求解所获得的成本以及求解时间都有不同程度的差异,粒子群算法和改进麻雀算法都为启发式算法在求解大规模多约束问题时易产生大量不可行解,需进行多次迭代操作,耗费大量时间,改进麻雀算法较粒子群算法求解精度和速度有一定的提升,混合优化算法进一步缩短了求解时间,且获得解更小,具有更高的求解效率。本文的混合优化算法较其他算法在不同指标上改善的程度如图13所示。
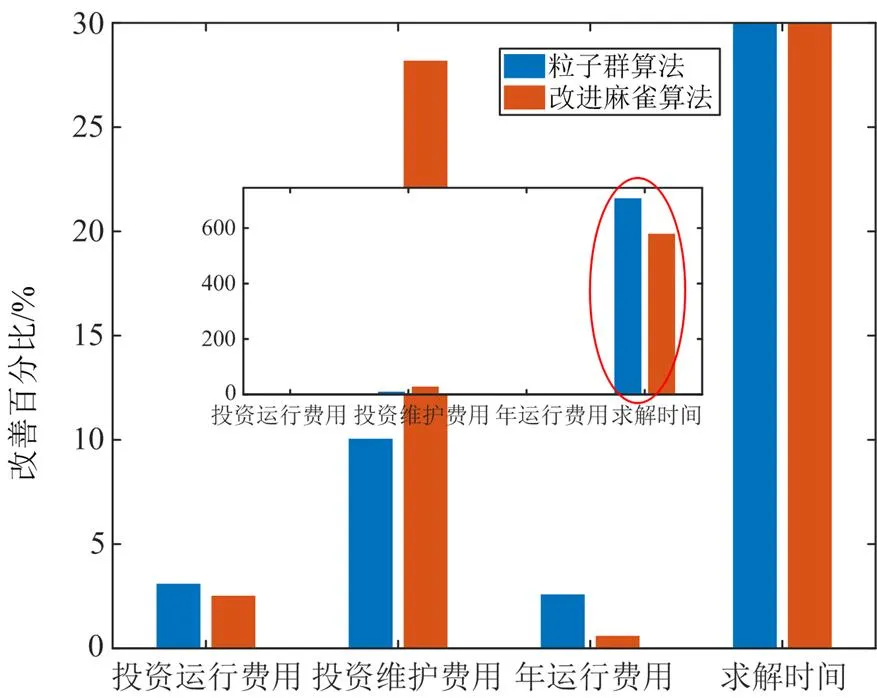
图13 本文算法较其他算法各指标改善的百分比
图13中以本文混合优化算法为基准,正数表示本文优化算法较其他算法有改善,负数表示本文优化算法较其他算法在指标上恶化了,全为正数表示本文优化算法在各个指标上都具有优势,由图13可知混合优化算法较改进麻雀算法和粒子群算法在求解速度和精度上得到进一步改善,具有显著优势。
下层模型通过权重系数将多目标优化简化成单目标优化,简化了优化算法,但是权重选取对最终的优化结果会有不同程度的影响,还需在不同权重系数的组合和取值空间内深入讨论,为验证不同权值对优化结果的影响,不同权重系数组合及其目标结果如表6所示。
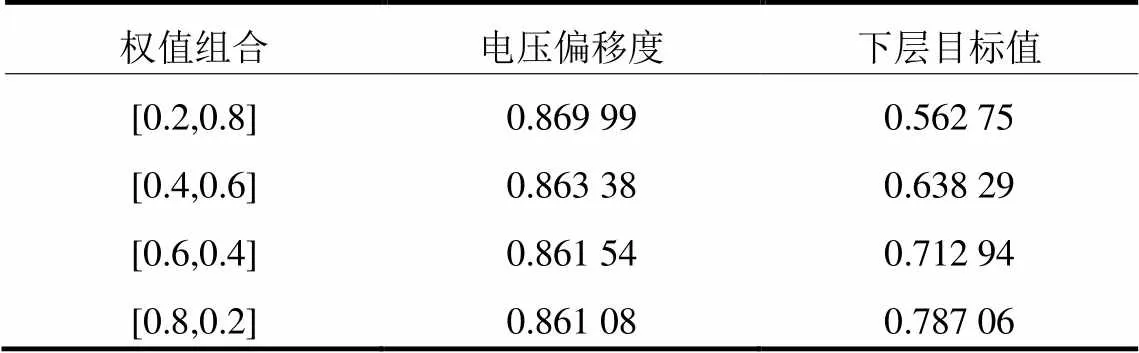
表6 不同权值下目标结果
表6中显示不同权值下电压偏移度随着其权值的增大而减小,这是由于权值越大其在目标中所占比重越大,其值优化力度越大,目标值越小越好,则权重越大目标值更小更优,而随着电压偏移度权值变大整体优化值变大,这暗示着随着关于DR策略的权值变小其值越来越大,这是由于其权值变小、优化力度变小,导致其值越来越大,两者处于矛盾状态,难以找到合适的权值使得两者都更优。不同权值下各优化目标不同,整体目标也不同,根据需要如何选取合适的目标权值是十分重要的问题。
5 结论
本文考虑需求侧响应并对含分布式能源的配电网进行双层优化,充分发挥主动配电网中各设备协同优化潜力,需求侧响应和储能充放电功率调控可以改善负荷曲线,节省用电成本,有效提高电压水平。系统各设备配置优化和无功优化对电压影响较大,并且对彼此具有积极作用,可以进行协同优化避免单一优化方式无法完全消除电压越限问题。另外,本文混合优化算法上层采用改进麻雀算法求解设备优化配置问题,下层采用混合整数二阶锥规划求解保证求解精度,大大提高了求解效率。
[1] 潘本仁, 王和春, 张妍, 等. 含分布式电源的主动配电网重构策略研究[J]. 电力系统保护与控制, 2020, 48(15): 102-107.
PAN Benren, WANG Hechun, ZHANG Yan, et al. Study on an active distribution network reconstruction strategy with distributed power supply[J]. Power System Protection and Control, 2020, 48(15): 102-107.
[2] 季玉琦, 潘超, 肖晗, 等. 分布式电源电压支撑能力层次分析评价[J]. 电力系统保护与控制, 2021, 49(11): 163-171.
JI Yuqi, PAN Chao, XIAO Han, et al. Hierarchical analysis and evaluation of the voltage support capability of distributed generation[J]. Power System Protection and Control, 2021, 49(11): 163-171.
[3] FU Xueqian. Statistical machine learning model for capacitor planning considering uncertainties in photovoltaic power[J]. Protection and Control of Modern Power Systems, 2022, 7(1): 51-63.
[4] 顾洁, 孟璐, 朱曈彤, 等. 数据驱动的无精确建模含源配电网无功运行优化[J]. 电力自动化设备, 2021, 41(1): 1-11.
GU Jie, MENG Lu, ZHU Tongtong, et al. Data-driven optimization for reactive power operation in source distribution network without accurate modeling[J]. Electric Power Automation Equipment, 2021, 41(1): 1-11.
[5] 乐健, 周谦, 王曹, 等. 无功补偿设备和分布式电源协同的配电网优化控制策略研究[J]. 电力系统保护与控制, 2020, 48(18): 38-47.
LE Jian, ZHOU Qian, WANG Cao, et al. Research on distributed optimal control strategy for a distribution network based on the cooperation of DGs and Var compensators[J]. Power System Protection and Control, 2020, 48(18): 38-47.
[6] XIANG Yue, ZHOU Lili, HUANG Yuan, et al. Reactive coordinated optimal operation of distributed wind generation[J]. Energy, 2021, 218.
[7] 朱曈彤, 顾洁, 金之俭, 等. 规划与运行融合的配电网无功补偿智能协调配置[J]. 电力自动化设备, 2019, 39(2): 36-43.
ZHU Tongtong, GU Jie, JIN Zhijian, et al. Intelligent harmonious collocation for reactive power compensation of distribution network combining planning and operation[J]. Electric Power Automation Equipment, 2019, 39(2): 36-43.
[8] 田宇, 黄婧, 谢枭, 等. 主动配电网无功补偿和OLTC鲁棒多目标优化配置[J/OL]. 中国电力: 1-13[2021-12-28]. http://kns.cnki.net/kcms/detail/11.3265.TM.20210707.1646.002.html.
TIAN Yu, HUANG Jing, XIE Xiao, et al. Multi-objective optimal allocation of reactive compensation and OLTC in active distribution network[J/OL]. Electric Power: 1-13[2021-12-28]. http://kns.cnki.net/kcms/detail/11.3265. TM.20210707.1646.002.html.
[9] 黄震希, 张祥龙, 刘燕华, 等. 基于风电功率变化典型场景的风电场无功补偿优化配置[J]. 电力系统保护与控制, 2018, 46(3): 51-60.
HUANG Zhenxi, ZHANG Xianglong, LIU Yanhua, et al. Optimal configuration of wind farm reactive power compensation based on wind power fluctuation typical scenarios[J]. Power System Protection and Control, 2018, 46(3): 51-60.
[10] 赵波, 汪湘晋, 张雪松, 等. 考虑需求侧响应及不确定性的微电网双层优化配置方法[J]. 电工技术学报, 2018, 33(14): 3284-3295.
ZHAO Bo, WANG Xiangjin, ZHANG Xuesong, et al. Two-layer method of microgrid optimal sizing considering demand-side response and uncertainties[J]. Transactions of China Electrotechnical Society, 2018, 33(14): 3284-3295.
[11] 刘浩田, 陈锦, 朱熹, 等. 一种基于价格弹性矩阵的居民峰谷分时电价激励策略[J]. 电力系统保护与控制, 2021, 49(5): 116-123.
LIU Haotian, CHEN Jin, ZHU Xi, et al. An incentive strategy of residential peak-valley price based on price elasticity matrix of demand[J]. Power System Protection and Control, 2021, 49(5): 116-123.
[12] 崔杨, 邓贵波, 曾鹏, 等. 计及碳捕集电厂低碳特性的含风电电力系统源-荷多时间尺度调度方法[J/OL]. 中国电机工程学报: 1-18[2021-12-28].https://doi.org/10. 13334/j.0258-8013.pcsee.210697.
CUI Yang, DENG Guibo, ZENG Peng, et al. Multi-time scale source-load dispatch method of power system with wind power considering low-carbon characteristics of carbon capture power plant[J/OL]. Proceedings of the CSEE: 1-18 [2021-12-28]. https://doi.org/10.13334/j.0258- 8013.pcsee.210697.
[13] 张超, 左高, 腾振山, 等. 基于需求侧响应的配电网优化调度研究[J]. 智慧电力, 2020, 48(2): 53-57, 91.
ZHANG Chao, ZUO Gao, TENG Zhenshan, et al. Optimal dispatch of distribution network considering demand response[J]. Smart Power, 2020, 48(2): 53-57, 91.
[14] 巨云涛, 黄炎, 张若思. 基于二阶锥规划凸松弛的三相交直流混合主动配电网最优潮流[J]. 电工技术学报, 2021, 36(9): 1866-1875.
JU Yuntao, HUANG Yan, ZHANG Ruosi. Optimal power flow of three-phase hybrid AC-DC in active distribution network based on second order cone programming[J]. Transactions of China Electrotechnical Society, 2021, 36(9): 1866-1875.
[15] CHEN Houhe, LIU Chuqiao, FU Linbo, et al. Collaborative optimal operation of transmission system with integrated active distribution system and district heating system based on semi-definite programming relaxation method[J]. Energy, 2021, 227.
[16] LUCIEN B, ANDREAS V, SPYROS C. Second-order cone relaxations of the optimal power flow for active distribution grids: comparison of methods[J]. International Journal of Electrical Power & Energy Systems, 2021, 127.
[17] 高红均, 刘俊勇. 考虑不同类型DG和负荷建模的主动配电网协同规划[J]. 中国电机工程学报, 2016, 36(18): 4911-4922, 5115.
GAO Hongjun, LIU Junyong. Coordinated planning considering different types of DG and load in active distribution network[J]. Proceedings of the CSEE, 2016, 36(18): 4911-4922, 5115.
[18] 高红均, 刘俊勇, 沈晓东, 等. 主动配电网最优潮流研究及其应用实例[J]. 中国电机工程学报, 2017, 37(6): 1634-1645.
GAO Hongjun, LIU Junyong, SHEN Xiaodong, et al. Optimal power flow research in active distribution network and its application examples[J]. Proceedings of the CSEE, 2017, 37(6): 1634-1645.
[19] XUE J K, SHEN B A. Novel swarm intelligence optimization approach: sparrow search algorithm[J]. Systems Science & Control Engine, 2020, 8(1): 22-34.
[20] 张潮, 陈静, 顾卫祥. 一种计及无功补偿的分布式电源优化配置方法[J]. 水电与抽水蓄能, 2020, 6(2): 36-41.
ZHANG Chao, CHEN Jing, GU Weixiang. Distributed power supply optimization configuration method considering reactive power compensation[J]. Hydropower and Pumped Storage, 2020, 6(2): 36-41.
[21] 刘一欣, 郭力, 王成山. 微电网两阶段鲁棒优化经济调度方法[J]. 中国电机工程学报, 2018, 38(14): 4013-4022, 4307.
LIU Yixin, GUO Li, WANG Chengshan. Economic dispatch of microgrid based on two stage robust optimization[J]. Proceedings of the CSEE, 2018, 38(14): 4013-4022, 4307.
[22] 阮贺彬, 高红均, 刘俊勇, 等. 考虑DG无功支撑和开关重构的主动配电网分布鲁棒无功优化模型[J]. 中国电机工程学报, 2019, 39(3): 685-695, 948.
RUAN Hebin, GAO Hongjun, LIU Junyong, et al. A distributed robust reactive power optimization model for active distribution network considering reactive power support of DG and switch reconfiguration[J]. Proceedings of the CSEE, 2019, 39(3): 685-695, 948.
[23] 任智君, 郭红霞, 杨苹, 等. 含高比例可再生能源配电网灵活资源双层优化配置[J]. 太阳能学报, 2021, 42(9): 33-38.
REN Zhijun, GUO Hongxia, YANG Ping, et al. Double- layer optimal configuration of flexible resources with high proportion of renewable energy distribution network[J]. Acta Energiae Solaris Sinica, 2021, 42(9): 33-38.
Bi-level optimization model of an active distribution network based on demand response
CHEN Qian, WANG Weiqing, WANG Haiyun
(Engineering Research Center of Education Ministry for Renewable Energy Power Generation and Grid-connected Control, Xinjiang University, Urumqi 830047, China)
The penetration of distributed generation (DG) is becoming higher and higher in the distribution network, and so it is difficult to completely eliminate the voltage ‘out of limit’ of the network. This paper constructs a bi-level optimization model considering equipment planning and the operation of an active distribution network. The upper model considers the capacity allocation optimization of DG, static var compensator (SVC) and capacitor bank (CB) in the network to reduce the investment and operational cost. In the lower model, the coordinated control of demand response (DR), on-load tap changer (OLTC), energy storage (ES) and DG are considered to improve voltage stability. From the characteristics of the model, a hybrid optimization algorithm based on the improved sparrow algorithm (CLSSA) and second-order cone (SOC) programming are used to solve the problem. The CLSSA algorithm is used to determine multi-dimensional variables externally to improve the solution speed, and the active management and control strategy of the network is obtained internally based on SOC programming. Finally, the modified IEEE33-bus system is used for simulation verification. The results show that the bi-level optimization model can effectively enhance the operation economy of the distribution network, improve the network voltage distribution and stabilize peak-valley difference.
distributed generation; reactive power optimization; active distribution network; demand response; bi-level model
10.19783/j.cnki.pspc.211516
2021-11-09;
2022-02-25
陈 倩(1996—),女,博士研究生,主要研究方向为配电网优化运行;E-mail: 971507673@qq.com
王维庆(1959—),男,通信作者,教授,博士生导师,主要研究方向为电力系统自动化和智能电网;E-mail: wwq59@xju.edu.cn
王海云(1973—),女,教授,博士生导师,主要研究方向为可再生能源发电与并网技术。E-mail: 327028229@qq.com
国家自然科学基金项目资助(52067020);新疆维吾尔自治区教育厅重点项目资助(XJEDU2019I009)
This work is supported by the National Natural Science Foundation of China (No. 52067020).
(编辑 姜新丽)
