基于网荷智能互动的精准切负荷策略

2022-09-02程维杰刘金生张俊芳张丽全郑健王璐玥

南方电网技术 2022年7期

程维杰，刘金生，张俊芳，张丽全，郑健，王璐玥

(1. 深圳供电局有限公司，广东深圳518000；2. 南京理工大学自动化学院，南京210094；3. 国电南瑞科技股份有限公司，南京211106)

0 引言

大容量远距离电能传输是目前我国电网乃至全球能源互联网的显著特征之一[1 - 4]。电力系统的不断扩大提高了网络结构的复杂性，新能源并网容量的增加降低了电力系统发电侧的受控能力、提高了电网中隐形故障和连锁故障的发生概率[5 - 9]。同时，随着智能电网以及智能用电方式的发展，网荷互动成为未来智能电网的重要发展方向[10 - 13]。通过网荷智能互动技术，可以将电网和负荷更加紧密地联系在一起，更有效地维持电网的稳定运行。

近年来，世界各国发生了数起电网停电事故，给电网的稳定运行和经济社会的正常发展带来了严重的影响。低频低压切负荷措施作为保护电力系统的重要措施之一，在电网受到严重扰动后保持电网系统性、避免出现大面积灾害性停电事故等方面发挥了重要作用。如何采取更加合理有效的切负荷策略，降低切负荷带来的不良后果，一直是目前研究的重点。文献[14]提出了一种基于随机森林的紧急控制策略，根据随机森林模型在线求解切负荷灵敏度，从而更合理地选择样本容量，提高预测的准确性以及紧急控制的有效性。文献[15]搭建了表征各负荷用户追求负荷损失代价最小化的非合作博弈模型，采用NSGA-II算法求解最优解，在保证重要负荷不断电的情况下，实现了精准切负荷以及各负荷用户间利益平衡的目标。文献[16]结合均值聚类法、人工神经网络法和层次分析法，提出了一种新的紧急切负荷控制模型，有效地减少了系统恢复动态稳定所需的时间。文献[17]提出了基于隐枚举法的快速分级优化切负荷优化方法，通过制定合理的搜索和剪枝策略，有效节约超过一半的计算时间，提高动作的速度。文献[18]提出了一种受端电网的跨电压等级分层模型，通过改进粒子群算法和AHP-模糊综合评价法得到优化切负荷方案，在有效消除线路过负荷的同时大幅减少计算时间。

综上所述，现有的切负荷方法通常仅从负荷侧考虑，忽视了电网侧和负荷侧之间的交互影响，电网参数的变化会对负荷造成影响，而负荷的变化又会反过来影响电网的参数。因此，本文基于网荷互动，兼顾电网侧和负荷侧，根据电网频率和电压的特性整定电网的功率缺额和切负荷的动作轮次信息，并基于改进的萤火虫算法，提出了一种基于低频低压网络的网荷智能互动系统的优化切负荷策略，提高了紧急情况下切负荷动作的快速性与精确性。

1 网荷智能互动下的切负荷理论

对于电力系统来说，网荷智能互动是增强系统运行安全性、可靠性与经济性的重要手段。当电网发生故障出现功率缺额等问题时，负荷侧要根据电网侧的频率、电压等参数的变化情况及时采取措施消除故障，从而维持系统的正常运行。本文从网荷智能互动出发，根据系统遭到扰动后的频率、电压特性计算出电网的功率缺额后，采用轮次法将需切除功率额分配到切负荷动作的各个轮次中，通过网荷智能互动以有效抑制频率和电压的下降，维持电网频率和电压在允许范围内。轮次法通常分为基本轮和特殊轮，基本轮的作用是通过切除一定量的负荷防止频率和电压进一步下降，特殊轮的作用是通过切除少量负荷以避免系统切负荷动作后的频率悬浮于某一较低值。

系统惯量中心频率fCOI可以表示为：

(1)

式中：fi为第i台发电机频率；Hi为第i台发电机惯性时间常数；Heq为系统等效惯性时间常数。

对式(1)进行求导可以得到惯量中心频率变化率的表达式为：

(2)

在电力系统中单台发电机的转子运动平衡方程为：

(3)

式中：ΔPi为单台发电机的不平衡功率；fN为系统额定频率。

系统中总的不平衡功率标幺值形式ΔP可以通过各台发电机的不平衡功率相加得到。

(4)

假设系统中实际功率缺额的有名值为Pdef，则式(4)也可写为：

(5)

式中：Si为第i台发电机的额定功率；Seq为系统中所有发电机的额定功率之和。

由式(4)—(5)可以得到功率缺额的表达形式。

(6)

考虑网荷智能互动情况下系统中的旋转备用容量和可调负荷容量，忽略系统损耗和频率变化对负荷功率的影响，并结合功率缺额及负荷有功功率的实时值，故障后系统实际切负荷量为[19]：

(7)

式中：PSR为系统中旋转备用与可调负荷的容量；PL0,i为故障前母线i的有功功率值；V0,i为故障前母线i的电压值；Vi为故障后母线i的电压值；m为系统中的母线总数；αi为负荷-电压变化特性指数。

本文提出的自适应切负荷方法将基本轮分为5轮，特殊轮分为3轮。在整定基本轮的动作参数时，功率缺额计算公式中的惯量中心频率变化率由前一轮切负荷后的实时频率变化率代替，以此提高切负荷量计算的自适应性。

由式(7)可以计算出第j轮基本轮的实际切负荷量。

Pshed,bas,j=kjPshed,j

(8)

式中：Pshed,j为第j轮切负荷动作时的功率缺额；kj为第j轮基本轮的切负荷比例系数，其取值由电网规模的大小和频率变化dfCOI,j/dt共同决定(fCOI,j为第j轮切负荷的系统惯性中心频率)[19]。

特殊轮共设置3轮，每一轮的整定规则相同，动作频率均为49.5 Hz，动作延时均为5 s，切负荷量设定为：

Pshed,spe,i=kspe,iPshed,i

(9)

式中：Pshed,i为第i轮切负荷动作时的功率缺额；kspe,i为第i轮特殊轮切负荷比例系数，取值范围一般为[0.08,0.1]。

2 改进萤火虫算法的优化切负荷策略

2.1 优化切负荷模型

本文根据切负荷量最小原则建立切负荷优化方案的数学模型如式(10)所示。

(10)

式中：函数F为实际最小切负荷量；ΔP为实际切负荷量与需切量的差值；Pload,i为第i个节点的切负荷量，且Pload,i≥0；Pshed为需切除负荷量；i为切负荷对象；n为备选切负荷对象数量。

根据上述目标函数建立的优化切负荷模型主要有以下几个约束条件如下。

1)系统内实时切负荷总量约束

(11)

式中：Pload,i为第i个节点的切负荷量；Pper,max为系统内所允许的最大切负荷量，由系统实际运行情况决定；n为备选切负荷对象数量。

2)系统稳态频率约束条件

fmin≤fafter≤fmax

(12)

式中：fafter为切负荷动作后的系统稳态频率；fmax和fmin分别为稳态时系统频率的上、下限。

3)母线节点稳态电压约束条件

Vi,min≤Vi,after≤Vi,max

(13)

式中：Vi,after为切负荷动作后母线i的稳态电压；Vi,max和Vi,min分别为稳态时母线i电压的上、下限。

2.2 改进萤火虫算法

萤火虫算法是一种基于萤火虫群体移动规律而发展起来的智能优化算法[20 - 22]。在萤火虫算法中，每只萤火虫都有各自的决策域，萤火虫群体在各自的决策域内不断地向较优个体移动，最后大部分萤火虫都会汇聚在目标函数适应值最高的萤火虫附近，从而实现优化的目的。

萤火虫算法与其他智能算法相比，具有稳定性优越、操作能力强等优点，因而被广泛应用于各个领域。但萤火虫算法搜索的随机性也不可避免地导致了其全局搜索能力的降低和收敛速度的不稳定[23 - 25]。因此，本文对基本萤火虫算法进行改进，以提高萤火虫算法的搜索速度与全局寻优能力。

改进萤火虫算法主要由萤火虫初始化、荧光素值更新、萤火虫移动以及决策域更新这4个步骤组成。

1)萤火虫初始化

根据优化模型确定搜索空间，并随机分布萤火虫种群，萤火虫个体拥有相同的初始荧光素值l0和初始决策域半径r0。但随机初始化萤火虫种群会影响算法的收敛速度，不利于算法的快速寻优。本文结合切负荷问题，利用节点电压灵敏度对萤火虫种群进行初始化，以得到更合理的初始解，加快搜索速度。

定义节点电压灵敏度为：

(14)

式中：Vi为节点i的电压；Pi为节点i的功率。

从式(14)可以看出，节点的电压灵敏度越大，该节点功率变化对电压的影响就越大，节点的稳定性就越差。这些节点在电网运行过程中较为薄弱，当电压出现失稳时就是从这些薄弱节点开始扩散，进而影响整个电网。因此在切负荷动作时，优先切除这些薄弱节点上的负荷能够使电网更快地恢复稳定。

2)荧光素值更新

萤火虫荧光素值表征萤火虫个体的优劣，它与两个参数有关，一个是萤火虫上一次迭代时的荧光素值，一个是萤火虫当前位置的适应度值。荧光素值的计算公式如式(15)所示。

li(t)=(1-ρ)li(t-1)+γJ(xi(t))

(15)

式中：ρ∈[0,1]，为荧光素挥发因子；γ∈[0,1]，为荧光素更新率；xi(t)为第t次迭代时萤火虫i所处位置；J(xi(t))为第t次迭代时第i个萤火虫所处位置的适应度值；li(t-1)和li(t)分别为第t-1次迭代和第t次迭代时萤火虫i的荧光素值。

3)萤火虫移动

每只萤火虫在其邻域集内以一定概率向荧光素值较高的个体移动，概率的计算公式如式(16)所示。

(16)

式中：Ni(t)为第t次迭代时第i个萤火虫的邻域集；lj(t)、li(t)和lk(t)分别为第t次迭代时第j、i和k个萤火虫的荧光素值。

若萤火虫i在其邻域集内以寻找到更优个体j，根据式(17)更新其位置。

(17)

为加快萤火虫的收敛速度，以免萤火虫陷入局部最优解，本文从两个参数考虑萤火虫步长的变化情况，一是迭代次数，二是第t代最佳萤火虫的位置。一方面，萤火虫的步长应随迭代次数的增加而减小；而另一方面，萤火虫的步长又应随该萤火虫与第t代最佳萤火虫距离的减小而减小。综合上述两个因素，本文对萤火虫的步长按式(18)进行更新。

(18)

式中：t为当前迭代次数；Nt为预先设定的最大迭代次数；xb(t)为第t次迭代时最佳萤火虫所处的位置。

若萤火虫个体在其邻域集内没有发现比其荧光素值更高的个体，则停止搜索，这有可能延缓搜索的速度。因此，为了充分利用萤火虫的搜索能力，提高搜索速度，本文以最小步长对搜索过程中保持静止的萤火虫进行扰动，让其随机搜索，此时萤火虫位置的更新如式(19)所示。

(19)

式中：smin为迭代过程中的最小步长；C为n维随机向量。

在萤火虫位置的更新过程中，通过步长的动态更新和邻域集为空时的随机搜索这两方面的改进，可以充分利用每个萤火虫的搜索能力，加快搜索的速度，同时还能够有效地增强全局搜索能力，从而更好地实现寻优的目的。

4)决策域更新

萤火虫位置更新后要根据邻域集中萤火虫的数量改变萤火虫决策域的大小，以加快搜索的速度，决策域半径的更新如式(20)所示。

ri(t+1)=min{rs,max{0,ri(t)+β(ny-|Ni(t)|)}}

(20)

式中：β为萤火虫的动态决策域更新率；rs为萤火虫感知半径的上限；ny为邻域集内萤火虫数量的限值；|Ni(t)|为第t次迭代时第i个萤火虫邻域集内萤火虫的数量；ri(t)和ri(t+1)分别为第i个萤火虫在第t次迭代和第t+1次迭代时的决策域半径。

基于改进萤火虫算法的优化切负荷策略的流程如图1所示。

图1 基于改进萤火虫算法的优化切负荷流程Fig.1 Optimized load shedding process based on improved glowworm swarm optimization

3 仿真分析

以某地区电网为例，该地区电网通过电源G1与外部电网相连，同时有4台本地区的发电机G2—G5为各个负荷供电，电网内负荷总功率为3 182 MW，各负荷节点均配置了低频低压切负荷装置。该地区电网的拓扑结构如图2所示，电网中各节点负荷数据如表1所示。

图2 某地区电网拓扑结构Fig.2 Topological structure of a certain area power grid

表1 各节点负荷数据Tab.1 Load data of each node

根据前述对网荷智能互动基础下切负荷理论的分析并结合该地区电网的实际情况，本文切负荷设置5轮基本轮，3轮特殊轮，具体的轮次参数信息如表2所示。

表2 低频低压自适应切负荷轮次设计Tab.2 Low-frequency and low-voltage adaptive load shedding rounds design

初始时该地区处于稳定状态，运行一段时间后，电源G1和母线2的联络线故障断开导致该地区电网与外部电网解列形成局部孤网，系统初始功率缺额为531.86 MW。

针对该电网发生的上述故障，电网中各节点处配置的低频低压切负荷装置根据表2所设计的轮次动作。为了突出文中所提出的改进萤火虫算法在切负荷优化问题上的优势，本文将其与遗传算法和基本萤火虫算法切负荷的结果进行比较，对比结果如表3和图3所示。

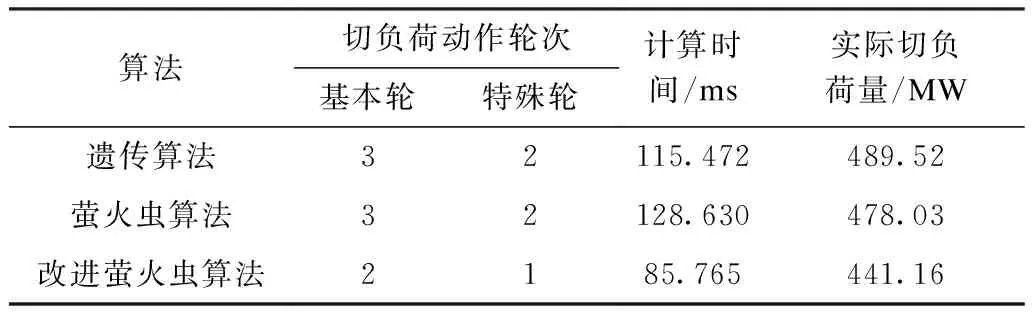
表3 不同切负荷算法结果对比Tab.3 Comparison of results of different load shedding algorithms

图3 系统频率变化曲线Fig.3 Change curves of the system frequency

从表3中的数据可以看出，基于改进萤火虫算法的切负荷方案相比于传统智能算法的切负荷方案而言，切负荷动作的轮次明显减少，只需要2轮基本轮和1轮特殊轮就能完成切负荷动作，而传统的遗传算法以及萤火虫算法均需要3轮基本轮和2轮特殊轮才能够完成切负荷动作。从图3可以看出基于改进萤火虫算法的切负荷方案能够更迅速地切除相应负荷使电网恢复稳定。改进萤火虫算法计算切负荷优化方案的耗时比传统智能算法的计算提高了25%以上，大大减少了计算优化方案的时间。同时，采用改进的萤火虫算法时电网的实际切负荷量也降低至441.16 MW，比采用遗传算法时的实际切负荷量少了48.36 MW，比采用基本萤火虫算法时的实际切负荷量少了36.87 MW，明显地降低了实际切负荷量，能够以更低的代价维持电网的稳定运行。

为了直观地体现出改进萤火虫算法在切负荷优化方案的计算时间和实际切负荷量两方面的优势，将备选切负荷对象数量从14个增加到22个时，优化切负荷方案的计算时间以及实际切负荷量的变化情况，结果分别如图4—5所示。

图4 切负荷优化方案计算时间对比Fig.4 Comparison of calculation time of load shedding optimization schemes

图5 实际切负荷量对比Fig.5 Actual load shedding comparison

从图4—5可以看出，随着备选切负荷对象数量的增加，3种算法求解切负荷优化方案的计算时间都呈上升趋势，而实际切负荷量都呈下降趋势。其中，本文所提出的改进萤火虫算法同遗传算法以及基本萤火虫算法相比，不仅能够有效地减少切负荷优化方案的计算时间，而且还能够明显地降低电网的实际切负荷量。此外，备选切负荷对象的数量越多，改进萤火虫算法在切负荷问题上的优势就越明显，从而为紧急情况下的切负荷动作和决策争取更多的时间，以更低的代价维持电网的安全稳定运行。