圆线圈平面磁场分布及其电感的计算与分析研究
2022-09-01张克生
张克生
(江苏安全技术职业学院 基础课教学部,江苏 徐州 221011)
0 引言
通电线圈的磁场分布以及电感系数已有多篇论著进行相关研究[1-5],然而在实际求解线圈空间磁场分布和电感系数时,存在着数学计算公式复杂、计算量大等相关问题[6]。通电圆线圈是电磁学理论及应用中最典型的模型之一,虽然该模型简单,但是对于其空间磁场分布及其电感系数的计算比较复杂。张德根等[7]用线电流模型给出了圆线圈磁场分布的积分表达式;杜珊等[8]通过理论与实验相结合研究了载流圆线圈平面内的磁场分布情况;张星辉等[9]从一个圆电流的矢势出发, 导出了任意两共轴圆线圈间互感系数的函数表达式;左晓旺等[10]分析讨论了两共轴平行圆线圈之间的互感系数与线圈的尺寸、相对位置的关系等。
对于实际载流圆线圈来说,通常具有一定的截面积,将其简化为线电流模型处理往往存在一定的问题,如线圈自身所在位置的磁场无法计算,从而不能由圆线圈的磁通量来计算其自感系数。例如圆形截面的载流圆线圈,线圈的平均半径R和截面半径a对其磁场分布和电感系数的影响缺乏定量的计算,同时对圆线圈侧面边界处磁场如何变化等问题缺乏定性的分析,因此有必要对线圈平面的磁场分布和电感系数计算作进一步分析研究。
1 圆线圈平面磁场分布
1.1 计算模型与方法
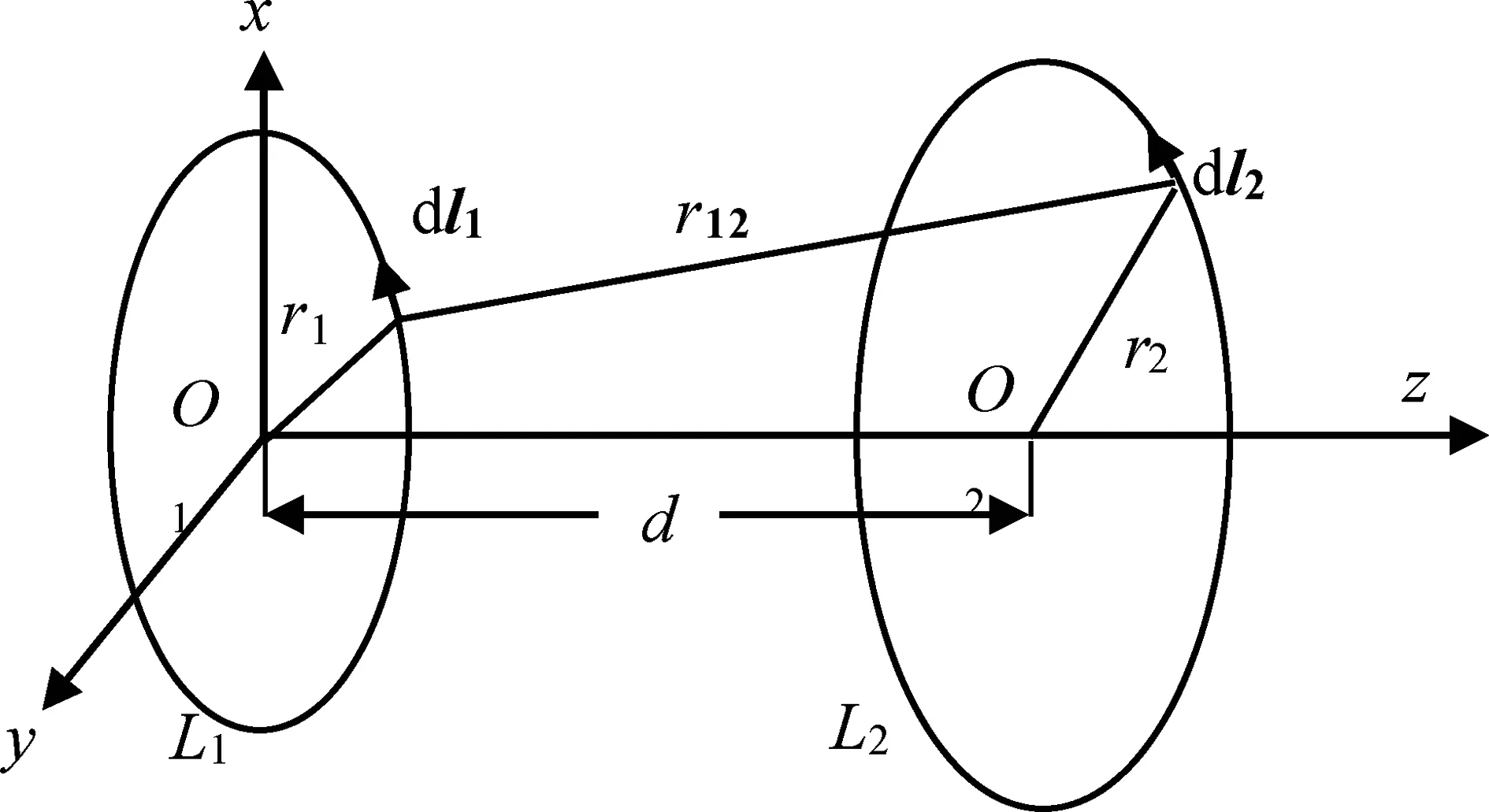
如图1所示,在平均半径为R、截面半径为a的载流圆线圈所处的平面上,r为线圈平面上任意一点与圆线圈圆心之间的距离。当电流I顺时针通过圆线圈时,根据对称性及右手螺旋关系,可以判定圆线圈内部磁场垂直向里,圆线圈外部磁场垂直向外。在圆线圈导体外部,即r>R+a或r (1) 式中:μ0为真空磁导率。 图1 载流圆线圈及其截面 在载流圆线圈内部,即R-a≤r≤R+a,当a< (2) 式中:μ为线圈导体材料的磁导率;μr为相对磁导率。整个圆线圈所在平面的磁场分布表达式可表示为: (3) 根据上述表达式,其中包含的积分表达式可利用Mathematica软件进行数值求解,可以得到圆线圈平面沿着其径向的磁场分布。例如当R=0.1 m,a=0.3 mm,I=10 A时,导体材料为铜,在温度为293 K时相对磁导率μr为0.999 990。r在0~0.2 m范围内磁感应强度大小分布曲线如图2所示。 根据上述表达式,在线圈内外侧面边界处,即r=R-a和r=R+a,磁场计算值分别按式(1)和式(2)进行计算,分析线圈内外侧面边界磁场的连续性。例如当I=10 A,R=0.1 m时,边界处磁场计算数据如表1所示。当圆线圈平均半径(R=0.1 m)保持不变,随着线圈截面半径a的增大,两种模型计算结果的相对误差不断增加。如果要求两者计算结果的相对误差小于3%,则a与R的比值应小于0.015。在圆线圈内侧面边界,即r=R-a处,线电流模型计算值大于长直导线模型计算值,在圆线圈外侧面边界,即r=R+a处,线电流模型计算值小于长直导线模型计算值。通过表1的数值计算结果可以看出:当a/R<0.015时,圆线圈内、外侧面边界处两种模型计算的磁场值非常接近,边界处磁场近似连续变化;当a/R>0.015时,边界处两种模型计算的磁场值有较大的跃变。在计算精度要求高的情况下,随着截面半径的增大,用长直导线模型计算其内部磁场误差较大,需要考虑新的计算办法。 图2 圆线圈平面径向磁场分布曲线B(r)(0≤r≤0.2 m) 为验证圆线圈平面磁场分布表达式的正确性,利用FB516型亥姆霍兹线圈磁场实验仪,对圆线圈平面的磁场进行定量测量,图3为仪器测量实物图。实验仪器选用先进的玻莫合金磁阻传感器,该传感器与传统使用的探测线圈、霍尔传感器相比,具有灵敏度高、抗干扰性强、可靠性好及便于安装等诸多优点。实验待测线圈的匝数为100,平均半径为10 cm,恒流源输出电流设置为100 mA,等效电流为10 A,使其与上述理论计算的电流相等。在线圈所在的平面上测量磁场分布,得到平面上磁场分布的实验值和计算值曲线,如图4所示,两条曲线基本重合,两者间的相对误差非常小,说明实验值与计算值是相符合的。 图3 磁阻传感器测量线圈磁场 图4 实验值与计算值曲线 对于圆线圈的自感(L自)通常利用式(4)进行近似简便计算。 (4) 在计算精度较高的情况下,随着圆线圈几何尺寸的不断增大,近似计算公式的误差将会增大,必须重新考虑新的计算方法。 单个圆线圈的自感为内自感(L内)与外自感(L外)之和: L自=L内+L外 (5) 利用圆线圈平面上的磁场分布表达式,先计算圆线圈内部的磁通量,再根据电感的定义计算外自感,其中圆线圈内部的磁通量为半径r=R-a面圆内磁感线的条数。根据圆线圈平面上磁场分布的中心对称性,分别得到磁通量(Φ)的表达式(6)、外自感(L外)表达式(7)和自感(L自)的表达式(8)。 (6) 式中:S为圆线圈内部面元。 (7) (8) 如图5所示,单个圆线圈的外自感可以看成平行共轴且在同一平面的两个半径分别为R和R-a的圆线圈互感。对于两个平行共轴圆线圈L1和L2,其半径分别为r1,r2,线圈之间的距离为d。根据诺依曼公式,两个线圈之间的互感系数(M)为: 图5 两平行共轴圆线圈 (9) (10) 利用上述互感系数的表达式,将r1=R,r2=R-a代入式(10)可得单个圆线圈外自感与自感的表达式: (11) (12) 如上所述:第1种电感系数的计算方法是先给出磁通量的表达式,再得到电感系数,计算过程容易理解,缺点是计算的表达式为复杂二重积分,利用数值计算需要较长时间;第2种计算方法得到的表达式为一重积分,数值计算速度快。 分别利用式(4)、式(8)和式(12)计算圆线圈的自感系数,其中式(8)和式(12)积分可以直接利用Mathematica软件得到计算值。根据表2和表3中的数据,可知两种数值计算的结果几乎相等,随着线圈尺寸的增加,两种数值的计算值与近似公式计算值的差值增大。 表2 截面半径a=0.3 mm时的自感系数计算值 表3 平均半径R=10 cm时的自感系数计算值 当线圈截面半径a一定时,其电感系数L与线圈的平均半径R近似成正比;当线圈平均半径R一定时,其电感系数L随线圈截面半径a增大而减小,其原因在于平均半径R不变时,外自感会随截面半径增大而减小,而内自感不变,总自感减小。 本文对圆形截面圆线圈平面磁场及其电感系数进行了相关计算与分析,求解计算过程中没有使用比较烦琐的第一类、第二类椭圆积分等特殊函数,也没有通过编程求解双重积分值,而是直接利用Mathematica软件强大的数值计算功能,计算过程简洁,确保物理量概念清晰。通过精确的数值计算结果可知:当截面半径a与平均半径R的比值逐渐增加时,按式(3)计算圆线圈平面磁场则会引入较大误差,尤其是圆线圈边界附近的磁场;同时其自感系数的计算还需要进一步深入探讨。
1.2 边界处磁场的连续性

1.3 实验值与计算值比较


2 圆线圈的自感系数


2.1 第1种计算方法
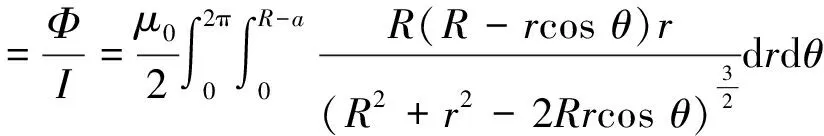

2.2 第2种计算方法

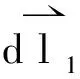


3 电感系数的数值计算与分析


4 结语
