基于改进的樽海鞘算法优化BP 神经网络参数的分类识别方法

徐任倩XU Ren-qian；汪超WANG Chao；王璐WANG Lu

（①安徽工业大学管理科学与工程学院，马鞍山 243002；②安徽工程大学土木建筑工程学院，芜湖 241000）

0 引言

生物的神经十分复杂，为了探究其中奥秘，很多研究学者投入到神经研究过程中，在研究过程中，得到了灵感发展出人工神经网络。人的大脑构造非常复杂，它是由大概1011所神经元组成的，这些神经元保持着高度相联系，基本一个神经元就会连接104个神经元[1]。在研究生物神经时找到了人工神经网络的发展方向，也就是起源，用数学方式表示神经元，用来模仿生物的神经元的特点——神经网络高度联系。不同的神经的拓扑结构也不同，所以我们可以将人工神经网络分为反馈和前向两种。主要的反馈网络有：Hop-field 神经网络、Hamming 神经网络、BAM（Bidirectional Associative Memory）网络。而后者主要有BP（Back Propagation）神经网络、单层或多层感知器等。其中BP 神经网络是最精华部分，我们重点讲述该神经网络，它的主要作用是对于一些非线性函数进行特殊变换，使空间由输入变为输出。

神经网络的研究结果到现在有很多，各种各样，但比较完善的理论还是BP 神经网络，它具备良好的泛化能力（合理响应的能力）、自适应、鲁棒性和学习性。不是所有的BP 神经网络都能处理任何非线性函数，但单层输入层、隐含层和输出层的可以任意处理，不管精度是多大。BP 神经网络现在已经被广泛应用在其他方面，比如处理图像，函数逼近，识别模式。但是，BP 算法也存在着一些缺点，例如收敛速度差，很容易掉入局部最优的陷阱里，只有经验公式来指导如何确定神经元个数以及网络层数，并且当问题比较复杂或难以获得的梯度信息时，BP 神经网络可能会束手无策。BP 神经网络的权重训练采用的是梯度下降法，这样很容易达到局部最优，而不能得到全局最优，我们可以引入一种自适应的学习方法得到权重和阈值以此避免出现这种情况。本文引入改进的樽海鞘算法优化BP 神经网络的权重和阈值。

1 BP 算法

BP 神经网络从结构上看，分成三层或以上，其中隐含层可以一层也可以多层，夹在输入层与输出层之间。如果隐含层只有一层隐含层，那么此时的BP 网络结构是最简单的，如图1 所示。现在我们定义一些变量，假设该网络输入n1个和输出n2个，有m 层隐含层。f1、f2是隐含层、输出层函数，则隐含层输出值为bj，隐含和输出层阈值为θj、θk。隐含层连接输入层与输出层权重为wij，vjk。然后我们可以得到BP 神经网络输出的值Zk，定义为tk为期望输出的值，那么bj有等式：

输出层值Zk的计算公式如下所示：

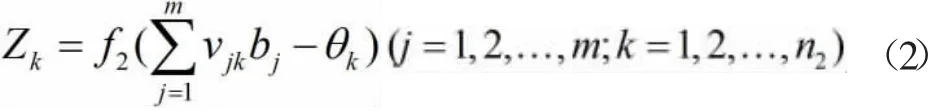
当输出与期望的输出不同，即Zk≠tk，此时存在误差e，其定义如下：

BP 神经网络间神经元之间传递的函数有许多种，常见的有：阈值型、概率型、分段线性、线性和非线性。多层网络时，每层网络选择函数既可以是同类的，也可以选择异类。本文所使用的BP 算法采用的传递函数是双曲正切S型传递函数和线性传递函数。网络训练是一个不断调整权重和阈值的过程，在网络开始训练前，设定一个阈值E，如果输出误差e 小于等于E，则结束网络训练，然后将预测样本输入训练好的网络当中就可以得到预测结果。

大多数都是最简单的BP 神经网络，它包括输入层、输出层以及中间单层隐含层，它的性能由网络结构（隐藏神经元）、权重、阈值和学习率等决定。隐含层神经元数目如果太少的话，BP 神经网络此时需要通过加大训练次数得到更好的结果；但是隐含层太多的神经元数目也不是什么好事，那么训练时间会拉长，而且还容易出现过拟合。所以需要选择最合适的神经元个数，经过多次验证，最后得出经验公式，如式（4）所示：

式中，输入层、输出层、隐含层的神经细胞数分别为bm、bn、bl；ba 是自然数，范围从0 到10。

2 基于改进樽海鞘算法的BP 模型

在2017 年，Mirjalili 等[2]提出了一种新的算法，命名为樽海鞘算法（SSA：Salp swarm algorithm）。它是一种群体算法，具有智能化，其想法来自于樽海鞘们在海洋中导航寻找食物时所产生的群体现象。它在搜索最优解的时候，樽海鞘会盘旋成一个樽海鞘链，链中最前面的是领导者，剩下的是追随者。在樽海鞘算法中引入无标度网络与惯性权重，加强算法跳出局部最优解的能力，提出一种新的改进樽海鞘算法-高效樽海鞘算法（E-SSA：Efficient salp swarm algorithm）。

领导者向前面搜索最优位置，领导者的位置更新公式为：

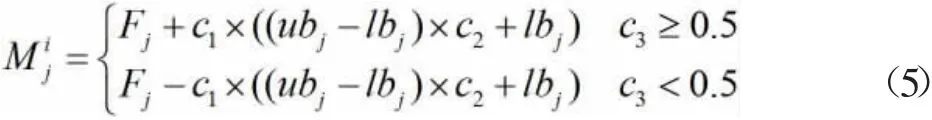
本文首先生成一个无标度网络来映射追随者的关系，然后在追随者樽海鞘的更新公式中加入基于种群多样性反馈的惯性权重，具体公式为：

式中：nbd（i）代表第i 个樽海鞘与之有拓扑关系的所有邻居。惯性权重W 的值越小，算法越有可能偏离局部最优而收敛到最优。惯性权重的计算公式如式（7）所示：

其中C 代表多样性度量，lmax代表最大迭代次数。多样性度量可由以下公式计算：

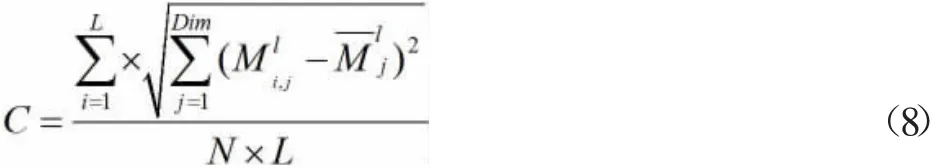
在公式（8）中，N 指的是种群中个体数，Dim 代表的是变量的维度。代表第i 个个体的第j 维的变量，代表种群所有个体在第j 维的平均值，搜索空间的对角线距离

使用E-SSA 优化BP 神经网络的权重和阈值的流程图如图2 所示。

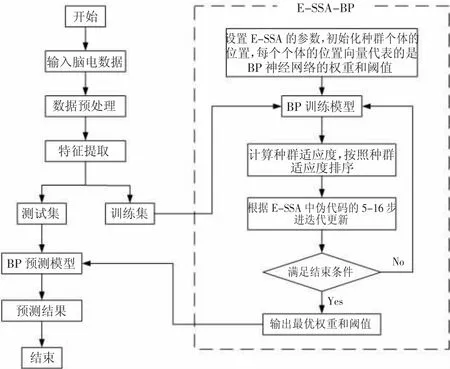
图2 E-SSA-BP 的训练和分类流程

3 基于脑电数据集的分类识别

3.1 计算方法与参数

本文优化权重和阈值的方法利用BCI2003 公开的运动想象脑电信号数据集对E-SSA 验证，引入先进的算法，有粒子群优化算法（PSO：Particle swarm optimization）、樽海鞘算法、差分进化算法（DE：Differential evolution）、权重自适应樽海鞘算法（WASSA：Weight factor and adaptive mutation salp swarm algorithm）和疯狂自适应樽海鞘算法（CASSA：Crazy and adaptive salp swarm algorithm）对BP 神经网络进行参数优化从而去看各个算法的优化效果。其中DE 是一种启发式算法，具有随机性，它通过对种群采用变异、交叉和选择三种进化操作使算法的解逼近于全局最优解[3]。PSO 是从鸟类的觅食过程研究出来的，其是一种群体算法，具有智能化。它是通过整个种群中的每个粒子相互帮助合作以及共享彼此信息来逼近全局最优解[4]。WASSA是Wu 等[5]在樽海鞘算法中的种群位置加入了权重因子以此来平衡全范围勘探与局部开发，而且为了避免收敛过早和进化停滞，在进化过程中引入自适应突变策略。CASSA是张达敏等[6]在2019 年提出的一种改进樽海鞘算法。他们为了保护种群多样性，在樽海鞘算法生成初始种群时引入Tent 混沌序列和在食物位置引入疯狂算子，为了保持局部搜索能力与全局搜索能力的良好平衡，在追随者位置更新公式中添加了自适应惯性权重。这些算法在解决不同条件下的离散优化问题或连续优化问题方面有各自的优势。

运动想象脑电信号数据集可以从http://bbci.de/competition/ii/下载，它是一个25 岁的健康女性坐在椅子上通过看着屏幕上随机出现左或者右的提示想象左右手的运动控制反馈器的脑电信号数据集，总共实验时长为9s，最先的2s 屏幕没有任何提示，2s 末有一个提示音告诉被试准备动作，第3s 屏幕出现提示被试开始相应的运动想象。该实验记录了C3、C4 和Cz 三个通道，采样频率为128Hz，总共进行了7 次实验，每次实验有40 个样本，每个样本时长为9s，最终得到一个140 个样本的训练集和140个样本的测试集。

对上述的脑电数据集的脑电信号进行滤波，保留8-30Hz 范围内的脑电数据。每个通道提取三个时域特征值（峰值、均方根值、一阶差分绝对值的均值）、一个频域特征值（Welch 法）和五个非线性动力学特征值（样本熵、排序熵、递归图中的ENTR、赫斯特指数、希尔伯特-黄谱熵）进行特征组合，得到了140×27 的训练集和测试集。训练集用于优化算法进行参数寻优，测试集测试得到最优参数的BP 神经网络性能。

为了避免偶然性，每个算法在进行参数寻优时运行10 次。为了体现算法的公正性，我们将不同算法都在一个环境中运行：使用Windows7 系统计算机，编程软件为Matlab，CPU 为Inter Core TM 3.2Hz。本文设置bm=27；bn=1；bl=7。种群规模为100，迭代次数最大值是40。

3.2 结果分析

表1是经过参数寻优后得到的BP 分类模型在训练集和测试集的平均准确率，图3 是六种优化算法的迭代曲线图。从图3 可以看出除了DE 的结果比较低，其他四种算法与本文提出的方法结果比较接近。在刚开始的时候，E-SSA 收敛速度最快，中间有一段时间陷入了局部最优解，停滞不前，但是后来还是跳出了局部最优解，并且得到了最好的结果。本文针对BCI2003 的运动想象的数据集在训练集和测试集比例为1∶1 时最终得到的分类准确率为79.50%。田强强在BCI2003 数据集中，基于事件相关同步去同步（ERS/ERD）进行特征提取后的分类准确率为76.43%；基于自回归模型（AR）进行特征提取后的分类准确率为66.43%；基于联合回归模型（JR）进行特征提取后的分类准确率为73.57%；基于公共空间模式（CSP）进行特征提取后的分类准确率为72.86%[7]。黄等人[8]利用频域特征对该数据集分析得到了78.85%的分类准确率。由此可以看出E-SSA-BP 模型性能更好。

表1 六种算法运行10 次分类结果统计表

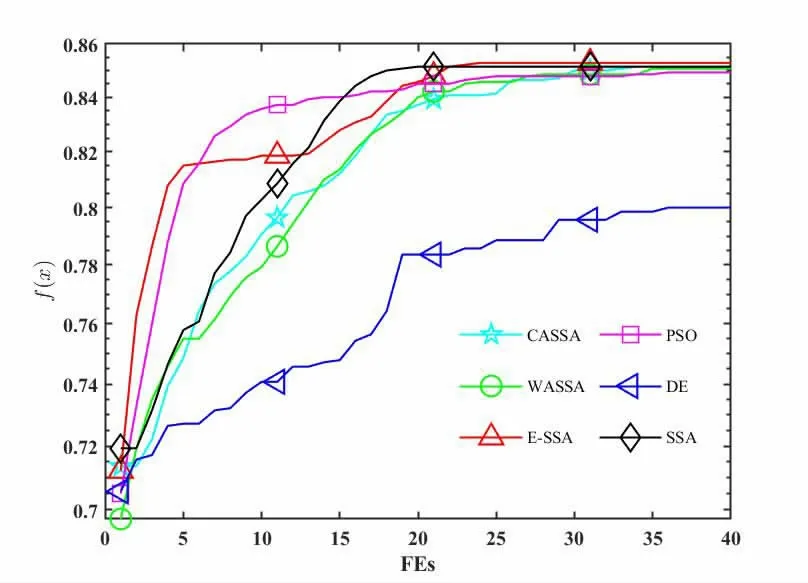
图3 六种优化算法的迭代曲线图

4 结语

在本文中，对于BP 神经网络容易掉入局部最优陷阱和不能快速收敛这两个问题，所以为了平衡该神经网络的局部和全局搜索能力，我们对此提出使用E-SSA 寻找BP神经网络中最好的连接权重值和阈值。本文使用BCI2003数据集对E-SSA-BP 模型进行实验验证，实验结果表明，E-SSA-BP 模型提高了分类准确率。