顾及时空“点-线”关联特征的出行轨迹描述模型

林 艳，贺日兴，陈 军，李佳田，张文宇

1. 中国人民公安大学信息网络安全学院，北京 100038； 2. 首都师范大学资源环境与旅游学院，北京 100048； 3. 国家基础地理信息中心，北京 100830； 4. 昆明理工大学国土资源工程学院，昆明 650093

关联出行反映了出行目标之间的时空交互，是时空认知研究的基础问题之一[1-3]，也是城市规划、交通出行、传染病防控、犯罪侦查等领域的研究热点。以往研究多从宏观层面，采用公众出行、出租车等轨迹数据，结合关联的POI、土地利用类型等数据，揭示出行数据所蕴含的道路交通状态、城市居民出行规律、城市结构及其他社会问题[4-8]。近年来，随着疫情防控、特殊车辆监测、犯罪侦查等精细化需求，很多学者从微观层面研究个体目标之间的接触、同行/伴随等关联出行行为：如通过分析出行轨迹在时间和空间上的邻近性，检测COVID_19病例的密切接触者[9]；通过分析出行个体共处的时间长短、次数等，检测交通个体的潜在同行人员[10]；通过分析刷卡时间间隔和地点，判断高校学生是否存在社会网络关系[11]；基于时间和空间约束关系，分析出租车、运钞车等特殊车辆的可疑伴随模式[12-15]；针对反恐情报时空轨迹数据，挖掘涉恐群体中的伴随模式等[16-17]。

然而，出行轨迹作为人的主观选择结果，蕴含着出行个体更复杂的主观意图。以犯罪分子为代表的某些特殊目标，如犯罪分子A在旅馆等待犯罪分子B，接头后二者共同去往某地，等待被害人C出现后实施犯罪，关注犯罪团伙、犯罪分子与被害人之间的时空特征规律并识别接头、等待等关联出行行为，是案件侦查、犯罪防控的重要理论基础。

当前的轨迹关联分析研究是以识别接触、同行/伴随关系中的某一种模式为目的，主要包括3种方法：①基于线模型的轨迹相似度判断：对原始轨迹化简后，表示为线要素，基于距离、时间度量计算同行轨迹的相似度[18-20]，从而判断出行是否存在关联。②基于序列点模型的时空约束关系判断[12-17,21-22]：将轨迹表示为序列点要素，判断在某段时间上连续、且在空间上处于特定范围内的轨迹点，能够识别出共同停留点/接触点、同行路段两种关联出行模式。③基于Stop/Move点模型的拓扑关系计算[23-25]：采用Stop/Move模型描述轨迹数据中的停留点和移动点[23-24]，在此基础上，根据空间拓扑关系，得到轨迹与周边地理要素之间共13种关联关系[25]。

本质上，上述研究分别采用点要素或线要素来描述个体出行轨迹，导致在此基础上的关联出行分析要么关注“细节点”、要么关注“整体线”，从而只能识别“共点”或“共线”两种关联出行类型，而无法区分和描述共点和共线关系中的“等待、接头”等更复杂的关联出行模式。为此，本文首先提出一种顾及“点-线”特征的出行轨迹描述模型；然后，在此基础上，基于时空拓扑关系提出关联出行的轨迹判别方法，能够描述19种不同的关联出行模式；最后，通过试验对比，表明本文方法能够更清晰地识别关联出行轨迹所隐含的犯罪主观意图。

1 出行轨迹描述模型

出行轨迹描述是关联行为分析的前提和基础。在犯罪团伙、犯罪分子与被害人之间的关联分析中，接头、等待等关联行为需要关注轨迹中的停留地点，而同行等关联行为需要关注移动的路线，因此，出行轨迹描述模型需要同时兼顾轨迹的细节“点特征”和完整“线特征”，为此，本节首先介绍顾及“点-线”特征的出行轨迹描述模型。

1.1 轨迹点及其时空特征

如图1所示，在三维空间中，绘制任意一条出行轨迹，如黑色线条。该轨迹由一系列有序结点构成〈p1,p2,…，pn〉，这些点的类型包括停留点(简记为P′)、移动点(简记为P)两种。即对于任意轨迹结点p，其轨迹点类型Type(p)={P、P′}。

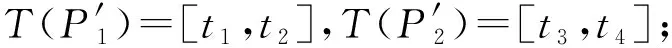
图1 轨迹点的时空特征Fig.1 The spatio-temporal characteristics of trajectory points

1.2 轨迹线的时空特征及基本单元

基于线的轨迹描述不是简单地将所有点顺序连接，而是从微观层面，分析最小的线单元，这是因为在对两条轨迹进行时空拓扑关联计算时，前提是要在统一的时间尺度和粒度下进行比较和分析。而不同的数据获取方式直接决定了轨迹数据的时间采样粒度，如采用GPS获取监控目标的位置时，每隔十几秒便可得到一个时空位置信息，因此，本文以轨迹数据的时间采样间隔(Δt)作为最小的时间分析粒度。

在采样时刻Δt对应的点类型可能为P或P′两种，则下一个时间采样时刻2Δt，对应的点类型也可能为P或P′两种，则理论上可以组合4种轨迹线的基本单元：〈P′P〉，〈PP′〉，〈PP〉，〈P′P′〉。如图2所示，轨迹线基本单元对应的时空特征分别为：〈P′P〉表示目标在P′处停留后移动到P；〈PP′〉表示从P移动到P′并停留；〈PP〉表示目标从P移动到P；〈P′P′〉表示目标从停留点P′移动到下一个停留点P′。

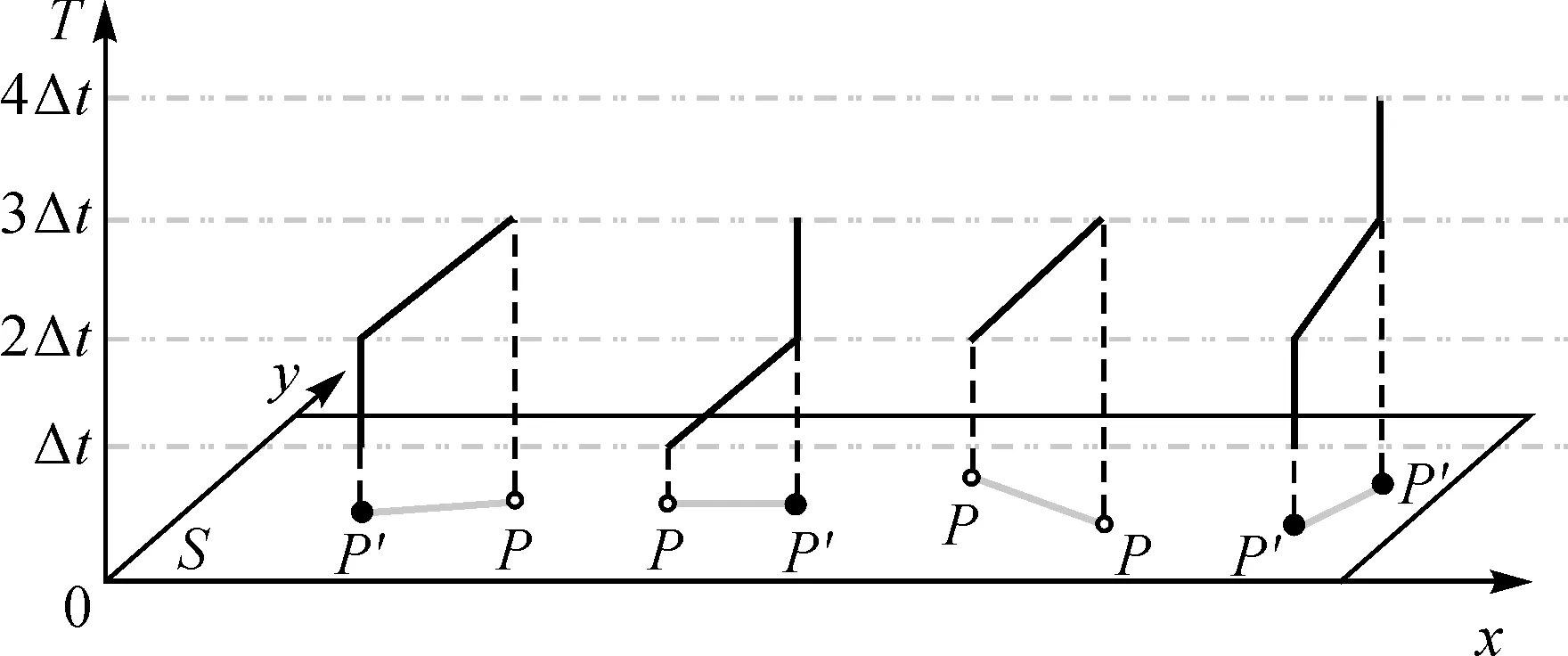
图2 轨迹线的4种基本单元Fig.2 Four basic types of trajectory lines

2 关联出行的轨迹判别与描述

本质上，两条轨迹的时间、空间属性同时存在交集，才会存在时空关联，在此前提下，“等待、接头、同行”等行为蕴含了轨迹之间不同的时空拓扑关系，为此，本节基于点、线时空拓扑关系提出关联出行的轨迹判别与描述方法。

关联出行判别的总体思路可分为3个层次。首先，判断空间交集部分的几何要素类型(Shape(I))，能够区分出公共节点、公共线段两种类型，此为一级规则判别。当交集为点时，进行二级判别：判断公共节点所在原轨迹的轨迹点类型(Type(I))，从而区分出“接头模式”“等待模式”“共处模式”；在此基础上，进行三级判别：判断公共节点部分的时间拓扑关系，进一步对接头、等待、共处3种模式进行细化。当交集为线时，认为出行轨迹存在同行路段，得到“同行模式”，对同行路段的起讫点是否存在等待行为进行二级判别。下文具体介绍关联出行的轨迹三级判别规则及其结果描述。

设犯罪分子A、B，其轨迹线段类型为上述4种基本单元之一。在某时间段n·Δt(n=1,2,…,n)内，SA、SB分别为A、B的空间属性。设I=SA∩SB，I表示A、B的空间交集,当I为非空的情况下：

一级判别规则为：判断I的几何类型，将其记为Shape(I)。

分析可知，4种轨迹线的基本单元相交，其交集的几何类型可能为点或线目标，即Shape(I)∈{Point,Line}。

规则1当Shape(I)=point时，表示A、B轨迹在空间上存在公共点。此时二维平面存在一个公共点I，A、B两目标在I处停留还是移动，决定了二者之间是否存在等待行为，因此，进一步判断Type(I)的类型。

二级判别规则为：判断Type(I)的类型。

将该公共点在A、B中的位置分别记为IA、IB，由轨迹点的类型和特征可知，Type(IA)、Type(IB)的点类型取值均存在两种可能{P、P′}，则其组合可能存在4种情况：{PP,P′P,PP′,P′P′}，其中P′P、PP′顺序无关可归为一种，即Type(I)∈{PP,P′P/PP′,P′P′}。

规则1.1当Type(I)=PP时，即Type(IA)=P且Type(IB)=P，表示“A、B存在交点、且交点所在的原轨迹中均为移动点”，该模式为“接头模式”。

接头模式的判断规则、图示及语义解释见表1，对应的现实意义为A、B在移动中接头，且没有停留。

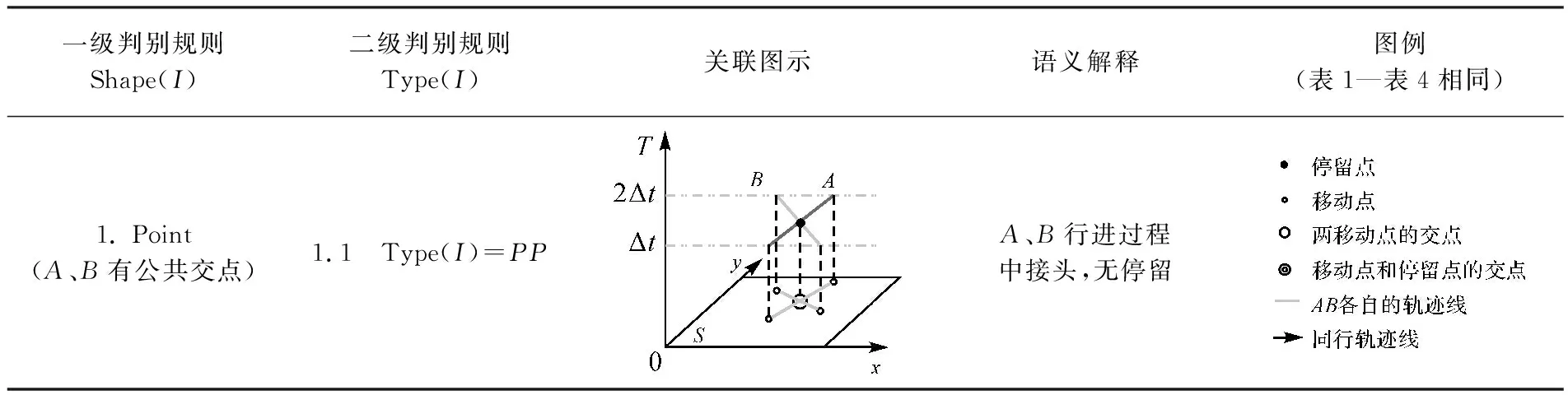
表1 接头模式Tab.1 Meeting pattern

规则1.2当Type(I)=P′P/PP′，即Type(IA)=Pand Type(IB)=P′或Type(IA)=P′ and Type(IB)=P，表示AB存在交点、且交点是一条轨迹的停留点，是另一条的移动点，该模式为“等待模式”。

将交点处的时刻记为T(I)，设等待方的等待时间为T(P′)，交点时间在等待时间中的位置决定了“等待、接头后共同离开”还是“等待、接头后继续停留”等不同的关联行为，为此，需要进一步区分T(I)、T(P′)之间的关系，设时间点和时间线段间的拓扑关系Topology[T(I),T(P′)]。

三级判别规则为：判断Topology[T(I),T(P′)]。

时间轴上，接头时间点T(I)与等待方的时间段T(P′)之间存在3种：点在时间线段起点、点在时间线段终点、点在时间线段中间。

规则1.2.1当T(I)=T(P′).start，表示“接头时间在等待方的时间段起点”。

规则1.2.2当T(I)=T(P′).end，表示“接头时间在等待方的时间段终点”。

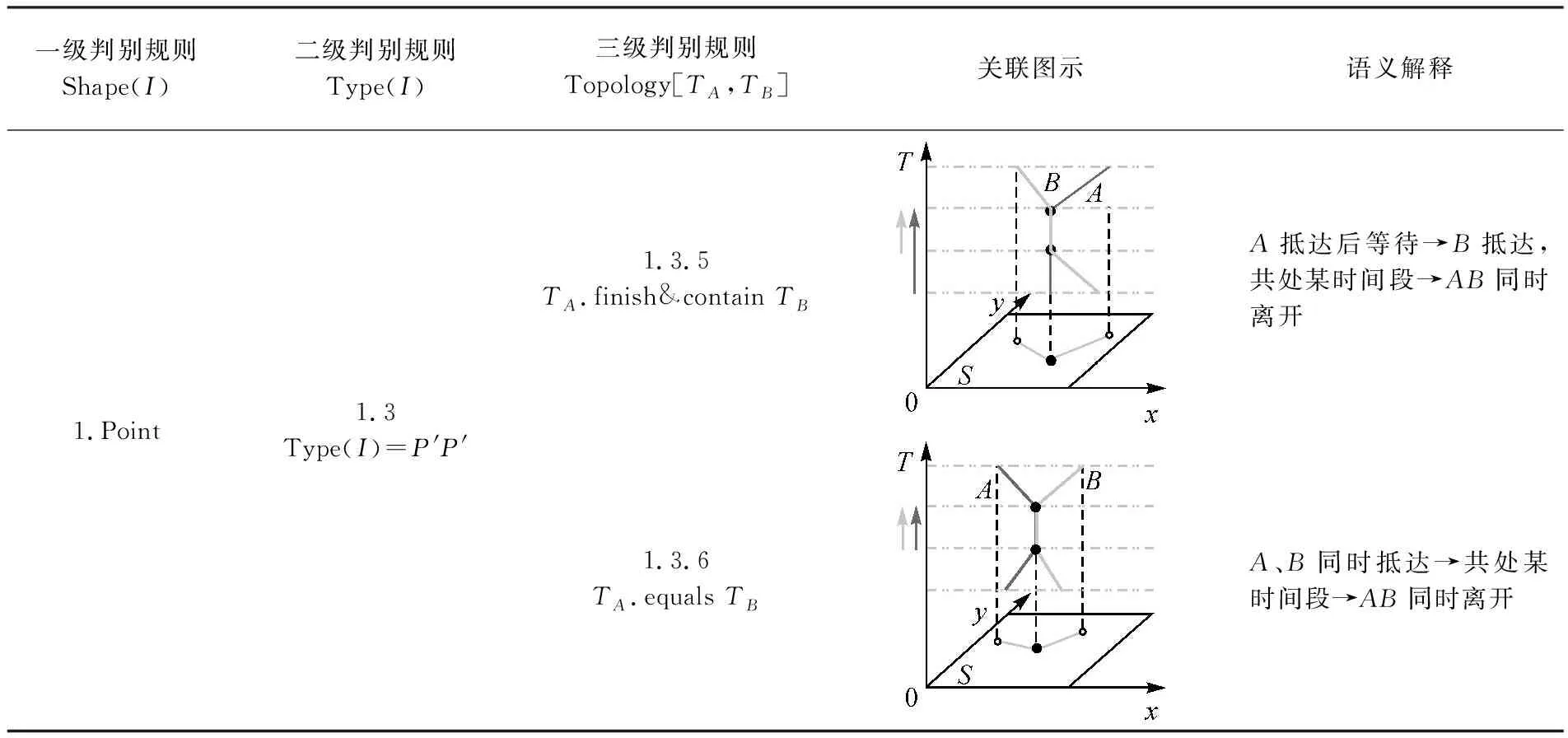
规则1.2.3当T(P′).start

由判别规则1.2.1至1.2.3将等待模式细分为3种子类型，其判断规则、图示及语义解释见表2。

表2 等待模式的细分Tab.2 Subdivision of waiting patterns

规则1.3当Type(I)=P′P′，即Type(IA)=P′ and Type(IB)=P′，表示A、B存在交点、且交点是两条轨迹的停留点，即A、B在各自停留期间在某段时间内共处一地，该模式为“共处模式”。

进一步对共处时间进行区分，可以区分“同时抵达”或者“同时离开”等不同的关联出行类型。将A、B的停留时间分别记为TA、TB，二者为有向时间线段、且存在交集。设Topology[TA,TB]表示A、B的时间拓扑关系，

三级判断规则为：判断Topology[TA,TB]。

根据现有研究[26,27]，选取存在交集的时间拓扑关系共6种：meet、overlap、start&contain、during、finish&contain、equals。

规则1.3.1TA.meetTB，表示“A、B相遇出现”。

规则1.3.2TA.overlapTB，表示“A、B部分同时出现”。

规则1.3.3TA.start&containTB，表示“A、B同时出现且B提前离开”。

规则1.3.4TA.duringTB，表示“A出现期间，B出现并提前离开”。

规则1.3.5TA.finish&containTB，表示“B在A出现过程中出现且同时离开”。

规则1.3.6TA.equalsTB,表示“A、B完全同时出现”。

在上述6种时间关系中，本文关注的是A、B之间的时间关联类型，而不关注A、B的出现顺序，即规则中的A、B顺序可换。如规则1.3.3中，既描述“A、B同时出现且B提前离开”，也能描述“A、B同时出现且A提前离开”。下文规则2也同此。

由判别规则1.3.1至1.3.6将共处模式分为6种子类型，其判断规则、图示及语义解释见表3。

表3 共处模式的细分Tab.3 Subdivision of coexistence patterns

续表3

规则2当Shape(I)=line，表示A、B轨迹在空间上存在公共线段，即A、B在该轨迹线段上同行，称为“同行模式”。

此时二维平面存在公共轨迹线段I，判断I的拓扑特征类型，可以进一步区分“同行起讫点是否存在等待”等主观意图。

二级判别规则为：判断交集线段I的拓扑特征，记为Type(I)。

公共轨迹线段I来自A、B原轨迹，在AB中的轨迹线段类型分别有4种{p′p,pp′,pp,p′p′}，则重叠组合后I的类型可能有16种，去掉与顺序无关的类型，共存在9种公共轨迹线段类型，即Type(I)∈{[P′P′,P′P′],[P′P′,PP],[P′P′,P′P]/[P′P′,PP′],[PP,PP],[PP,P′P′],[PP,P′P]/[PP,PP′],[P′P,PP′]/[PP′,P′P]/[P′P,P′P]/[PP′,PP′],[P′P,P′P′]/[PP′,P′P′],[P′P,PP]/[PP′,PP]}。

规则2.1当Type(I)=[P′P′,P′P′]，表示“A、B共处→同行→共处→分开”。

规则2.2当Type(I)=[P′P′,PP]，表示“A、B共处→同行→分开”。

规则2.3当Type(I)=[P′P′,P′P]/[P′P′,PP′]：表示“A、B共处→同行→A停留B离开”或“A、B共处→同行→A离开B停留”。

规则2.4当Type(I)=[PP,PP]，表示“A、B接头→同行→分开”。

规则2.5当Type(I)=[PP,P′P′]，表示“A、B接头→同行→A、B共处”。

规则2.6当Type(I)=[PP,P′P]/[PP,PP′]，表示“A、B接头→同行→A停留B离开”或“A、B接头→同行→A离开B停留”。

规则2.7当Type(I)=[P′P,PP′]/[PP′,P′P]/[P′P,P′P]/[PP′,PP′]，表示“A等待B→接头后同行→A离开B停留”或“B等待A→接头后同行→A停留B前行”或“A等待B→接头后同行→A停留B前行”或“B等待A→接头后同行→A离开B停留”。

规则2.8当Type(I)=[P′P,P′P′]/[PP′,P′P′]，表示“A等待B→接头后同行→AB共处”或“B等待A→接头后同行→AB共处”。

规则2.9当Type(I)=[P′P,PP]/[PP′,PP]，表示“A等待B→接头后同行→A、B分开前行”或“B等待A→接头后同行→A、B分开前行”。

由判别规则2.1至2.9将同行模式分为9种子类型，其判断规则、图示及语义解释见表4。

综上，基于该三级判别规则，能够区分和描述“接头模式”“等待模式”“共处模式”“同行模式”4种基本的关联出行轨迹模式，并可进一步描述共19种不同的关联出行子类型(表1—表4)。

表4 同行模式的细分Tab.4 Subdivision of companion patterns

一级判别规则Shape(I)二级判别规则Type(I)关联图示语义解释2.Line2.5[PP,P'P']A、B接头后同行→A、B共处→各自分开2.6[PP,P'P]/[PP,PP']A、B接头后同行→A停留B离开/A、B接头后同行→A离开B停留2.7[P'P,PP']/[PP',P'P]/[P'P,P'P]/[PP',PP']A等待B→接头后同行→A离开B停留/B等待A→接头后同行→A停留B前行/A等待B→接头后同行→A停留B前行/B等待A→接头后同行→A离开B停留2.8[P'P,P'P']/[PP',P'P']A等待B→B抵达后同行→AB共处→各自分开前行/B等待A→A抵达后同行→AB共处→各自分开前行2.9[P'P,PP]/[PP',PP]A等待B→接头后同行→到达某地后各自分开前行/B等待A→接头后同行→到达某地后各自分开前行

3 试验与分析

本文采用某案件相关的车辆轨迹数据进行试验。2014年某日凌晨3时左右，某市公安局接到报警：在该市码头有人遭到一伙戴口罩、持棍棒的不明身份人员殴打，作案后违法犯罪嫌疑人员全部逃窜。侦查人员分析嫌疑人很有可能自带交通工具，并发现牌号为皖**车辆在案发时段有过活动轨迹，通过视频监控平台轨迹分析，发现该车在案发当日凌晨3时前后均在中心现场附近出现过，并在多个记录点发现同行嫌疑车辆，但由于车牌号码遮挡，无法区分，因此，需要进行同行车辆分析，以便还原犯罪团伙的作案过程。

提取案发前后1 h内该路段附近摄像头的车辆数据，结合人工判断，提取4辆相关车辆的轨迹。为消除GPS测量误差导致同行模式下的轨迹线偏离，进一步将所有轨迹点匹配到统一的道路线上，并进行数据加密，预处理后的该4辆车的时空轨迹如图3所示。

图3 预处理后的4车辆时空轨迹Fig.3 Spatio-temporal trajectories of the four vehicles after preprocessing

采用文献[12]常见的车辆伴随模式挖掘方法，得到车辆的关联出行模式为共同停留点和同行路段两类，a车与b车在时间段t1共同停留在路口1；a车、b车、c车、d车在时间段t2于隋炀东路同行；a车、b车、c车、d车在时间段t3共同停留在路口2；a车与c车在时间段t4于学士东路同行；b车与d车在时间段t4于隋炀东路同行；a车、b车、c车、d车在时间段t5于瘦西湖路同行；a车与c车在时间段t6于瘦西湖路同行；b车与d车在时间段t6于黄金坝路同行；a车、b车、c车、d车在时间段t7于瘦西湖路同行(表5)。图4为标注结果的地图。

图4 车辆伴随模式分析结果Fig.4 Results of companion pattern mining

表5 文献[12]方法挖掘的车辆伴随模式Tab.5 Companion pattern mining based on reference [12]

采用本文关联出行分析方法，判断四车均存在时空关联，关联出行模式的描述如图5所示。其中，a车与b车的关联类型为：a车在路口1等待b车→b车到达后共处→b车离开→于路口1接头→于隋炀东路同行→于路口2共处→于路口2同行→各自离开→于瘦西湖路接头→各自离开。a车与c车的关联类型为：于路口1接头→于隋炀东路同行→于路口2共处→于路口2同行→于学士东路同行→于瘦西湖路同行。a车与d车的关联类型为：于路口1接头→于隋炀东路同行→于路口2共处→于路口2同行→各自离开→于瘦西湖路接头→各自离开。b车与c车的关联类型为：于路口1接头→于隋炀东路同行→于路口2共处→于路口2同行→各自离开→于瘦西湖路接头→各自离开。b车与d车的关联类型为：于路口1接头→于隋炀东路同行→于路口2共处→于路口2同行→于隋炀东路同行→于瘦西湖路同行→于黄金坝路同行→于瘦西湖路同行。c车与d车的关联类型为：于路口1接头→于隋炀东路同行→于路口2共处→于路口2同行→各自离开→于瘦西湖路接头→各自离开，详细说明见表6。

图5 涉案车辆的关联出行模式类型Fig.5 Types of spatio-temporal association patterns of vehicles involved in the case

相比文献[12]只能区分共同停留点和同行路段2种关联出行类型，本文方法能够进一步区分和描述19种不同的带有碰头、等待等主观意图的关联出行行为，包括共点模式中的“接头模式”“等待模式”“共处模式”3种基本类型，其中，接头模式包含1种子类型、等待模式可细分为3种子类型、共处模式可细分为6种子类型；并能区分和描述共线模式中9种不同的同行子类型。如表5中时间段t1，a车与b车共同停留在路口1，对应表6中可进一步描述为“a车抵达后等待b，共处某时间段后b提前离开”；表5中时间段t2，a车、b车、c车、d车在隋炀东路同行，对应表6中可进一步描述为“a车、b车、c车、d车接头后同行→到达路口2后共处”。相比简单的共点、共线模式，本文方法能够更细致地描述犯罪嫌疑人“接头、等待”等复杂的主观意图，对于案件侦查中还原作案团伙的作案动机、作案轨迹等关键信息具有重要作用。

表6 本文方法挖掘的车辆关联出行模式Tab.6 Association pattern mining based on this paper

其原因在于，现有的轨迹模式挖掘方法是基于轨迹点要素模型，计算时间和空间两个因素的交集，故而只能发现共同的停留点或行驶路线；而本文基于“点-线”特征的出行轨迹描述方法，不仅能对轨迹点的关联类型进行分析计算，也能从轨迹线的角度，分析点与线、线与线之间的时空拓扑关系，从而能够区分等待、接头等更多的关联出行类型。

4 结 论

本文针对现有的共点、共线描述方法无法区分更多的犯罪关联模式，首先提出了顾及“点-线”特征的出行轨迹描述方法，能够较好地兼顾轨迹的细节点特征和完整线特征；然后，在此基础上，基于时空拓扑关系提出了关联出行轨迹的三级判别方法，能够描述“接头”“等待”“共处”“同行”4种基本的关联出行轨迹模式，并可进一步细分为19种更详细的子类型。基于这些出行轨迹关联模式，能够在时空背景下解析人员复杂的互动关联，对犯罪防控、案件侦查等有重要的帮助意义，并可为时空关联分析、时空行为建模等提供思路和方法。