实验室冲击响应谱比对参数识别技术研究
2022-09-01舒礼邦陈东东张静
舒礼邦 , 陈东东 , 张静
(1.中国电子科技集团公司第五十五研究所, 江苏 南京 210000;2.南京奥马微波光电产品检测中心有限公司, 江苏 南京 210000)
0 引言
传统冲击试验采用的是典型冲击脉冲模拟冲击环境, 没有考虑实际冲击响应的损伤效果, 而冲击响应谱通过冲击响应来模拟冲击效果, 对实际冲击环境的模拟更加真实[1]。 冲击加速度峰值和拐点频率是准确评估冲击响应谱的模拟效果的关键物理量。 为了提高时域加速度峰值的比对精度, 需要合理地选择数字信号采集系统中低通滤波器的截止频率。 在JJG 541—2005、 GJB 150.16 等冲击标准中仅仅给出了经典冲击波形测量系统滤波截止频率,例如: JJG 541—2005 《落体式冲击试验台》 中给出了18 ms 脉宽冲击的滤波截止频率为2 kHz;GJB 360A—96 《电子及电气元件试验方法 方法213 冲击试验》 中是11 ms 对应2 kHz; GB/T 2423.5—1995 《电工电子产品环境试验 第2 部分: 试验Ea和导则: 冲击》 中则是30 ms 对应2 kHz。 冲击响应谱的波形一般为复杂震荡衰减波形, 加速度值时域历程基本在20~30 ms 衰减为0; 2 kHz 的频率上限适用于经典冲击脉冲系统频率特性上限, 经典冲击脉冲通过这样的频率特性测试系统, 其冲击脉冲的真实加速度值被很好地保留, 但是对于复杂瞬态波形来说, 其中还有很多代表真实加速度值的高频分量, 测试系统频率特性上限(2 kHz) 偏低。
目前不同的标准中均没有给出冲击响应谱试验中低通滤波器的截止频率。 学者张建华[2]的相关研究成果指出冲击响应谱时域的时间历程, 其滤波截止频率设定为最高信号频率的1.5 倍, 爆炸冲击加速度时间历程的主要频率范围为1×102~1×106Hz。 学者唐林[3]建议将低通截止频率设定为10 kHz, 而且频率越低加速度有效值越低, 波形损失细节也越多。 研究成果表明, 不同的滤波频率会影响冲击响应谱时域加速度峰值的准确性, 所以工程应用中常常根据工程经验给出相对宽泛的低通截止频率范围, 该结论虽然可以指导比对试验,但没有像经典冲击试验规范中将表征时间加速度历程的脉宽信息, 用于指导滤波频率的选择。 GJB 150.18 附录C 中定义了表征复杂波形时域特征的有效持续时间(τE和τe), 该时间由冲击包络初始上升段和结尾下降段拟合而成, 包含了冲击响应时域的最大值, 代表了复杂冲击时间历程重要的频率信息, 并且τE和τe之间建立了统计模型, 统计结果适用于各种复杂冲击响应环境模拟。 而对应冲击响应谱的拐点识别, 一般采用极值法识别, 其识别准确性受到冲击效果一致性好坏、 冲响设备和样品耦合后的动力学特性等因素的影响, 目前国内对如何提高冲击响应谱拐点识别精度的报道较少。 国外学者Yan Yinzhong[4]提出, 通过优化不同频率的低通滤波频带宽度, 保障各个谐波均在同一时刻达到最大值后, 对冲击响应谱进行叠加, 并给出最大滤波截止频率(38.4 kHz), 以保障叠加后冲响谱各个拐点的准确性。
因此, 在冲击响应谱试验中, 尝试通过建立低通截止频率数学模型和拐点频率识别数学模型, 为早日建立起统一的识别冲击加速度峰值和拐点频率的标准方法提供一种思路。
1 冲击响应谱的原理和比对规范
1.1 冲击响应谱的原理
爆炸冲击是一种确定性、 非周期性瞬态振动。爆炸冲击环境的特点是: 高频值的震荡波形, 持续时间很短, 一般在20 ms 内衰减到零。 这种爆炸冲击特性一般用冲击响应谱来表征。
冲击响应谱是指将冲击源施加于一系列单自由度、 线性且无质量弹簧振子, 将各自单自由度振子的响应运动中的响应峰值, 作为对应结构固有频率的函数, 即定义为冲击响应谱[5]。 可见冲击响应谱表征的是线性单自由度系统固有频率与受到冲击时所产生的响应峰值之间的关系。 冲击响应谱不包含激励与响应之间的相位信息, 因此不同的冲击时域波形可以有相同的冲击响应谱[6]。
1.2 比对试验规范和样品装夹
客户A 和客户B 进行冲击响应谱比对试验,试验规范如表1 所示。
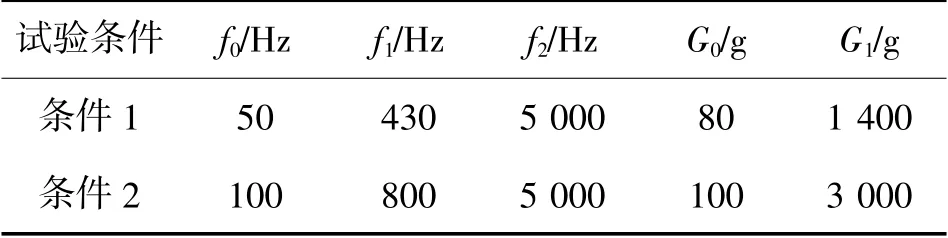
表1 冲击响应谱比对试验规范
冲击响应谱比对试验要求如下所述。
1) 阻尼比: 0.05 (品质因子Q=10);
2) 次数: 每向冲击3 次;
3) 分析频率间隔: 1/12 倍频程;
4) 传感器安装位置如图1 所示;
5) 以1/12 倍频程计算的冲击响应谱允差在-6~+6 dB 范围, 应保证至少50%的冲击响应谱幅值超过规定的试验值。
客户A 和客户B 均采用同一“L” 形铝板, 该铝板具有丰富的共振频率, 并按照GB/T 2423.43—2008 《电工电子产品环境试验 第2 部分: 试验方法 振动、 冲击和类似动力学试验样品的安装》中所描述要求完成固定, 实际样品的装夹图如图1所示。

图1 客户B 冲响装夹图
2 冲击响应谱比对的限制条件
当冲击谱模拟试验所采用的加速度时间历程曲线与实际相差很大时, 模拟试验或者说比对试验仍然存在过试验或欠试验的可能, 可见对于冲击响应谱的比对中, 对加速度时间历程曲线应提出下列限制:
1) 试验的加速度时间历程要尽量地接近外场或另外一家比对客户所测得时间历程, 尤其是要求峰值相近;
2) 试验的加速度持续时间尽量地接近外场或另外一家比对客户所测数据的持续时间, 或者在统计上要占绝大多数;
3) 试验的放大系数与实际放大系数相近;
4) 尽量使试验冲击谱与外场冲击谱的一致性能同时满足两种结构阻尼状态[7]。
由此可见, 要完成实验室间冲响试验比对, 其限制条件还是比较严苛的。 不仅要求结构阻尼状态不一样的两家单位的设备, 其冲击响应谱一致性满足比对要求, 特别要求加速度时间历程中的峰值接近, 而且在冲击谱中还要满足冲击谱规范, 例如:拐点要求、 容差要求等信息; 另外, 比对中应尽可能地限制冲击响应谱的激发类型, 因为不同的激发类型时域波形特性不同, 会导致时域时间历程中的加速度峰值存在较大差异, 而相同类型冲击响应谱设备的激发类型一样, 时域波形相似程度较高[8]。
3 低通滤波截止频率模型
3.1 冲击响应谱有效持续时间(τE 和τe)
按照国军标GJB 150.18—2009 冲击试验中的描述, 冲击响应谱的有效冲击持续时间有τE和τe两种。
有效持续时间τE是包含绝对值超过1/3 最大峰值Ap的所有时间历程幅值所对应的最小时间的长度; 有效持续时间τe(对处理复杂瞬态数据更合适) 是指包含至少90%以上的均方根(RMS) 时间历程幅值超过最大均方根幅值10%的时间历程所对应的最小时间长度。 τE代表了复杂波形的时域特征, 从定义中可知, 只要测得完整的时域加速度历程即可得到τE的值。 而τe则更具备复杂波形时域特征的统计意义, 更能代表复杂冲击响应谱的加速度时间历程的时域特征。 这两个持续时间从统计模拟中可知道τe~τE之比的中间值为2.62, 而且有95%的比值落在1.71 和5.43 之间, 一般τe近似地为τE的2.5 倍[9]。
在GJB 150.18A—2009 附录C.3.3 冲击分析与τe的关系中给出了τe>1/2fmin, 其中fmin是冲击响应谱分析的最低频率, 假设一个复杂冲击大约在30 ms 内衰减到零, 而TE假设为20 ms, 按照该关系式fmin>10 Hz, GJB 150.18A—2009 给出了低通滤波截止频率的下限值, 低通截止频率的上限值并未明确说明。 而低通滤波器的频率上限最小值, 应能保留复杂瞬态冲击波形的峰值加速度, 滤除加速度计谐振等高频干扰项[10]。
3.2 数学模型推导
将非周期函数的复杂冲击波形定义为f (t),则傅里叶变换频谱为:
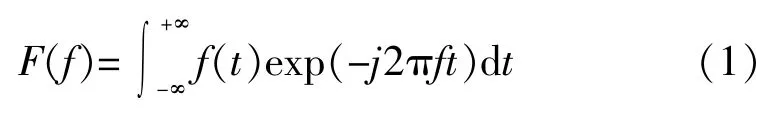
其傅里叶变换的逆变换为:
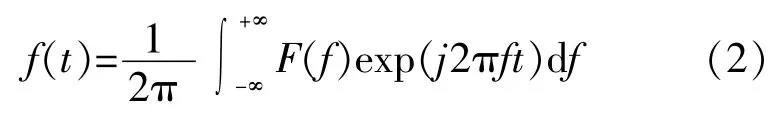
从傅里叶逆变换式(2) 中可看出, 复杂波形f(t)表征为不同频率分量的线性叠加, 而每一个叠加的分量为F (f)exp (j2πft)f∈[-∞, +∞]。 这里假设复数F (f)的初始相位为零, 则分量表达式化简为:
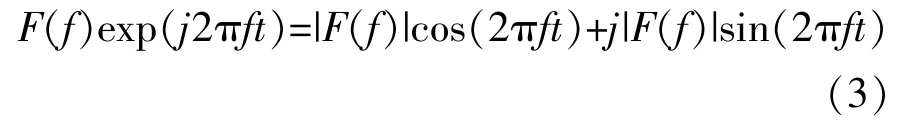
在《振动与冲击手册》 中, 标准半正弦波表达式[11]为:
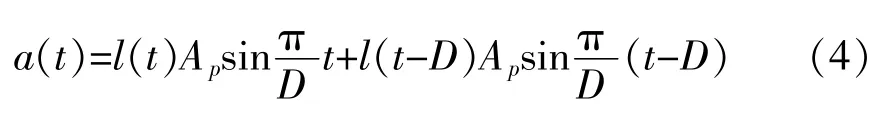
式(4) 中: D——半正弦波脉宽;
l (t) ——单位阶跃函数。
对应的频谱幅值表达式为:
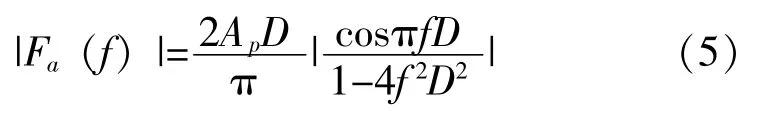
式(3) 中的正余弦函数可用以上标准半正弦波来表示:
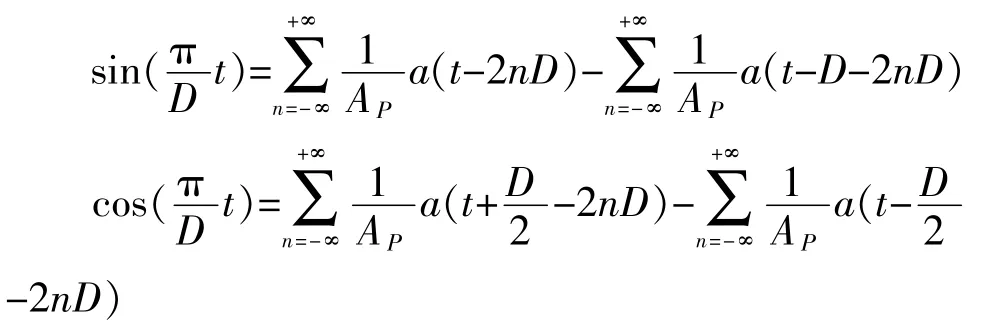
其中, 正余弦函数的频率f 和半正弦波脉宽D关系为2Df=1。 F(f)exp(j2πft)可用标准半正弦波的线性叠加来表示, 即:
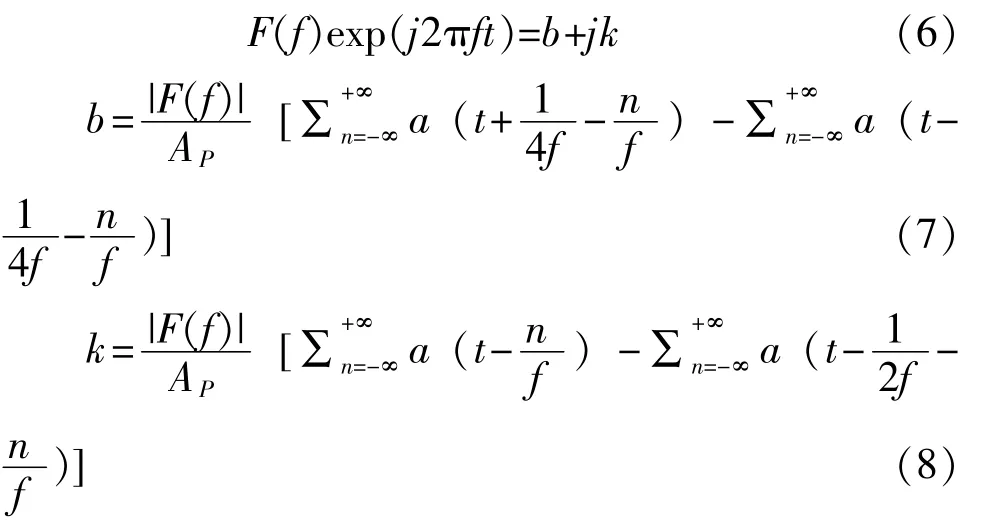
从式(2) 傅里叶逆变换物理意义出发, 复杂波形f (t) 是每个分量F (f) exp (j2πft) 的线性组合, 而每个分量F (f) exp (j2πft) 又是无数个脉宽为1/2f 的半正弦波线性组合, 而半正弦波的时域波形和频率幅值如图2 所示。
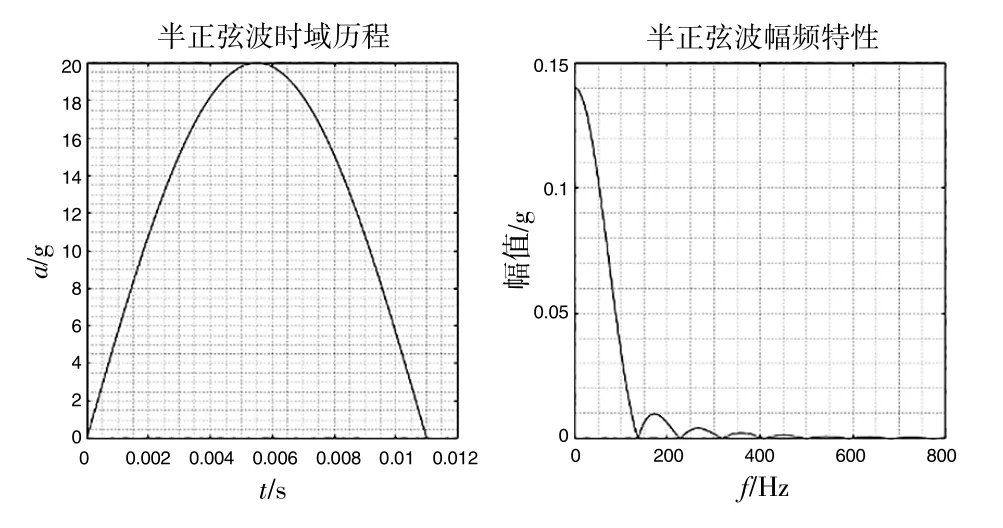
图2 半正弦波波形和傅里叶谱
根据傅里叶变换的线性性质, 复杂波形的傅里叶谱可用无数个半正弦波频谱的线性组合来表达,每个分量F (f) exp (j2πft) 的频谱均为a (t) 频谱的线性叠加。 不同频率f 对应的权重|F (f) |/Ap决定了对复杂波形频谱贡献大小。 而要准确地测得复杂波形的时域加速度峰值, 低通滤波器的频率上限应至少满足图2 中半正弦波幅频曲线第一个幅值为零的频率, 而从式(5) 中可知, f=3/2D、 f=5/2D、 f=7/2D…分别对应第一、 第二、 第三幅值为零的频率值, 故滤波频率上限可合理地假设为:
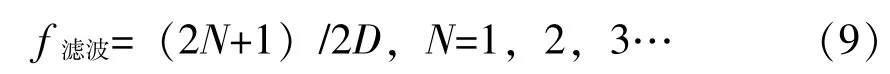
D 值反映的是半正弦波脉宽, 而τe从统计意义上反映的是复杂波形的脉宽, 两种物理含义接近, 所以复杂波形冲击响应谱的滤波频率上限估计为:
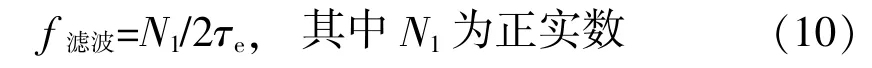
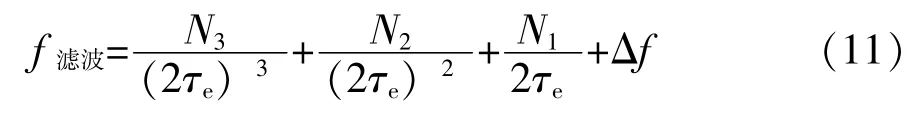
3.3 数学模型参数估计方法
式(11) 中涉及到4 个待求参数, 即N3、 N2、N1、 Δf, 这里采用最小二乘法对4 个参数进行估计。
最小二乘法的原理是将试验所测数据项建立多组线性回归方程组, 通过构建测量数据结果的残差项平方和, 最小二乘法参数拟合出模型函数中的关键系数值, 一般回归方程组形式如下:
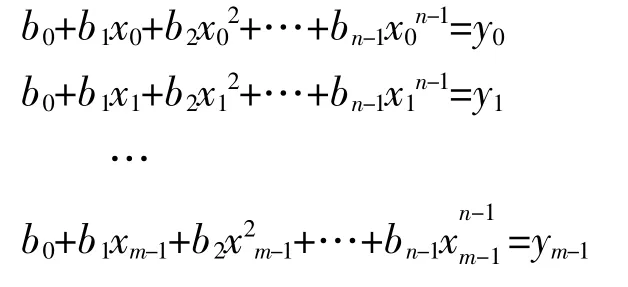
对应的输入测试数据矩阵A∈Rm×n、 待求系数矩阵b∈Rn、 输出测试数据矩阵y∈Rm如下:

且yTAb= (yTAb)T, 是因为该矩阵乘积最终为一有理数, 最小化Φ (b) 等价于:
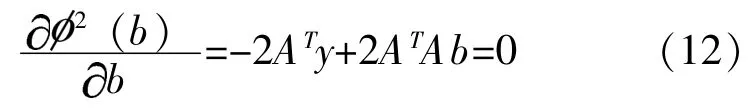
在正规方程组ATAb=ATy 中, 左乘(ATA)-1,可解出系数向量b。
3.4 试验数据和分析
客户A 和客户B 两家单位的测试数据要满足第2 节中限制条件的要求, 从装夹图1 中可以看出客户A 和客户B 均有5 个测试点, 每个测试点连续冲击3 次, 要完成1 400 g 和3 000 g 两组条件。两家单位3 号测点的加速度时域波形比较情况如图3-4 所示。
从图3-4 中可以看出, 客户A 和客户B 不管是1 400 g 还是3 000 g, 相应测试点的加速度时域历程和峰值基本一致, 满足比对限制条件1 和2。对于各个测点的放大倍数如图5 所示。
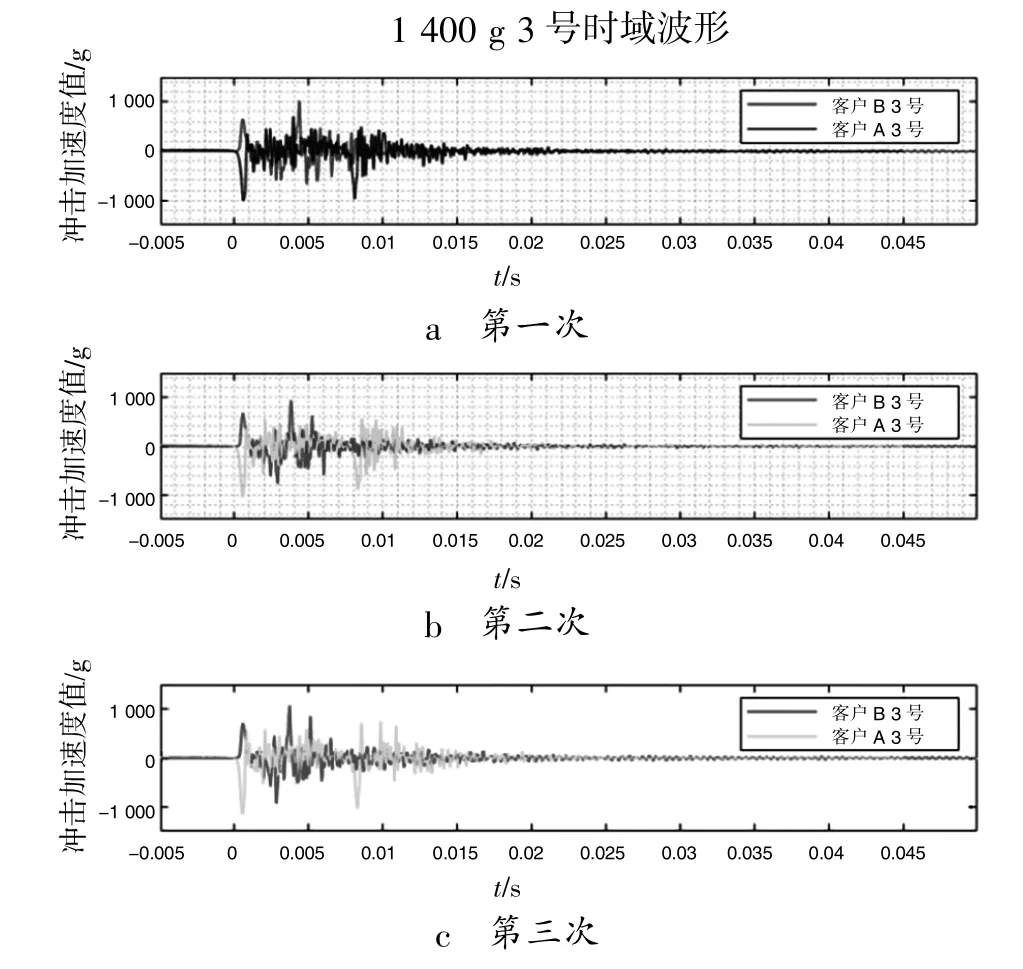
图3 客户A 和B 1 400 g 3 次冲击时域历程
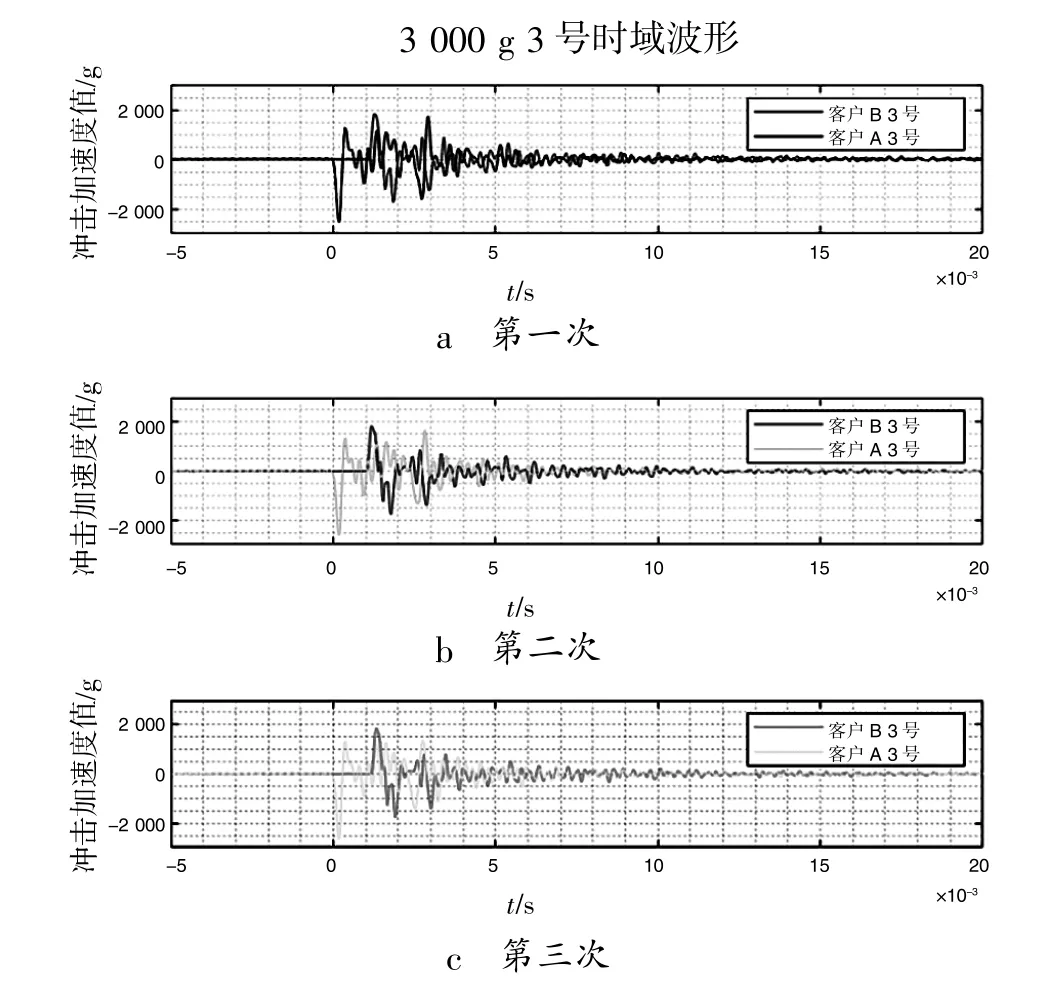
图4 客户A 和B 3 000 g 3 次冲击时域历程
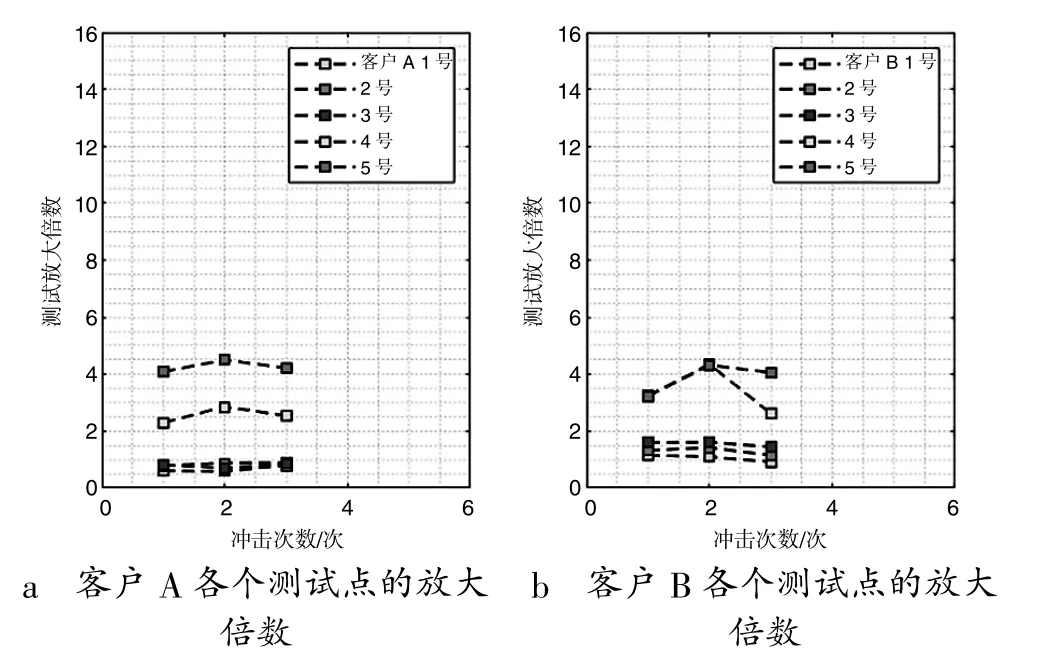
图5 客户A 和B 各个测点的放大倍数
从图5 中可见, 客户A 的1 号、 2 号、 3 号点时域加速度峰放大倍数在0.6~0.9 倍之间, 而客户B 对应点放大倍数在0.9~1.5 倍之间, 两者相差不大。 而客户A 的4 号点放大倍数为2.3~2.8 倍, 客户B 的为2.6~4.3 倍。 客户A 的5 号点放大倍数为4.0~4.5 倍, 客户B 的为3.2~4.3 倍, 也是基本接近的。 而且, 由于4 号和5 号点为响应点, 所以放大倍数相比较1、 2、 3 号点大, 4 号点和5 号点由于位置不同, 所以放大倍数也略有不同, 但均满足了限制条件3 的要求。 最终从客户A 和客户B 处共测得30 个数据, 计算所得τe如图6 所示。
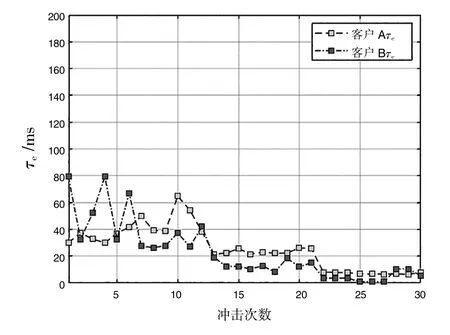
图6 冲响的有效持续时间τe
图6 中前12 对数据为4 号、 5 号点响应测试数据, 后18 对为1、 2、 3 号的激励测试数据。 由图6 可以看出客户A 和客户B 激励点的τe基本一致, 这是因为激励冲响曲线均在规定的比对谱线容差内; 而响应点τe之间的离散较大, 是因为两家单位设备谐振板和L 板组成系统的阻尼状态即使相近, 其A 和B 的τe也会随着冲击次数的增加逐渐地呈现出更明显的离散特性。 该离散特性可以通过增加更多的冲击次数, 获得更多的试验数据从统计意义上进行概括。
将图6 中的测试数据构建成最小二乘法中的输入数据矩阵。 滤波截止频率数据选择那些保证两家单位加速度值在比对允差范围内所对应的滤波频率, 该频率值必须保留频谱中绝大部分的有效值。试验数据代入拟合, 最小二乘法参数拟合结果如图7 所示。
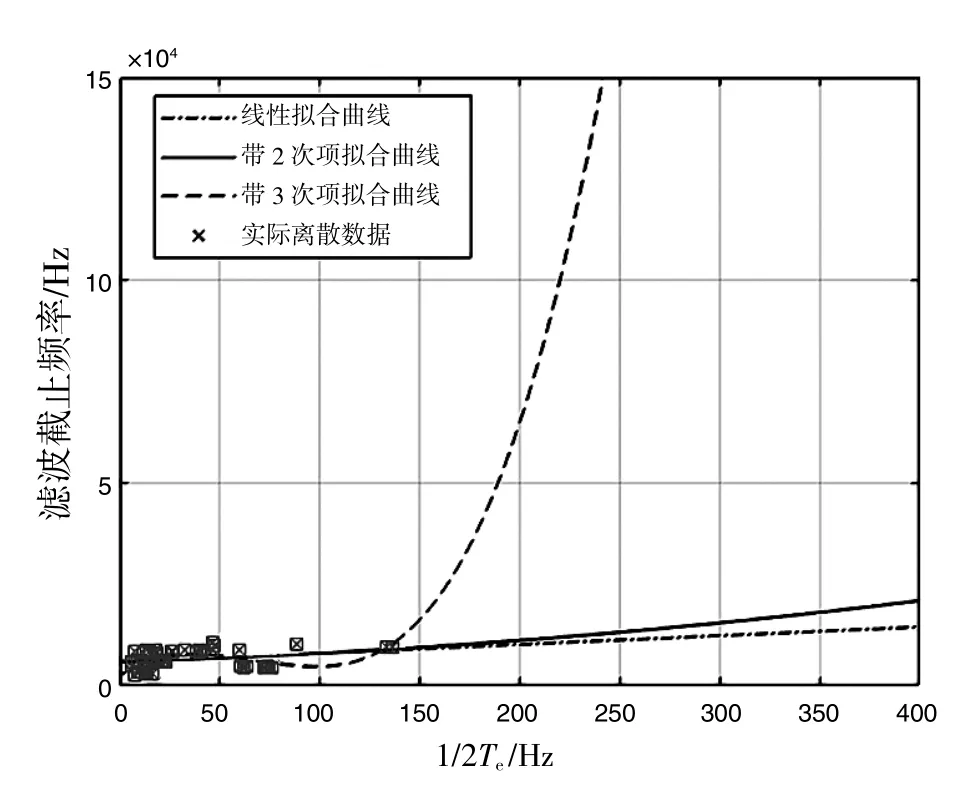
图7 最小二乘拟合曲线
数值分析出低通截止频率的线性项、 二次项和三次项的估计表达式:

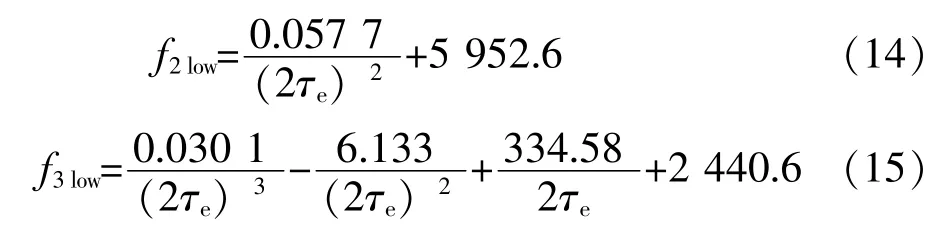
比较3 个低通截止频率估计表达式, 二次项表达式(14) 和实际数据更为接近, 可作为冲响低通滤波截止频率上限的估计。
4 冲击响应谱传递率模型
冲击响应谱的求解主要由计算机完成, 常用的计算方法有Fourier 变换法, 这种方法的思路是将冲击信号进行Fourier 变换(采用快速Fourier 算法), 然后乘以单自由度系统的频响函数, 再对乘积求解逆FFT, 从而得到时域响应, 最后经峰值检测得到冲击响应谱; 而对于有的结构, 监测点处的冲击响应谱拐点可能不止一个[12]。
4.1 数学模型推导
这里先建立冲击响应谱(SRS) 绝对加速度模型。 图8 给出了一个典型的基础激励的机械振动冲击系统, 即一个质量为m, 弹性系数为k, 阻尼为c 的单自由度(SDOF) 系统。 系统输入为基础激励加速度, 输出为质量块加速度值, 这种模型是最常用于冲击响应谱计算的模型。
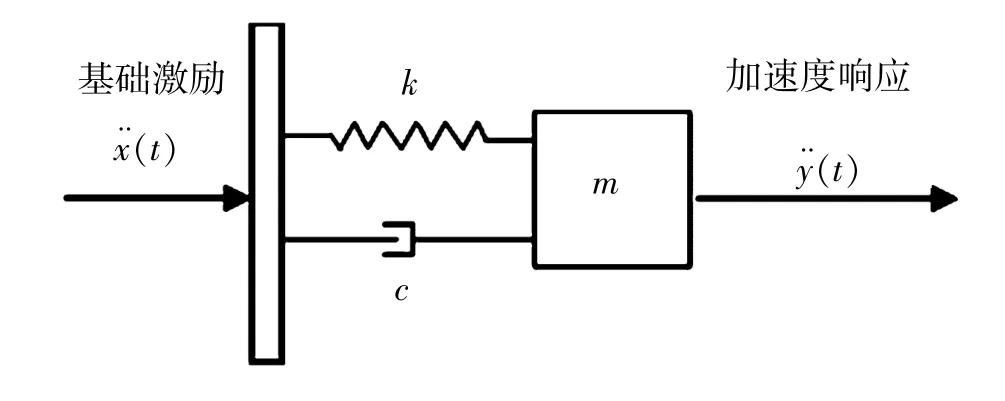
图8 SRS 基础激励冲击系统
通过模型并运用牛顿第二定律列出运动方程式为:

两边取拉式变换, 并利用拉式变换的微分性质可得:
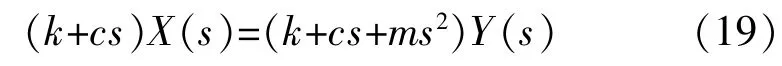
系统复数域拉普拉斯传递函数可写成:
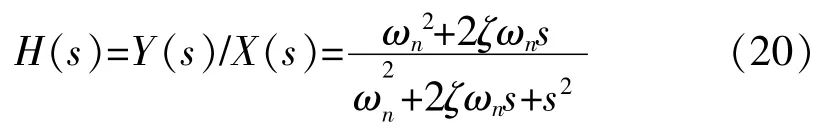
这里假定一函数h (t), 其傅里叶变换和拉普拉斯变换分别为Hf和Hs, 由简单数学关系可知拉普拉斯变换和傅里叶变换之间关系Hf(s/j)= Hs(s),可得傅里叶变换的传递函数为:
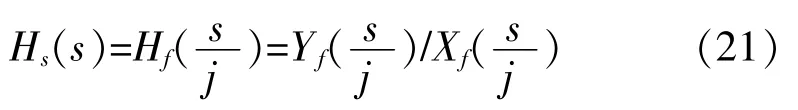
因此一个线性、 单自由度质量弹簧系统的传递函数可以用傅里叶谱表示。
冲击响应谱的物理含义是将冲击源加载到一系列线性、 单自由度质量-弹簧系统上时, 各个单自由度系统的响应运动最大响应值, 作为各个单自由系统固有频率的函数而绘制的曲线。 数学含义则是对不同固有频率fn的单自由度系统, 对其傅里叶谱求逆变换, 并检测出最大峰值或最小峰值作为纵坐标, 以fn为横坐标所绘制的曲线如图9 所示。

图9 冲击响应谱物理含义
令对傅里叶谱求逆变换, 再求最大峰值或最小峰值的函数记作。 冲击响应谱的倍频程大小将系统分解为共振频率为f1、 f2…fn的n 个单自由度质量-弹性系统, 且fn=Sn/j, 则
响应点冲击响应谱:
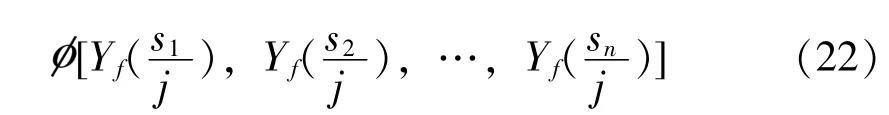
激励点冲击响应谱:
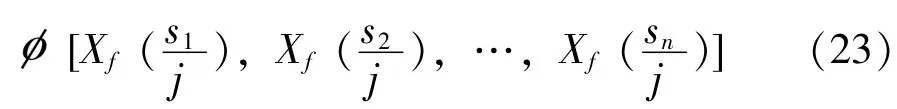
冲击响应谱传递率:
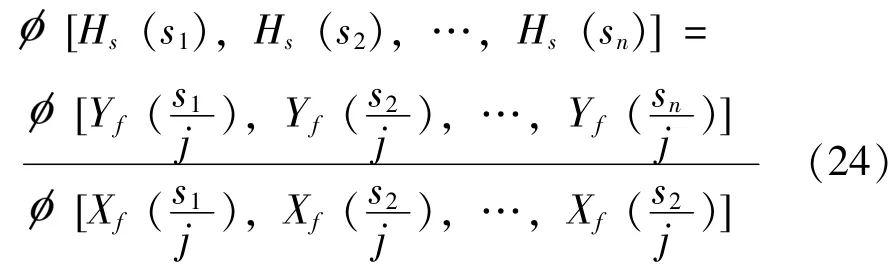
式(22) 中构成一组向量:

该向量代表了激励信号各个单自由度系统的傅里叶变换谱, 但仅用谐振板上一点的激励信号无法完整地表述整个谐振板的激励特性。
这里将样件位置周围谐振板上的1、 2、 3 号各点激励信号分解为一系列共振频率的单自由度系统响应的傅里叶谱, 并构成3 组向量, 即:
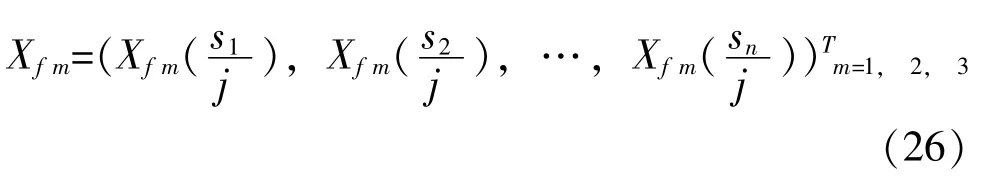
再定义一系列子向量, 即:
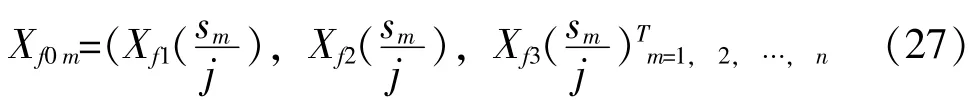
则由向量L2-范数的定义可知:

其中, ρ 为权函数, 并认为该范数等于式(25) 向量中相应元素的取值, 式(25) 可化为:
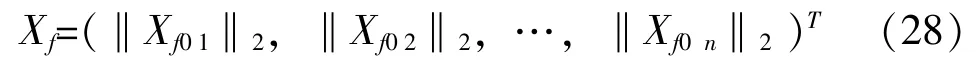
各个子向量2 范数可以表征整个谐振板上一系列单自由度质量-弹簧系统的傅里叶谱, 对式(28) 施加函数, 即可求出表征整体谐振板的冲击响应谱激励谱, 即:

为了能求解出冲击响应谱激励谱式(29) 的值, 定义1、 2、 3 号的冲击响应谱激励谱值m 为:1, 2, 3

并将1、 2、 3 号冲击响应谱构成一个向量式:
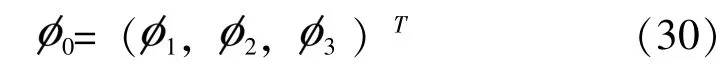
并认为下式成立, 即:
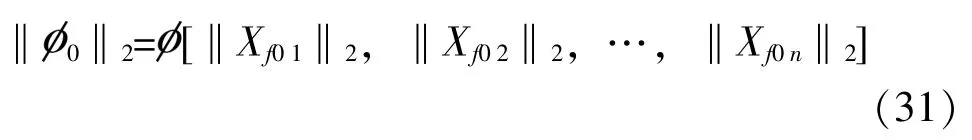
式(30) 可以从测试数据中得到, 最终冲击响应谱传递率可化简为:
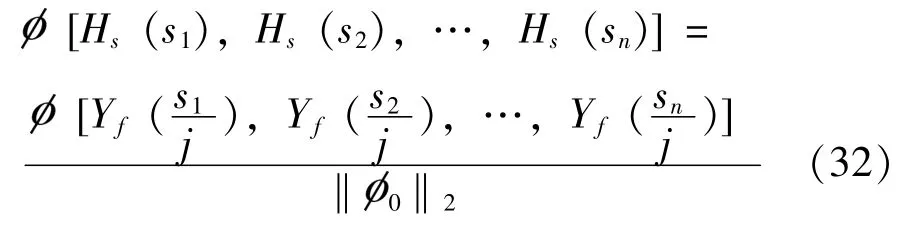
4.2 试验数据和分析
图1 中谐振板上点1、 2、 3 为3 个控制点, 其中点1 和点2 位置靠近谐振板与锤头撞击面, 点3远离撞击面, 位置在谐振板的末端。 点4、 5 为“L” 上不同位置的监测点。 用数采分别采集到客户A 和B 的点1 到点5 冲击响应谱数据, 而由式(31) 可计算出客户A 和客户B 冲响激励谱, 如图10 所示。
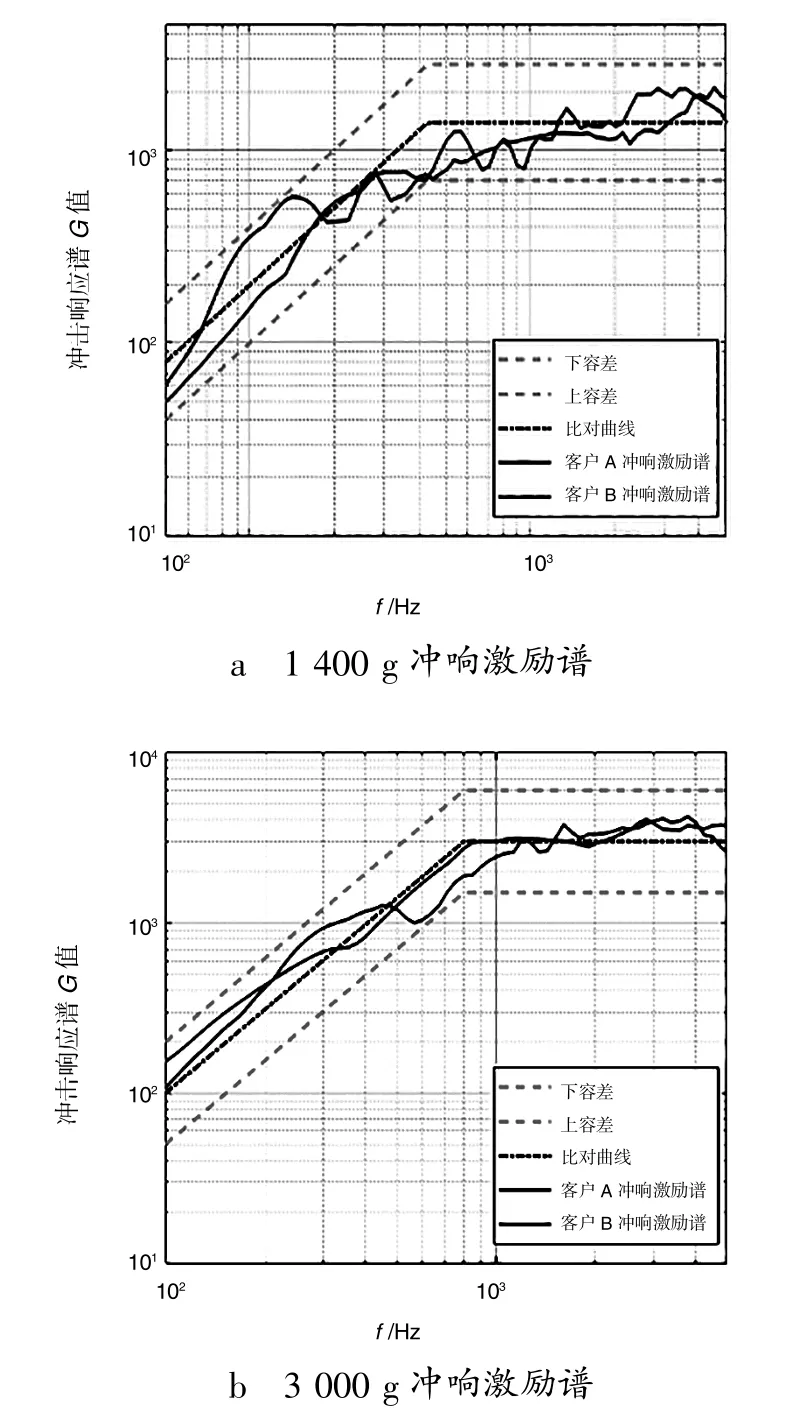
图10 冲击响应激励谱
而从客户A 和客户B 谐振板上分别采集到的监测点4 和点5 冲响响应谱如图11-12 所示。

图11 1 400 g 点4 冲击响应谱
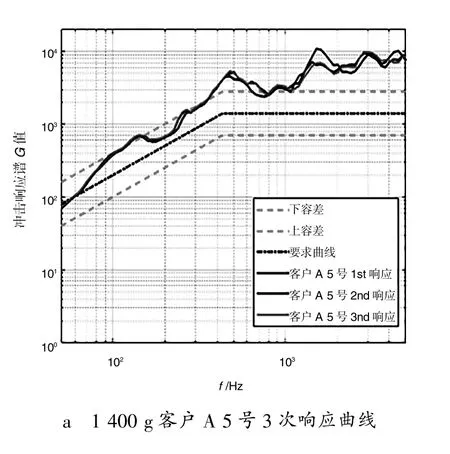
从图11 中可见, 客户A 和客户B 的点4 冲击响应谱的拐点并不明显, 特别是客户A 的谱型基本为一斜线。 而对于图12 客户A 和客户B 的点5冲击响应谱, 能辨识出1 000 Hz 以下的拐点, 但对于1 000 Hz 以上的拐点识别精度不高。
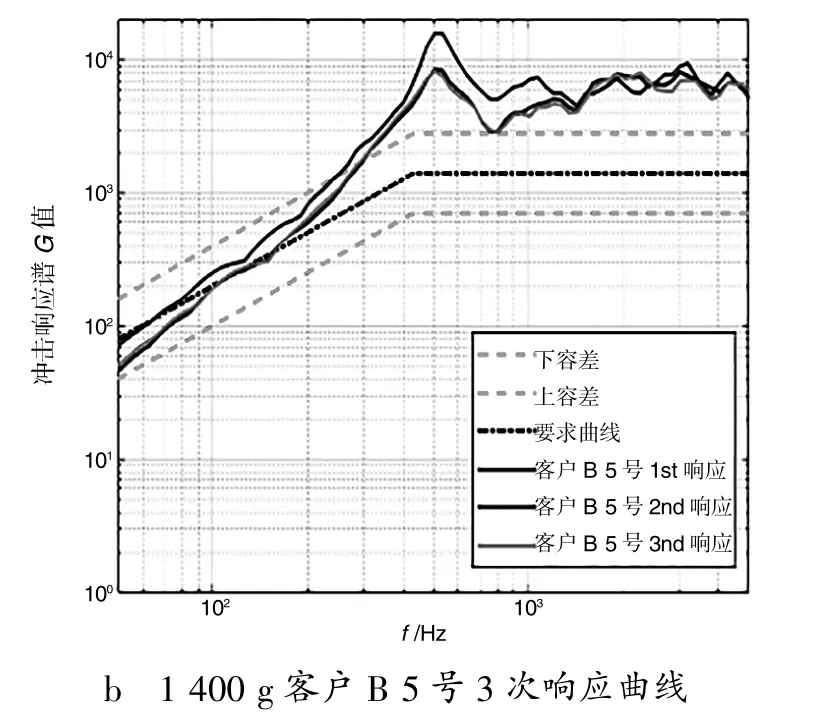
图12 1 400 g 点5 冲击响应谱
利用式(32) 可分别计算出客户A 和客户B点4 和点5 的冲击响应谱传递率函数, 如图13-14所示。
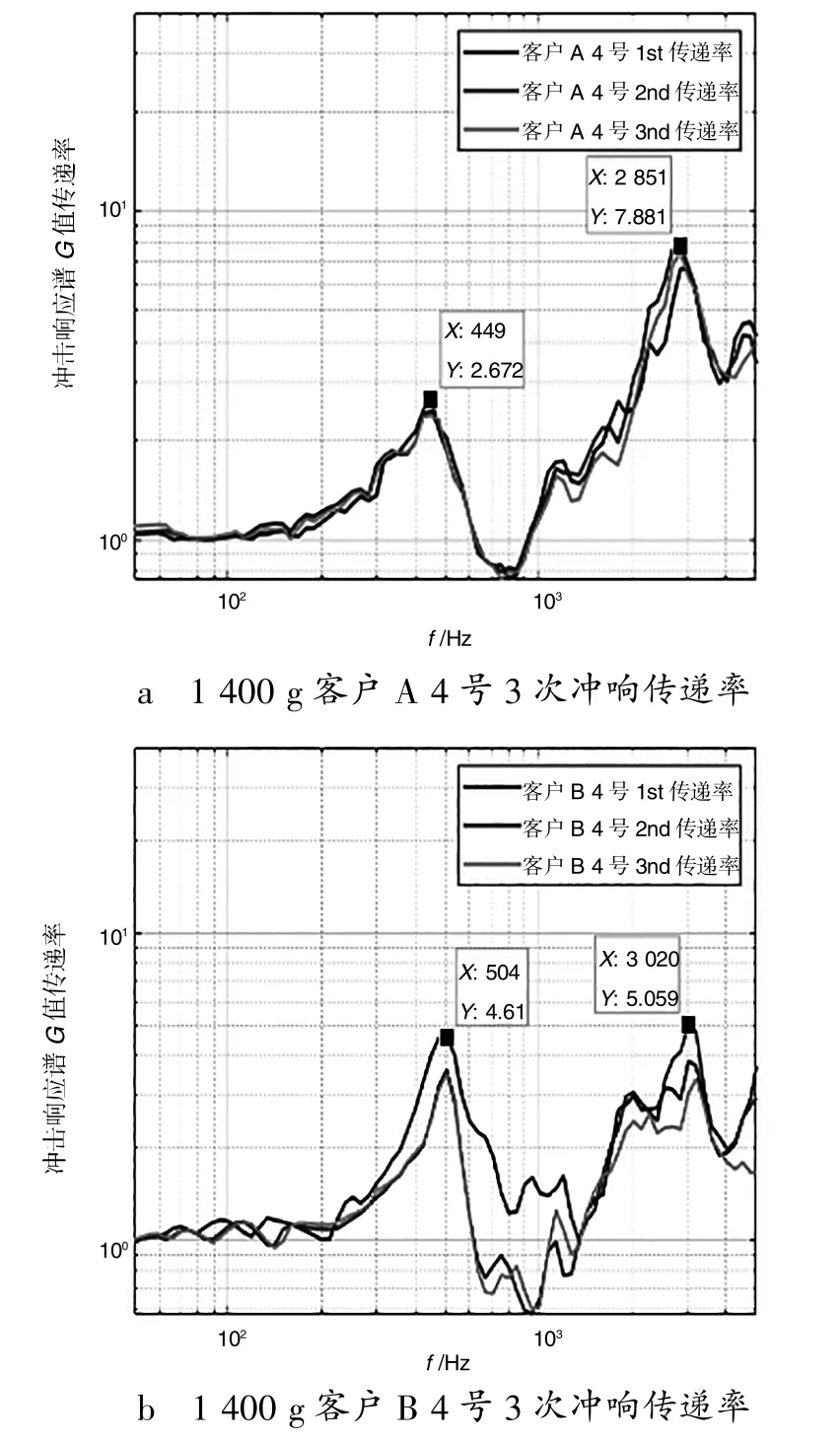
图13 1 400 g 点4 冲击响应传递率

图14 1 400 g 点5 冲击响应传递率
从图13-14 中可以看出, 传递率函数可以放大拐点频率, 使拐点频率更尖锐, 更容易辨识。 这里将1 400 g 和3 000 g 两个条件下, 客户A 和客户B 利用冲击响应传递率所得到的拐点比对结果如表2-3 所示。
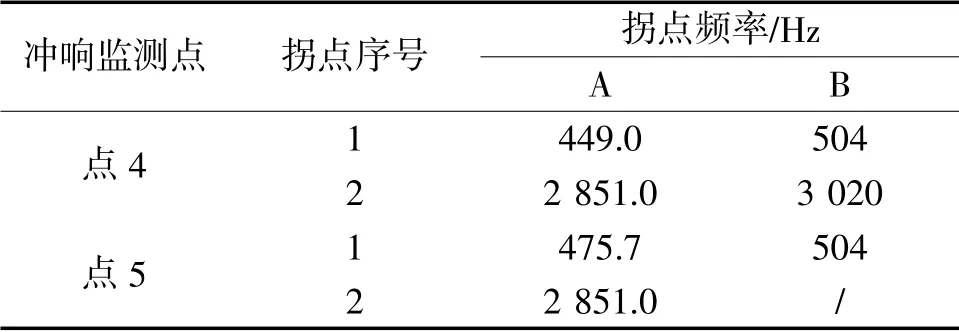
表2 1 400 g 客户A 和客户B 冲响拐点比对结果
从表2 中可以看出, 1 400 g 量级比对下, 客户A 点4 的两个拐点和客户B 的两个拐点值相差不大, 低频误差为12.24%, 高频误差为5.93%。而客户B 折点5 只有一个拐点, 客户A 则有两个拐点, 第一个拐点的误差为5.95%。
从表3 中可以看出, 3 000 g 量级比对下, 客户A 点4 的两个拐点频率值和客户B 的十分接近,仅高频拐点误差为12.22.%。 客户A 点5 有3 个拐点, 和客户B 的也十分接近, 后两个拐点误差仅为5.96%、 12.24%。
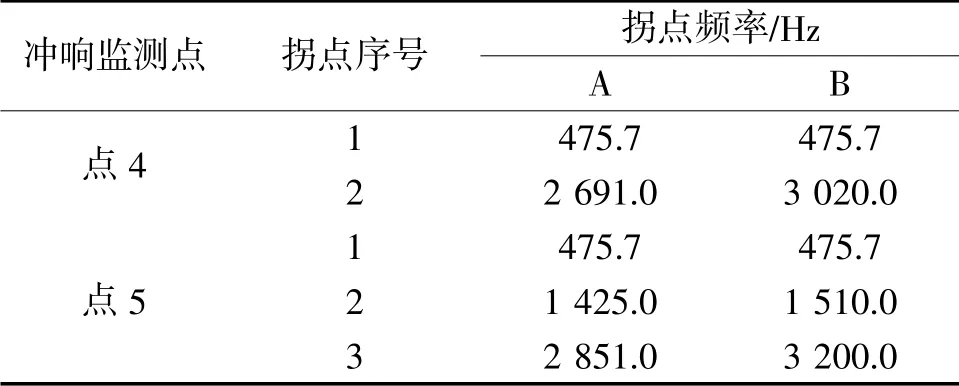
表3 3 000 g 客户A 和客户B 冲响拐点比对结果
5 结束语
如果两家比对单位设备不满足冲响比对试验的限制条件, 即使采用冲响低通滤波截止频率模型设置滤波频率上限, 所求得的加速度峰值仍然存在较大的误差。
冲击响应谱曲线中包括了缓冲区、 放大区和等冲区, 冲击响应谱传递率模型将冲响的响应谱缓冲区、 放大区和等冲区除以冲响激励谱的对应区域,最大程度地还原出响应谱中拐点频率和放大倍数,相比直接从冲击响应谱中读取拐点值精度要更高。但是, 在不同量级条件下, 拐点也会呈现出以下几个特征。
1) 冲击量级的大小会影响样品响应的拐点个数, 一般来说量级越大, 样品被激励出的拐点越多、 越全面。
2) 样品上不同位置处的监测点, 样品被激励出的拐点个数和频率一般也不相同。
3) 对于样品上的比对点, 最好选择在不同的冲击量级下始终存在的第一个拐点, 或者某一个拐点, 这样有助于提高不同实验室间冲响比对的精度。
