跳车作用下新型波形钢腹板组合梁桥的动力响应分析

2022-09-01于海峰胡世浩

兰州交通大学学报 2022年4期

于海峰，胡世浩

（1.兰州交通大学土木工程学院，兰州 730070；2.上海市城市建设设计研究总院（集团）有限公司，上海 200125）

基于传统的钢-混组合梁桥，Nie等［1］提出了将带肋钢底板代替传统混凝土底板的新型波形钢腹板组合结构，由此出现了一种新型波形钢腹板组合梁桥，如图1所示.这种新型组合桥梁可以有效减轻桥梁自重，充分发挥材料潜能，提高预应力施加效率.近年来，在国内外桥梁建设与应用研究中得到了广泛关注［2-4］.

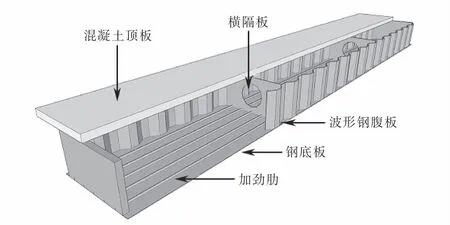
图1 新型波形钢腹板组合梁桥示意图Fig.1 Diagram of the new-type box girder bridges with corrugated steel webs

现实中车辆行驶通过桥梁时，桥面可能存在障碍物，车辆通过障碍物会产生跳跃冲击现象.车辆跳车不仅会引起桥梁结构和车辆的损害，严重的还可能会影响车辆的行驶安全，从而导致交通事故［5-6］.随着现代交通事业的飞速发展，近年来公路桥梁车辆跳车问题受到了众多学者的关注.大多数学者针对车辆跳车的研究主要集中于原因探究和防治措施等定性分析方面［7-8］，也有学者通过试验手段或解析方法研究车辆跳车问题.潘晓东等［9］通过大量的调查统计和行车试验研究了车辆跳车对驾驶舒适性的影响；张丽芳等［10］建立了5参数的车辆模型，分析了桥面沉降、车辆行驶速度等参数对简支梁桥动力响应特性的影响，但该5参数车辆模型与实际情况下的车辆结构相差较远；刘习军等［11］通过连续的小波分析方法，研究了各种道路工况下发生车辆跳车时对桥梁结构的冲击效应，较为准确地得到了桥梁不同部位发生车辆跳车时的动力响应.但是由于试验手段进行成本较高，因此有必要通过数值模拟的方法，采用更加合理的车辆模型和桥梁模型来深入研究跳车作用下的车桥耦合振动响应.

为科学定量地研究车辆跳车作用下新型波形钢腹板组合梁桥的动力响应特性，以一座跨径为30 m的新型波形钢腹板组合梁桥为研究对象，通过Universal Mechanism（UM）和ANSYS软件进行联合数值仿真研究了不考虑车辆跳车和考虑车辆跳车两种工况下桥梁的动力响应，计算了多因素影响下桥梁在移动车辆荷载作用下的动力冲击系数，并将结果与规范［12］中定义的动力冲击系数设计值进行了比较.

1 车桥耦合振动仿真模型

1.1 车辆模型的建立

选用与实际情况更相符的车辆模型对于准确获取梁桥动力响应至关重要.本文采用了更加符合实际情况的三轴车辆模型，该车辆模型的合理性在相关研究中已得到验证［13-14］.该车辆的相关参数取值如表1所列.如图2所示，MC，JC和IC分别代表车体质量、俯仰惯量和侧倾惯量；Csi（i=1，2，…，6）和Ksi（i=1，2，…，6）表示车辆悬架阻尼和车辆悬架刚度；Mti（i=1，2，…，10）为轮胎质量；αC和βC分别为俯仰角位移和侧倾角位移；Zti（i=1，2，…，10）为轮胎位移；L1，L2和L3分别表示车体质心至前、中和后轴的距离；ZC表示车体的浮沉位移；b1表示悬架中心至车辆质心轴的距离；b2表示较近一侧轮胎至车辆质心轴的距离；b3表示较远一侧轮胎至车辆质心轴的距离.车辆模型通过质量、弹簧和阻尼器模拟车辆的车体、悬挂和轮胎.轮胎采用基于弹性地基梁理论的Fiala轮胎模型，车轮与桥面采用车轮圆盘模型，比单点接触模型精度更高，能够准确反应车辆在实际行驶过程中的动态特性，如图3所示.

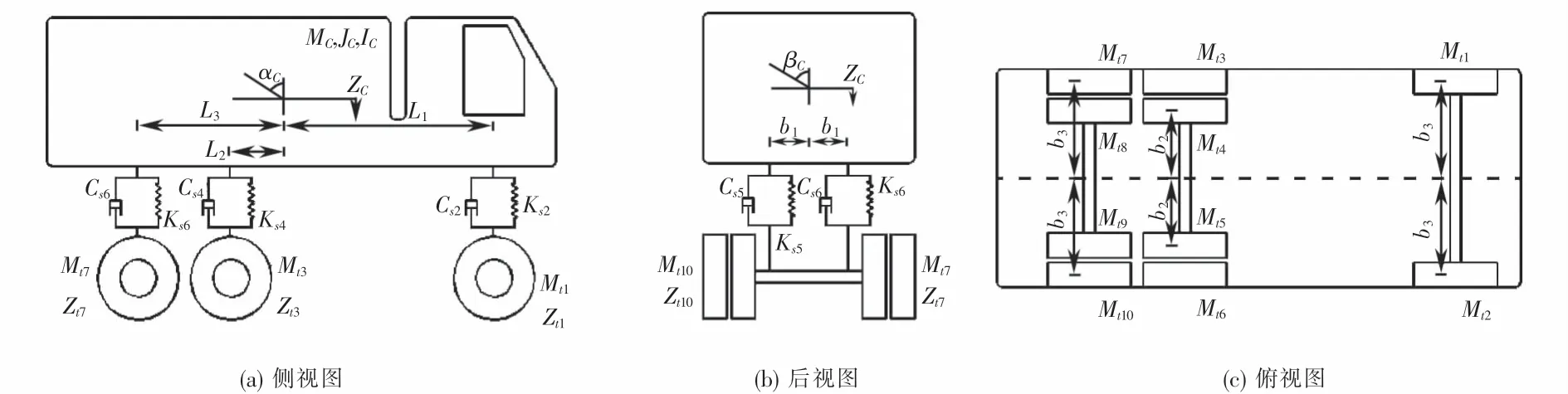
图2 车辆模型示意图Fig.2 Vehicle model diagram

图3 车辆三维仿真模型Fig.3 Simulation model of the vehicle

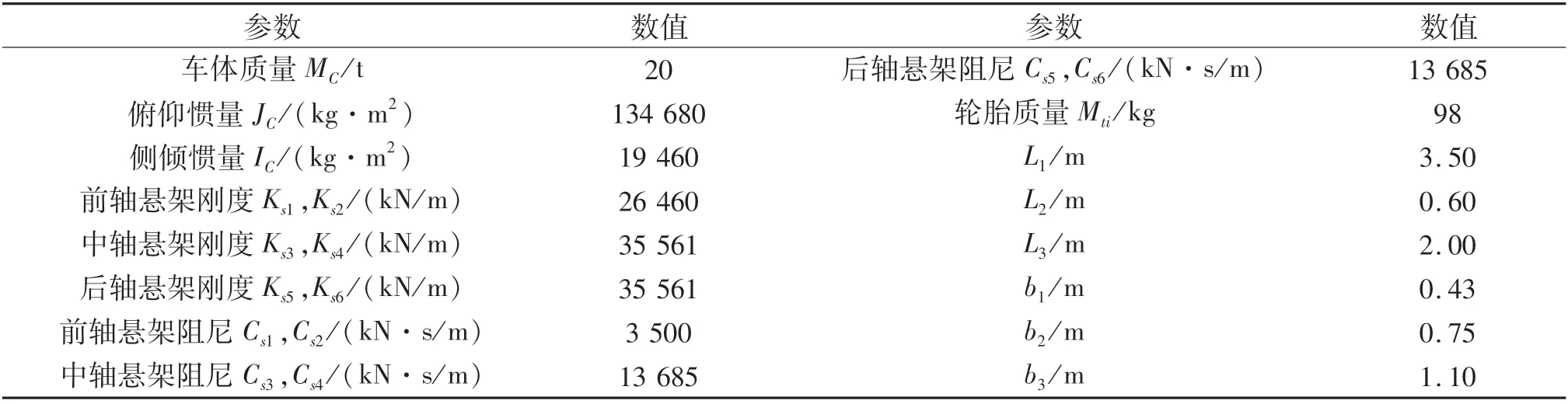
表1 车辆模型参数取值Tab.1 Vehicle model parameter value

可由达朗贝尔原理导出车辆的运动方程，表示为

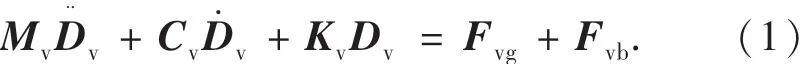
其中：Mv为车辆的质量矩阵；Cv为车辆的阻尼矩阵；Kv为车辆的刚度矩阵；Dv为车辆的位移矢量；Fvg为由车辆自重引起的荷载矢量；Fvb为轮胎变形引起的车桥相互作用力矢量.

1.2 路面不平整度模拟

1.3 跳车障碍物几何模型

车辆跳车现象通常由桥面障碍物引起，根据规范［16］中的障碍物信息，构建了跳车障碍物的几何模型.如图5所示，h为桥面跳车段高度，l为桥面跳车段长度.路面不平整度提供正常段的位移激励，桥面障碍物提供跳车段的位移激励［17］.在整个跳车过程中，假设障碍物为刚体，同时障碍物不发生任何平动、转动以及压缩变形.模拟过程中将障碍物布置在桥梁跨中部位，跳车段最高点距离桥面约为5～7 cm，跳车段水平长度为30 cm，跳车时车速一般为5～20 km/h.

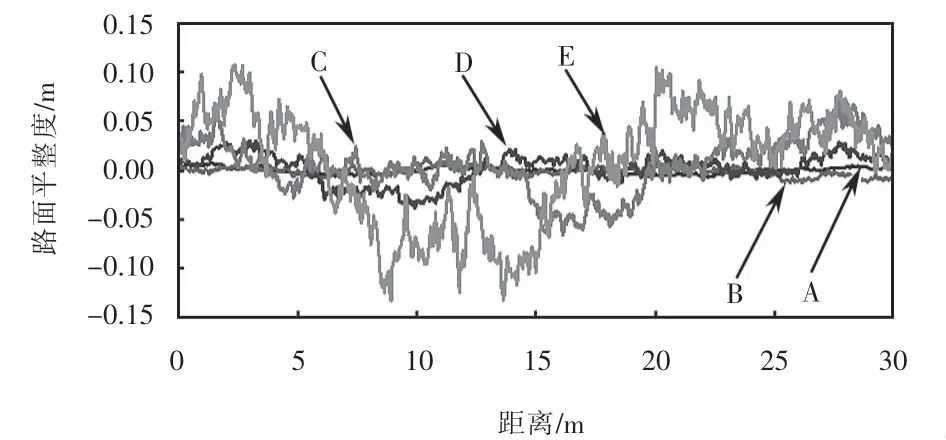
图4 路面不平整度样本曲线Fig.4 Spline curves of road roughness

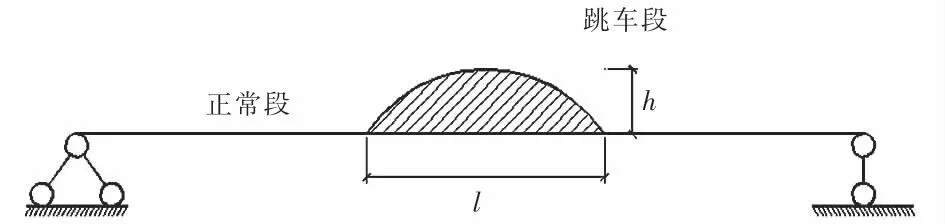
图5 车辆跳车示意图Fig.5 Diagram of vehicle jumping

1.4 桥梁模型的建立

甘肃省兰州新区南立交机场连接线公路工程项目是新型波形钢腹板组合梁桥在我国的第一次实际应用.本文的研究对象为其中一座宽20 m（4片主梁）的简支梁桥，桥梁长为30 m，高为1.5 m，其横截面尺寸如图6所示.波形钢腹板采用的是BCSW1200型号，具体尺寸如图7所示.结构材料方面，混凝土材料为C50，钢材采用Q345C.混凝土和钢材弹性模量分别是3.45×104Mpa和2.06×105Mpa；泊松比分别取0.2和0.3.

图6 桥梁横截面图（单位：mm）Fig.6 Bridge cross-section diagram（unit：mm）

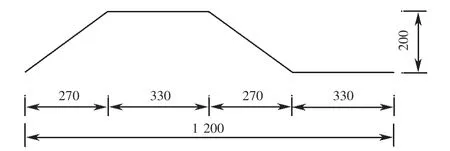
图7 波形钢腹板尺寸图（单位：mm）Fig.7 Geometry of corrugated steel web（unit：mm）

通过ANSYS软件构建桥梁的有限元模型如图8（a）所示.其中，混凝土和钢材分别采用SOLID45单元和SHELL63单元进行模拟.两种单元连接节点处通过节点耦合约束的方式建立刚性区域.全桥共建立节点52 575个，单元42 514个.通过ANSYS计算得到桥梁的第一阶竖向弯曲自振频率为3.791 Hz，一阶振型如图8（b）所示.

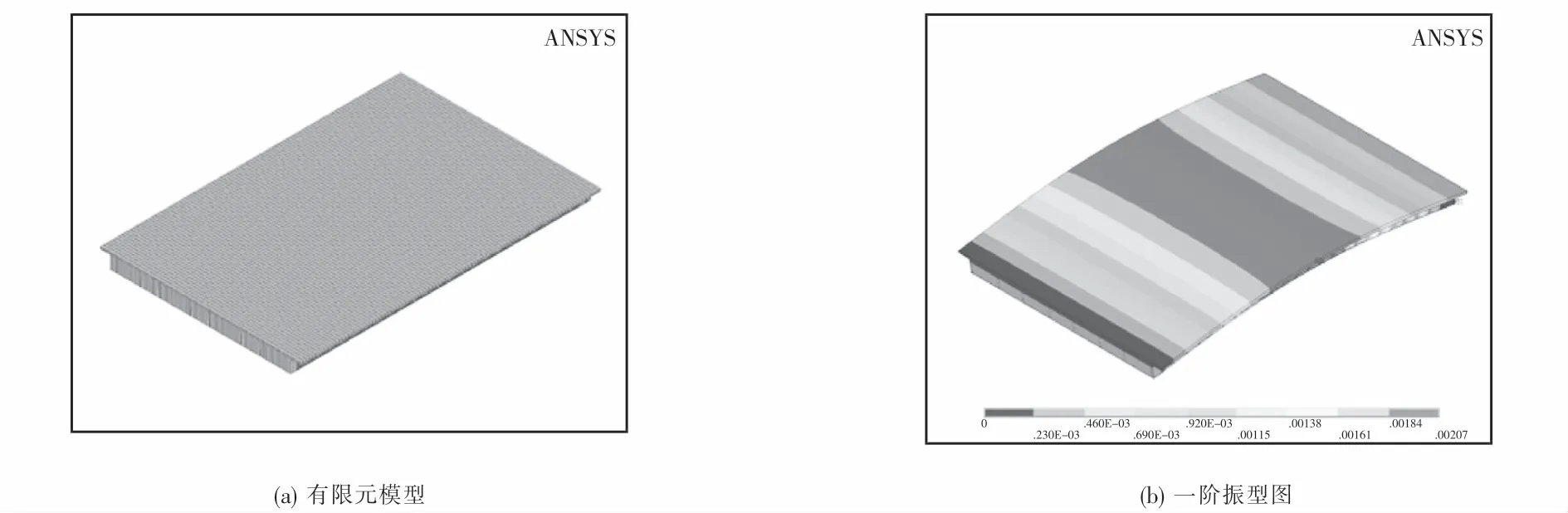
图8 有限元模型及振型图Fig.8 FE model and first-order mode shape of the composite girder

通过脉动法动力特性试验获取桥梁实测自振特性，得到前三阶竖向弯曲自振频率.桥梁现场试验状况如图9所示，功率谱密度如图10所示.

图9 现场数据采集图Fig.9 Data acquisition system

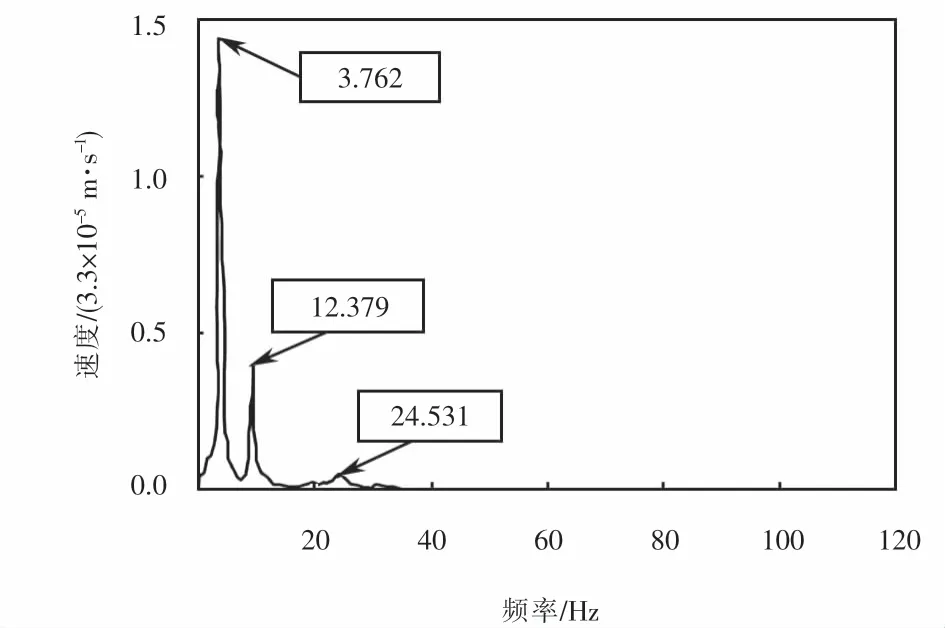
图10 功率谱密度图Fig.10 Power spectral density

通过对比桥梁自振频率实测值与ANSYS计算值，验证所建有限元模型的准确性，结果如表2所列.对比结果，两者一阶弯曲自振频率的误差仅为0.76%，数据吻合良好，表明有限元模型具有较高的准确性.

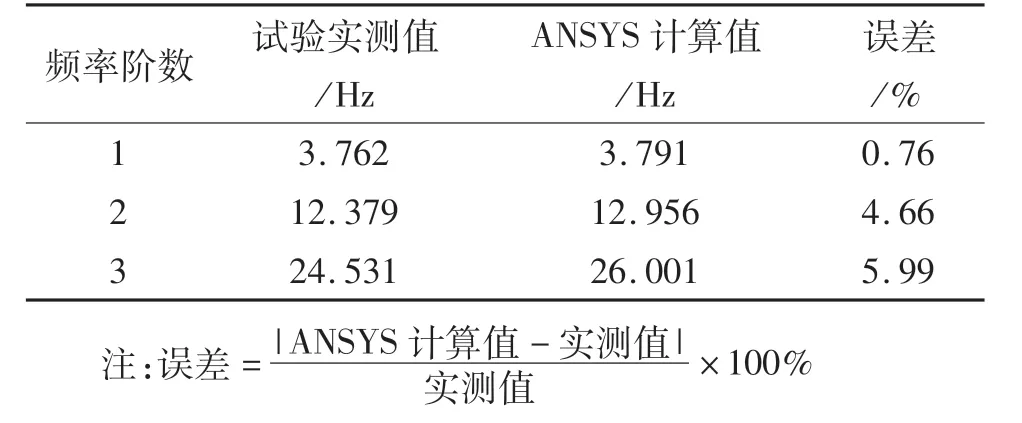
表2 竖向弯曲自振频率实测值与ANSYS计算值对比Tab.2 Comparison of the measured value and ANSYSvalue

1.5 车桥耦合模型的建立与验证

基于UM-ANSYS.exe接口程序将上文所建立的车辆模型和桥梁模型导入同一个UM仿真模型中，在UM软件中设置桥梁的约束节点，将车辆模型与桥梁模型进行耦合，得到车桥耦合振动仿真模型，如图11所示.为验证所建车桥耦合仿真模型的适用性，在ANSYS中也采用相同车辆荷载进行多荷载步静力加载，获得桥梁静挠度计算值，通过对比UM计算值，结果表明数据吻合良好，如图12所示，最大误差为1.48%，验证了所建车桥耦合仿真模型的适用性.

图11 车桥耦合模型示意图Fig.11 Diagram of the vehicle-bridge coupled model

图12 UM 和ANSYS静挠度计算值Fig.12 Comparing of the static deflection of UM and ANSYS

根据车桥接触点的位移协调关系和相互作用力关系［18］，车辆桥梁刚柔耦合模型的振动方程可表示为

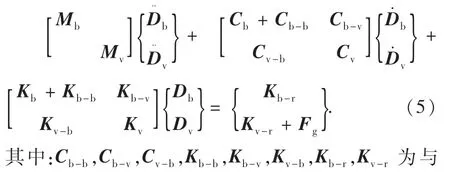
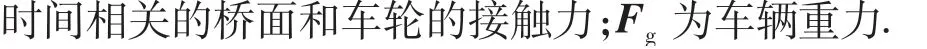
上文所建立的车桥耦合动力学方程在时域和频域内均可进行求解，采用较多的是时域计算方法中的直接积分法和综合模态法.通过直接积分法求解可能会耗费大量资源，甚至无法求解.因此，有学者提出综合模态法，这种新的求解方法在计算中忽略桥梁的高阶模态贡献，仅选取少量低阶模态参与计算，可大幅降低求解动力学方程的复杂程度［19］.本文基于ANSYS有限元软件建立高精度桥梁模型，采用固定界面模态综合法求解，剔除6个刚体模态.将高精度桥梁模型和车辆模型导入UM软件中形成车桥耦合系统，UM软件通过Park积分法求解车桥耦合振动方程.

在UM软件Simulation后处理程序中计算不同工况下车桥耦合振动的动力响应.具体仿真流程如图13所示.

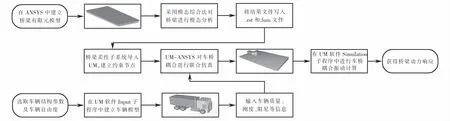
图13 车桥耦合振动仿真流程Fig.13 Simulation process of vehicle-bridge coupled system

2 数值分析

车辆行驶车道选取为2号主梁所对应车道，对于简支梁桥，桥梁的最大挠度响应和最大应变响应均出现在跨中截面.因此，选取桥梁跨中截面静响应最大的主梁底部作为具体控制点.计算工况如表3所列.

表3 车桥耦合仿真工况设置Tab.3 Working condition of vehicle-bridge coupled simulation

2.1 未发生跳车时桥梁动力响应

2.1.1 桥梁跨中挠度

为了研究路面不平整度对桥梁跨中挠度的影响规律，研究车辆以60 km/h的速度匀速通过桥梁，获取桥梁跨中截面控制点的挠度时程曲线，如图14所示.

从图14可以看出：路面不平整度对新型波形钢腹板组合梁桥跨中挠度影响较大.随着桥面平整状况的不断劣化，桥梁最大挠度波动幅度越来越大，在路面不平整度等级为好的情况下，挠度时程曲线基本呈抛物线趋势，当路面不平整度等级为差的情况时，挠度时程曲线则出现了很大的波动，抛物线已经不再显现.在路面不平整度等级为差的情况下，桥梁最大动挠度为3.739 mm，较路面不平整度等级为好时增加了32.7%.

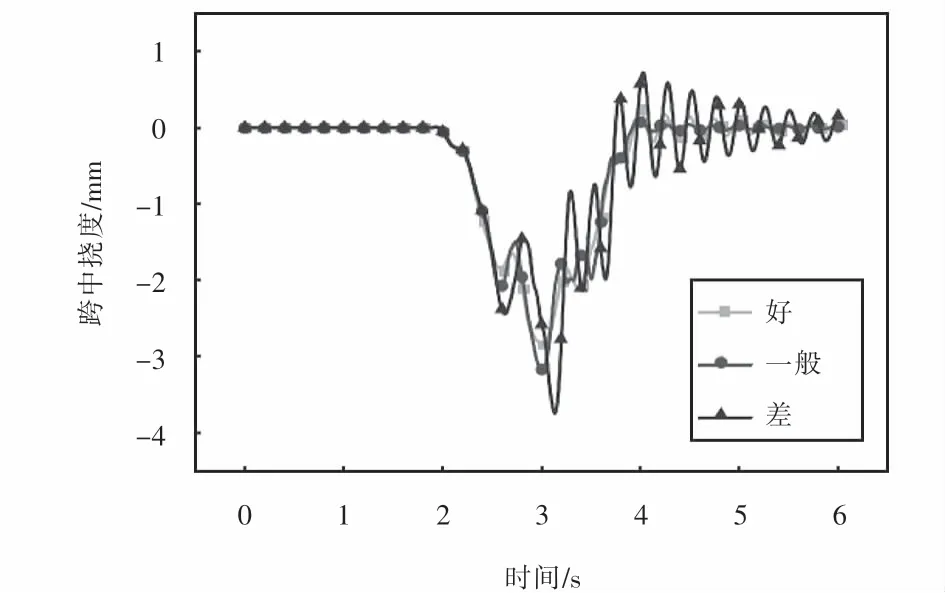
图14 不同路面等级下的挠度时程曲线Fig.14 Deflection curves under different road roughness

2.1.2 动力冲击系数

为了研究车辆行驶速度对动力冲击系数的影响规律，考虑在其他条件相同时，路面不平整度等级为好、一般、差三个等级，车辆以30～120 km/h、间距为15 km/h的速度匀速通过桥梁，研究其引起的动力冲击系数的变化规律，如图15所示.

从图15可以看出：在三种路面不平整度等级下，动力冲击系数随着车速的增加未表现出明显的单调变化趋势，而是整体出现先减小，后增大，再减小的变化趋势.对比发现，当路面不平整度等级为好时，动力冲击系数的计算值小于规范设计值；当路面不平整度等级为一般时，两者数据吻合良好；当路面不平整度等级为差时，动力冲击系数的计算值与规范设计值存在较大差异.因此，规范可能低估了路面状况较差时移动车辆引起的动力冲击效应.

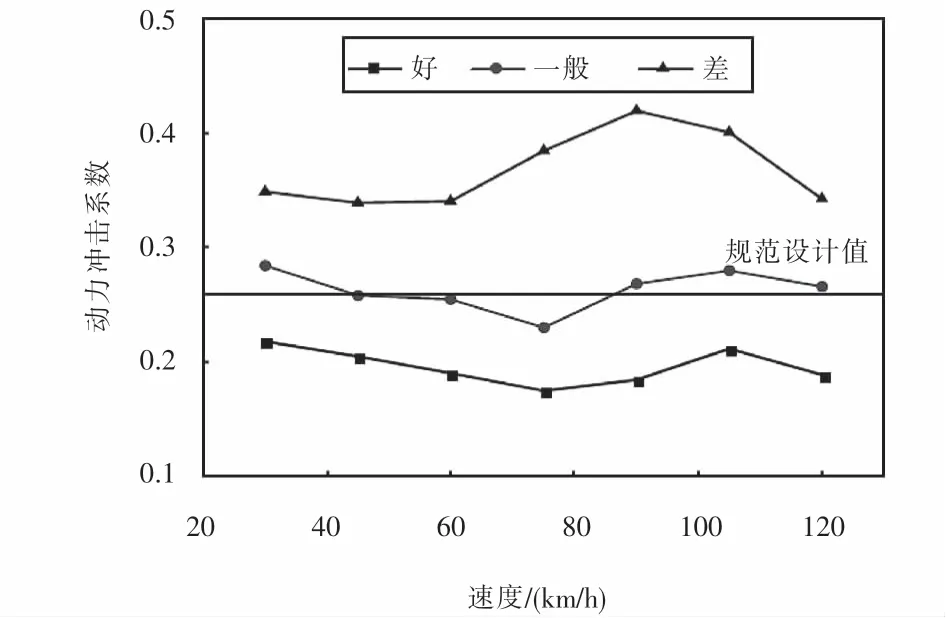
图15 不同车速影响下的动力冲击系数Fig.15 Impact factors under different vehicle speed conditions

2.2 发生跳车时桥梁动力响应

2.2.1 桥梁跨中挠度

车辆跳车可能会引起桥梁更明显的动力响应［20-21］.为了研究不同跳车速度、不同跳车高度对组合梁桥跨中挠度的影响规律，考虑路面不平整度等级为好，车辆以速度为5、10、15、20 km/h匀速通过桥面，车辆起跳高度为5、6、7 cm.以5 km/h为例，得到考虑车辆跳车作用下跨中截面控制点的挠度时程曲线，如图16所示.

将跳车行驶速度为5、10、15、20 km/h四种工况下的跳车冲击计算结果汇总，如表4所列.

从图16可以看出：在同一路面等级下，车辆在通过桥梁时，车辆跳车冲击效应对桥梁跨中挠度的影响显著.当未发生跳车时桥梁跨中挠度为2.573 mm，跳车5 cm时桥梁跨中挠度为3.607 mm，跳车6 cm时桥梁跨中挠度为3.903 mm，跳车7 cm时桥梁跨中挠度为4.546 mm.

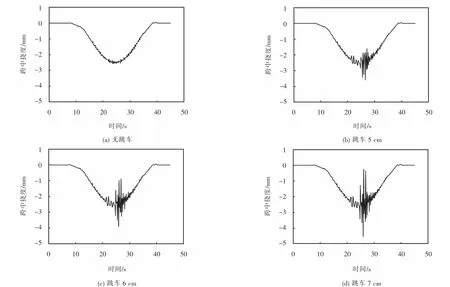
图16 考虑桥面跳车时的挠度时程曲线Fig.16 Deflection curves considering vehicle jumping

从表4可以看出：车辆以不同行驶速度通过桥梁会引起不同的动力响应，发生跳车冲击后，不同车速对桥梁跨中挠度影响不大.以跳车5 cm为例，车速5 km/h引起的桥梁跨中挠度最小，车速20 km/h引起的桥梁跨中挠度最大，两者差值仅为0.331 mm.

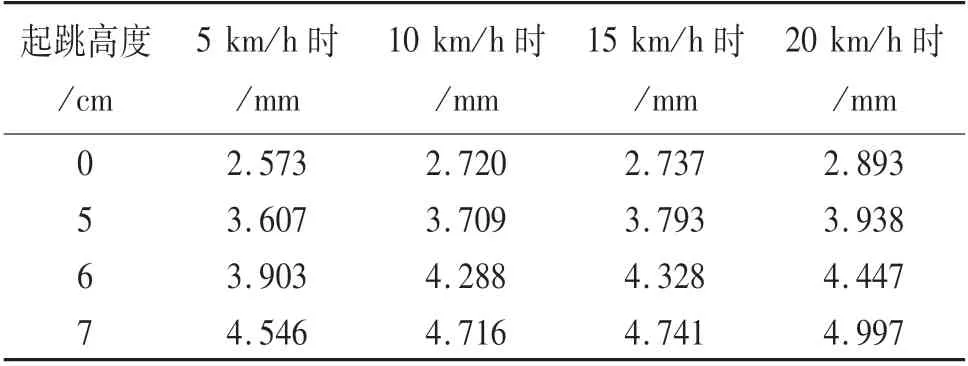
表4 车辆以不同速度发生跳车时桥梁跨中挠度Tab.4 Bridge mid-span deflection at different vehicle jumping speeds

2.2.2 动力冲击系数

为了研究不同跳车速度、不同跳车高度对组合梁桥动力冲击系数的影响，假设路面不平整度等级为好，起跳高度为5～7 cm，间距为1 cm，车辆以5～20 km/h，间距为5 km/h的速度通过桥梁，研究其引起的动力冲击系数变化规律，如图17所示.

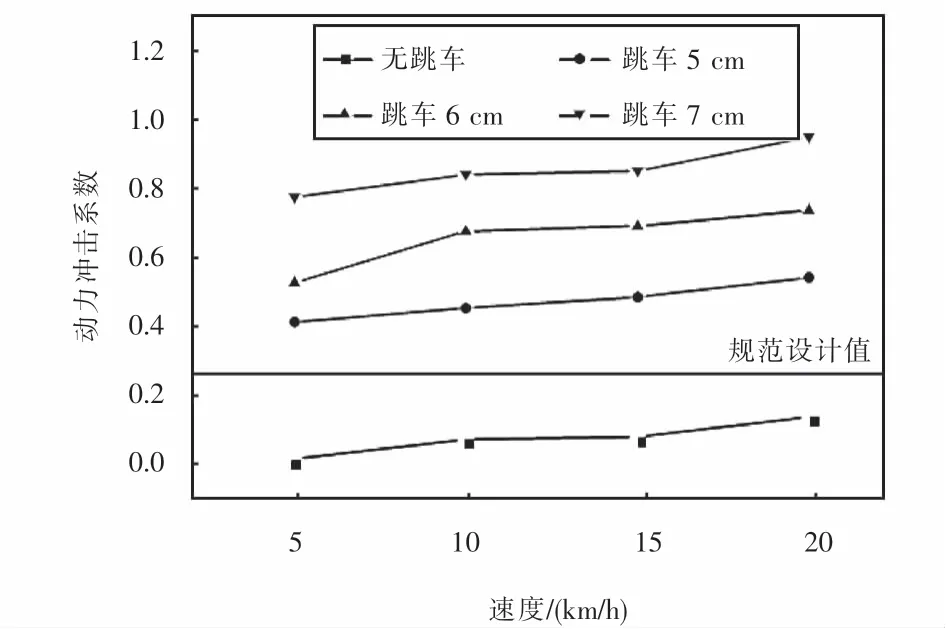
图17 跳车影响下的动力冲击系数Fig.17 Impact factors considering vehicle jumping

从图17可以看出：车辆跳车对动力冲击系数影响显著，以20 km/h为例，当未发生跳车时最大动力冲击系数为0.124，跳车5 cm时最大动力冲击系数为0.531，跳车6 cm时最大冲击系数为0.728，跳车7 cm时最大冲击系数可达0.942.比较可知：当发生跳车冲击时所引起的动力冲击系数均大于规范设计值.因此，该规范可能低估了车辆跳车现象对冲击效应的影响.当发生车辆跳车时，动力冲击系数与车速整体呈正相关趋势，在车速为20 km/h时动力冲击系数达到最大值.但相较而言，跳车高度对动力冲击系数的影响更大.