基于高斯混合模型的卫星电源系统异常检测方法
2022-09-01魏居辉王炯琦穆京京何章鸣周萱影
魏居辉, 王炯琦*, 穆京京, 何章鸣,3, 周萱影
1. 国防科技大学, 长沙 410073 2. 中国航天科技集团有限公司, 北京 100090 3. 北京空间飞行器总体设计部, 北京 100090
0 引 言
卫星电源系统作为卫星的重要组成部分,承担着为星上负载或产品供电的功能.卫星在轨运行期间,复杂的太空环境会导致卫星电源系统异常,使得卫星供电系统中断,影响卫星的平稳运行,或导致卫星的失效.开展卫星电源系统的异常检测研究,能够有效监测卫星电源系统状态,实现系统异常的预警,从而提升卫星在轨运行可靠性.近年来,针对卫星电源系统的异常检测研究已引起国内外研究学者的关注,主要有两种[1-2]:基于解析模型的方法和基于数据驱动的方法.1)基于解析模型的异常检测方法.系统具备一个较准确的数学模型,可以将量测信息和参考输出进行比较得到残差,通过对残差进行分析处理从而实现异常检测[3].具体包括参数估计方法、状态估计方法和等价空间方法等[4].2)基于数据驱动的异常检测方法.系统不具备一个精确的数学模型,只能对研究对象的结构特性以及各类型故障发生时各传感器数据进行分析处理从而实现异常检测[5].具体包括信号处理方法、信息融合方法、机器学习方法、多元统计分析方法以及专家知识方法等[6].
为满足不同的任务需求,卫星电源系统会在不同的工作模式之间进行切换,使得建立精确模型变得困难.从而导致了系统可测信息和参考模型输出偏差较大,使得基于解析模型的异常检测方法应用受限[7].相反,对卫星电源系统实施观测相对更容易,根据目前已经掌握大量历史数据的现况,基于数据驱动的卫星电源系统异常检测方法更具有发展前景[8].因此,大量的学者就数据驱动的异常检测方法开展了深入的研究,主要工作如下:
文献[9]最先提出基于距离的异常检测方法,将异常点定义为没有足够多相邻数据点的数据点,利用数据分布不一致性对异常点进行检测.但在高维空间中,基于欧式距离的度量变得不稳定,使得异常检测效果降低.文献[10-11]进一步提出了基于角度的异常检测方法,利用角度在高维数据中的稳定表现来提升异常检测的稳定性.但是,该方法需要计算全局的信息,计算负荷较大.为了减少计算负荷,文献[12-13]提出了基于局部密度的异常检测方法,利用局部向量点积密度来度量各数据点的异常程度,并利用最大斜率模型确定异常检测阈值,该方法确实显著降低了计算负荷.进一步,文献[14-15]提出了基于概率的异常检测方法,利用贝叶斯后验概率构建了一种异常检测算法,用于识别一类更新速度快、变化趋势平缓、缺少人工类别标识的时间序列异常值.但是,该方法需要预先假定数据符合某个概率模型,然后才能根据此分布模型对待检测数据进行不一致性检测来判别异常值.
对于具有多种工作模式的卫星电源系统,实际观测数据(或数据统计特征)难以用预设的概率模型进行刻画,且无法事先知道数据中的异常值个数,因此,上述方法具有一定的局限性.当数据缺少标记时,由于无法获取异常标记,该方法会失效.文献[16-19]提出了一种基于高斯混合模型(GMM)的异常检测算法,利用高斯混合模型对历史数据进行聚类分析,获取不同模式的聚类中心,并生成统计模型.该方法应用于工业领域取得了理想的效果.目前,针对状态标识缺失的多模式卫星电源系统开展的异常检测研究仍然较少.其研究主要存在下述两个难点:1)如何实现无标识的数据建模;2)如何辨识建模过程中的参数.
由于卫星电源系统是典型的多模式系统,因此基于高斯混合模型的异常检测方法可以适用于卫星电源系统的异常检测.本文在基于高斯混合模型的卫星电源系统异常检测方法上,构建了可区分性、稳定性和拟合优良性3个准则对模型的拟合效果进行评价,解决了高斯混合模型易受到聚类簇数和初始迭代点影响的问题.同时,本文将该方法用于卫星电源系统异常检测中,在缺少系统模型和模式标识的情况下,取得较好的检测结果,验证了该方法在卫星系统中的应用可行性.
1 高斯混合模型
卫星电源系统中的大多数设备都存在多种不同的工作模式(或工作环境),记这些不同的工作模式为D={D1,D2,…,Ds}.对于在指定模式Di,i=1,2,…,s下稳定工作的设备,其观测数据本身(或观测数据的特征)通常表现出平稳的特性.因此,通常假设模式Di下的观测数据xij满足如下的观测方程
xij=ηi+Aiε,j=1,2,…,mi
(1)
式中,xij∈Rn×1是n维的系统观测数据,ηi∈Rn×1表示数据均值,Ai∈Rn×n是误差生成矩阵,ε∈Rn×1表示观测过程中不可观不可控因素引起的随机误差.通常认为ε服从均值为0,方差为In的标准正态分布
ε~N(0,In)
(2)


(3)
由于系统会在多种工作模式之间进行切换,因此在事先不确定系统运行模式时,通常认为观测数据以一定的概率来自某个模式.为了后续表述方便,做如下记号:

(4)
式中,η表示所有模式均值的集合,Σ表示所有模式方差的集合.此时,多模式下的观测数据xij满足如下的高斯混合模型(Gaussian mixture models, GMM)

(5)


(6)
由于卫星电源系统的实际观测数据往往无法提供状态模式标识作为先验信息,而模型中包含与模式标识相关的隐变量αi,无法通过直接求解获得GMM的最大似然解,因此,需要使用迭代的方法对模型进行求解.
2 EM算法及模型评估
2.1 EM算法
为了通过训练数据获得高斯混合模型的极大似然解,需要使用迭代的方法.期望最大化算法(EM)是求解该模型的典型算法,同时,文献[20]表明该算法可以收敛到一个稳定解,其具体迭代步骤如下.
步骤1.初始化,给定精度ε选定初始迭代参数
步骤2.E步骤,使用t(t=0,1,…,tmax)次迭代的参数值计算


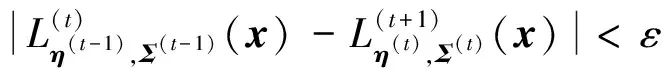
2.2 模型评估
利用EM算法可以对GMM模型进行求解.由于模型的聚类结果易受聚类簇数和初始参数的影响,因此,需要对GMM的建模精度进行评估,以确保模型不出现欠拟合和过拟合的问题.进一步,本文考虑了以下几种评价准则.
2.2.1 可区分性准则
首先,设备在不同模式下的观测数据应当具有显著差异,这是显而易见的一点.实际上,这暗示着每个模式有明确可区分的聚类中心,换言之,每种模式的聚类中心不应当位于其他模式的置信区间内.因此,准则1给出了GMM模型可区分性的定义,而一个好的GMM模型总是可区分的.
准则1.(可区分性) 称两个模式Di,Dj是可区分的,如果其满足下述条件
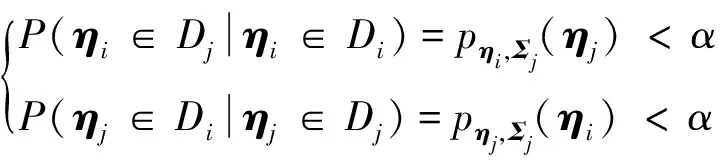
(7)
式中,ηi,ηj分别是模式Di,Dj的观测数据的聚类中心1-α是置信水平,一般为0.05.进一步,称一个GMM模型的任意两个模式Di,Dj都是可区分则称该模型是可区分的.在准则1的条件下,图1直观地展现两个模式是否是可区分的.

图1 模式可区分性示意图Fig.1 Model distinguishability diagram
图1中,模式1和模式2的聚类中心并不落在彼此的置信区间内,因此模式1和模式2是可区分的;然而,模式2和模式3的聚类中心落在了彼此的置信区间内,因此模式2和模式3是不可区分的.综合上述,选择模式数量为3时,该模型是一个不可区分的模型.
2.2.2 稳定性准则
其次,在选取合适的模式簇数后,GMM模型应当是稳定的.这也就是说,对于不同的初始参数,最终的模型聚类结果应当不存在显著差异.因此,准则2给出了GMM模型稳定性的定义,而一个好的GMM模型总是稳定的.
准则2.(稳定性)称一个模型是稳定的,如果其对任意的初始参数{η(0),Σ(0),α(0)},迭代后获得的{η*,Σ*,α*}是无显著差异的,则称该模型是稳定的.由于,针对任意初始参数来验证模型稳定性是一件困难的事情,因此,通常仅利用2组不同的初始参数进行验证.在准则2的条件下,图2直观地展现GMM模型是否是稳定的.

图2 模式稳定性示意图Fig.2 Telemetry Data Chart
在图2中,仍然采用图1中的数据,模式簇数仍然选择为3,但是选用了不同的初始迭代点.可见模式2的聚类中心发生了改变,因此,该模型是不稳定的.
2.2.3 AIC准则和BIC准则
上述两个准则从定性的角度对GMM模型的好坏进行了评价.为了定量地评估GMM模型的聚类精度,下文考虑了AIC准则和BIC准则.这两个准则是常用的衡量统计模型拟合优良性的准则.
为了检验GMM模型的拟合优良性,总是考察模型的似然函数值和未知参数个数.通常,似然函数值越大说明模型拟合的效果越好;未知参数个数越多,说明模型越灵活,拟合准确度就会越高.尽管增加模型参数个数会提高模型拟合准确度,但是,这会增加模型过拟合的风险.因此,一个好的拟合模型应该是一个拟合精度和未知参数个数的综合最优配置.AIC准则和BIC准则都是基于这一思想提出的.
AIC准则(akaike information criterion)[21]:对于GMM模型而言,可以用拟合精度和参数个数的加权函数来表征模型的拟合优良性,公式如下:
AIC=s-Lη,Σ(x)
(8)
式中,s代表GMM模型的参数数量,Lη,Σ(x)代表GMM模型的对数似然函数,AIC函数值越小表明模型拟合效果越好.
BIC准则(bayesian information criterion)[22]:对于GMM模型而言,可以用拟合精度和参数个数的加权函数来表征模型的拟合优良性,公式如下:
BIC=slnm-2Lη,Σ(x)
(9)
式中,s代表GMM模型的参数数量,m为样本容量,Lη,Σ(x)代表GMM模型的对数似然函数,BIC函数值越小表明模型拟合效果越好.
相比较于AIC准则,BIC准则将未知参数个数的惩罚权重由常数变成了样本容量的对数函数lnm.由于BIC准则考虑了样本容量,因此可以有效防止模型拟合准确度造成的模型复杂度过高的问题.
3 异常检测准则与精度评估
在第2节中,EM算法被用于高斯混合模型的求解,从而实现了通过历史数据对不同模式特征的聚类分析.接下来,就可以构建合适的异常检测准则来实现待检测数据的异常检测,最后,还应当对异常检测的精度进行分析与评估.
3.1 模式判别
通常,相比较于使用单次观测数据进行异常检测,利用多次观测数据进行异常检测能取得更高的检测精度,因此,考虑待检测数据集Z={z1,z2,…,zk}.在基于距离的判别方法下,待检测数据Z所属模式Di由下式确定

(10)
式中,d2(Z,Di)表示待检测数据集Z到模式Di的距离.一般而言,马氏距离是一个合适的度量准则,其计算方法由下式确定

(11)

3.2 F检验方法
确定待检测数据集Z所属模式Di后,还需要检验Z是否确属于模式Di.通常可以构建如下统计量:

(12)
文献[23]表明,该统计量满足参数为n和mi+k-n-1的F分布,即
F~F(n,mi+k-n-1)
(13)
由于
mi=mp(Di)=mαi
(14)
从而可以写成如下形式:
F~F(n,mαi+k-n-1)
(15)
在置信水平α下,若统计量F满足
F (16) 则认为待检测数据集Z中数据都正常,否则认为待检测数据集Z中存在异常数据. 由于卫星电源系统通常是高可靠的,系统出现异常的情况总是相对少的,所以,利用多次观测数据进行异常检测通常能够减少工作量.但是,待检测数据集Z中存在异常数据时,仍然需对数据集Z进行更细致的分析来定位异常.因此,下述流程被用于异常数据的精确定位. 如果待检测数据集Z中存在异常数据,则构建删减数据集Zi如下: Zi=Z-{zi}={z1,z2,…,zi-1,zi+1,…,zk} 类似于公式(12),在删减数据集Zi上构建统计量 (17) 由于该统计量表征了删减数据集Zi与模式Di的偏离程度,所以,有理由认为异常数据zi是使得统计量Fzi最小的数据,即 (18) 同理,式(17)中的统计量Fzi满足参数为n和mαi+k-n-2的F分布,即 Fzi~F(n,mαi+k-n-2) (19) 在置信水平α下,若统计量Fzi满足 Fzi (20) 则认为删减数据集Zi中数据都是正常的,而zi确是一个异常数据;否则,删减数据集Zi中仍然存在异常数据,需要针对Zi继续构建删减数据集,并重复上述过程,直到确定所有的异常数据,整个流程如图3所示. 图3 异常检测流程图Fig.3 Abnormal detection flow chart 注1.式(14)中mi=mαi不一定是整数,因此需要考虑参数为n1和n2的F分布的概率密度函数 (21) 其中,B(·|·)表示贝塔函数,具有如下的形式 (22) 为了评估异常检测效果,采用精确度(Pre)、召回率(Rec)和F1分数三个指标对异常检测效果进行评估,如式(23)所示,各项指标越高,表示检测效果越好. (23) 式中:TN是被正确检出的正常样本个数;FP是被错误检出的异常样本个数;FN是被错误检出的正常样本个数;TP是被正确检出的异常样本个数,相互关系如表1所示. 表1 标签相互关系表Tab.1 The relationship between label 在实际应用中,数据标签是未知的,这导致实际的异常检测结果是不可预见的,也就是说无法在没有外界信息输入的情况下进行精度评估.因此,为了对方法效果进行评估,在已经标注的数据集上进行训练测试是必要的.值得注意的是,数据的标注并不作为先验信息来辅助模型的训练、测试以及异常检测,而仅在后续的精度评估中发挥作用. 卫星帆板驱动机构(SADA)是卫星电源系统的核心机构,如图4所示,在卫星的正常运行中发挥着重要的作用.由于卫星帆板系统直接暴露在太空中,容易受到空间碎片等侵袭,造成系统异常.因此,在卫星运行过程中,开展卫星帆板驱动机构的异常检测,能够对系统异常是一项很重要的任务.下面,以卫星帆板驱动机构为对象,开展了卫星电源系统异常检测的数值仿真和实验验证. 图4 SADA系统示意图Fig.4 Structure model of the SADA system 文献[24]给出了卫星帆板驱动机构的数学模型: (24) 式中,ISADA是太阳电池阵的输出电流,U是输出电压,θ为太阳光照射在太阳能帆板上时与太阳能帆板法线方向的夹角.Tb=25℃表示参考温度,Gb=1 000 W/m2表示参考光照强度,T表示实际温度,G表示实际光照强度.Vk,Vm,Id,Im为卫星太阳能帆板的固定参数,分别表示开路电压、最大功率点电压、短路电流、最大功率电流点.Nb是电池片并联数目,Nc是电池片串联数目.A,B,C表示补偿系数,分别为 A=0.002 5℃-1,B=0.000 5 m2/W, C=0.002 9℃-1 上述模型表明GEO卫星的太阳能帆板机构在不同工作模式(或工作环境)下通常具有稳定的输出.因此,在后续的建模过程中,无需进行额外的特征提取,同时,这表明高斯混合模型是适用的. 注2.实际情况中,卫星的工作环境不断变化,真实光照强度和真实温度都是不断变化的.在数值仿真中,为了简化模型,总是认为真实光照强度和真实温度都是固定值. 注3.GEO卫星的运行周期为24 h,全年中只有春分和秋分前后存在地影期,共92天,持续时间约为72 min,其余时间系统均运行于光照期.在数值仿真中,为了简化模型,不考虑光-地影过渡期. 注4.为了模拟实际环境中的温度变化、系统数据观测时的噪音干扰和数据传输过程中的传输损耗等影响,对测试参数的模拟量中加入±5%的高斯噪声. 文献[25]表明,卫星电源系统的故障以突变故障为主,主要包括: 1)电路异常,通常表现为部分太阳能板短路失效.在仿真过程中,可以等价为有效工作单元减少,即电池片并联数目Nb和串联数目Nc减少,本文假设并联数目Nc减少为0.95Nc. 2)定向机构异常,通常表现为太阳能帆板轴承机构卡死.在仿真过程中,可以等价为太阳光照射在太阳能帆板上时与太阳能帆板法线方向的夹角θ发生偏移,本文中假设存在θ产生10°的固定偏移. 因此,本文仅针对突变故障进行仿真.本文所有仿真在 Lenovo Ryzen 3700X CPU with 3.60 GHz processor, 16 GB RAM上进行.根据实际的情况,考虑卫星的两种运行环境,分别为光照期和地影期.两种环境下的参数设置如下 (25) 仿真时间设置为40 000 s,光照期和地影期的每次持续时间为5 000 s.前10 000 s系统正常运行,得到的数据作为训练集数据,随后的数据作为训练数据.在10 000 s时发生定向机构故障,在20 000 s时发生电路故障,30 000 s后,异常解除,卫星帆板驱动机构恢复正常运行.整个过程中,卫星帆板驱动机构的观测数据如图5所示. 图5 训练数据和测试数据图Fig.5 Training data and test data 首先,针对不同的聚类簇数,计算了不同聚类簇数下的AIC和BIC指标,结果如下图6所示.从图中可以发现,选择聚类簇数k=2时,AIC指标和BIC指标均取得极小值.同时,根据参数设置式(25)可知,卫星驱动机构主要存在两种工作模式,这验证了使用聚类簇数k=2是合理的.下图7给出了训练集数据的聚类结果,从图中可以发现,该方法能够较好地实现光照期数据和地影期数据的聚类. 图6 不同聚类簇数下的AIC指标和BIC指标变化趋势图Fig.6 Trend chart of AIC and BIC 图7 训练集数据聚类结果散点图Fig.7 Clustering results of training data (Take s=2 as an example) 在后续的异常检测中,以每10个数据作为1组测试数据集为例进行异常检测.此时,由式(16)可知,在置信度水平为95%的情况下,由F检验方法所确定的异常检测的阈值为 Threshold=Fα/2(n,mαi+k-n-1)=2.997 5 对训练集和测试集的检测结果如图8所示. 图8 异常检测结果图(以s=7,k=5为例)Fig.8 Abnormal detection results (take s=7,k=5 as examples) 从图8中可以发现,该方法可以识别发生在光照期的电路异常和驱动机构异常.这是由于,在光照期时,系统发生异常时会导致系统观测状态改变,从而可以对异常进行有效检测;而在地影期时,系统的异常无法对电流电压的观测值造成改变,从而导致无法对异常进行有效检测.事实上,为了检验地影期的异常数据,往往需要更多的观测信息,比如温度变化、蓄电池工作状态、轴承温度等.为了更直观地表现检测效果,将不同聚类簇数、不同待检测集长度下的检测效果汇总如表2. 表2 不同聚类簇数和不同待检测集长度下检测效果表Tab.2 Test results under different cluster number and length of different testing data 从表2中可以发现,在聚类簇数为s=2时,当待检测数据集长度增加时,各项指标都存在显著下降.这是由于卫星电源系统在地影期发生异常时,没有对电流和电压这两个指标产生影响,从而也就无法基于当前数据对卫星电源系统的异常做出检测.而随着待检测数据集长度的增加,该方法仍认为地影期数据没有与历史数据产生偏移,从而导致了对系统异常检测效果的下降. 上述数值仿真初步验证了基于高斯混合模型的异常检测方法在以卫星太阳能帆板机构为代表的卫星电源系统上的有效性.该方法在AIC指标和BIC指标极小的情况下,可以有效检出系统异常.因此,可以为后续的实际实验验证奠定基础. 本文的实验验证数据为某卫星电源系统的在轨遥测数据,由中国空间技术研究院提供.数据采样信息包括卫星太阳帆板的输出总电流、轴承温度和机构外壳温度等,采用PCA方法对所使用数据进行了降维,仅保留了3个主要特征. 训练集数据为2016年6月1日到2018年6月1日卫星太阳帆板机构的各信道遥测数据,测试集数据为2018年7月1日到2020年8月1日卫星太阳帆板机构的各信道遥测数据,在2020年7月7日到2020年7月13日期间,卫星太阳帆板发生执行器异常,观测数据如图9所示. 图9 某卫星电源系统训练数据图Fig.9 The training data and testing data (Actual observation data) 相比仿真数据,实际数据在空间中同样保持有两个明显的中心,但在不同模式之间存在状态转移过程,弱化了两个模式的界限.进一步,卫星的故障模式主要为定向机构故障,但比仿真数据中的故障形式更加复杂,从观测数据上来看,其分布也没有形成明显的聚类. 4.2.1 实验过程 首先,选取不同的聚类簇数,利用EM算法对模型进行求解,并计算了不同聚类簇数下的AIC函数值和BIC函数值,其结果如图10所示. 从图10中可以发现,当聚类簇数k>20时,AIC和BIC几乎没有发生改变.因此,在后续的研究中,仅考虑聚类簇数k=1,2,…,20的情况.进一步,考虑到GMM模型的可区分性,计算了不同聚类簇数下,聚类中心的可区分性,其结果如下图11所示(展示了k=7,8的情况).可以发现,当k>7时,GMM模型是不可区分性,因此,在后续的讨论中,仅考虑k=1,2,…,7的情况. 图10 不同数下的AIC和BIC函数值Fig.10 Trend chart of AIC and BIC 图11 不同聚类簇数下的模型可区分性(上图为k=7,下图为k=8)Fig.11 Distance between cluster centers under different cluster numbers 为此,以k=7为例,图12给出了聚类的效果. 图12 训练数据的聚类结果(以s=7为例)Fig.12 Cluster results of training data (Take s=7 as an example) 4.2.2 异常检测结果评估 在前文的基础上,分别选取聚类簇数s=1,2,…,7和待检测数据窗口长度k=1,5,10,30对异常检测结果进行评估. 表3表明如下的几点问题: 表3 不同聚类簇数和待检测集长度下检测效果表Tab.3 Test results under different cluster number and different length of testing data 1)Rec指标几乎没有改变.这是由于异常数据和正常数据存在较大的差异,容易被检测出来; 2) 在选择相同聚类簇数的情况下,随着测试数据窗口长度的增加,检测效果不断提升.这是由于数据窗口长度的增加带来了更多的信息,从而有助于提升异常检测效果. 3) 但是,在相同长度的测试数据窗口下,聚类簇数的增加并没有提升检测效果.这是由于,随着聚类簇数的增加,对训练数据的拟合精度增加,从而导致对检测数据的偏离敏感,使得正常数据也容易被误判为异常,导致检测效果降低.因此,在实际应用中,往往选取较小的聚类簇数来避免这个问题. 针对状态标识缺失的多模式卫星电源系统,本文提出了基于高斯混合模型的异常检测方法.首先,高斯混合模型被用于观测数据的建模;其次,EM算法被用于高斯混合模型的求解,可区分性准则、稳定性准则、AIC和BIC被用于模型的评估;随后,在高斯混合模型的基础上,模式判别准则和异常检测准则被用于卫星电源系统异常检测. 仿真和实验结果表明,高斯混合模型适合于卫星电源系统的建模,并且AIC和BIC的幅值变化过程表明了该方法的优良性.同时,在模式判别准则和异常检测准则下,Pre、Rec和F1等表明了该方法能够有效识别系统异常.最后,实验还表明,适当增加族类个数能够提高高斯混合模型的数据拟合精度并减小高斯参数的估计偏差,适当增加检测数据窗口长度能够提高异常数据识别精度,从而提高卫星电源系统的异常检测效果.
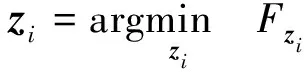



3.4 精度评估


4 数值仿真和实验验证

4.1 仿真数据验证


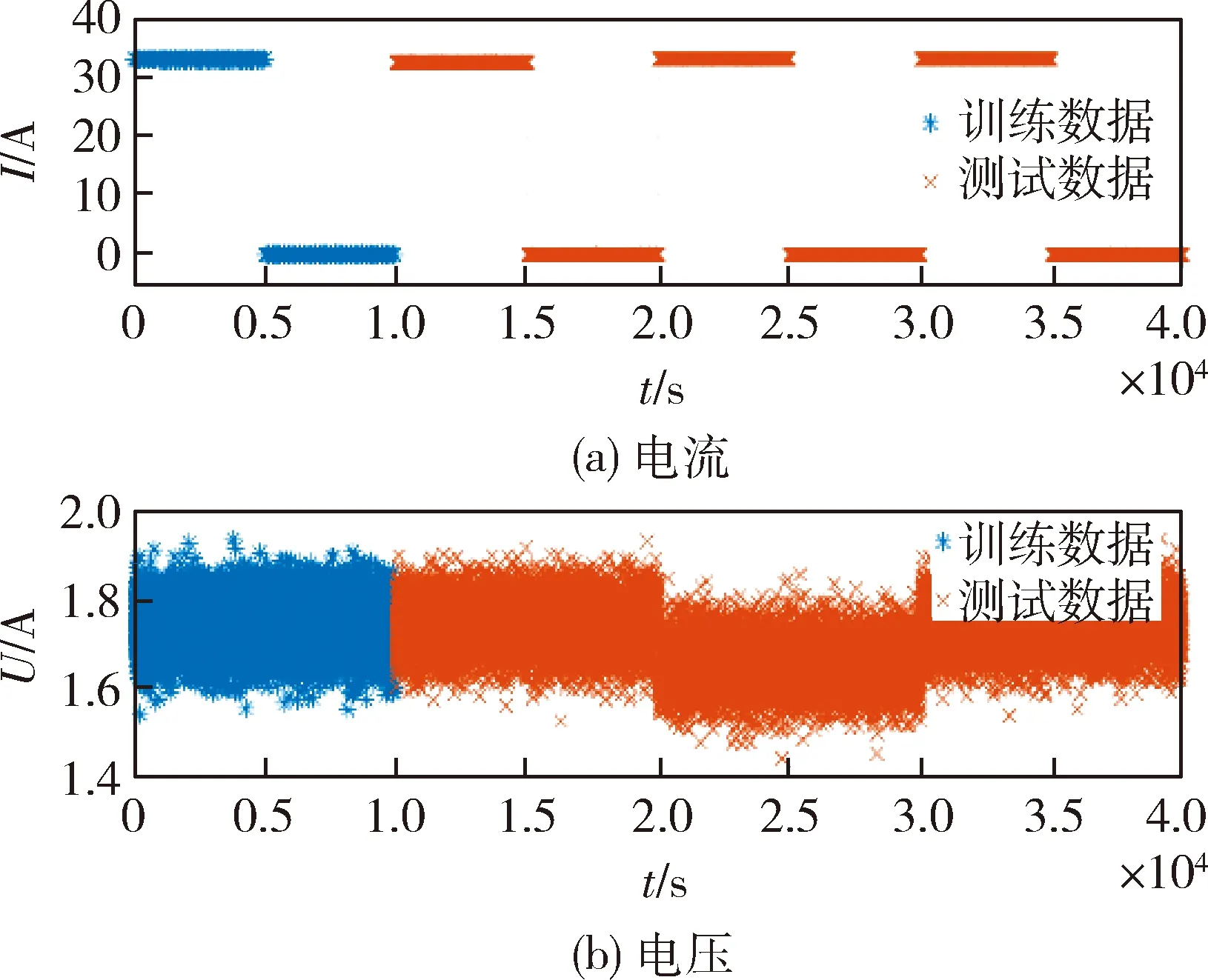



4.2 实际数据验证




5 结 论
