星载阵列天线型面优化调节方法研究
2022-09-01彭海阔张如变
陈 夜, 彭海阔, 李 奇, 张如变, 王 萌
上海卫星工程研究所,上海 201109
0 引 言
大尺寸星载天线是当前卫星技术领域的研究热点,大尺寸是提高天线信息容量,实现高分辨率的关键[1].轨道环境下,卫星的外热流变化剧烈,天线结构上的温度呈现大幅周期性变化[2-3],导致天线阵面的型面精度降低,影响天线的性能甚至引发载荷失效[4].
传统的天线变形控制方案是在天线结构上大量使用低变形复合材料,通过开展复合铺层的零膨胀设计,结构件的膨胀系数可达10-6/K以下[5-7].但随着天线尺寸的增大,材料的微小变形将发生累积,仅仅依靠材料的低膨胀设计已难以保证型面精度.为此,国内外相继开展了天线型面主动调节技术的研究.美国NASA研制的James Webb太空望远镜,通过镜面模块上的六脚作动器与曲率调节系统,在-220℃的低温环境下,主镜型面精度可保持在183 nm[8-9].俄罗斯Millimetron项目的红外望远镜,通过采用结构位形激光测量系统与型面作动调节系统,预计可将10 m口径的主镜型面精度控制在10 μm以内[10-11].
国内相关技术研究起步较晚,代表性的成果有数字近景摄影测量技术[12-14],文献[15]利用此技术对口径为5 m的星载固面天线开展了热变形测量试验,全阵面位置测量误差在40 μm以内,实现了大型阵面的高精度测量.在型面调节方面,文献[16-17]建立了反射面结构的形状控制模型,并开展了调节作动器的优化布置研究,文献[18]通过仿真计算,发现优化方案可使天线型面误差降低80%以上.文献[19-20]对智能结构、智能控制系统在航天器上的应用提出了构想.
可以发现,国内相关研究主要处于型面测量与仿真分析阶段,与国外水平尚有一定差距.高分辨率遥感卫星是我国卫星发展的重要方向[21],本文以某遥感卫星天线的地面样机为研究对象,通过优化调节修复天线在不同工况下的热变形,验证调节方案的效果与可行性,为未来该项技术的在轨应用打下基础.
1 优化调节方案与算法
1.1 调节方案
天线型面优化调节方案由摄影测量系统、计算机与作动调节系统组成,如图1所示.摄影测量系统继承了文献[15]的相关技术,通过双相机拍摄天线阵面上的靶标点,计算得到靶标的位置坐标与拟合平面的型面精度,靶标的位置测量精度为10 μm.计算机集成了优化调节算法与作动器驱动软件,优化调节算法依据摄影测量的结果将调节量最优地分配到作动器上.作动调节系统为安装在天线阵面与框架之间的若干作动器,作动器位移输出精度高达1 μm.

图1 调节方案示意图Fig.1 Illustration of adjustment method
当天线阵面在温度环境作用下发生热变形,作动器在驱动软件控制下产生精密位移输出补偿阵面变形,达到修复型面精度的目标.
调节方案的关键在于各作动器调节量的确定,即在已知阵面各测点变形量的条件下,如何确定一组最优的作动器调节量,使得调节后的型面精度最高.由于各作动器的调节量对天线阵面的影响是相互耦合的,难以直观地通过阵面的变形来确定调节量,需要通过解耦方法与优化算法的研究,快速、准确地分配调节量,适应工程应用的需求.
1.2 优化算法
1.2.1 解耦方法
按照图1所示的调节方案,任意一个作动器的位移量均会引发整个阵面的变形,各作动器的调节作用是相互耦合的.为了实现各作动器之间的解耦调节,首先引入作动器影响函数的概念,即当某个作动器输出单位位移,而其他作动器位移为零时,在天线阵面各靶标点上产生的法向位移.作动器的影响函数与作动器位置、天线阵面刚度特性有关,可以通过型面测量系统实测得到.
假设天线背面共有m个作动器,天线阵面上共有n个靶标点,第j个作动器的影响函数在第i个靶标点的值为dxji,各个作动器的实际输出位移为x1,x2,…,xm,则第i个靶标点在作动器调节作用下产生的位移dsi为
(1)
式(1)成立的前提是作动器的输出位移为小位移,即x1~xm相对天线阵面的尺寸为小量,此时可认为天线的变形是各作动器影响作用的线性叠加,式(1)实际上将各作动器的耦合作用分解成了各影响函数的线性叠加.
1.2.2 目标函数
天线阵面优化调节的目标是在现有作动器的布局方式下,实现阵面的型面误差RMS值最小.
假设阵面发生热变形后的状态如图2所示,Pi为阵面上的第i个靶标点,P′i为靶标点在拟合平面上的投影.图中OXYZ为测量坐标系,以阵面的理想法向为Z轴方向,X、Y方向分别与阵面的短边、长边平行.
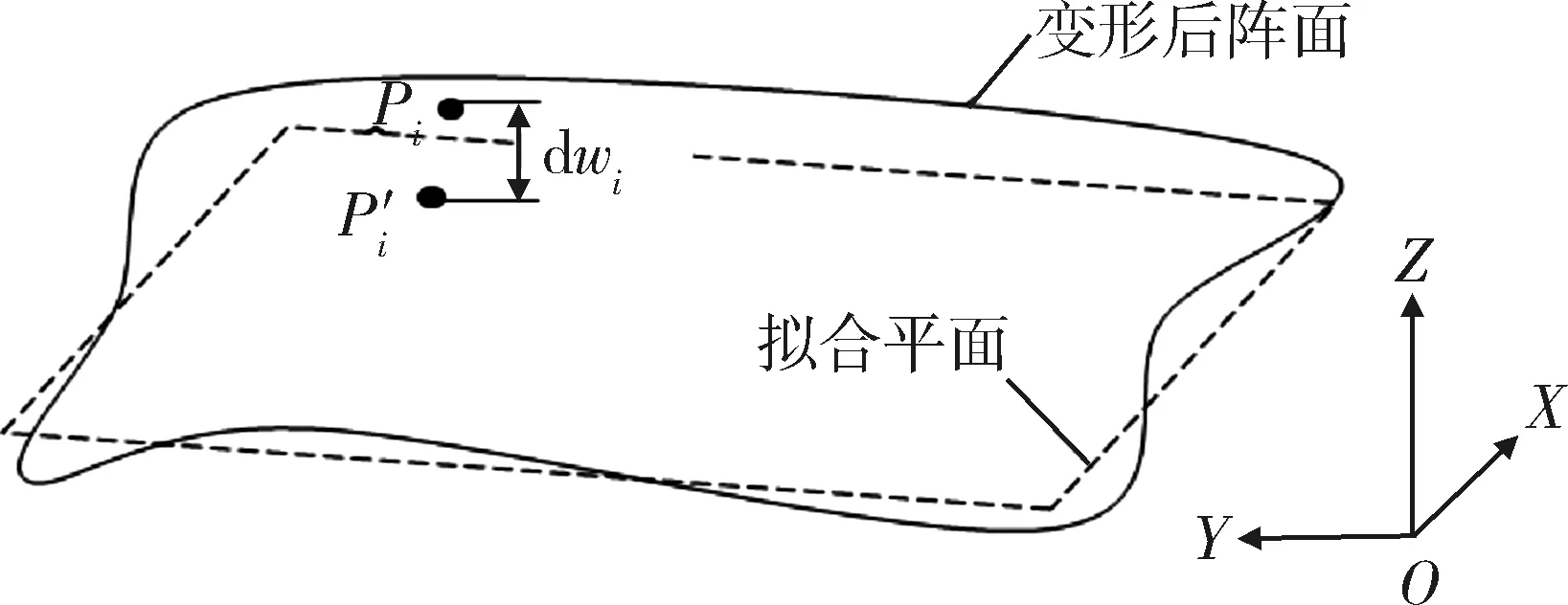
图2 变形后的天线阵面Fig.2 Deformed array surface
点Pi相对P′i的法向位移为dwi,则变形后的型面误差RMS值可表示为
式中,n为测点数量.
在一组作动器位移x1,x2,…,xm的调节作用下,靶标点Pi调节后的法向位移dw′i为
(2)
调节后的型面误差均方根E为
(3)
在确定的热变形工况下,式(3)中的dwi、dxji是固定值,可以通过型面测量系统的测量与计算得到,作动器的一组最优位移量xj(j=1,2,…,m)是待求解的变量,以实现最小的误差均方根E值.
1.2.3 最优位移量求解
采用最小二乘法求解使得均方误差E最小化的各作动器位移量,对式(3)关于xj求偏导数,并令各式等于0,即得到如下的线性系统:
HX=F
(4)
式中,H为m×m的方阵,X、F为1×m的列阵,矩阵元素如下:
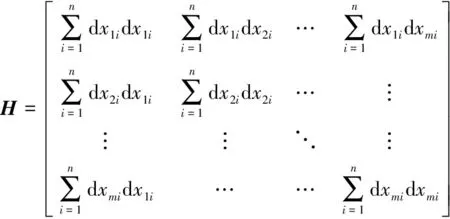
式(4)是典型的一阶线性方程组,采用经典的高斯消元法可以求得方程的解X,即一组最优的各作动器位移输出x1~xm,若将x1~xm代入式(3)可以反算出调节后的型面精度,为型面调节效果提供一个预测结果.
2 型面调节试验方法
2.1 模拟试验系统组成
为验证优化调节方法的可行性与效果,研制了由温度加载系统、型面测量系统、调节控制系统组成的型面调节模拟试验系统,如图3所示.模拟系统调节的对象是某阵列天线的缩比样机,该样机的阵面是厚度为10 mm的碳纤维蒙皮蜂窝板,阵面长1.4 m,宽0.8 m.

图3 模拟试验系统Fig.3 Configuration of simulation system
2.2 试验方案
天线型面调节模拟试验主要内容包括温度加载、型面测量、型面调节3个部分.
温度加载方案是在阵面背面的均布粘贴加热片,热控机柜采用PID算法控制加热片的输入功率,逐步达到加热片的目标温度.通过设定不同的加热片目标温度,可以实现天线阵面均匀温度、梯度温度的工况模拟.由于阵面的厚度较薄,温度在厚度方向上的变化可以忽略.
型面测量采用双目摄影测量方案,相关设备包括双相机、靶标与计算软件.天线阵面均布有140个靶标点,增加靶标点数量有利于充分反映阵面的型面精度,并能够减小摄影测量误差的影响.在温度加载后,双相机拍摄得到阵面上的靶标位置,坐标数据导入SA(spatial analyzer)软件进行数据处理与型面拟合,并计算得到靶标点相对拟合平面的法向位移,即图2中所示的dwi.
型面调节方案是在阵面背面等距布置12个作动器,作动器编号为1~12,各作动器在阵面上的布局如图4所示.

图4 作动器位置布局Fig.4 Layout of actuators
作动器底部固定在天线框架上,顶部通过柔性铰与阵面连接,如图5所示.

图5 作动器与柔性铰Fig.5 Actuator and flexible hinge
柔性铰采用高强度钛合金材料,通过释放作动器与阵面之间的转动自由度,避免调节过程中的强迫应力.
作动器的位移输出量由1.2节的优化算法确定,本试验中将算法编制为Matlab的GUI界面程序,程序读取型面测量得到的各靶标点法向位移,可以分配各作动器的位移量,由作动器驱动软件实现作动器的位移输出调节.
2.3 试验过程
在建立图3所示的试验系统后,首先测量12个作动器的影响函数,作为优化调节算法的必要输入.以第j个作动器为例,控制该作动器输出0.2mm位移,保持其他作动器不输出,测量得到n个靶标的法向位移dxj1,dxj2,…,dxjn,这组位移与作动器的输出位移之比即形成了第j个作动器的影响函数.
随后,模拟天线阵面在轨可能出现的3种温度工况.
1)均温50℃,天线阵面上温度分布均匀;
2)均温75℃,天线阵面上温度分布均匀;
3)梯度温度,沿阵面长度方向,温度由50℃线性增加到75℃.
在每个温度工况下,采用型面测量系统测量靶标相对拟合平面的位移,调用Matlab的GUI界面程序,分配各作动器的位移输出,实现型面调节.每次调节后采用型面测量系统复测天线的型面精度,验证调节效果.
单次调节试验的数据流如图6所示,图中矩形框表示软件,圆角矩形框表示数据.

图6 调节试验数据流Fig.6 Data flow of the adjustment experiment
3 试验结果
3.1 影响函数测量
在室温25℃状态下,实测得到12组作动器的影响函数,以图4中的1~6号作动器为例,输出影响函数形成云图,如图7所示.

图7 作动器影响函数云图Fig.7 Influence function nephograms of Actuators
从图7可以看出,越靠近作动器的位置,影响函数值越接近于1,作动器之间的影响区域存在交集,影响区域通过叠加可以覆盖整个阵面.
3.2 型面调节结果
系统装配完成后,在常温(25℃)状态下,不经作动调节,采用摄影测量系统对阵面初始型面误差进行测量,初始型面误差RMS值为0.042 mm,并得到误差云图如图8所示.
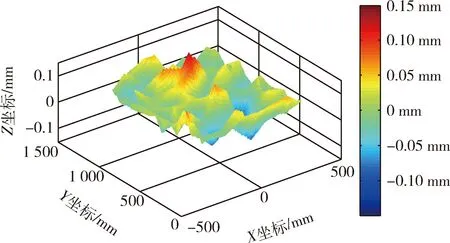
图8 初始型面误差云图Fig.8 Initial surface error nephogram
通过温度加载系统实现天线阵面上50℃均温、75℃均温与梯度温度3种温度工况.以50℃均温工况为例,阵面发生热变形后,测量靶标的点位数据,读入Matlab的GUI界面程序,程序分配了各作动器的最优位移输出,并预判调节后的型面误差RMS值与误差云图,程序计算结果如图9所示.
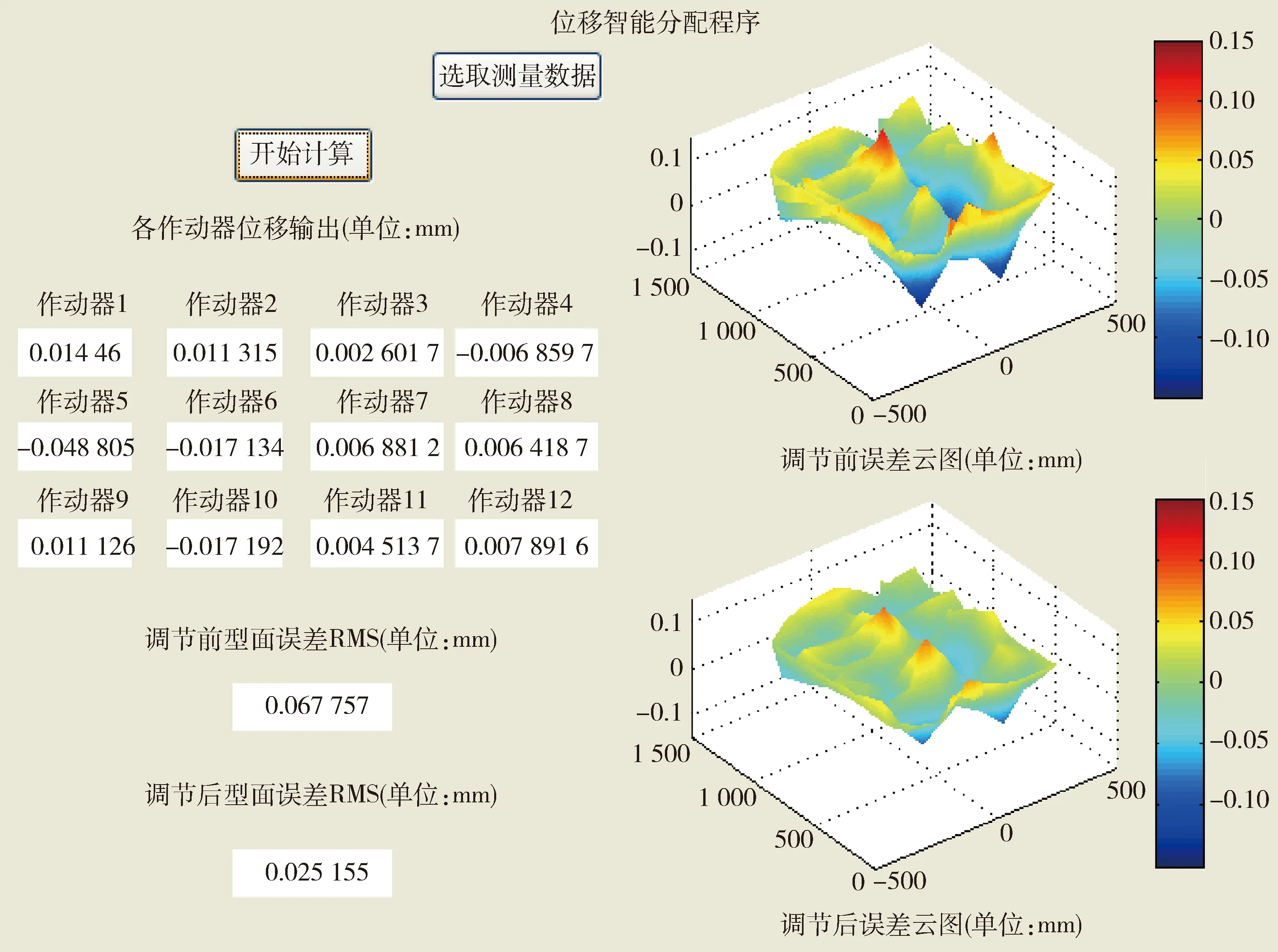
图9 GUI程序结果(均温50℃工况)Fig.9 Results of GUI program(50℃)
作动器调节完成后,采用型面测量系统复测天线的型面精度,得到各工况下调节前后的型面误差云图,如图10~12所示.

图10 均温50℃调节前后型面误差云图Fig.10 Surface error nephogram under 50℃
3种温度工况下的调节结果汇总于表1.
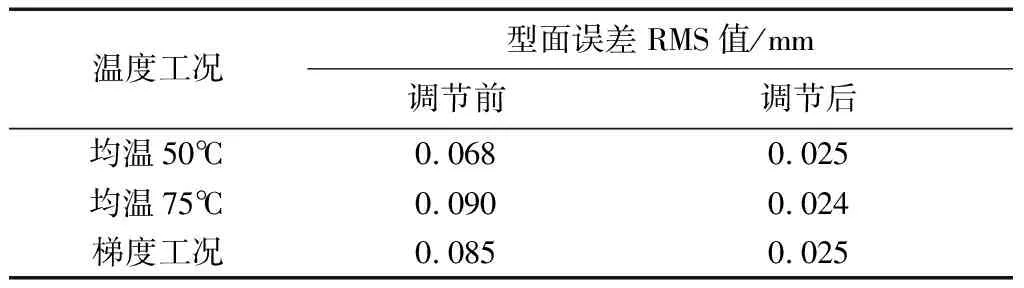
表1 型面调节结果汇总Tab.1 Summary of adjustment results
由表1可见,在各温度工况下,天线型面精度较常温状态明显降低.通过天线型面的优化调节,型面误差RMS值降低到了30 μm以内,相对调节前降低了60%以上.
由表1亦可看出,面对不同的温度工况,调节后的型面精度基本保持在25 μm左右,基本达到了本试验系统调节能力的极限,这是由作动器的数量与位置布局决定的.面向未来的大型星载天线,若要继续提升型面调节能力,需要从增加作动器数量、优化作动器布局的角度开展进一步研究.
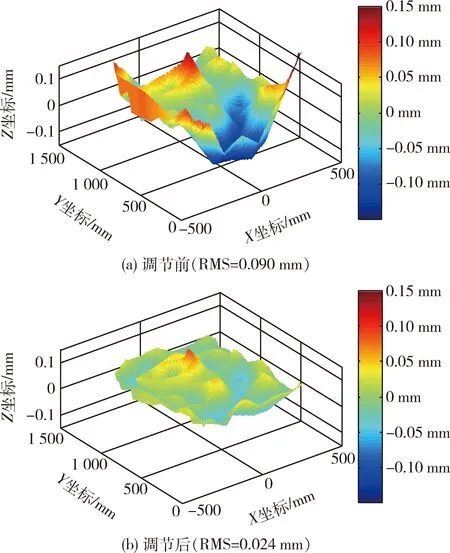
图11 均温75℃调节前后型面误差云图Fig.11 Surface error nephogram under 75℃
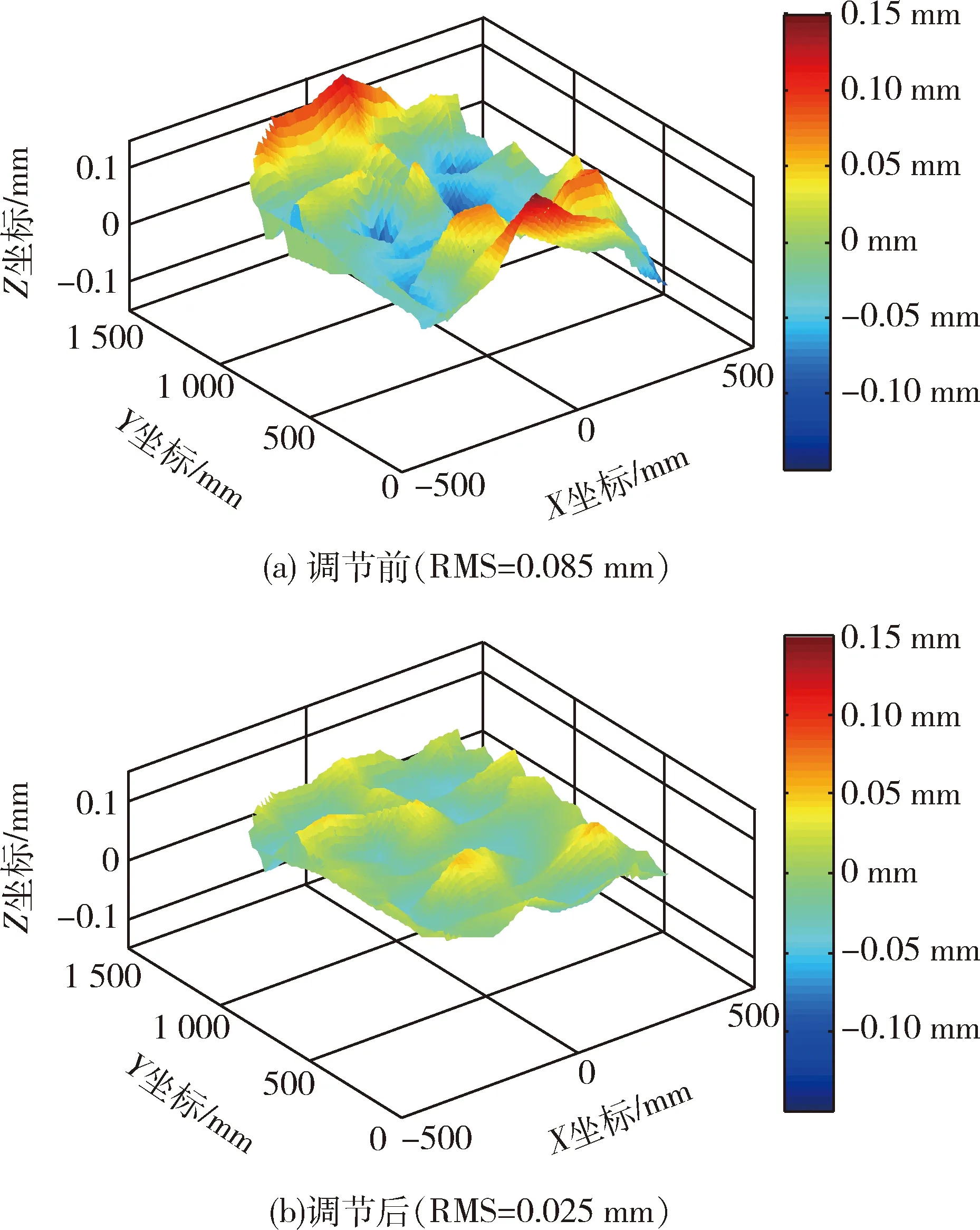
图12 梯度温度调节前后型面误差云图Fig.12 Surface error nephogram under gradient temperature
4 结 论
综合应用摄影测量技术、高精度位移作动技术与优化调节算法,本文实现了某星载天线地面样机的型面优化调节,有效修复了天线阵面在多种温度环境下的热变形,型面精度最优调节效果达到30 μm以内.相关研究内容可为天线型面优化调节技术在卫星型号上的应用打下基础.
