伺服电机速度的分数阶滑模容错控制*
2022-09-01秦明皇佃松宜
秦明皇, 陶 栩, 佃松宜, 郭 斌
1. 四川大学电气工程学院,成都市 610044 2. 四川三联新材料有限公司,成都市 610100
0 引 言
永磁同步电机系统因其高效率、高可靠性、易于维护等特点[1]而在高精度伺服系统中得到了广泛的应用.近几十年来,大量的文献探讨了永磁同步电机的控制方案,现有的控制方法主要可以分为两类,一是传统的线性控制方法,如比例积分微分控制器(PID)[2].该方法具有简单、参数设置方便,无需依赖系统模型等优点[3].然而,永磁同步电机是一个非线性、强耦合和多变量的系统[4],当控制系统受到外部干扰或电机内部参数变化的影响时,传统的比例积分控制方法无法达到实际要求.
二是非线性控制方法,如鲁棒控制[5],自适应控制[6-7],反步控制[8],神经网络控制[9]、模糊控制[10]和滑模控制(SMC)[11-14].在这些非线性控制方法中,滑模控制方法因其对某些内部参数变化和外部扰动的鲁棒性而闻名,在系统参数或模型不确定的情况下也可以保证较好的跟踪性能,已被广泛应用于永磁同步电机的速度控制.针对传统SMC存在的问题,提高其在跟踪和扰动抑制特性方面的性能,并减少抖振,许多方法被提出,包括改进滑模面[11],改进趋近律[12-13],高阶SMC和复合SMC设计[14]等.
分数阶滑模控制(FOSMC)[15]利用分数阶微积分构造其滑动面,与传统的整数阶滑模控制相比,积分和微分算子的额外自由度可以进一步提高控制器的性能,使其具有更快的响应速度,更小的跟踪误差.作为传统整数阶微积分到非整数阶的推广,分数阶的特点是衰减旧数据并存储新数据,数据可以更有判别性地使用,因此分数阶控制器更稳定或至少与整数阶控制器一样稳定.
到目前为止,已有许多控制器结合了分数阶微积分,最常见的是分数阶微积分与经典PID控制器的结合,表示为PIλDμ.由于引入分数阶微积分,PIλDμ控制器具备了更多优点,吸引了越来越多的研究人员在其不同的控制器中引入分数阶微积分,进一步使得更多的分数阶的控制器得到了发展,分数阶滑模控制器便是其中之一.分数阶控制器已被广泛证明比传统的整数阶微积分控制器具有更快的收敛速度和更好的稳定性.已广泛应用于复杂系统,如机器人、分数阶混沌系统等.本文将通过修改滑模面对传统SMC进行改进,得到一个FOSMC来控制PMSM的速度.
永磁同步电机伺服驱动系统在运行过程中很容易受到参数变化、负载扰动和非线性动力学的影响[16],进而导致控制性能的下降,严重时甚至导致故障的发生.因此,保证电机的可靠性和安全性,尽量减少电机故障对伺服驱动系统性能的影响,需要对电机进行容错控制.通常来讲,容错控制方法一般有基于数据驱动的智能控制方法和基于解析模型的传统方法.在实际情况下,关于电机故障的数据却不那么容易获得,因而基于解析模型的方法通常占据优先地位.从对故障的处理方式出发,容错控制还可分为主动容错控制和被动容错控制[17].被动容错控制利用鲁棒控制技术使整个闭环系统对某些确定的故障具有不敏感性,以达到系统故障后继续工作的目的.尽管滑模控制器对不确定性或故障具有一定的鲁棒性,然而前提是知道不确定性或故障的边界,通常情况下这种边界的先验知识是不被人所知道的,尽管可以通过增加滑模切换项的增益来提高鲁棒性,但这不可避免地会增加抖振,降低控制性能,无法满足高精度控制需求.更加有效的方式是采用主动容错控制方法[18],通过观测器对故障或不确定性进行估计,并将故障估计值反馈给控制器从而进行补偿.在文献[11]和[19]中,滑模观测器(SMO)和扩张状态观测器(ESO)分别被用于估计负载转矩,取得了有效的估计效果.在文献[20]中,SMO用于实时检测扰动量.相比于SMO和ESO,扰动观测器(DO)结构简单,便于实施而得到了广泛应用,在文献[21]中,DO被用于自适应控制器中补偿参数不确定性和输入饱和.在文献[22]和[23]中,为了提高电机速度控制的精度,DO为滑模控制器提供补偿项.在文献[24]中,非线性扰动观测器(NDO)用于补偿集总扰动.尽管扰动观测器已在许多场景得到了应用,但如何选择观测器增益仍然是一个值得研究的问题.传统NDO的增益通常为常数,不能根据实际情况做出改变,因而导致其收敛速度较慢.针对上述问题,本文将对传统的NDO增益进行改进,采用变增益的方式使之具备更快的收敛速度,从而及时对故障和不确定性进行有效补偿.
综上所述,本文将设计一种基于分数阶积分滑模和非线性扰动观测器的伺服电机容错控制方案,通过分析建立了电机故障模型,在此基础上讨论了电机容错控制方案,采用滑模控制提高了系统的鲁棒性,并利用分数阶理论对传统滑模控制进行改进,使之具备更快的响应速度,更小的稳态误差.为了对故障信号进行有效补偿,采用NDO对故障进行实时估计,并对观测器增益进行改进,使之对故障的观测速度更快,便于实时补偿,提高伺服驱动系统的控制性能,保证伺服系统的安全性和可靠性.
1 永磁同步电机数学模型
1.1 理想模型
本文以表贴式永磁同步电机为控制对象,选择同步旋转坐标系d-q下的数学模型.在理想情况下,永磁同步电机的定子电压的通用数学模型可表达为[25]:
(1)
定子磁链方程为:
(2)
式中,ψd和ψq分别为磁链在d轴和q轴分量;ud,uq和id,iq分别为d轴和q轴的电压和电流,R为定子电阻;np为极对数;ω为电机机械角速度;Lq和Ld分别为d轴和q轴的电感,对于表贴式永磁同步电机来说,Ld=Lq=Ls;ψ为永磁体磁链.
将式(2)代入式(1)可得定子电压方程为
(3)
进一步可写为:
(4)
电机的电磁转矩方程为

(5)
式中Te为电磁力矩.
电机机械角速度方程为
(6)
式中,TL为负载扭矩,J为转动惯量(kg·m2);bm为阻尼系数(Nm·s/rad).
将式(5)代入,最终可得到
(7)
1.2 电机故障数学模型
在电机的实际运行过程中,由于各种因素的影响,电机的电气和机械参数会随着操作条件的变化而变化,载荷转矩同样会随着实际操作而变化.这种变化会导致系统出现不确定性甚至故障的发生.为了减少这种不确定性或者故障的影响,需要对电机模型进行进一步分析.
本文暂时只考虑故障或不确定性发生在式(7)中.在电机运行过程中.由于电机长时间工作使得电机温度变化进而导致电阻发生改变,或由于环境磁场的变化使得永磁体受到影响,或温湿度变化导致摩擦系数变化,同时电机负载也为不确定项,将这些可能导致故障发生的因素考虑为一个整体附加项,因而电机模型可重写为
(8)
其中Fω为故障或不确定性项,其表达式为
(9)
Δρi(i=1,2)为不确定性变化项.
2 控制方案设计


图1 永磁同步电机控制系统总体结构图Fig.1 The overall structure diagram of the permanent magnet synchronous motor control system
2.1 分数阶滑模控制器
假设期望的电机机械角速度为ω*,定义跟踪控制误差为
eω=ω*-ω
(10)
根据分数阶理论,设计如下分数阶滑模面sω

(11)
式中,λ>0是待设计的滑模面参数;sgn()为符号函数;Dα(f(eω))表示对函数f(eω)做α阶微分,0<α<1.其计算公式为[28]:
(12)
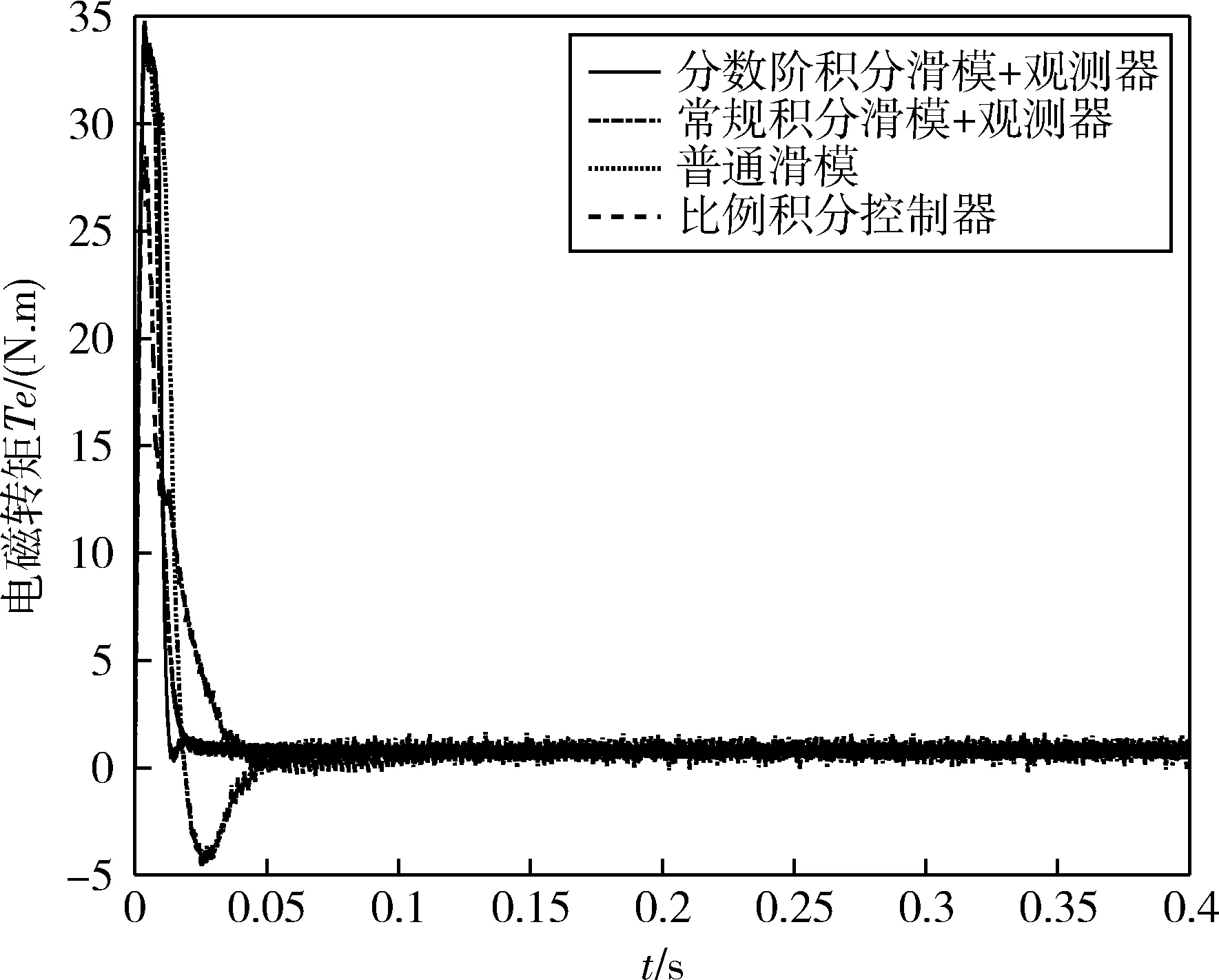
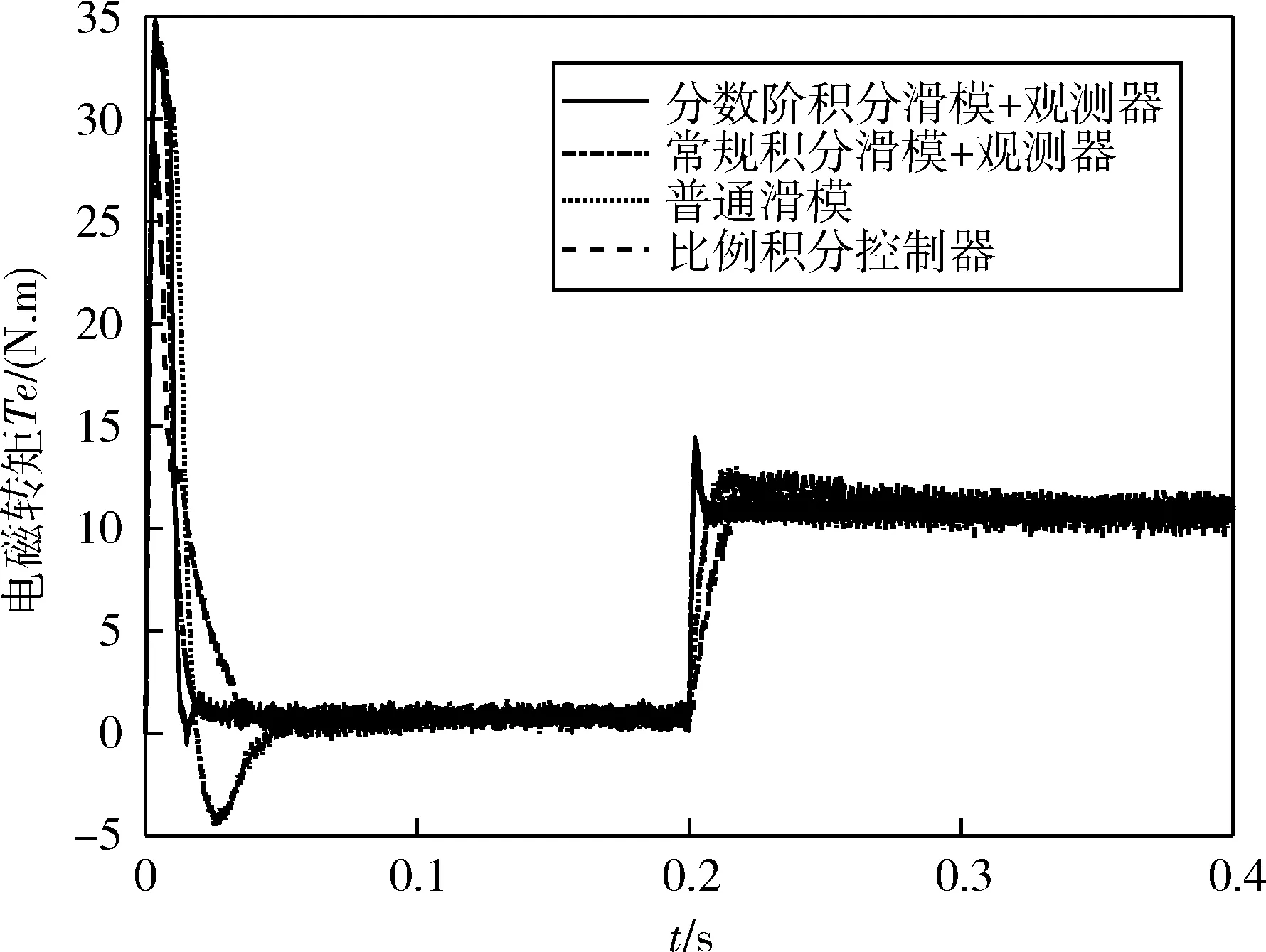
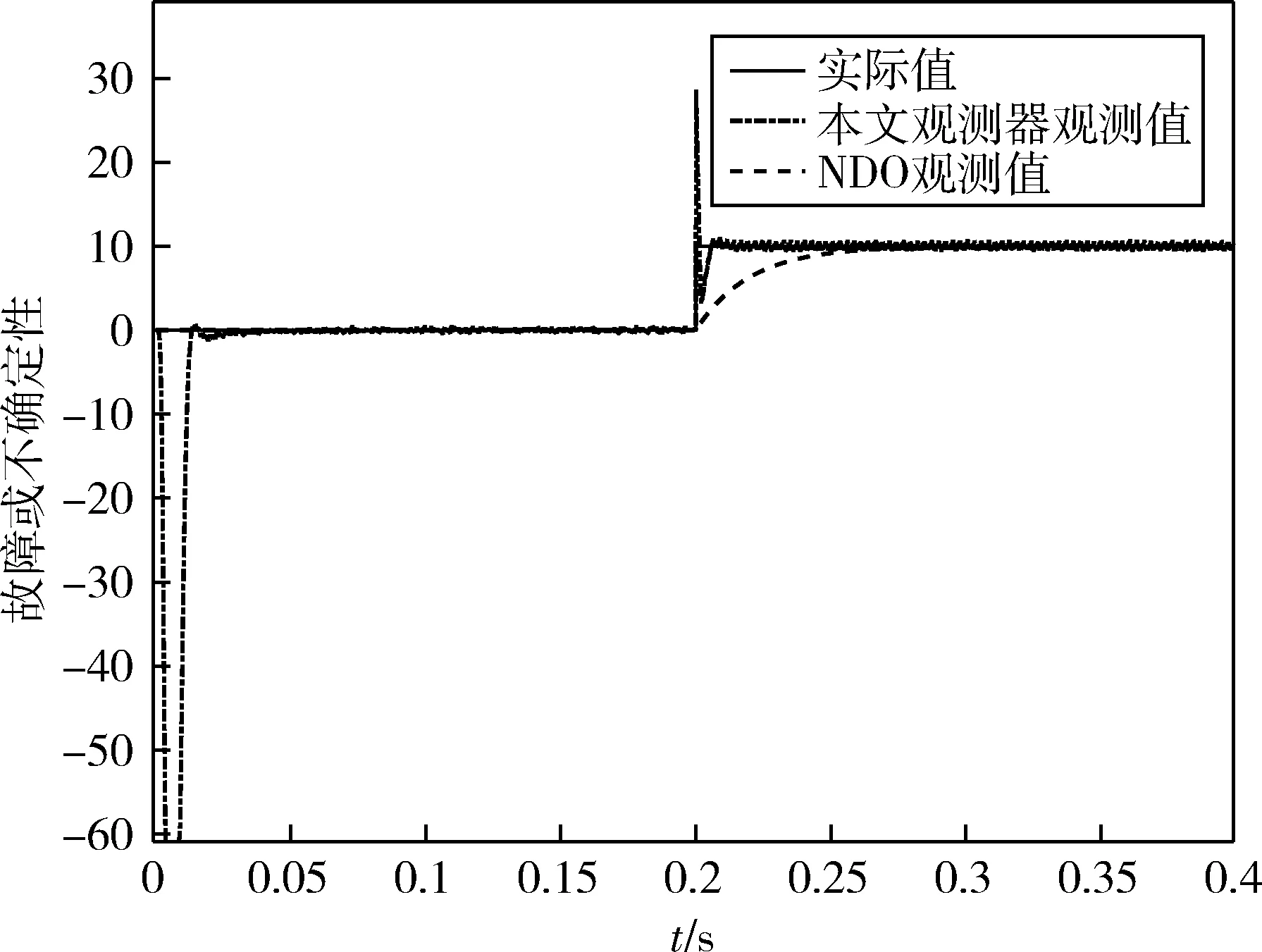
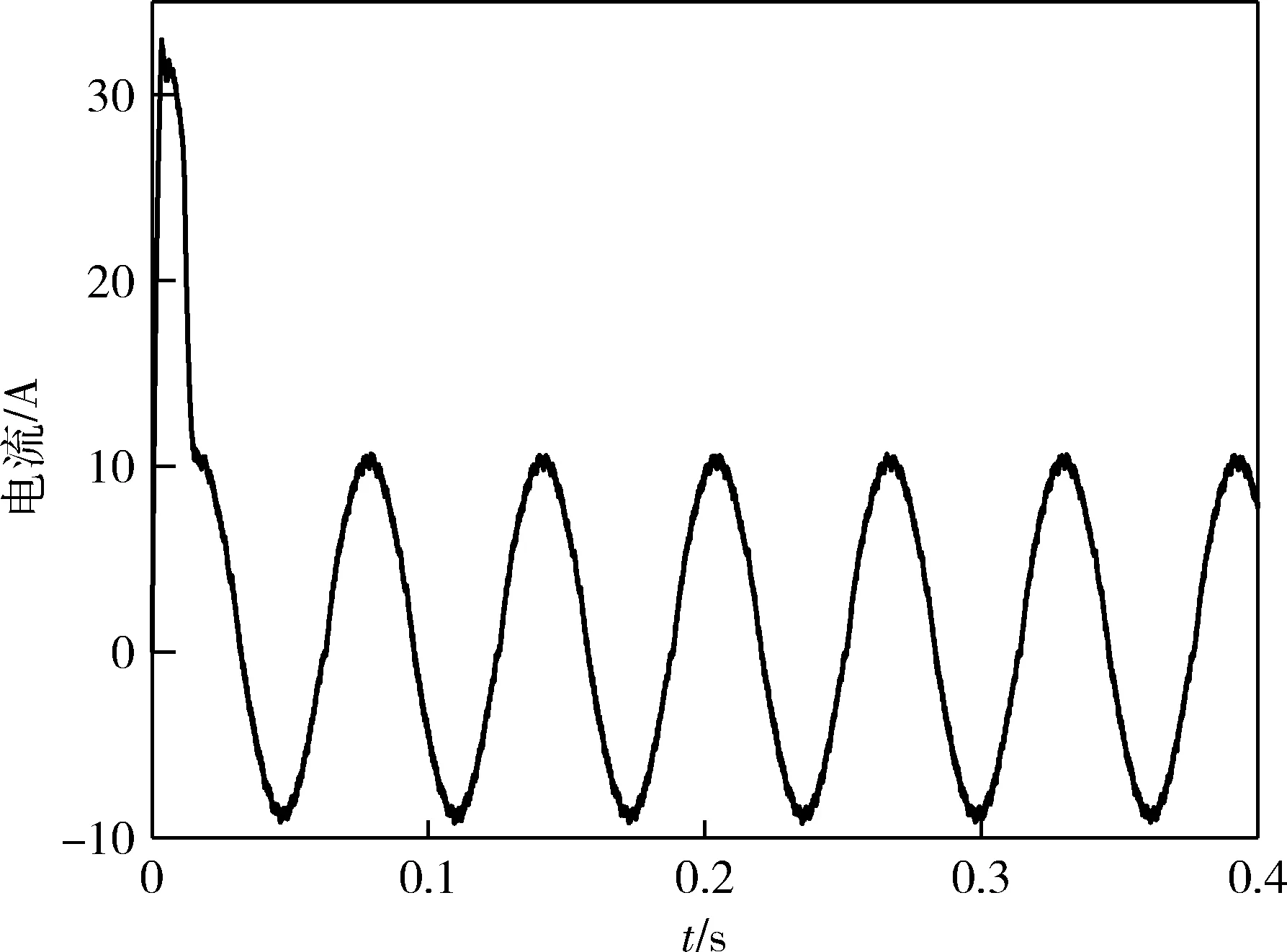
式中:Γ(n-a)表示gamma函数,0 sω关于时间求导,根据式(8)和(10)可得到 (13) 为了满足滑模条件,设计如下趋近率,其表达式为[29]: (14) 设计控制器为: (15) (16) (17) 根据李雅普诺夫稳定性理论,电角速度控制器是稳定的. (18) PI控制器设计为: (19) 式中,Kp和Ki分别为比例项和积分项增益,其表达式为 Kp=diag{kpd,kpq},Ki=diag{kid,kiq} (20) (21) 式中,Lω,p(ω)分别为观测器增益和待设计函数,并且具有如下关系: (22) 关于时间求导,并代入式(8)和式(21)可得: (23) 如何设计p(ω)是非常值得研究的问题,p(ω)通常被设计为线性的,Lω是一个常数.由于观测器增益是固定的,这导致观测器的收敛速度较慢.无法对故障或不确定性进行及时估计和后续补偿.受NGUYEN等[31]的启发,设计p(ω)为一个非线性函数,Lω也是非线性的,可以根据实际情况及时做出变化,加快观测器收敛速度. (24) 式中,m1,m2均为大于0的常数.在式(24)中,为了达到对故障的自适应效果,使得对不同程度的故障具有不同的响应,引入了电机角速度ω作为观测器增益的组成部分,可以更快地对故障进行估计.p(ω)和Lω由常量和电机角速度ω组成,当电机发生故障时,直接的体现便是电机角速度ω会发生变化,故障值越大观测器增益也更大,那么观测速度也就越快.图6、图10以及图14可以直观地看出效果. 引理2.对于给定的非线性扰动观测器,扰动估计误差有界. 证明.从式(23)可以得到 (25) 其中e是自然对数的底数.因此有 (26) 由于Lω=m1+m2ω2≥m1>0成立,-Lω的特征值为负,满足引理1的条件.当ω=0时-Lω的特征值取得最大值,式(26)有意义,定义: (27) 为了验证所提出的容错控制方法的有效性,使用MATLAB/Simulink对永磁同步电机驱动系统进行数值仿真.采样时间永磁同步电机参数如表1所示. 表1 永磁同步电机参数Tab.1 The parameters of permanent magnet synchronous motor 仿真主要分为3个部分,分别是(1)电机工作在正常情况下的控制器有效性验证(2)电机受到偏置故障影响的有效性验证(3)电机受到时变故障影响的有效性验证. 仿真中各模块的参数选取如表2所示. 表2 模块参数Tab.2 Parameters of each module 在正常情况下,本文方法与比例积分控制、传统线性滑模和整数阶积分滑模进行比较,图2为定负载情况下电机转速的控制效果.可以看出分数阶积分滑模和故障观测器的组合与PI控制、传统线性滑模控制器相比具有很大的优势,具有非常快的响应速度,几乎没有超调量的出现.与整数阶积分滑模的差别并不大,但由于分数阶引入的额外自由度,在控制器中引入了微分项,使得控制器具备一定的预测效果,因此更快的响应速度的到了体现. 图2 不同控制方法下电机转速控制效果Fig.2 Motor speed control effect under different control methods 图3为分数阶滑模的q轴电流输出,图4为本文方法与其他控制器的电机电磁转矩比较,这和电机速度控制是相互印证的,我们从中同样可以看出本文方法具有更快的响应. 图3 分数阶滑模控制下的q轴电流Fig.3 q-axis current under fractional sliding mode control 图4 不同控制方法下电磁转矩输出情况Fig.4 The output of electromagnetic torque under different control methods 图5为在正常情况下本文设计的观测器和传统的NDO观测器对故障或不确定性的观测效果,可以看出本文所设计观测器与传统的NDO观测器均能在有限时间内使观测误差收敛到零,值得指出的是在无故障情况下传统的NDO观测器似乎有着更好的观测效果,其观测值几乎没有太大的波动,而且在初始时刻不会有较大的偏离,但这也正体现出其对故障或不确定性的不敏感性或迟钝,无法及时对故障或不确定性做出有效估计. 图5 正常情况下不同观测器对故障的观测效果Fig.5 Observation effects of different observers on faults under normal conditions 在正常情况下验证了本文控制方法的有效性后,为了进一步验证伺服电机出现故障后本文所设计控制方案能否保证系统继续正常工作,对故障是否有一定的容忍性,在一定时刻对电机注入偏置故障,故障信号为:Fω=10,t>0.02 s. 图6展示了注入偏置故障前后不同控制器对电机转速的控制效果.在故障注入前,控制效果和正常情况下一致.当故障被注入后,由于故障的影响,电机转速立刻出现了较大偏差,本文所设计的分数阶滑模和观测器组合的方法与其他方法最终都可以使误差收敛到零是本文方法的收敛速度更快,传统滑模方法和比例积分控制器需要漫长的反应时间,在实际情况中这种情况是不可取的.传统的整数阶积分滑模由于在结构上与本文分数阶积分滑模在结构上相似,且也使用了观测器的故障观测值进行补偿,其控制效果也和分数阶积分滑模相似,但是本文方法具有更小的稳态误差. 图7为注入偏置故障分数阶滑模的q轴电流输出,图8为本文方法与其他控制器的电机电磁转矩比较.从图6、7可以看出,当偏置故障发生后,q轴电流立即发生变化,电机电磁转矩也是如此,这从另一个方面印证了本文控制器响应快速. 图6 注入偏置故障后不同控制方法对电机转速的控制效果Fig.6 Control effect of different control methods on motor speed after injecting bias fault 图7 注入偏置故障后q轴电流Fig.7 q-axis current after injection of bias fault 图8 注入偏置故障后不同控制方法下电磁转矩输出情况Fig.8 The electromagnetic torque output under different control methods after injection of bias fault 图9为注入偏置故障前后本文设计的观测器和传统的NDO观测器对故障或不确定性的观测效果,两种观测器均能正确有效地对故障值进行估计,然而本文地观测器具有更快地观测速度,能够及时对故障进行补偿,这对控制系统来说是非常重要的,具有重大意义. 图9 注入偏置故障后不同观测器对故障的观测效果Fig.9 The observation effect of different observers on the fault after injecting the bias fault 在3.2中,讨论了系统注入偏置故障后本文设计方法的容错性能,本文所设计控制方法取得了较好的效果,然而在实际情况中,偏置故障是一种相对简单的故障,要实现容错的目的也相对比较容易.在实际情况中,故障比较复杂,更多体现出时变的特性,为了尽可能仿真现实情况,此小节对系统注入时变故障,故障信号为幅度为10,频率为100 Hz的正弦信号,从仿真开始到结束一直存在. 图10为在时变故障下不同控制器对电机转速的控制效果.从图中可以看出,传统的滑模控制和比例积分控制器无法有效克服时变故障的影响,系统出现了振荡现象,无法满足控制要求. 图10 时变故障下不同控制方法对电机转速的控制效果Fig.10 The control effect of different control methods on motor speed under time-varying faults 本文方法即使在故障快速变化的情况下也能有效减少其对系统性能的影响,这得益于故障观测器对故障的及时有效估计,使得补偿得以顺利进行. 图11为时变故障下分数阶滑模的q轴电流输出,图12为本文方法与其他控制器的电机电磁转矩比较,其体现的意义与前文相同,在此不再赘述. 图11 时变故障下q轴电流Fig.11 q-axis current under time-varying fault 图12 时变故障下不同控制方法的电磁转矩输出情况Fig.12 The electromagnetic torque output of different control methods under time-varying faults 图13为本文观测器是传统NDO观测器对时变故障的观测效果,可以看出,即使故障变化较迅速,本文观测器仍能对其有效估计,而传统的NDO观测器由于增益不变,无法对变化稍快的故障进行估计. 图13 不同观测器对时变故障的观测效果Fig.13 Observation effects of different observers on time-varying faults 本文提出了一种基于NDO和分数阶积分滑模容错控制方案.在永磁同步电机驱动应用中,受各种因素的影响,系统可能会出现故障,降低系统的整体控制性能,因此提出了一种非线性增益的NDO,对故障进行及时有效地估计并在控制器中进行补偿,以提高表贴式永磁同步电机驱动器的容错能力.基于分数阶理论设计了分数阶积分滑模控制器,使系统具有更快的响应速度.分别在正常情况下和系统故障情况下,通过MATLAB/Simulink软件包验证了提出的基于NDO和分数阶积分滑模容错方案的有效性.仿真结果表明,该容错控制方法可以有效保证系统安全性和可靠性,提高同步电机速度跟踪控制能力、具有快速动态响应、更小的稳态误差等性能.



2.2 观测器设计


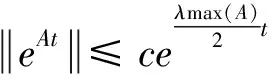

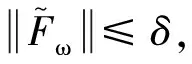
3 仿真结果

3.1 正常情况



3.2 偏置故障


3.3 时变故障



4 结 论
