大型挠性天线的主动振动抑制与相对位置控制

冯 骁，汤 亮，关 新，郝仁剑，张科备

1. 北京控制工程研究所, 北京 100094 2. 空间智能控制技术重点实验室, 北京 100094

0 引 言

随着测绘分辨率需求的不断提高，微波遥感卫星越来越多地采用长基线的雷达干涉仪进行遥感观测[1-2].一方面，在这些任务当中，需要以高精度、高稳定度保持两个天线阵列的相对位置. 另一方面，随着天线基线长度的增加，天线载荷整体的挠性日益显著，而由于空间结构的阻尼比低，天线受扰产生的挠性振动衰减缓慢，严重影响载荷的有效工作. 同时，挠性天线的振动也会引起星体姿态的晃动，威胁任务安全. 因此，需要研究大型挠性天线的振动抑制与相对位置控制方法，以实现载荷和卫星的高效、稳定工作.

作为本文工作的基础，对相关文献和研究工作进行简要分析. 挠性卫星的姿态控制与振动抑制一直是航天控制研究的热点，相关研究广泛而深入. 卫星的姿态控制系统一般采用安装在刚性星体上的姿态传感器和执行机构控制卫星的姿态运动，将挠性天线载荷作为挠性附件处理. 为避免姿态控制系统与附件的挠性模态发生耦合作用，往往将控制带宽设计为比系统的一阶挠性模态频率(基频)低一个数量级，即采用频率隔离法[3]. 但是，随着卫星及载荷基频的下降，采用频率隔离法将限制系统的控制性能. 为提高系统控制性能，必须在设计中考虑挠性的影响.

对具有显著挠性影响的航天器，在不改变卫星姿态控制系统传感器与执行机构配置的前提下，可以采用两种思路提高控制性能. 一方面，可以减少姿态机动对挠性振动的激发，另一方面，可以利用姿态控制系统进行振动抑制. 前一类方法根据挠性参数设计姿态机动控制力矩序列，使得星体姿态到达目标的同时，各指令激发的附件挠性振动相互抵消[4]；或对机动参考轨迹进行滤波，去除挠性频率处的成分，避免对挠性模态的能量输入[5-6]. 该类方法的难点在于如何设计成形滤波器，使其抑制效果对模型参数不敏感.同时，该类方法较难抑制非机动因素导致的振动.后一类方法通过适当提高姿态控制回路的带宽，并对低阶挠性模态进行相位稳定，为低阶模态提供一定的阻尼作用[7].针对挠性模态参数具有不确定性时的鲁棒姿态控制问题[8]，以及输入饱和与执行机构故障时的姿态控制与振动抑制问题[9]，也有学者进行了研究. 该类方法的应用难点在于如何在执行机构和传感器噪声、对象不确定性、时延等因素的影响下设计具有足够控制性能和鲁棒性的控制回路. 上述方法在控制航天器姿态的同时，通过航天器姿态与挠性振动的动力学耦合进行振动抑制，若能采用一定方法直接地控制挠性模态运动，则能够更好地实现控制目标.

直接对挠性载荷、附件进行振动抑制的方式可分为被动和主动两种. 在SRTM任务中，针对60m桁架在喷气姿态控制中的振动问题，JPL的研究人员设计了一套安装在桁架根部的被动阻尼系统，提出将应变能量集中在根部进行消除[2]. 但是，由于材料特性在轨变化失效，该系统被再次锁紧，最终任务依靠其他子系统的设计裕量完成. 主动振动抑制系统通过传感器和执行机构对振动进行测量和控制，系统构成相对复杂，但具有较好的控制性能和灵活性.目前，受到较多研究的是采用压电材料进行分布式振动测量与控制的智能结构[10-13]，以抑制机动造成的挠性振动为主，有较好的控制性能. 该方案在实现中的问题在于需要在挠性载荷、附件表面铺设大量压电片，需要较多布线和结构设计工作. 文献[14]提出在挠性附件根部安装旋转执行机构，利用附件端部安装的传感器测量振动，进行集中式的振动抑制，取得了很好的控制效果，其仅使用少量执行机构和传感器，是一种较为实用的方法.

相比文献[14]中以振动抑制为主的控制任务，大型挠性天线还需要精确的相对位置控制. 因此，本文提出一种以相对位姿测量相机为传感器、以文献[15]提出的主动指向超静平台为执行机构的大型挠性天线主动振动抑制与相对位置控制系统. 其中，相对位姿测量相机能够对天线末端的位移进行高精度测量，主动指向超静平台能够提供宽带宽的精稳执行能力.

在该系统中，相机测量天线末端的相对位移，而主动指向超静平台在天线根部施加控制作用，控制输入和输出间具有挠性环节，因此控制问题具有异位控制的特点. 在挠性结构的共位控制中，被控对象呈无源性，控制系统与结构间有稳定的耦合作用，易于进行控制[16]. 而在异位控制中，控制系统与挠性模态易发生不稳定的耦合作用，例如，对弱阻尼结构，比例-微分控制仅能采用较低的带宽，否则将使挠性模态不稳定[17]. 采用LQG方法可以在模型较精确的条件下实现高性能的异位控制，但是其原理是对弱阻尼极点进行对消，因此对模型不确定性的鲁棒性较弱[17]. 对于存在一定频率不确定性的异位控制问题，文献[18]提出采用包括非最小相位滤波器在内的广义结构滤波器对挠性模态进行鲁棒稳定. 到目前为止，异位控制仍是柔性结构控制中的一个重要问题[19]. 上述结果对控制设计具有指导意义，同时，对于具体的系统，还需要设计人员根据系统的特性进行控制器设计. 本文针对研究的系统，提出了一种能够实现挠性天线载荷振动抑制与位置控制的控制器，其能够为天线的一阶挠性模态提供阻尼作用，同时保持高阶模态的稳定. 控制器具有积分控制+结构滤波器的形式，也可被解释为比例-积分-微分控制器+低通滤波器. 进一步，考虑星体与载荷的耦合运动，在天线载荷控制回路的基础上设计了星体-载荷两级控制. 为了说明设计控制器的有效性，通过数学仿真和全物理仿真试验对控制系统和控制律设计的有效性进行了考核.

本文后续安排如下：第2节简要介绍大型挠性天线及主动振动抑制与位置控制系统的组成，并建立挠性天线载荷的动力学模型. 第3节提出对挠性天线进行振动抑制与位置控制的控制器，并通过数学仿真考核控制律设计的有效性. 第4节建立星体-载荷的耦合动力学模型，在天线载荷控制器的基础上设计星体-载荷两级控制，并对两级控制进行数学仿真. 第5节介绍大型挠性天线控制的全物理仿真试验，包括系统组成、测试与试验结果. 最后，基于数学仿真与试验测试结果给出结论.

1 挠性天线载荷动力学模型

挠性天线载荷的示意图如图1(a)所示. 天线载荷由天线支撑臂和天线阵列组成，由于支撑臂长度长、天线阵列质量大，天线载荷的固有频率低，需要进行主动振动抑制. 为了定量测量天线载荷的振动情况，在天线阵列中心安装靶标，在载荷安装点附近安装相机，通过相机对靶标的拍摄与位姿解算得到天线阵列中心的运动.为了有效抑制天线载荷的挠性振动，在天线支撑臂末端与载荷安装点间安装主动指向超静平台作为执行机构. 由于天线载荷的主要弹性变形集中于天线支撑臂根部，在此处布置执行机构能够最为有效地抑制挠性振动. 为描述系统运动，建立坐标系oaxayaza，与载荷安装点固连.

图1 挠性天线载荷及提出的传感器、执行机构配置示意图Fig.1 Schematic of flexible antenna with the proposed configuration of sensors and actuators

主动指向超静平台的示意图如图1(b)所示，其由3组共6条支腿构成. 每条支腿通过球铰与上平台连接，通过万向铰与下平台连接. 每条支腿在轴向可等效为一个弹性原件、一个阻尼原件和一个主动力原件的并联. 实际实现时，为了消除铰链间隙、摩擦等非线性因素，一般用柔性铰实现球铰功能，用膜簧等效实现万向铰与支腿轴向刚度功能. 无主动控制力时，超静平台可被视为一个挠性连接结构. 六条支腿的主动控制力则可被等效为作用于天线载荷的六维力、力矩.

在本文中，考虑挠性天线在图1(a)中oaxaya面内的振动，其他方向的振动同样可以使用本文中的方法进行控制. 当天线载荷在oaxaya面内振动时，变形以天线支撑臂根部绕za轴的弯曲为主，并导致天线阵列中心沿ya方向振动. 因此，为使系统具有较强的可控性和可观性，由相机测量天线阵列中心沿ya轴的位移，并通过主动指向超静平台沿za轴输出的力矩对系统进行控制.

将主动指向超静平台与天线载荷视为一个固定边界的挠性结构，同时考虑各支腿的主动力，则挠性天线载荷的动力学模型可根据有限元方法写为[20]

(1)

其中，η为模态坐标列阵，2ζΩ为模态阻尼矩阵，Ω2为模态刚度矩阵，Φr为结构在主动指向超静平台的上平台处绕za轴的转动模态矩阵，ta为主动指向超静平台输出的绕za轴的控制力矩. 2ζΩ与Ω2的表达式如下：

其中，n为选取的模态数，ωi和ζi分别为第i阶模态频率和阻尼比.

天线阵列中心沿ya方向的运动可用模态坐标表示为

y=Φtη

(2)

其中，Φt为天线阵列中心处的平动模态矩阵.

综合式(1)和式(2)，可以将挠性天线载荷的动力学模型写为如下标准的状态空间形式：

(3)

为进行仿真分析，参考SWOT等航天器构型[1]，通过合理选择天线载荷和主动指向超静平台的尺寸、物理参数，得到如表1所示的模型参数.

表1 有限元方法得到的挠性天线载荷参数Tab.1 Parameters of flexible antenna obtained via finite element method

2 控制器设计与数学仿真

2.1 主动振动抑制与位置控制

系统的被控量为支撑臂末端天线阵列中心的位移y，控制输入为主动指向超静平台产生的控制力矩ta，系统的输出与输入之间具有天线支撑臂这一挠性环节，因此，控制器设计为一个异位控制问题. 异位控制中，挠性模态与控制系统易产生不稳定的耦合作用，其控制律设计相比共位控制问题更为困难.

通过对该系统的研究，发现具有如下形式的控制律能够有效实现对一阶挠性振动的主动抑制和对天线阵列中心位置的主动控制：

(4)

其中，s为拉普拉斯变量，kc为控制器系数，ωz为控制器零点频率，ζz为控制器零点阻尼比，ωp为控制器极点频率，ζp为控制器极点阻尼比. 控制器零点的频率略低于一阶模态频率，控制器极点频率在一阶模态频率之上，且具有较大阻尼比. 采用该控制律时，控制回路的框图如图2所示.其中，yd为天线阵列中心沿ya方向的期望运动，控制输入ta和输出y的定义如式(1)和式(2)所示，x、y、A、B、C、D的定义如式(3)所示，控制器各参数的定义如式(4)所示.针对本文研究的系统，控制器各参数取值如表2所示.

表2 挠性天线主动振动抑制与相对位置控制控制器参数Tab.2 Parameters in the active damping controller for the flexible antenna

图2 挠性天线载荷控制回路框图Fig.2 Flexible antenna control loop

挠性天线主动振动抑制与位置控制的控制回路分析如图3所示.现对式(4)中控制器的结构进行分析. 该控制器可被视为一个积分控制器与结构滤波器的串联. 由于图1所示的挠性天线系统具有固定边界，系统表现出刚度特性，若要天线阵列中心稳定在非零的指令位置，则必须要施加一个非零的控制力矩，积分控制的作用就是在位置控制中提供该力矩. 结构滤波器的主要作用是在控制回路的合适频率处调整开环传递函数的幅值和相位，镇定不稳定的挠性模态.

由图3(a)的Nichols图可见，结构滤波器的零点提供的超前相位使一阶挠性模态进入相位为0°附近的正阻尼区域[14]，对该阶模态进行相位稳定，增加其阻尼比，实现主动阻尼的效果；同时，保持二阶以上模态的增益和相位稳定，保证系统的稳定性. 由图3(b)的根轨迹可见，通过适当地选择零极点位置和增益，可以使一阶模态在频率基本不变的同时，阻尼比由0.005增大至0.5左右，实现了主动振动抑制的目标.

图3 挠性天线载荷控制回路分析Fig.3 Control analysis for the flexible antenna control loop

由于比例-积分-微分控制器的结构是一个原点处的极点加两个共轭零点，式(4)还可以被视为一个比例-积分-微分控制器与一个二阶低通滤波器的串联. 由于挠性天线的一阶模态振型主要为主动指向超静平台的偏转及天线支撑臂的一阶弯曲，近似于一个带有扭转弹簧的失重单摆，直观上采用比例-积分-微分控制能够较好地控制一阶模态. 同时，比例-积分-微分控制对高阶模态有相位超前和幅值放大作用，需要低通滤波器重新稳定高阶模态.

2.2 数学仿真结果

根据图2所示框图和表1、表2中的参数，对主动振动抑制和位置控制两种情况进行了数学仿真，其结果如图4所示.

主动振动抑制的仿真结果及其与无控自由振动仿真结果的对比如图4(a)所示. 天线阵列中心的初始位移约0.1 m，若不采用主动振动抑制，经过2 000 s的自由振动，天线阵列中心的位移仍可达到0.01 m左右，衰减非常缓慢. 采用主动振动抑制时，振动在1～2个振动周期、约100 s以内即被完全衰减. 考虑到自由振动2 000 s时仍有可观的振动幅值，采用主动振动抑制时，挠性天线受扰后恢复工作状态的快速性指标提升了1～2个数量级.

图4 挠性天线载荷振动主动抑制与位置控制数学仿真结果Fig.4 Numerical simulation of active damping and position control of the flexible antenna

3 星体-载荷两级控制

在挠性天线载荷主动振动抑制与相对位置控制的基础上，考虑星体-载荷的两级控制.

带有挠性天线载荷的卫星示意图如图5所示，挠性天线载荷安装在刚性星体上，星体坐标系obxbybzb固连于整星质心. 为简化推导，假设obxbybzb各轴与oaxayaza各轴平行. 根据中心刚体+挠性附件的航天器模型，星体-载荷的耦合动力学模型可写为[20]

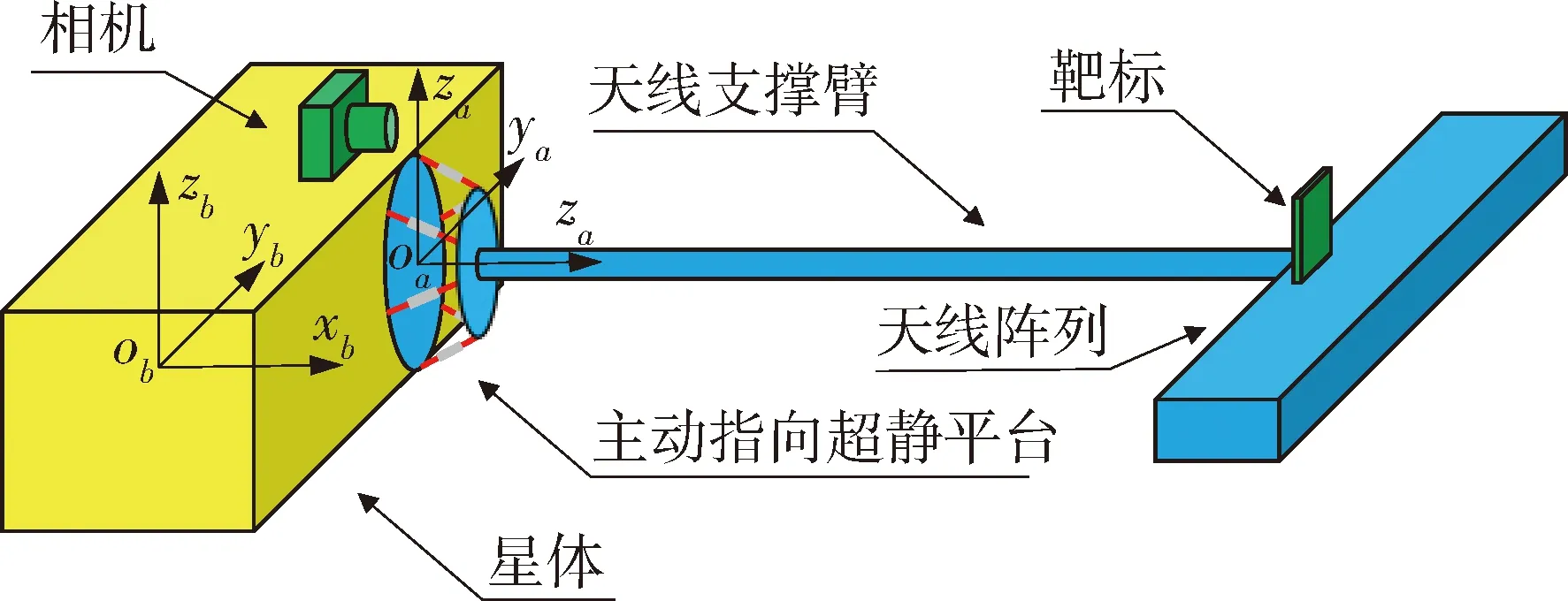
图5 带有挠性天线载荷的卫星示意图Fig.5 Schematic of spacecraft with a flexible antenna

(5)

或

(6)

其中，

I为整星绕zb轴惯量，θ为星体绕zb轴的姿态角，Fr为挠性天线载荷的转动耦合系数矩阵，tb为星体的控制力矩，其他变量的定义与式(1)中相同. 在使用单轴气浮台的地面试验中，星体模拟器的平动被约束，仅能做定轴转动，此时，虽然转动轴不通过系统质心，但系统动力学方程仍具有式(5)的形式.

式(6)可被写为如下的标准状态空间形式：

(7)

C=blkdiag{1,Φt,1,Φt}，D=0

在仿真中，挠性天线绕zb轴的惯量约为34 600 kg·m2，星体惯量则取为80 000 kg·m2，因此整星惯量I取值为114 600 kg·m2. 耦合系数矩阵Fr的取值如表3所示.

表3 模态耦合系数Tab.3 Modal parameters for rigid-flexible coupling

星体-载荷两级控制系统的框图如图6所示. 其中，θd表示星体姿态机动的期望轨迹，I、tb、θ的定义如式(5)所示，x、y、A、B、C、D的定义如式(7)所示，其余变量的定义与第1、2节中相同. 对星体姿态，采用比例-微分控制，并根据规划的角加速度计算前馈力矩进行补偿. 将星体姿态控制回路带宽选为0.000 5 Hz，阻尼比选为0.707，考虑整星惯量，有kp=1.13，kd=509.对挠性天线载荷控制回路，使用第2节提出的控制器进行控制. 由于星体控制回路与载荷控制回路的耦合作用，在采用相同的控制参数时，载荷控制回路的根轨迹与极点位置相比不考虑星体姿态运动时有所变化，但其基本形态一致.

图6 星体-载荷两级控制回路框图Fig.6 Two-stage control loop for the coupled spacecraft-antenna dynamics

采用星体-载荷两级控制，进行整星机动的仿真结果如图7所示，机动采用1-cos型轨迹. 在启用与不启用主动振动抑制控制器两种情况下，天线阵列中心的位移情况如图7(a)所示，其对比结果与不考虑星体运动时基本一致，可见设计的主动振动抑制控制器在考虑挠性天线与星体的动力学耦合时仍是有效的.星体姿态角的仿真结果如图7(b)所示. 不启用主动振动抑制控制器时，星体姿态角在机动过后有会有较长时间的振荡，主要由挠性天线和星体姿态的耦合振动引起. 启用主动振动抑制控制器时，由于挠性天线的振动被很快抑制，星体的姿态角振荡也被快速抑制. 因此，设计的星体-载荷两级控制能够有效抑制天线载荷的挠性振动，消除星体姿态角的振荡，使载荷和卫星在机动过后快速到达工作状态.

图7 星体姿态机动时有无主动振动抑制效果对比Fig.7 Comparison between active damping and free vibration

4 全物理仿真试验

为对设计的控制方案和控制律进行测试，搭建了大型挠性天线主动振动抑制与位置控制全物理仿真试验系统，进行了试验系统的测试和控制试验.

4.1 试验系统组成

全物理仿真试验系统的组成如图8所示. 在单轴气浮台和花岗石平台上开展仿真试验，单轴气浮台用于模拟星体姿态运动，天线支撑臂和天线阵列模拟器通过气足安放在花岗石平台上，模拟空间微重力环境. 天线支撑臂(包含部分惯量模拟件)与单轴气浮台间通过主动指向超静平台连接. 相机通过拍摄测量靶标确定天线阵列模拟器相对单轴气浮台的运动. 试验中还使用了激光测振仪以及主动指向超静平台各支腿的涡流位移传感器辅助测量振动情况. 其中，激光测振仪测量天线阵列模拟器上测试点的线速度(通过数据处理可得到位移和加速度)，涡流传感器测量各支腿长度的变化.

图8 试验系统组成示意图Fig.8 Schematic of the experimental setup

由于试验条件的限制，试验系统的质量参数和挠性参数与仿真中所采用的均有一定差别. 其中，挠性天线载荷的一阶频率约0.11 Hz.但是，试验系统的基本特征与理论分析和仿真中的对象一致.

4.2 试验系统测试

对天线阵列位移的准确测量是实现振动抑制和精确位置控制的关键. 为了测试相对位姿测量相机在振动条件下的性能，对天线阵列模拟器施加初始扰动，将相机和高性能激光测振仪的测量值进行对比. 测试结果如图9所示，可见相机的测量结果与激光测振仪的一致性较好，可以应用于振动测量与控制.

图9 测量相机与激光测振仪一致性测试Fig.9 Consistency of the camera measurement with the laser vibrometer

4.3 控制试验结果

试验中首先对星体固定的工况进行了测试，对应本文第1、2节中研究的情况. 主动振动抑制的试验结果如图10(a)所示，无主动振动抑制时，天线受扰后振幅衰减至1 mm以下的时间大于1 000 s，而采用主动振动抑制后，振动能够在2～3个振动周期内快速衰减，快速性指标提升1～2个数量级. 其中，“端部测量”表示以测量相机或激光测振仪测量的天线端部(天线阵列模拟器)位移为反馈，而“根部测量”表示以主动指向超静平台涡流位移传感器测量的支杆长度变化为反馈. 由试验结果可见，采用端部测量的振动抑制效果好于采用根部测量时的效果. 各情况下的振动衰减时间与实测阻尼比如表4所示.

表4 振动抑制效果对比Tab.4 Comparison of the settling time and measured damping factor

星体固定时，天线端部位置控制的试验结果如图10(b)所示，位置指令为5 mm阶跃指令，位置控制响应的上升时间约5 s，调节时间约15 s.可见，位置控制能够为天线载荷带来快速、准确的主动控制和调节能力.

试验中对星体气浮的工况也进行了试验，对应本文第3节中研究的情况. 在相同的整星机动过程中，对比了无主动振动抑制与使用主动振动抑制时天线载荷的振动情况. 试验结果如图10(c)所示. 可见，星体机动将激起天线载荷的振动，而使用主动振动抑制可快速抑制振动，使得载荷在机动后快速进入工作状态. 图中，使用主动振动抑制时，载荷无振动，但有较大的准静态位移，这是由于试验中为实现主动振动抑制，通过主动指向超静平台添加了一定量的负刚度控制，使得连接刚度有所降低.

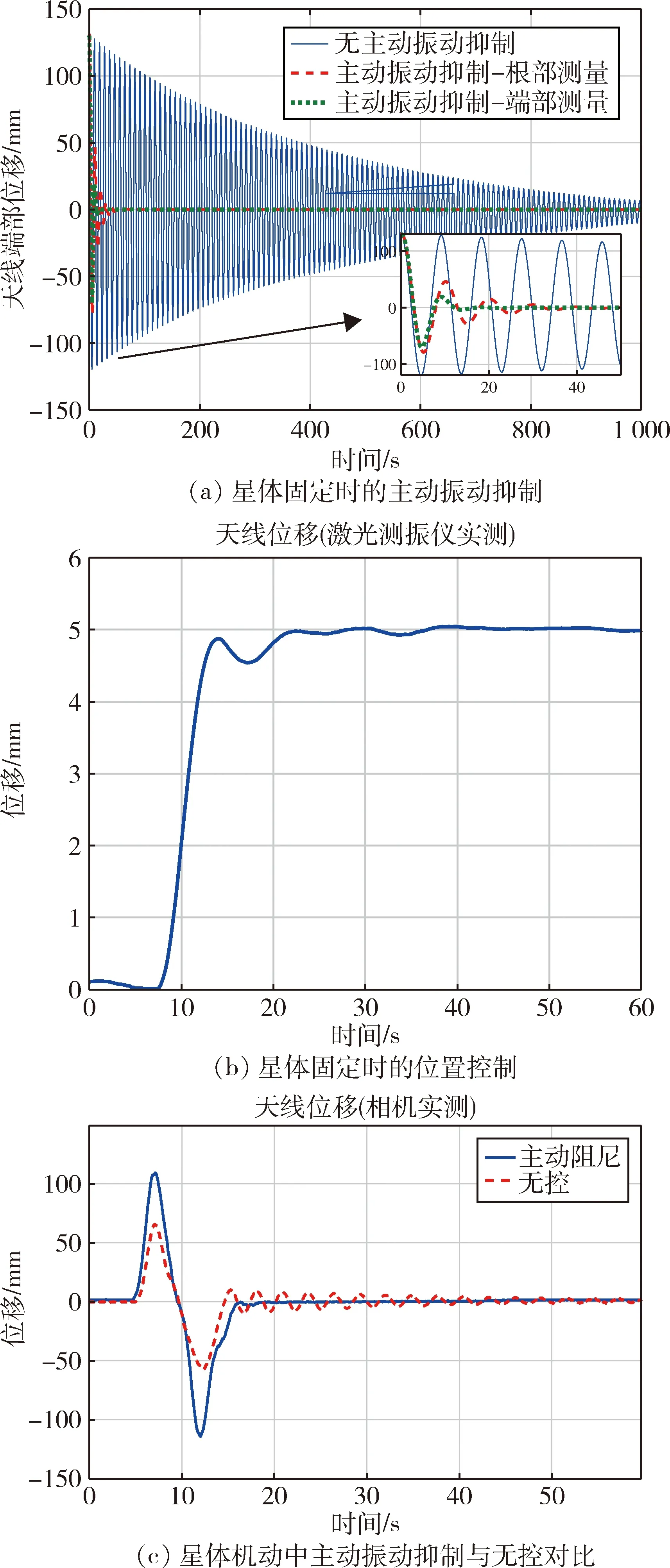
图10 主动振动抑制与位置控制试验结果Fig.10 Experimental results in active damping and position control tests

5 结 论

本文面向大型挠性天线快速主动振动抑制与高精度相对位置控制需求，提出了一种以相对位姿测量相机为传感器，以主动指向超静平台为执行机构的主动振动抑制与相对位置控制系统. 开展了动力学建模、控制器设计和数学、物理仿真试验研究. 由于传感器与执行机构非共位安装，控制律设计属于异位控制问题. 本文针对该系统提出了一种能够实现主动振动抑制与位置控制的控制器，能够为天线的一阶挠性模态提供阻尼作用，同时保持高阶模态的稳定. 控制器具有积分控制+结构滤波器的形式，也可被解释为比例-积分-微分控制器+低通滤波器. 在该控制器的基础上，设计了星体-载荷两级控制的控制器. 通过数学仿真和全物理仿真试验对控制系统在主动振动抑制和位置控制任务中的有效性进行了考核，仿真和试验结果表明，提出的控制方案和控制器能够将大型挠性天线的振动衰减时间缩短1～2个数量级，并为天线提供快速的位置调节能力.

本文中的动力学建模和控制器设计均采用了线性方法，线性方法的优势是，能够在频域刻画系统的主要特性，便于对挠性结构和控制系统的相互作用进行分析和理解. 同时，本文中采用该方法设计的控制系统也能够满足设计要求. 另一方面，先进的非线性控制方法，如自抗扰控制技术ADRC等，已应用于控制系统的设计与实践，使控制系统对不确定性和扰动具有更好的鲁棒性和适应性[21]. 在下一步工程化工作中，可以引入此类先进控制方法，以进一步提高控制性能.