一种提高多探头星敏感器姿态测量精度的方法

程会艳， 郑 然， 武延鹏， 张腾飞， 王苗苗

北京控制工程研究所,北京 100094

0 引 言

星敏感器通过对空间恒星成像来获得恒星观测矢量，采用星图匹配的方法确定星敏感器光轴在惯性空间的指向，利用星敏感器本体坐标系和卫星姿态坐标系的转换关系以确定卫星姿态[1-3].

由于可共享多个探头输出的测量数据，多探头星敏感器可以获取更高的姿态测量精度、更好的可靠性及更优的动态性能.多探头星感器数据融合的具体过程如图1所示.

图1中，首先选定一个参考探头坐标系，将其它光学探头所测量的恒星单位矢量通过探头间的相对安装矩阵转换到该视场；然后由转换后的向量联合计算卫星的三轴姿态.

图1 多探头星敏感器星图融合示意图Fig.1 Multi-FOV star sensor image fuse diagram

受空间环境等因素影响，在轨期间，产品探头间的相对安装关系会发生变化，表现为相对安装阵的变化.由于探头间安装误差变化会直接影响融合后姿态精度.因此，提高探头间安装阵估计精度是多探头星敏感器通过信息融合以实现更高姿态测量精度的核心[4-11].

探头间安装矩阵一般分为相对安装阵和绝对安装阵两部分，其估计方法可分为与姿态相关和不相关、离线处理和实时处理方法.综合比较而言，离线处理方法适用于事后处理.利用星敏输出的姿态四元数作为观测量进行探头间安装误差估计是目前常用的方法[12-20]，其中文献[13]提出了一种基于加权滤波的多头星敏感器安装矩阵校准方法，该方法通过增大临近拍权重，可得到理想的安装矩阵，但由于需要保留N拍测量信息，不能满足实时性要求.

文献[20]提出了q-AKF算法，具有较好自主性和实时性，但其利用星敏感器输出姿态数据进行安装阵估计，同时需要根据不同应用工况设计合适的衰减因子，对于安装阵估计精度提升效果有限.本文提出了一种基于星敏感器底层数据即星点数据进行在轨安装阵实时估计的方法，可提升星敏感器融合后姿态测量精度.

1 安装矩阵估计模型

首先选择产品多个探头中一个探头坐标系为基准坐标系.以探头1坐标系为基准坐标系、探头1与探头2之间安装阵估计为例进行说明.

记探头1与探头2相对安装阵在x轴、y轴、z轴变化量分别为δφ12、δφ12、δθ12，选取三轴变化量为状态变量，建立滤波器的状态方程

(1)

其中，状态变量δx=[δφ12δφ12δθ12]T，A为3阶单位矩阵，w(k)为系统模型误差，假设其为高斯白噪声.

选取星点位置矢量为观测量，建立探头1与探头2的相对安装阵估计的测量模型，如下：

zk=Hkδx+v(k)

(2)

以估计探头1与探头2相对安装阵为例，测量矩阵Hk与所选择的探头视场内星点数目有关，若选择探头1为参考探头，探头2星点数目为n颗，则观测矩阵Hk为

(3)

其中，Hk为对角矩阵，Vik为k时刻探头2视场内第i颗已识别星点对应恒星坐标矢量,i=1,2,3,…,n，hik为Vik的反对称阵.某矢量Vik=[θ1θ2θ3]，定义其反对称如下：

(4)

其中zk计算公式如下：

(5)

根据步骤(2)建立的滤波器状态方程和步骤(3)建立的测量模型，使用卡尔曼滤波算法对探头1与探头2安装阵变化量进行实时估计，具体步骤如下：

其中，I为3阶单位矩阵，T_step为滤波步长；

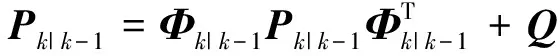
6)进行协方差阵更新

所述第1)步中，系统误差协方差阵Q在仿真中根据实际结果进行调整，R根据测量值误差进行选取，保证选择合适值使得算法稳定收敛.可采用上述同样方法对探头1与探头3间相对安装阵变化进行估计.

2 融合姿态计算方法

根据探头间安装矩阵将各探头视场内星点位置转换到基准探头坐标系下，结合选星策略选择优质星点，最后根据姿态计算方法计算融合后三轴姿态.具体实现过程如下：

1)设定其中一个探头为基准探头，该基准探头所在的坐标系为基准坐标系，一般选择原则为根据产品在轨安装布局情况，选择在轨工作温度变化相对较小的探头坐标系为基准坐标系；

2)使用上述第1节卡尔曼滤波算法对探头1与探头2安装阵变化量进行实时估计；

3)根据步骤2)得到的相对安装阵变化量，对实时安装阵进行补偿，得到修正后探头1与探头2安装阵

(6)

5)在基准探头坐标系下，选取星点位置误差较小的N颗星点，利用姿态计算方法计算得到基准探头坐标系融合后姿态数据.

3 仿真结果与分析

以某在轨应用的多探头星敏感器产品设计参数及试验数据为依据，模拟生成多轨产品数据，对上述安装阵估计算法不同工况下仿真情况进行比对分析，同时对利用该安装阵估计算法结合第2节姿态计算方法得到姿态测量精度进行仿真验证.

3.1 安装阵估计算法仿真

考虑在轨产品工作实际环境，结合其它星敏产品在轨数据分析结果，星敏探头两两间夹角存在慢变周期项，因此，仿真实验重点为对不同周期、不同幅值下的在轨安装阵误差变化估计效果进行仿真分析.同时设计仿真实验，来验证用于估计安装阵的星点数目对估计精度的影响.

(1)安装阵误差变化周期

分别对不同变化周期下产品探头间安装矩阵估计效果进行仿真，其中变化周期为6 000 s时安装阵估计效果分别如图2和3所示.

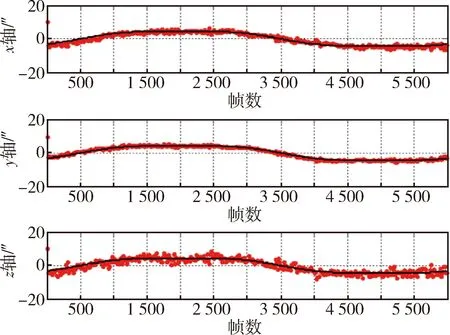
图2 安装矩阵变化周期为6 000 s时安装矩阵估计曲线Fig.2 Installation matrix estimation with 6 000 seconds period

图3 安装矩阵误差变化周期为6 000 s时三轴误差Fig.3 Star sensor errors with 6 000 seconds period

对不同周期下安装阵估计误差进行统计，得到结果曲线如图4所示.

图4 不同变化周期下三轴误差变化趋势Fig.4 Star sensor errors with different period

对上述仿真结果进行分析，结论如下：探头间相对安装矩阵变化周期越大，其对应三轴估计误差越小，在周期大于4 000 s后，其三轴估计误差基本保持不变，在轨卫星轨道周期通常为5 400 s，则产品安装阵变化趋势中显著周期项周期也在5 400 s左右.

(2)安装阵误差变化幅值

分别对探头间相对安装阵变化为不同幅值下安装矩阵估计效果进行仿真，得到幅值为5″(变化周期为5 400 s)时仿真结果如图5和6所示.

图5 安装阵误差变化幅值为5″时安装阵估计曲线Fig.5 Installation matrix estimation with 5 arc-seconds amplitude

对不同幅值下安装阵估计误差进行统计，三轴估计误差变化趋势如图7所示.

图7 不同安装阵误差幅值下三轴估计误差变化曲线Fig.7 Star sensor errors with different amplitude

对上述仿真结果进行分析，结论如下：

探头间相对安装阵变化幅值越大，其对应三轴估计误差越大，根据产品地面试验及热控设计方案，预计产品在轨两个探头间光轴夹角误差变化幅值小于3″，在该条件下，安装阵估计算法的估计误差相对较小，满足产品融合后姿态精度要求.

3)安装矩阵误差估计选用星点个数

对产品探头间安装阵变化估计时选用星数进行仿真，得到星数为5(变化周期为6 000 s)时仿真结果如图8和9所示.

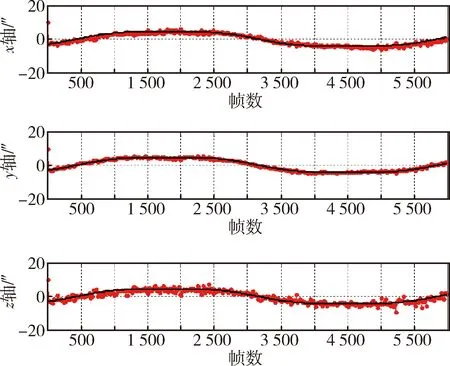
图8 星数为5时安装误差估计曲线Fig.8 Installation matrix estimation with 5 stars

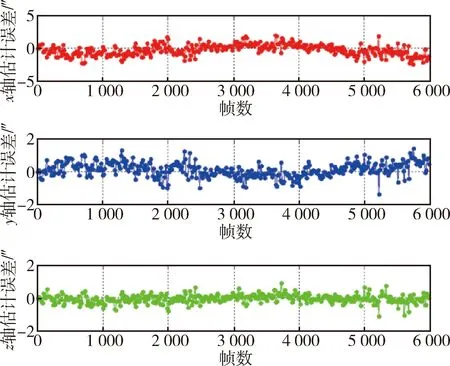
图9 星数为5时星点融合得到三轴误差Fig.9 Star sensor errors with 5 stars

对不同星数(范围从3～30，单个探头视场内平均星数在30颗左右)得到三轴估计误差变化进行仿真，得到结果如图10所示.

图10 选用不同星数三轴估计误差变化曲线Fig.10 Star sensor errors with different stars

对上述仿真结果进行分析，结论如下：

在选取星数小于10时，参与安装阵估计星数越多，对应三轴估计误差越小；在选取星数大于10颗后，其三轴估计误差改善效果不是很显著.综合考虑算法估计效果、算法计算量及处理速度，选取5颗观测星用于探头间安装阵估计.

3.2 融合姿态计算方法仿真

根据3.1节安装阵估计仿真结果选取合适参数，同时考虑产品在轨应用环境，对产品探头间安装误差变化周期为5 400 s(与在轨应用卫星轨道周期一致)、幅值为5″时，利用融合姿态计算方法得到姿态精度进行仿真验证.

由于某单位所用多探头星敏感器包含两个探头，为了与产品在轨应用条件保持一致，仿真时以两个探头为例，对两个探头融合后姿态数据精度进行分析，为了便于比对分析，同时给出了产品单个探头姿态测量精度.

由于多个探头融合后姿态精度与探头间安装夹角相关，以探头间安装夹角为60°为例，对探头间安装夹角为60°进行仿真，得到融合后姿态数据对应三轴误差，如图11所示.统计得到融合姿态数据对应三轴误差分别为x轴为0.670 4″(3σ)、y轴为0.647 6″(3σ)、z轴为0.984 2″(3σ).

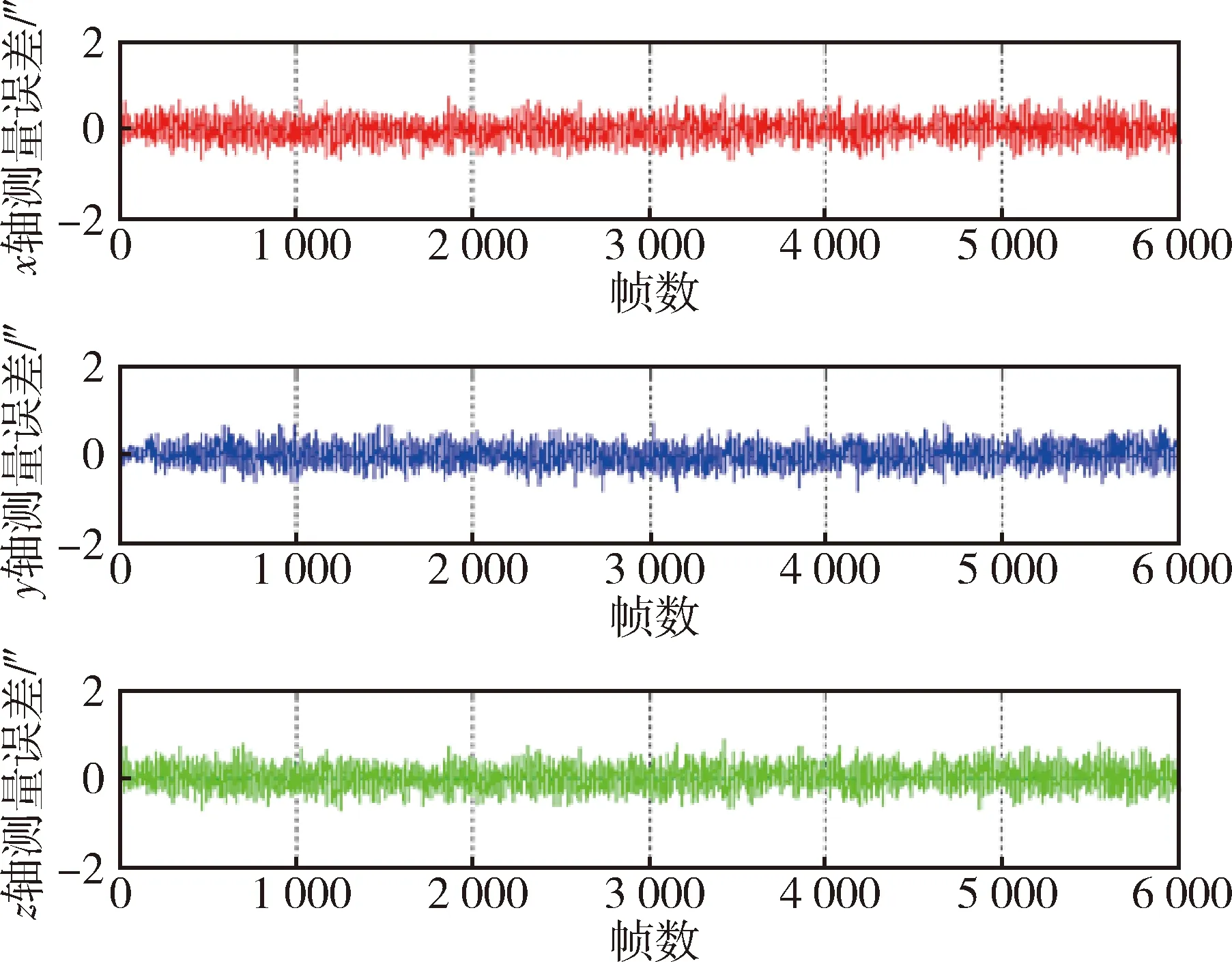
图11 融合姿态数据对应三轴误差曲线Fig.11 Star sensor errors with star fuse

利用同样精度分析方法对该时间段内单个探头姿态数据进行分析，得到单个探头对应三轴误差，如图12所示.对单个探头三轴误差进行统计，得到单个探头对应三轴误差分别为：x轴为0.935 1″(3σ)、y轴为0.960 9″(3σ)、z轴为16.565 1″(3σ).

图12 单个探头姿态数据对应三轴误差曲线Fig.12 Single star sensor errors

根据上述仿真结果可知：融合后姿态在实现了三轴同精度同时，其精度相对于单头精度提升了约30%左右.

4 在轨验证

上述安装阵估计方法已在某单位所用国产多探头星敏感器(包含两个探头)上完成了在轨验证，该卫星为太阳同步轨道，卫星角速度为0.06(°)/s.利用在轨下传的实时探头姿态数据及利用上述第2节所用融合姿态计算方法得到的融合姿态数据对产品单个探头、融合后姿态数据的姿态精度进行分析以验证提出的融合姿态计算方法对姿态测量精度的提升效果.

以在轨下传某时间段姿态数据为例，利用相邻差分法得到该时间段融合姿态数据对应三轴误差(NEA)曲线，如图13所示.

统计图13中融合姿态数据对应三轴误差(NEA)，分别为：x轴0.434 8″(3σ)、y轴0.478 9″(3σ)、z轴0.751 8″(3σ).

图13 在轨融合姿态数据对应三轴误差曲线Fig.13 Multi-FOV star fuse errors in orbit

利用相同精度分析方法得到该时间段对应单个探头三轴误差(NEA)，如图14所示.

图14 在轨单头姿态数据对应三轴误差曲线Fig.14 Single-FOV star fuse errors in orbit

统计图14中单头姿态数据对应三轴误差(NEA)，分别为：x轴0.833 5″(3σ)、y轴0.851 8″(3σ)、z轴9.796 0″(3σ).

比较图13和14对应误差统计结果可知：提出的融合姿态计算方法在实现x轴、y轴、z轴三轴同精度同时，有效提升了产品姿态测量精度.

5 结 论

对多探头星敏感器多个探头融合后姿态计算方法进行了研究，提出了一种提高多探头星敏感器姿态测量精度的方法.该方法利用星点信息作为观测量估计探头间的安装阵，有效提升了安装阵的估计精度，同时结合多视场选星策略进一步提升星敏感器的姿态测量精度.由地面仿真及在轨应用结果可知：提出的融合姿态计算方法合理有效，精度相对于单头提升了30%以上，具有一定的工程应用价值.