基于双观测器的四旋翼无人机姿态控制

姜琛 李涛,2 赵宏生

1 南京信息工程大学 自动化学院,南京,210044 2 南京信息工程大学 大气环境与装备技术协同创新中心,南京,210044

0 引言

四旋翼无人机(Quadrotor Unmanned Aerial Vehicle,QUAV)具有灵活、高效、方便等特点,在交通、建筑、防灾救援、航道巡查等领域中应用广泛[1].QUAV抗干扰能力较弱且极易受到外部环境的影响,这些都增大了其控制难度.因此,一个稳健、可靠的控制方法就显得尤为重要.现阶段,对于四旋翼无人机飞行控制系统的设计方案主要有PID控制[2]、滑模控制[3]、自抗扰控制[4]等.

目前一种有效抑制干扰的方法是基于干扰观测器的控制(Disturbance Observer Based Control,DOBC)[5].例如,针对具有已知频率的谐波干扰,可以充分利用它的已知信息,用外生系统模型来进行描述,此时DOBC可以充分发挥它在干扰的估计方面的优越性能.邵书义等[6]通过设计离散时间干扰观测器抑制外部干扰和执行器故障的不利影响,并结合干扰观测器设计离散时间控制器保证了在外部干扰和执行器故障综合作用下的四旋翼无人机系统跟踪性能;侯林林[7]将干扰观测器与L2-L∞控制相结合设计了复合抗干扰控制器,提高了非线性时变时滞关联系统的抗干扰性能.在自抗扰控制(Active Disturbance Rejection Control,ADRC)[8]中,系统内部由于建模误差等因素产生的干扰以及外部所受干扰被看作是一个“总干扰”,通过对其补偿从而提高系统的稳定性.石嘉等[9]为了提高四旋翼无人机姿态控制的抗干扰能力,设计了一种内外环嵌套结构的改进型自抗扰控制器;Lotufo等[10]提出了一种设计四旋翼无人机的完整数字姿态控制单元的原始方法,该方法是在自抗扰控制和嵌入式模型控制框架内开发的,既基于影响工厂控制的干扰和不确定性的估计,也解决了针对四旋翼无人机姿态控制过程中存在模型不确定和外界风干扰的问题.但是,他们考虑的干扰是单一的,或者将多源干扰直接合并为一个总干扰,没有充分利用不同类型干扰特性和系统性能的影响机理,保守性较大.四旋翼无人机在飞行途中会受到连续风和阵风的影响,而它们可以被视为具有已知信息的干扰和未知的非线性干扰.因此,本文分别设计干扰观测器和扩张状态观测器进行估计,然后通过基于双观测器的滑模控制律来实现对不同干扰的补偿.经过理论和仿真验证,本文设计的控制算法能够有效估计和补偿干扰并快速精确地完成姿态角的轨迹跟踪.

1 四旋翼无人机建模

四旋翼无人机是典型的欠驱动模型.假设:1)四旋翼无人机可看作理想刚体,在运动过程中不存在任何形式的形变;2)四旋翼无人机的质心与坐标原点重合;3)忽略四旋翼无人机内部存在的各种形式的摩擦和能量损耗.图1为无人机的两个坐标系,图中Fi(i=1,…,4)为每个旋翼产生的升力,ωi(i=1,…,4)为每个旋翼的转速.A系为机体坐标系,B系为地面坐标系,原点为无人机的质心.围绕X，Y和Z的欧拉角为σ=[φθφ]T,并且空间旋转分别以X,Y和Z轴的顺序变化.φ为滚转角,即围绕自身X轴旋转的角度;θ为俯仰角,即围绕自身Y轴旋转的角度;φ为偏航角,即围绕自身Z轴旋转的角度.

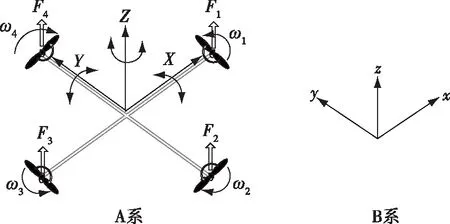
图1 四旋翼无人机系统简图

本文主要研究四旋翼无人机的姿态控制,不考虑姿态角大于90°的情况.用欧拉角来描述四旋翼无人机的空间姿态并进行建模.根据牛顿第二定律,四旋翼无人机的动力学模型[11]如下:

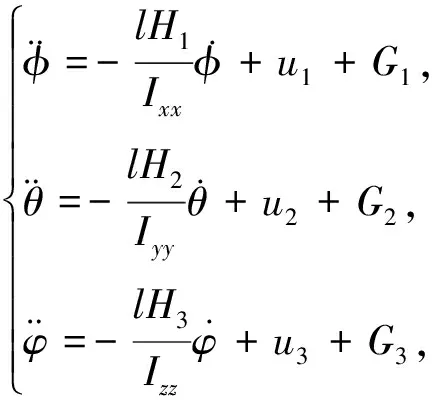
(1)

其中l表示各旋翼到机体质心的距离,Ixx,Iyy,Izz分别为四旋翼无人机机体的三轴转动惯量,Hi(i=1,2,3)为阻力系数,ui(i=1,2,3)分别为滚转角φ、俯仰角θ以及偏航角φ的控制输入，Gi(i=1,2,3)为无人机每个角所受到的干扰.这里Gi为两部分组成:

Gi=di+f.

(2)

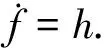
干扰di可以用如下的外生系统模型进行描述:

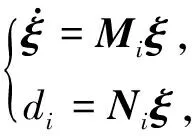
(3)

其中ξ∈R2是外生系统模型的状态向量,Mi和Ni分别为外生系统模型的系统矩阵和输出矩阵.

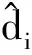
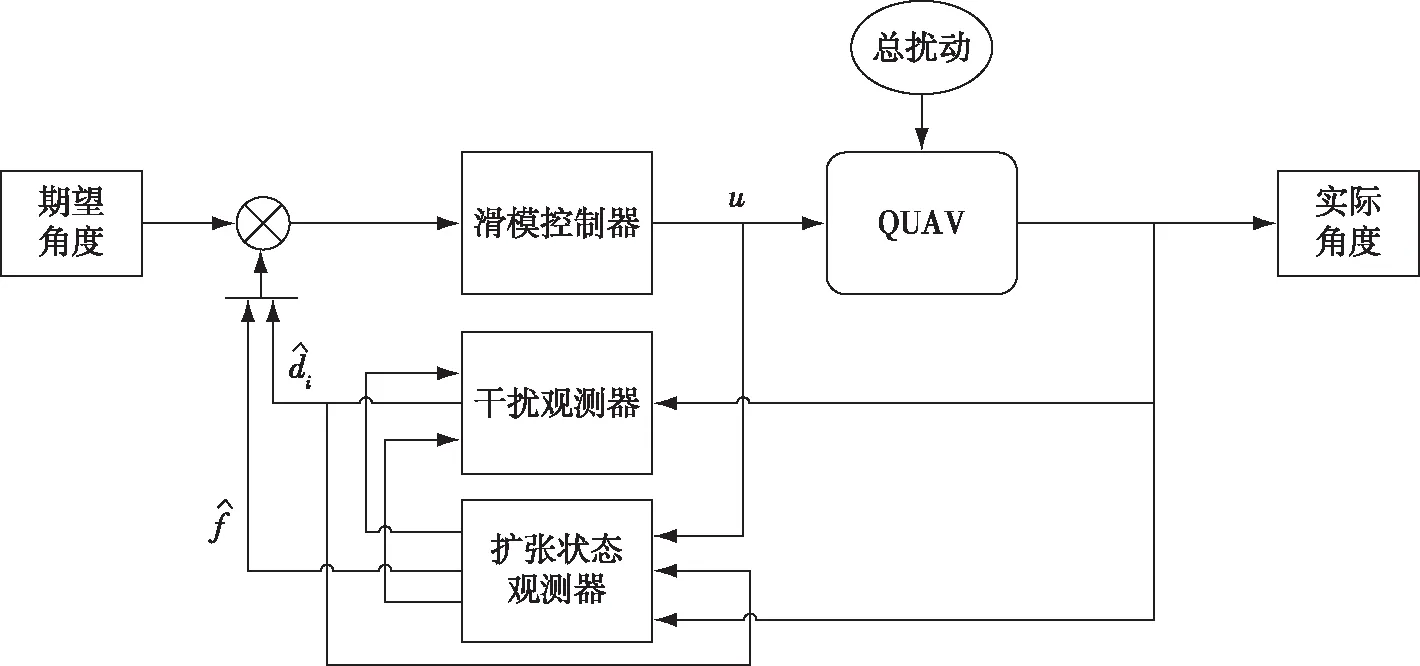
图2 四旋翼无人机姿态控制结构框图

2 双观测器设计

2.1 干扰观测器设计

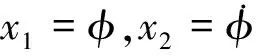
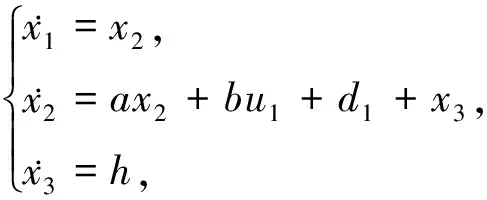
(4)

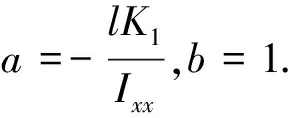
为了补偿由外生模型描述的干扰d1,设计如下干扰观测器:

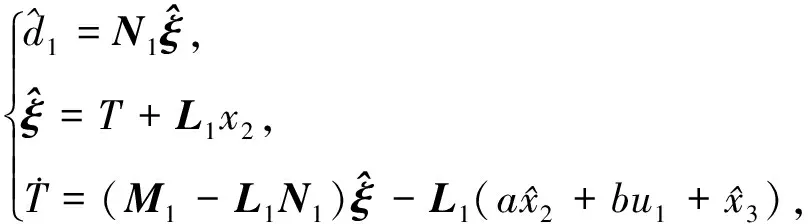
(5)

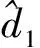
2.2 扩张状态观测器设计

此时,基于干扰观测器的输出,扩张状态观测器设计为

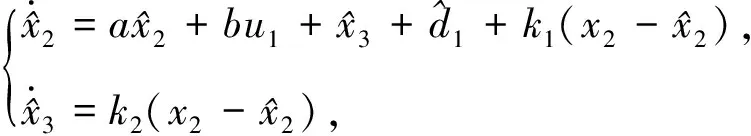
(6)

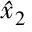
此时,根据式(3)和式(5)可以得到ξ估计误差:

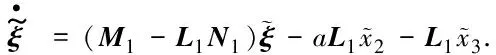
(7)

根据式(4)和式(6)得到x2和x3估计误差:

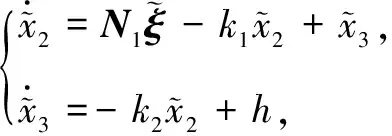
(8)

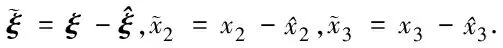
(9)

此时,干扰观测器以及扩张状态观测器的增益可以通过极点配置法进行选择.

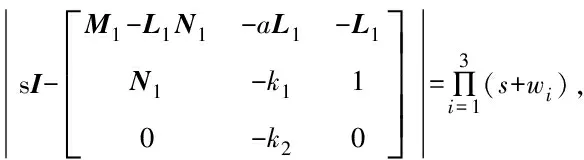
(10)

这里的wi是一个正常数.此时误差系统(9)为输入输出稳定.

注1针对误差系统(9)首先指定一组期望闭环极点λ1,λ2,λ3,并且保证所有的极点均存在负实部;然后通过格拉姆矩阵判据判定其是否能控,若系统完全能控,即满足可配置条件,再通过计算系统的多项式(10)即可求得干扰观测器以及扩张状态观测器的增益.

也可通过线性矩阵不等式(LMI)的方法求双观测器的增益,此时将估计误差系统(9)改写为

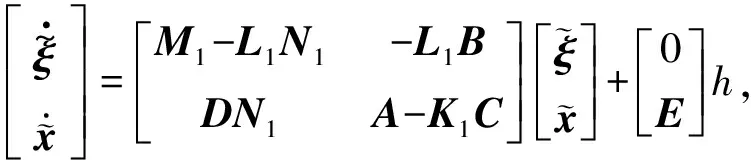
(11)

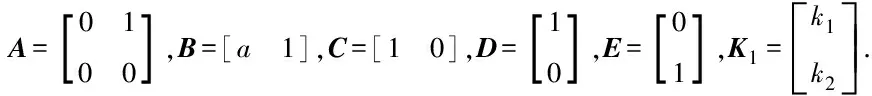
引理1[12]对于∀x,y∈Rn,存在正实数ε和正定矩阵Z∈Rn×n,满足2xΤy≤ε-1xΤZx+εyΤZy.

定理1对于系统(11),如果存在正定对称矩阵P=PΤ>0,Q=QΤ>0,常数∂>0以及矩阵Pl,Qk满足:

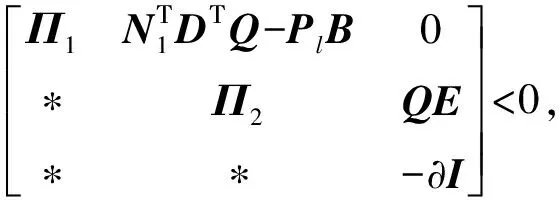
(12)

式中Π1=PM1-PlN1+(PM1-PlN1)Τ+P,Π2=QA-QkC+(QA-QkC)Τ+Q,此时通过选择观测器增益L1=P-1Pl,K1=Q-1Qk,系统(11)最终是一致有界的.

证明选取李雅普诺夫函数:

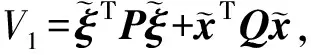
(13)

对其进行求导可得:

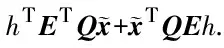
(14)

根据引理1得:

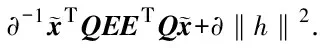
(15)

为了简单起见,定义:

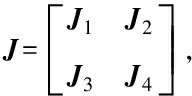
(16)

其中:

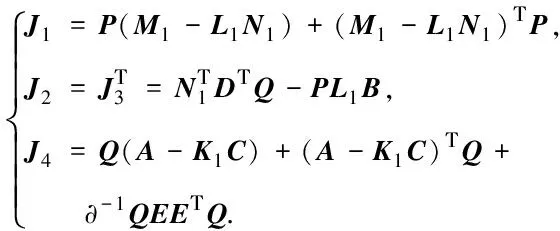
(17)

此时(15)可以简写为:

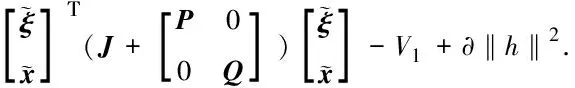
(18)

(19)

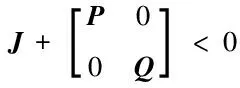
注2在本文中,具有外生模型的干扰di由干扰观测器进行估计,而可微干扰f由扩张状态观测器进行估计.与单个扩张状态观测器相比,这种处理方案充分利用对已知信息干扰的估计结果,进而提高了干扰估计的性能.

3 基于双观测器的滑模控制器设计

为了提高控制系统的响应速度以及姿态角的跟踪精度,本文采用基于双观测器的滑模控制器[13].其中φ1为给定的目标角度,φ为当前的滚转角,e为偏差且表示为

e=φ1-φ.

(20)

针对滚转角φ选取如下滑模面:

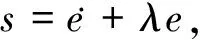
(21)

其中λ>0,并对上式滑模面求导得:

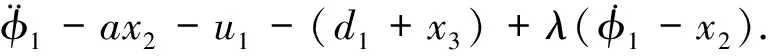
(22)

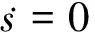
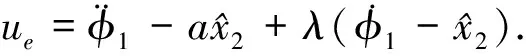
(23)

为了增强系统的鲁棒性,定义如下us:

us=ρ1s+ρ2sgn(s),

(24)

其中:

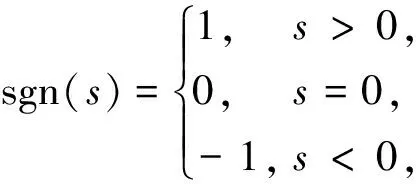
(25)

此时基于双观测器的滑模控制律为

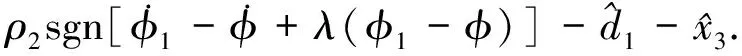
(26)

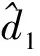
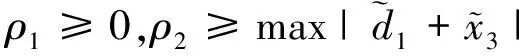
证明选取李雅普诺夫函数:

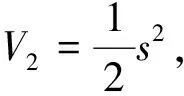
(27)

对其进行求导可得:

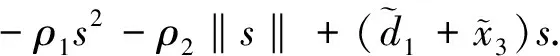
(28)

4 仿真实验分析

为了验证基于双观测器的滑模控制方案的有效性和鲁棒性,在MATLAB的Simulink环境下进行仿真.给定的四旋翼无人机动力学模型参数如下所示:m=2.5 kg,l=0.245 m,H1=0.01,Ixx=0.042 kg·m2.而干扰分为di和f.两部分干扰di表示连续风干扰,干扰f表示阵风干扰,它们分别由干扰观测器和扩张状态观测器来进行估计.首先,干扰d1=c1sin(wt+ψ1),它的已知频率w1为1,参数c1和ψ1分别被选为-1和-π/6.选取ξ1=[c1sin(wt+ψ1),c1cos(wt+ψ1)]Τ,干扰d1根据式(3)形式进行建模,其系数矩阵:

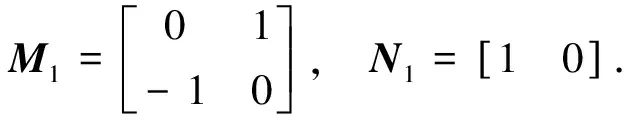
(29)

给定非线性干扰f1=-x12+2x2+0.2sin(2t),通过极点配置,干扰观测器和扩张状态观测器的增益分别为L1-1=[0.61 4.62]Τ,K1-1=[9.39 24]Τ.

干扰观测器与扩张状态观测器估计的风扰分别如图3、4所示.从图3中可以看出所设计的干扰观测器可以在4 s时准确地估计到干扰d1.同样地可以从图4中观察到扩张状态观测器对非线性干扰f1估计误差较小,观测器的性能较强.

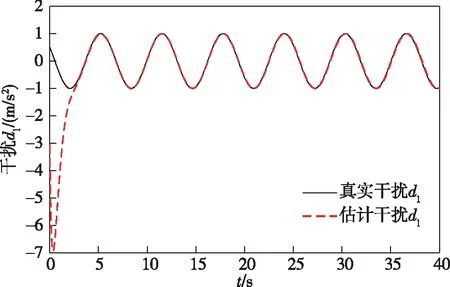
图3 干扰d1的估计

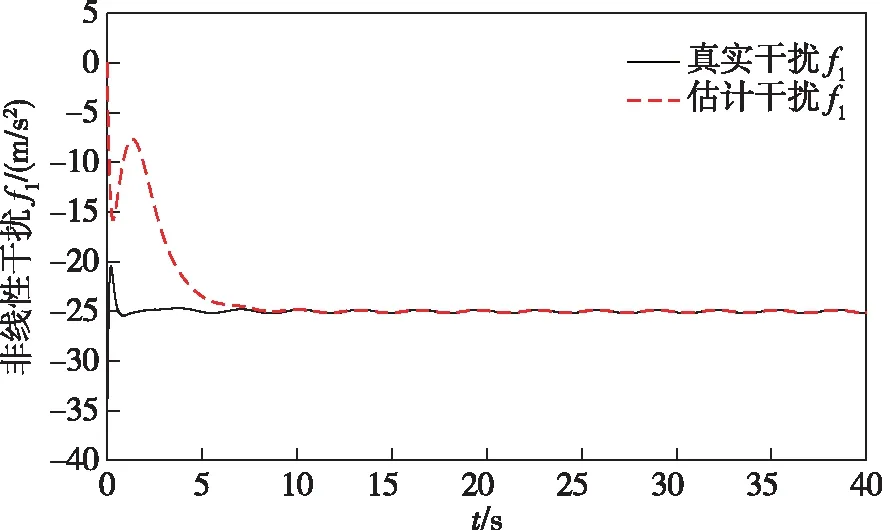
图4 非线性干扰f1的估计

对于干扰d2=c2sin(wt+ψ2),它的已知频率w2为1,参数c2和ψ2分别被选为2和0.选取ξ2=[sin(wt+ψ2),cos(wt+ψ2)]Τ,干扰d2根据式(3)进行建模,其系数矩阵:

(30)

非线性干扰给定f2=-x12+2x2+0.2sin(2t),通过LMI的方法[14]对双观测器的增益进行求解,得到干扰观测器和扩张状态观测器的增益分别为L1-2=[3.266 2.651]Τ,K1-2=[9.38 41.4]Τ.从图5和6中可以看出:相对于图3和4,此时观测器虽然可以准确估计到干扰,但是超调量较大而且所需时间更长.因此,当系统不存在不确定项时,极点配置法优于LMI的方法.

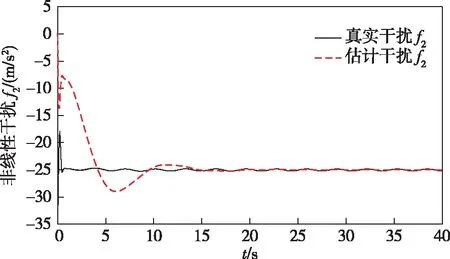
图6 非线性干扰f2的估计

滚转角、俯仰角和偏航角的跟踪仿真如图7—9所示.设定目标角度φ1=5°、θ1=6°、φ1=7°,各旋翼到机体质心的距离l为0.245 m.四旋翼无人机机体的三轴转动惯量Ixx，Iyy，Izz分别为0.042、0.051和0.09,阻力系数H1，H2，H3分别为0.01、0.05和0.1.控制器中λ=10,ρ1=20,ρ2=30.并将本文提出的控制方法与PID控制[15]进行对比，使用该文的取值,其中kp=15,ki=0.2,kd=9.可以从图7—9中清楚地看出PID控制并未能精确地跟踪到期望角度,超调量较大,而本文的控制算法超调量小,对干扰的抑制效果较好,并且对目标角度信号的跟踪精度也非常高.

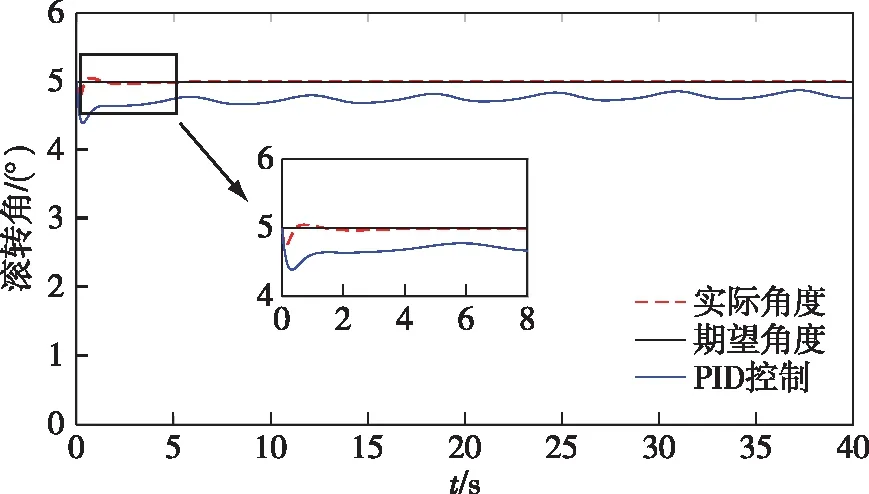
图7 滚转角φ的跟踪性能与对比

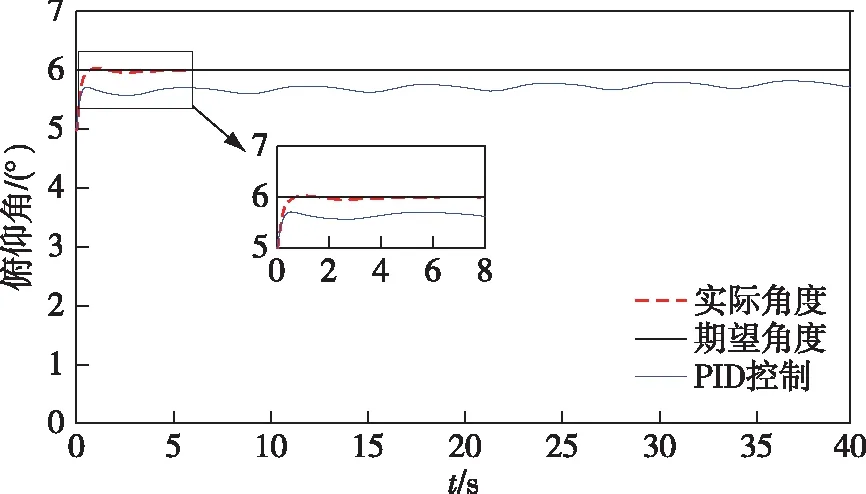
图8 俯仰角θ的跟踪性能与对比

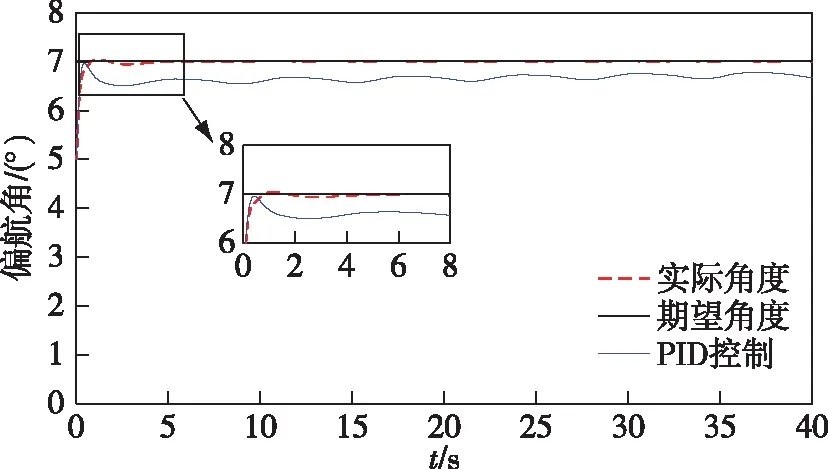
图9 偏航角φ的跟踪性能与对比

5 结束语

为了提高四旋翼无人机的控制精度和抗干扰能力,充分利用四旋翼无人机上多重干扰的特性,提出了一种新的基于双观测器的滑模控制方案.利用干扰观测器来估计外生系统模型描述的干扰,而可微干扰被扩张状态观测器估计.接着设计基于双观测器的滑模控制器,实现了四旋翼无人机的抗干扰姿态跟踪控制.最后利用李亚普诺夫理论证明了该系统的稳定性.在未来的工作中,将尝试采用实物仿真来验证所提方法的实用性.