Finite-key analysis of practical time-bin high-dimensional quantum key distribution with afterpulse effect
2022-08-31YuZhou周雨ChunZhou周淳YangWang汪洋YiFeiLu陆宜飞MuShengJiang江木生XiaoXuZhang张晓旭andWanSuBao鲍皖苏
Yu Zhou(周雨) Chun Zhou(周淳) Yang Wang(汪洋) Yi-Fei Lu(陆宜飞)Mu-Sheng Jiang(江木生) Xiao-Xu Zhang(张晓旭) and Wan-Su Bao(鲍皖苏)
1Henan Key Laboratory of Quantum Information and Cryptography,SSF IEU,Zhengzhou 450001,China
2Synergetic Innovation Center of Quantum Information and Quantum Physics,University of Science and Technology of China,Hefei 230026,China
Keywords: high-dimensional,time-bin,finite-key analysis,intensity fluctuations,afterpulse effect
1. Introduction
The unpredictable development of quantum computation undoubtedly threatens the security of classical cryptographic systems. Alternative cryptosystems must be found to safely transmit sensitive data and confidential information under serious threat of quantum computer. Quantum key distribution (QKD) is an efficient and reliable technique to resist high-performance computing attacks. It enables two legitimate parties, Alice and Bob, to share common secret key under the interference of noise and eavesdropper (Eve).[1]Basic principles of quantum mechanics including measurement-collapse theory, the Heisenberg uncertainty principle and quantum no-cloning theorem guarantee the unconditional security of QKD.[2]In recent years, the experiment of QKD has developed rapidly and made a lot of progress. The world’s first quantum satellite “Mozi” was launched in 2016[3]and a 2000-km quantum link from Beijing to Shanghai was built in 2017,[4]which initially formed a prototype of the space-ground integration quantum network.The measurement-device-independent network scheme was also proposed to connect untrusted node networks.[5]In addition, the latest experimental quantum key distribution system can reach a safe distance of 833.8 kilometers,[6]which is a breakthrough in building quantum network. However,the secret key rate of engineering prototype of QKD systems is still low. How to promote the key rate and broaden the application fields of QKD public issues requiring urgent solutions. Hardware constraints of QKD systems such as optical state generation speed, photon-counting rates and detecting dead time limit the key rate. Besides, a large fraction of photons is lost in the quantum channel due to optical absorption and scattering. Such physical and practical limitations drive researchers to seek new QKD protocols that can outperform two-dimensional protocols in both secure key rate and distance. Recent years, several high-dimensional QKD (HD-QKD) schemes has been proposed.[7–10]Photonic degrees of freedom such as position–momentum,[11]time–energy,[12]and orbital angular momentum[13,14]are proven to have a high-dimensional information loading capability,which can immensely improve the secret key rate of QKD. Generally,QKD systems using high-dimensional qudits have several superiorities than the ones using classical two-dimensional qubits. Firstly, they can effectively increase the secret key rate.n=log2(d) bits of information can be safely encoded on each single photon in HD-QKD systems.[15]Secondly,HD-QKD systems have higher resistance to quantum channel noise, which means they can tolerate a higher quantum bit error rate.[16]An attractive implementation has been proposed and its security analysis was given based on entropic uncertainty relations by Islamet al.[17]They use temporal and phase states to realize thed-dimensional protocol, in which temporal states are used to generate the key and phase states are used to guarantee the security of QKD system. The first challenge is how to prepare and measure the phase states under certain experimental resources. An equivalent protocol based on entanglement was proposed which simplifies the detector requirements for measurement.[18]Lately, another alternative scheme for four-dimensional QKD with time-bin and phase encoding was presented[19]with a simplified and compact detecting system, which presents an efficient performance than previous HD-QKD schemes and appears a broad prospects in future application.
However,the condition of its theoretical security can not be well satisfied in practical engineering conditions. Several quantum hacking attacks have been proposed by exploiting the imperfections of photoelectric devices.[22–29]Since the ideal single photon source is difficult to realize,the weak coherentstate (WCS) source is usually used in practical systems. The WCS source contains multiphoton part, which may be used by Eve through the photon-number-splitting(PNS)attack.[21]The decoy-state method[30–32]is one of means to tackle the multi-photon in WCS source. This method can estimate the counting rate and bit error of the single photon part of the WCS source, so as to estimate the secure key rate. Besides,the equipment defects of practical systems will lead to the leakage of information. The existing set-ups use the imperfect WCS source, and the intensity fluctuations[33,34]caused by intensity modulation is a nonnegligible imperfection. The avalanche photodiode single photon detectors(APD)have the nonnegligible afterpulse effect,which is created by former ignition avalanche and related to the avalanche duration time,hold-off time,lifetime of detrapping carriers. Several schemes that analyze the impact of afterpulse on QKD have also been proposed.[35–37]
Since the secret key rate in the practical protocol is limited, it is necessary to reconsider the security bound of the asymptotic region,and several methods based on finite-length key have been given.[38–40]These imperfections will lead to the correlation of detection results. Therefore, in the case of finite key and related random samples,[41]how to comprehensively take both the afterpulse and the intensity fluctuations into account in the security proof of high-dimensional schemes remains to be solved. Here,we limit the intensity fluctuations of the sources to a certain range by setting the intensity fluctuations parameters. We also introduce the afterpulse probabilities into the formula of secret key rate with different dimensions. Considering finite-length effects,we apply Azuma’s inequality to tackle the statistical fluctuations of relevant random samples in the security bound.[42]
In this paper, we give the implementation process of the four-dimensional time-bin protocol and extend it to the eightdimensional protocol in Section 2. Then we analyze the impact of the afterpulse effect and the intensity fluctuations on the secret key rate in practical protocols in Section 3. In addition,the simulations of key rates for the different afterpulse effect and intensity fluctuations in two schemes are provided in Section 4.
2. Protocol description
Firstly, we introduce the four-dimensional scheme based on time-phase states. The eight states of four-dimensional(4D) scheme and the experimental setup have been given in Ref.[19]. Time-bin qudits can be easily created by weak coherent pulses. Pulses in different time slots form the different bases and the superposition among these pulses is devised by controlling the relative phase of the pulses. The analysis of one-decoy protocol has been given and it has been proved that the one-decoy protocol has better performance in the practical protocol.[20]Let the choesn probabilities ofZandXbases arepZandpXrespectively. The secret key is extracted only when two parties both selectZbasis,while the information leakage is estimated from the events when two parties both selectXbasis. The specific protocol process is shown below.(iii)Basis reconciliation

Fig.1. Experimental setup for measurement.[19] PC:polarization controller;BS:beam splitter;PBS:polarizing beam splitter. After the qudit is polarized,it interfered at BS2. The delay (τ or 2τ) of the interference depends on the polarization. The specific interference results are shown in Fig.2.

Fig.2. τ is the time-bin duration. Alice and Bob both select Z basis and here is the interference of the four states respectively. We can distinguish the four states by the response of detectors and the arrival time. For example,the SPAD 1 responds in the second time slot,we believe that the state received by Bob at this time is|t1〉.
Alice and Bob announce their bases and intensity choices over an authenticated public channel. Then they record the number of the detected pulses underkintensity when they choose the same basis, wherenZ,kandnX,kcorrespond to theZbasis and theXbasis,respectively.[41]
(iv)Parameter estimation
Alice and Bob calculate the bit errorsmX,kfor intensitykwhen they both choose theXbasis. Then they calculate the lower bound of single-photon eventssZ,1,sX,1, the lower bound of vacuum photon eventssZ,0and the upper bound of the errorscZ,1for the single-photon events in theZbasis.If the phase error rateφ=cZ,1/sZ,1is lower than the predetermined phase error rate ¯φ, Alice and Bob accept the the raw key and perform post-processing,or they abandon the protocol.
(v)Postprocessing
Alice and Bob carry out the error correction,which consumes at most LeakECbits.Then they carry out the error verification and privacy amplification to obtain the secret key lengthℓ.
The protocol can be extended to higher level. We realize the protocol expansion from four-dimension to eightdimension without adding detectors and other devices and here are the eight qudits ofZbasis(see Fig.3). In the preparation,we expand two photonic wave packets within a frame of four contiguous time bins to four photonic wave packets within a frame of eight contiguous time bins, and two sets of random numbers are required to edit the phases of adjacent photonic wave packets. In order to ensure that the eight qudits are perfectly orthogonal, we assume that the ratio of time-bin duration to pulse width is greater than 7.7[43]and we neglect the problem of time jitter in this situation. Also,the time-bin duration should be adjusted to ensure that the dead time of the SPADs is shorter than the time slot between two peaks.[44]realizes the minimum dead time of avalanche photodiode of 12.4 ns, so we can set the minimum dead time as the duration between two peaks ideally. Therefore, the minimum duration of each qudit can reach approximately 24.8 ns. Here,we have analyzed the scheme that the qudit have 6 or 7 time bins. When there are 6 or 7 time bins per qudit,it is possible for the eight states belonging to any basis orthogonal to each other. However, it cannot satisfy the condition that the two bases are mutually unbiased. Therefore,we coding the qudits in eight contiguous time bins.

Fig.3. The eight states of Z basis belonging to the eight-dimensional(8D)protocol,0 and π specify the relative phase between the different time bins occupied by the photon. When two SPADs response twice in total,we can distinguish the current state according to the response of the two detectors and the arrival time of clicks. The specific process is similar to the fourdimensional protocol.

Table 1. The method of distinguishing eight signal states in measurement.
In the measurement,we distinguish the eight states by the response of the two detectors and arrival time of the clicks(see Table 1).
3. Security analyses
The security analysis is based on the composable security definition,we say our protocol isε-secure meansεsec+εcor≤ε, whereεcoris the correctness parameter andεsecis the secrecy parameter.[45]The length of secret key per privacy amplification block in theZbasis can be given by[17]

The error rate of then-photon states and the overall quantum bit error rate(QBER)is given by[46]

whereedis the baseline system error rate,e0is the error rate of the background. We assume thee0of four-dimensional scheme to be random ande0=3/4.
Then we consider the afterpulse effect. Considering the dead time of SPADs,not all afterpulse can be detected. Based on the previous work,[35]we propose another method to calculate the afterpulse probability. Letpirepresent the probability that the nexti-th gate triggers an avalanche after an avalanche trigger. Here,we no longer consider the high-order afterpulse,but directly counting the probability of generating clicks in a period of time after a trigger. Then,we can obtain the overall probability of the afterpulse

Next,combined with the obtained the overall probability of the afterpulse,we can characterize the count rateQµand the overall QBEREµ. Here, we assume that the triggers caused by the background count also cause the afterpulse, and it can be expressed as follows:

In practical time-bin HD-QKD system, the imperfections of practical devices should be considered. The laser sources and the intensity modulators will bring the intensity fluctuations.[47,48]In this work, we take the intensity fluctuationsk ∈{µ1,µ2,µ3}into account. Assuming that the intensity fluctuations of source is within a certain range and we can


4. Simulation
In this section,the QKD schemes are tested over different channel lengths of standard single-mode fiber. In simulation,we traverse theZbasis selection probabilities, the emission proportions of signal light and the intensities of signal(decoy)light to obtain a optimal secret key rate. The values of parameters are listed in Table 2.

Table 2. The parameters values of simulation. N is the total number of pulses, fe is the error-correction efficiency,εsec and εcor are the security parameters,Y0 is the background counting rate, ed is the misalignment-error probability.
For the case with the intensity fluctuations,we simulated the effect of the different intensity fluctuation parametersδon the secure key rate of one-decoy protocol. The generation of key rate decreases evidently with the intensification of source intensity fluctuations. The secure key rate decreases sharply when the parameter exceeds 20%, and almost no key is generated when the parameterδexceeds 25%. In practical QKD system, the afterpulse of detectors also affects the secure key rate. The afterpulse effect will lead to bit error, and each detected afterpulse in the 4D protocol will bring 75%error bit.The increase of afterpulse probability and transmission distance will directly lead to the increase of overall QBER in Eq. (10). And the longer the transmission distance, the more sensitive the QBER is to the afterpulse probability. Therefore,the afterpulse indirectly raise the upper bound of the phase error rateφUZin Eq.(1). Figure 4 shows the curve of secure key rate with the different afterpulse probability. As shown in the figure that the maximum transmission distance decreases with the increase of the afterpulse probability. When the afterpulse probability reaches 3%,the key rate decreases rapidly,and the intense afterpulse of detectors will lead to a sharp reduction in key rate.
According to Fig. 5, the line represents the 4D scheme and the dotted line represents the 8D scheme,we provide the key rate curves of the two schemes under different parameters.The eight-dimensional scheme generates more secure keys under normal attenuation, the key rate of 8D scheme is at least 1.5 times higher than that of 4D scheme. However,in the case of extreme attenuation,the performance of 8D scheme is gradually inferior to that of 4D scheme. When we consider the two parameters on the key rate,it will aggravate the decline of the key rate. As shown in Fig.4,when only the afterpulse effect is considered in the 4D scheme,there will be a significant attenuation of the transmission distance whenpap=3%. However,when the intensity fluctuations is considered at the same time,the tolerance for the afterpulse effect is greatly weakened and the sharp reduction occurs whenpap=2%.

Fig. 4. Optimal secure key rate (per pulse) of one-decoy approach for different values of the afterpulse probability with no intensity fluctuations.The key rate and the longest transmission distance decrease sharply after the afterpulse probability exceeds 2.5%.

Fig. 5. The solid line represents the 4D scheme and the dotted line represents the eight-dimensional scheme,we provide the changes of the key rate curves of the two schemes under the strength fluctuations parameter δ=0%,15%and the afterpulse probability pap=0%,1.3%,2%.
In addition, we compare the effects of the intensity fluctuations and the afterpulse effect to schemes in different dimensions. We propose the ratiosθintandθpapto characterize them, whereθintis the ratio before and after considering the strength fluctuations andθpapis the ratio before and after considering the afterpulse effect(see Fig.6). As can be seen from the figure,the key rate reduction of the 8D scheme before and after considering the strength fluctuations is obviously better than that of the 4D scheme,while 4D scheme performs better only considering the afterpulse effect. This is because the 8D scheme’s error rate of the backgrounde0is greater than the 4D ones. From Eq.(10),we know that the 8D scheme has greater overall QBER considering the afterpulse. The stronger the afterpulse effect,the greater the overall QBER,which increases the estimation of phase error rateφUZ. Therefore,the tolerance of 8D scheme to afterpulse effect is not as good as that of 4D scheme. In conclusion,the 8D protocol has stronger tolerance to the intensity fluctuations,but is more sensitive to the afterpulse.
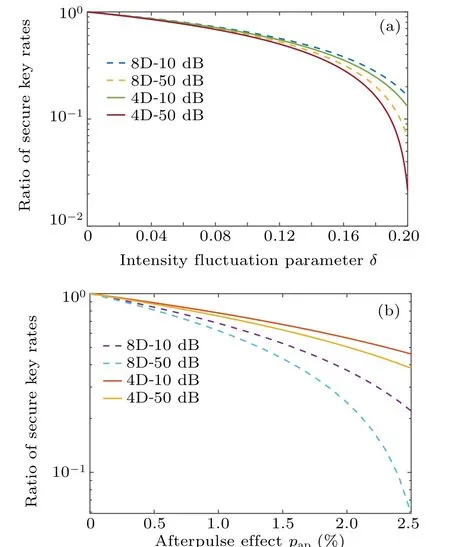
Fig.6. The two ratios to characterize the effects of the intensity fluctuations and afterpulse. (a)Efficiency of the intensity fluctuations θint, and δ is the fluctuations parameter. (b) Efficiency of the afterpulse θpap, and pap is the overall probability of the afterpulse.
5. Conclusion
For the practical HD-QKD, the flaws of source and detector restrict the key rate of practical high-dimensional protocols. In this paper, we extended the 4D time-bin protocol,and the effect of the intensity fluctuations and afterpulse have been mainly considered. We utilized parameters to limit the intensity and applied Azuma’s inequality to establish the relationship between the expected and practical value. Besides,the afterpulse probability is introduced to quantify its effect to the generation of secure key rate. In numerical simulation,we simulated the effect of two flaws to schemes with different dimensions. It is found that both two flaws will reduce the key rate, but the 8D scheme is more sensitive to the afterpulse and has better robustness than the 4D scheme. Form the simulation, our results emphasized the significance of the stable source and high-performance detector in practical HDQKD. In conclusion, we derived an analytical model to the variant practical time-bin QKD protocol considering the intensity fluctuations and the afterpulse effect.It provides a theoretical reference for secure analysis of practical high-dimensional protocols.
Acknowledgements
Project supported by the National Key Research and Development Program of China(Grant No.2020YFA0309702),the National Natural Science Foundation of China (Grant Nos. 62101597, 61605248, 61675235, and 61505261),the China Postdoctoral Science Foundation (Grant No. 2021M691536), the Natural Science Foundation of Henan Province, China (Grant Nos. 202300410534 and 202300410532), and the Anhui Initiative Fund in Quantum Information Technologies.
猜你喜欢
杂志排行
Chinese Physics B的其它文章
- Magnetic properties of oxides and silicon single crystals
- Non-universal Fermi polaron in quasi two-dimensional quantum gases
- Purification in entanglement distribution with deep quantum neural network
- New insight into the mechanism of DNA polymerase I revealed by single-molecule FRET studies of Klenow fragment
- A 4×4 metal-semiconductor-metal rectangular deep-ultraviolet detector array of Ga2O3 photoconductor with high photo response
- Wake-up effect in Hf0.4Zr0.6O2 ferroelectric thin-film capacitors under a cycling electric field
