基于神经网络的双闭环伺服系统自适应控制*

刘 洋， 赵凯岐

(哈尔滨工程大学 智能科学与工程学院，黑龙江 哈尔滨 150000)

0 引 言

永磁同步电机(PMSM)以其损耗小、功率密度大、效率高等优点[1]，已经在电动舵机、机器人以及无人机等伺服系统中得到广泛应用。然而高端应用场合也对其控制性能提出了更高的要求[2]。由于PMSM伺服系统自身是一个多变量、强耦合的非线性系统[3]，必须克服外界随机干扰和自身非线性的影响才能实现其高性能控制。因此由PMSM构成的伺服系统的控制技术成为研究热点[4]。

为了提高伺服系统的抗扰和补偿能力，韩京清[5]提出了一种新型控制方法——自抗扰控制(ADRC)。ADRC的核心是扩张观测器(ESO)，思想是将串联积分器的形式作为被控对象的规范形式，将与上述形式不同的扰动看作总扰动，并加以估计和补偿。自ADRC出现以来,不断有学者尝试将其应用于PMSM的控制中[6]。文献[7]已经成功将ADRC应用在船舶永磁电机控制系统，提高了系统的抗干扰能力和鲁棒性；文献[8]借鉴滑模控制的思想，实现了位置环采用ADRC的PMSM伺服系统一体化设计。然而，对于复杂工况下的伺服系统，一组固定参数的ADRC很难达到最优控制效果[9]，因此参数整定的问题限制了其推广与应用。神经网络是近几十年来迅速发展的前沿课题，相关研究人员不断将神经网络等智能算法引入ADRC系统，实现其参数的整定与优化，并取得了丰硕的成果。文献[10]将小波神经网络与ADRC相结合，实现ADRC参数自整定，但是小波神经网络收敛速度较慢，容易造成伺服系统中转子位置跟踪效果较差，限制了系统的性能；文献[11]将性能优异的径向基函数神经网络(RBFNN)和交流伺服系统相结合，但仅仅是对PID参数进行在线整定，而ADRC核心ESO的参数还是采取传统的试凑法，降低了系统的自适应能力；文献[12]利用模糊布谷鸟算法实现变桨距ADRC的参数自整定，虽然该改进算法避免陷入局部最优解，但是该方法遗传算子的选择比较复杂，因而必须要经过相应改进才可能满足高性能要求。

本文基于ADRC控制的PMSM位置伺服系统采用位置-电流双闭环控制。综合考虑上述优化算法的各种优劣，采用学习速度较快、可以满足实时性要求的径向基函数神经网络(RBFNN)在线整定ADRC的部分参数，设计线性状态误差反馈(LSEF)进一步降低参数整定复杂性，简化了伺服系统的控制结构。并通过与传统ADRC的伺服系统进行位置跟踪精度、动态响应能力以及稳态性能对比分析。仿真结果表明：该控制策略在保持伺服系统良好稳定性的同时，降低了ADRC参数调参的复杂程度，提高了控制器对位置的跟踪速度，增强了系统的抗扰能力、补偿能力以及鲁棒性。

1 PMSM数学模型及扰动分析

PMSM在d-q旋转坐标系下的数学模型如下。

电磁转矩方程为

Te=p[ψfiq+(Ld-Lq)idiq]

(1)

式中：id、iq分别为d-q坐标系下的电流分量；Ld、Lq分别为d-q坐标系下的电感分量，取Ld=Lq；ψf为磁链参数；p为极对数。

机械运动方程为

(2)

式中：ωr为机械角速度；J为转动惯量；B为阻尼系数；TL为负载转矩。

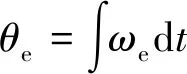
(3)

式中：θe为转子位置角；ωe为电角速度。

在位置-电流双闭环伺服系统中，电流内环的响应更快，外环的响应较慢。为了满足伺服系统实时性的要求，采用id=0的控制方式，电流环采用PI控制，位置环则采用二阶ADRC，用于优化转子位置跟踪效果，这样不仅保证了电流的响应速度，也降低了计算的复杂性。由式(1)与式(3)得PMSM二阶运动方程：

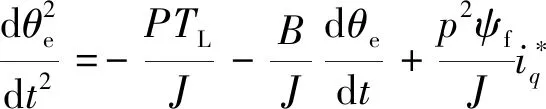
(4)

将式(4)整理为标准化被控对象位置环状态方程：

(5)

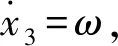
(6)

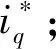
2 ADRC技术

ADRC是处理动态不稳定、内外干扰同时存在、非线性等问题的一种有效工具[13]。其主要由三部分组成：跟踪微分器(TD)、ESO、非线性状态误差反馈(NLSEF)[14]。二阶ADRC结构图如图1所示。给定目标速度v，由TD经过渡过程得到实际模型跟踪的速度v1和速度微分v2。ESO根据PMSM的控制输入和实际输出得到观测的速度z1、速度微分z2和扰动z3，与跟踪速度v1和速度微分v2作差得到速度误差e1和速度微分误差e2。由NLSEF将误差进行非线性组合，减去总扰动即为实际的控制量，进而控制PMSM。

2.1 TD

TD用来为输入信号安排过渡过程，进而使得到的输出信号更加光滑，满足了伺服系统的快速性并且减小伺服系统位置跟踪过程中的超调量。选择最速综合控制函数fhan(v1,v2,r,h)构成TD。

二阶跟踪微分器表达式为

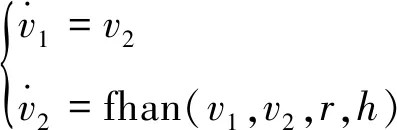
(7)

fhan(v1,v2,r,h)可以定义为

式中：v0为输入信号；v1为TD提取的输入信号v0的过渡过程；v2为v1的微分状态信号；r为速度因子；h为控制器步长；d、d0、a0、a、y均为中间变量。

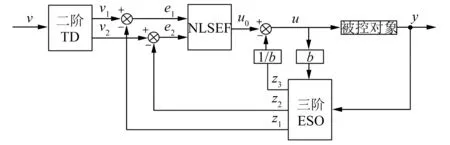
图1 二阶ADRC结构图

2.2 ESO

ESO作为ADRC的核心部分，用来实时估测系统中的不明确扰动，并将影响被控对象的扰动扩张作为新的状态变量。

三阶扩张观测器表达式为

(8)

Fal(e,α,δ)的函数表达式为

(9)

式中：α1、α2为非线性因子；β01、β02、β03为非线性误差增益；δ为滤波因子；b为补偿因子；z1、z2为y的跟踪信号；z3为扰动估计值。

2.3 NLSEF

NLSEF用以计算ESO的跟踪信号与TD输出信号间的误差，并将误差进一步组合得到系统的控制量。

NLSEF表达式为

(10)

式中：α3、α4为非线性因子；β1、β2为误差增益；δ1、δ2为滤波因子；e1为给定信号误差；e2为输出信号误差；u0为待补偿控制指令。

在NLSEF中需要整定的参数有非线性误差增益β1、β2，非线性因子α3、α4，滤波因子δ1、δ2,需要整定的参数较多。针对这一问题，文献[15]设计了一阶线性自抗扰控制器(LADRC)系统，降低了参数整定的复杂性，提高了系统的性能。文献[16]对引入LSEF的问题进行了分析，并成功将线性/非线性ESO和LSEF结合。受文献[16]的启发，针对二阶ADRC，本文设计LSEF取代NLSEF，保留了ESO不需要控制对象精确数学模型的优点，同时减少了待整定参数，提高了控制系统的性能。

LSEF表达式为

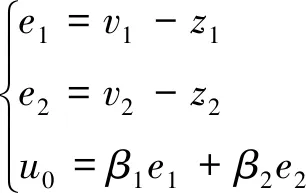
(11)

扰动估计补偿表达式为

(12)

式中：u为补偿控制指令。

3 基于RBFNN的ADRC控制器

为提高ADRC的自适应能力，采用神经网络在线整定其部分参数。通过仿真运行m文件调用Simulink结果，再用随机遍历获得的训练样本点。然后神经网络进行离散训练，将网络权值设置在合理范围，最后根据仿真波形情况在线微调，用以获得最优控制信号。

3.1 RBFNN原理

RBFNN是由输入层、隐藏层和输出层组成的三层前馈式网络。图2所示为n-m-1的RBFNN拓扑结构图。

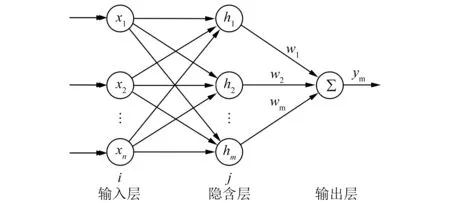
图2 RBFNN拓扑结构图

图2中，通过非线性映射将输入层的数据映射到隐含层，过程中需要一个局部逼近、非负非线性以及径向对称的径向基函数。因此，隐含层激励函数选取性能优良的高斯函数，具体表达式为

(13)

式中：ci为网络第i个隐含层的中心点,ci=[ci1,ci2,…,cin]T；bi为第i个隐含层节点的基宽度参数；m为隐含层节点数。

RBFNN的隐含层到输出层变换是线性映射，即神经网络的输出ym可表示为

ym=w1h1+w2h2+…+wmhm

(14)

式中：w1、w2、…、wm为RBFNN的权向量。

RBFNN的目标性能输出函数为

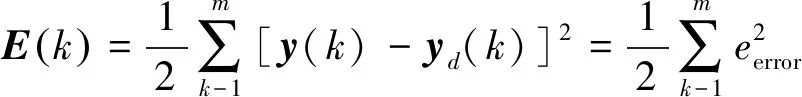
(15)

式中：y(k)为网络实际输出；yd(k)为网络预期输出。

通过梯度下降法确定RBFNN的输出层权值wi(k)、节点宽度bi(k)及中心ci(k)，其迭代算法如下：

(16)

式中:η为学习速率；α为动量因子。

3.2 RBFNN-ADRC位置调节器设计

ADRC控制量的生成依赖于ESO对总扰动的观测和估计，为了使在线整定的参数能够更好地适应系统宽范围、实时性的控制要求，文献[17]提出了一种增量式PI控制算法实现PI参数的在线整定。本文RBFNN的输入信号选择为信号误差e1、信号微分误差e2以及观测误差eerror，输出信号为β01、β02、β03。图3为RBFNN-ADRC位置调节器框图。

结合系统输入与输出间的误差，定义ESO中β01、β02、β03三参数的增量系数如下：

(17)

RBFNN的误差为

eerror(k)=y(k)-yd(k)

(18)

定义ESO中三参数整定式如下：

(19)

RBFNN的Jacobian矩阵算法为

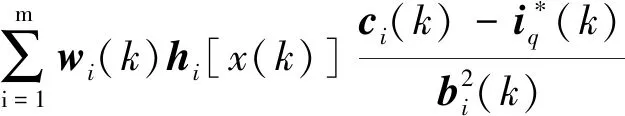
(20)

图3 基于RBFNN优化的ADRC位置调节器结构图

基于RBFNN在线整定ESO参数的训练过程大体可概括为

(1) 确定神经网络的结构，选定学习速率η=0.1和动量因子α=0.05；

(2) 采样得到y(k)和yd(k)，计算此时刻的误差eerror(k)和Jacobian矩阵；

(3) 计算神经网络输入层和输出层；

(4) 验证上一步取值是否满足性能指标，若满足则直接进入(6)，否则执行下一步；

(5) 执行神经网络迭代学习，令k=k+1，返回到(2)；

(6) 将满足性能指标的β01、β02、β03输入ESO观测器。

4 仿真结果及分析

为验证基于RBFNN-ADRC伺服系统的位置跟踪性能，根据图4所示的框图，在Simulink中搭建仿真模型，对PMSM基于传统ADRC和基于RBFNN-ADRC进行仿真分析对比。表1和表2为仿真过程中PMSM模型参数和ADRC参数的设定情况。

图4 基于RBFNN-ADRC的PMSM伺服系统控制图

表1 电机仿真模型参数

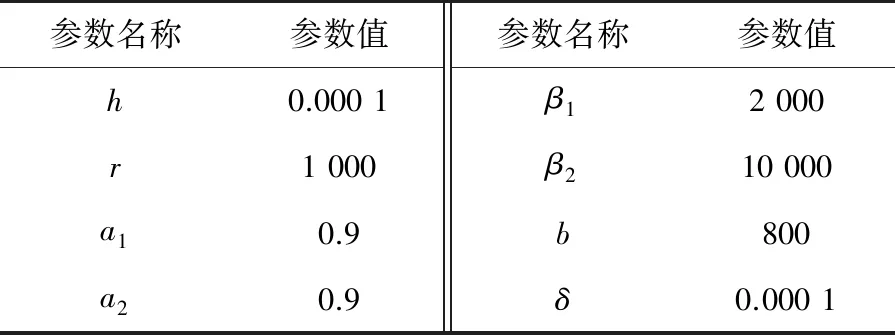
表2 ADRC参数

在实际工作过程中，PMSM的转子位置时刻均在变化，为使实际转子位置在不同工作状态下均能够无超调并且快速地跟踪目标转子位置，本文分别采用具有代表性的阶跃输入信号、正弦输入信号以及方波输入信号作为转子位置给定信号，目的是为了更直观地验证基于ADRC的系统和基于RBFNN-ADRC的系统之间的性能差别。其中阶跃输入信号的期望幅值为2°，正弦和方波输入信号的期望幅值为1°，频率为2.5 Hz，仿真时间为0.5 s。电机空载起动，在0.3 s时突加2 N·m的负载，以此验证基于RBFNN-ADRC的系统转子位置跟踪效果。仿真结果如图5～图10所示。

图5 阶跃输入转子位置跟踪曲线

图6 阶跃输入转子位置跟踪误差曲线

图5和图6为伺服系统在阶跃输入条件下的转子位置跟踪曲线和跟踪误差曲线。比较图5中基于传统ADRC和基于RBFNN-ADRC的系统仿真波形，二者均无超调。基于传统ADRC的系统达到目标期望值的时间为0.12 s，其响应曲线的稳态误差值为0.000 2°，突加负载后转子实际位置为1.969°，跟踪误差达到了0.031°；基于RBFNN-ADRC的系统仿真波形在0.044 64 s时就完全跟踪目标期望值，稳态误差几乎可以忽略不记，突加负载后其转子实际位置为1.998°，跟踪误差为0.000 2°，其动态品质和稳态性能比传统ADRC更优异。

图7和图8为伺服系统在正弦输入条件下的转子位置跟踪曲线和转子位置跟踪误差曲线。与阶跃输入信号一样，在正弦输入信号条件下，图7中基于传统ADRC的系统转子位置具有较大的跟踪误差，在0.103 s幅值才仅达到0.998 8°，在0.201 s时其跟踪误差高达0.103°。而基于RBFNN-ADRC的系统在0.102 s就达到期望幅值1°，最大跟踪误差仅为0.047 8°。在0.3 s突加2 N·m负载后，基于传统ADRC的系统在0.304 7 s时，转子跟踪波形跌落至-1.01°，恢复稳定用时0.022 s。而基于RBFNN-ADRC的系统最大跌落值为-1.006°，且用时0.001 s就恢复至稳定状态。由此说明基于RBFNN-ADRC的系统比传统ADRC控制方式表现出更快的响应速度和更小的稳态误差。

图7 正弦输入转子位置跟踪曲线

图8 正弦输入转子位置跟踪误差曲线

图9和图10为伺服系统在方波输入条件下的转子位置曲线和转子位置误差曲线。由图9可以看出，在输入信号为方波信号的条件下，与基于RBFNN-ADRC的系统相比，基于传统ADRC的系统达到稳定跟踪目标位置所用时间更长，稳态误差更大，在0.3 s突加2 N·m负载后，转子位置跟踪精度误差也较大。通过转子位置跟踪仿真表明，与基于RBFNN-ADRC的系统相比，基于传统ADRC的系统动态性能、稳态性能以及抗扰能力均更差。

图9 方波输入转子位置跟踪曲线

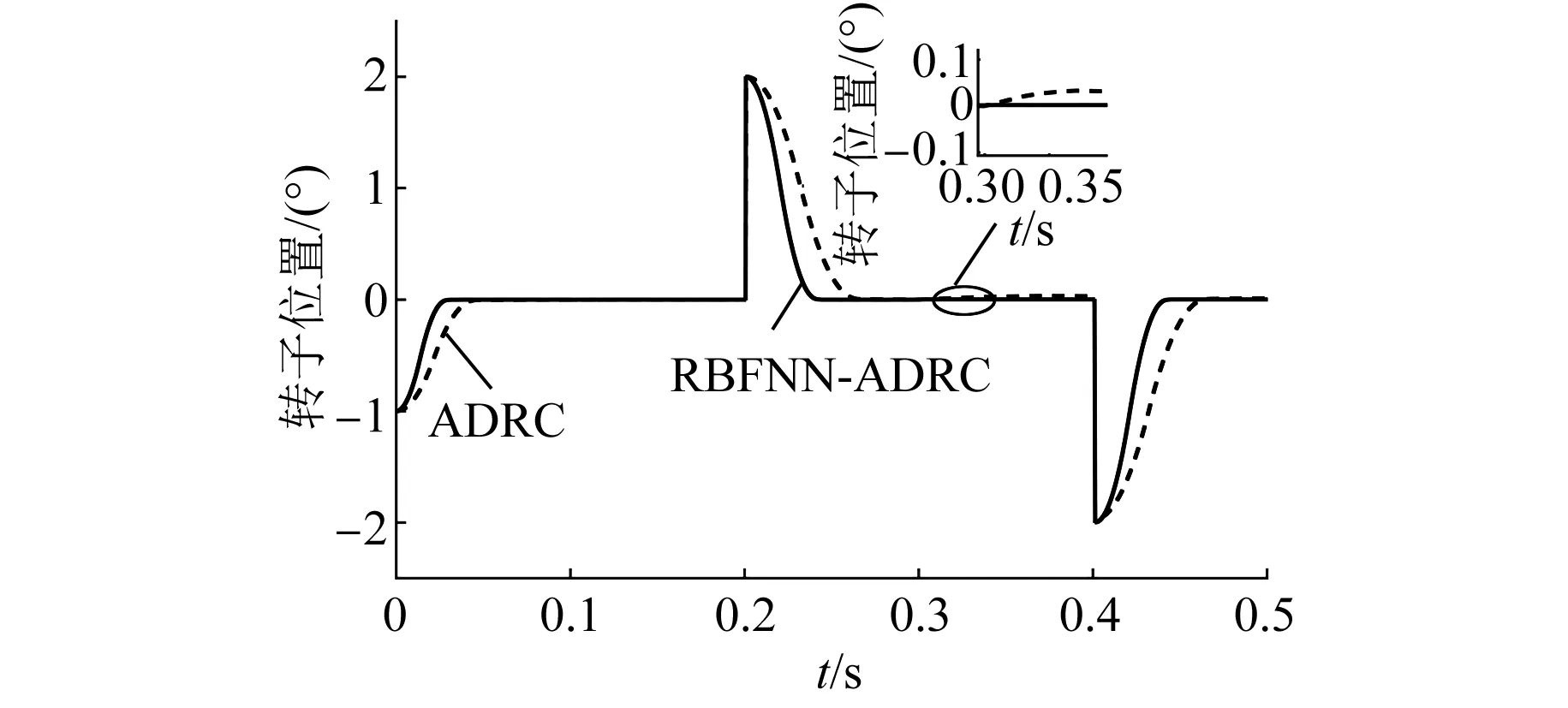
图10 方波输入转子位置跟踪误差曲线

为了更好地对比两种控制方式，以方波输入信号为例，介绍其转速和转矩电流的仿真情况。图11～图13为在方波信号条件下的转速和转矩电流波形。

图11 方波输入转速曲线

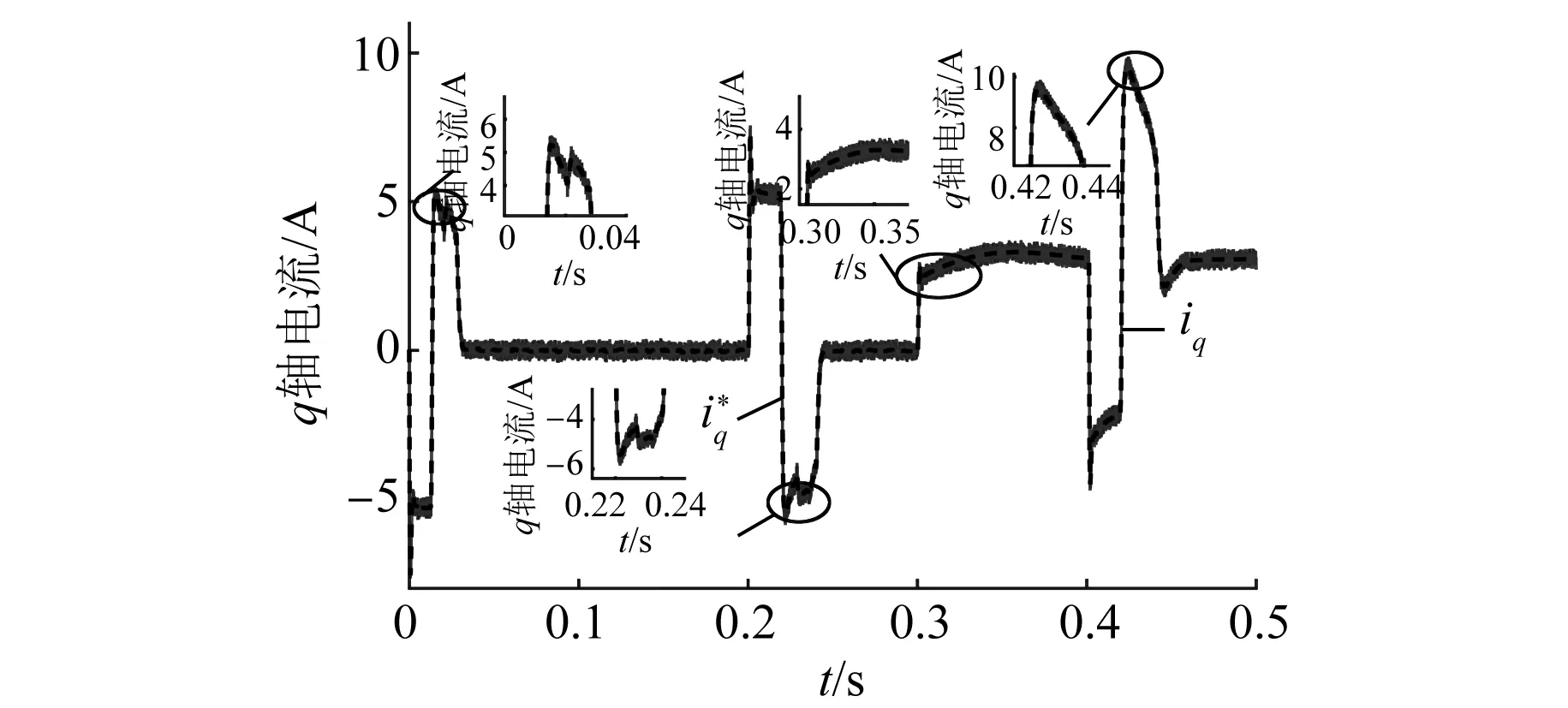
图12 方波输入ADRC电流曲线

图13 方波输入RBFNN-ADRC电流曲线

从图11可以看出，基于传统ADRC的系统在0.3 s突加2 N·m负载后转速跌落至-12.9 r/min，于0.385 6 s才恢复至稳定，并且在0.44 s时出现9.5 r/min的超调；基于RBFNN-ADRC的系统在0.3 s突加2 N·m负载后，转速跌至-6.746 r/min，并于0.305 s恢复至稳定状态，过程平滑且没有超调现象，相较于基于传统ADRC的系统其响应速度更快，正反转控制精度性能更高，且具有更强的抗扰和补偿能力。

图12和图13为系统在方波输入突加负载的条件下转矩电流曲线。两种控制方法的转矩电流给定值和实际值跟踪状态均良好。但是基于传统ADRC的系统在0～0.04 s以及0.21～0.24 s出现了明显的电流振荡，而基于RBFNN-ADRC的系统转矩电流过渡过程平滑。在0.3 s突加2 N·m负载后，基于ADRC的系统响应滞后，在0.40～0.45 s之间，转矩电流出现了明显的电流超调，过渡过程不如基于RBFNN-ADRC的系统平滑稳定。综上所述，基于RBFNN-ADRC的系统比基于传统ADRC的系统具有明显的优越性。

5 结 语

本文的研究对象是PMSM，针对传统ADRC系统需要整定的参数较多且整定过程较复杂的问题，设计了基于RBFNN-ADRC的伺服系统，从而实现ESO中误差增益的参数自整定。通过与基于传统ADRC控制方式的动态及稳态过程进行仿真对比，结果表明，基于RBFNN-ADRC的控制系统具有响应速度快、抗扰能力强、跟踪精度优、稳态误差小等优点。说明了所设计的基于RBFNN-ADRC的伺服系统具有明显的优越性，值得进一步在工程上实现应用。