GIS正常运行与松动故障下的振动机理*

臧 旭, 孙诚斌, 张甜谨, 杨 嵩, 段大卫

(1.国网江苏省电力有限公司镇江供电分公司，江苏 镇江 212000；2.河海大学 能源与电气学院，江苏 南京 211100)

0 引 言

气体绝缘金属封闭开关设备(GIS)作为电力系统高压输电的重要设备，目前在电力系统中的运用越来越广泛。虽然GIS设备的运行可靠性高，但机械故障与绝缘故障也时有发生。据国际大电网会议(CIGRE)统计，GIS常见故障中机械故障占比约44%，GIS的非常见故障中机械故障占比约39%[1-2]。国内统计表明，由安装缺陷、螺丝紧固件松动、触头松脱接触不良等电气连接点松动引发的故障比例约占39.3%，与绝缘故障比例相当，所以有必要对GIS的松动故障进行诊断研究[3-4]。振动法主要应用于开关设备断路器故障或隔离开关动静触头脱落等方面，目前对于GIS机械故障的研究，大多利用振动法测得故障与正常时的振动数据，再通过试验数据挖掘故障特征量(主要是频域特征量)作为故障诊断依据，但都缺少理论的证明与支撑。

文献[5]利用振动法带电检测动触头操作箱对隔离开关的接触状态并进行状态评估，利用频谱分布特征区别是否发生触头的松动故障，但对于振动理论解释较少,且未能给出故障诊断的理论依据，故障诊断特征量提取主要依赖于试验数据，缺少理论层面的分析。文献[6]详细推导了三相共体式与三相分体式GIS的受力振动原理，公式与理论都较为全面，分析了各种引发GIS振动的原因。但对于涡流引发振动以及松动故障引发振动这两类重要的振动原理推导较为简单，未能结合试验或仿真结果证明其理论的正确性，故有必要进一步完善这两种理论下的GIS振动机理。

本文主要对GIS正常与异常运行时的受力振动理论进行更深入的研究，分别从导电杆所受电磁力与涡流两方面推导三相共体式GIS与三相分体式GIS受力振动机理，通过仿真建模证明振动机理的正确性；建立松动故障时接触面受力振动模型，进行受力与运动分析计算；最后结合现场正常与异常运行时的数据频谱特征证明理论的正确性，对GIS受力振动理论进行完善。

1 GIS正常运行时振动原理与仿真

对于GIS管体封装式设备振动机理，目前国内外学者说法不一，本文主要从GIS外壳体上感生涡流在电磁场作用下受力振动和壳体内部载流导体间相互作用力引发振动两方面进行分析，对于文献[7]提到的磁致伸缩效应引发的振动不作考虑，主要因为GIS外壳现在多由铝合金制成，不存在磁致伸缩效应。

1.1 涡流引发壳体振动原理

GIS腔体中的导电杆带电后会在外壳体上感生出感应电动势，通过金属壳体涡流自回路感应产生涡流，在磁场作用下产生电磁力进而引发壳体的振动[8-11]。涡流受力分析示意图如图1所示。

图1 外壳体涡流受力分析图

假设导电杆在外壳内部产生的磁场均匀分布，长导体通以正弦交流电i0=Imcos(ωt)，由安培环路定理求出壳体上磁感应强度：

∮Bdl=μ0μr∑i

(1)

B×2πr=μ0μri0

(2)

(3)

式中：i为环路中电流；i0为导体中流过的瞬时电流；Im为电流幅值;t为时间；B是磁感应强度；μ0是真空中磁导率；μr是相对磁导率；r是某点与导体杆的距离；l为涡流回路从左至右的跨度。

涡流回路中磁通Φ计算如下：

(4)

式中：r2和r1分别为涡流上、下回路与导电杆中心的距离。

计算得到涡流回路的电流ieddy为

(5)

式中：R为涡流回路的电阻。

由此可得壳体上、下部分的受力大小为

(6)

将式(3)和式(5)代入式(6)得到壳体受力最终结果：

(7)

对于GIS壳体，周围磁场的交变频率为电流频率，而壳体受到电磁力的主要频率为2倍的电流频率，电流频率一般是50 Hz，故电磁力与振动频率以100 Hz为主。由式(7)可知，距离导电杆越远导体所受的电磁力越小。

1.2 涡流引发振动的有限元仿真

为验证上述理论的计算结果，利用有限元建立如图2所示的GIS简化模型，并在外壳体靠近内部、外部和中部处选取三个点dot1、dot2、dot3，仿真计算各点处的磁感应强度。

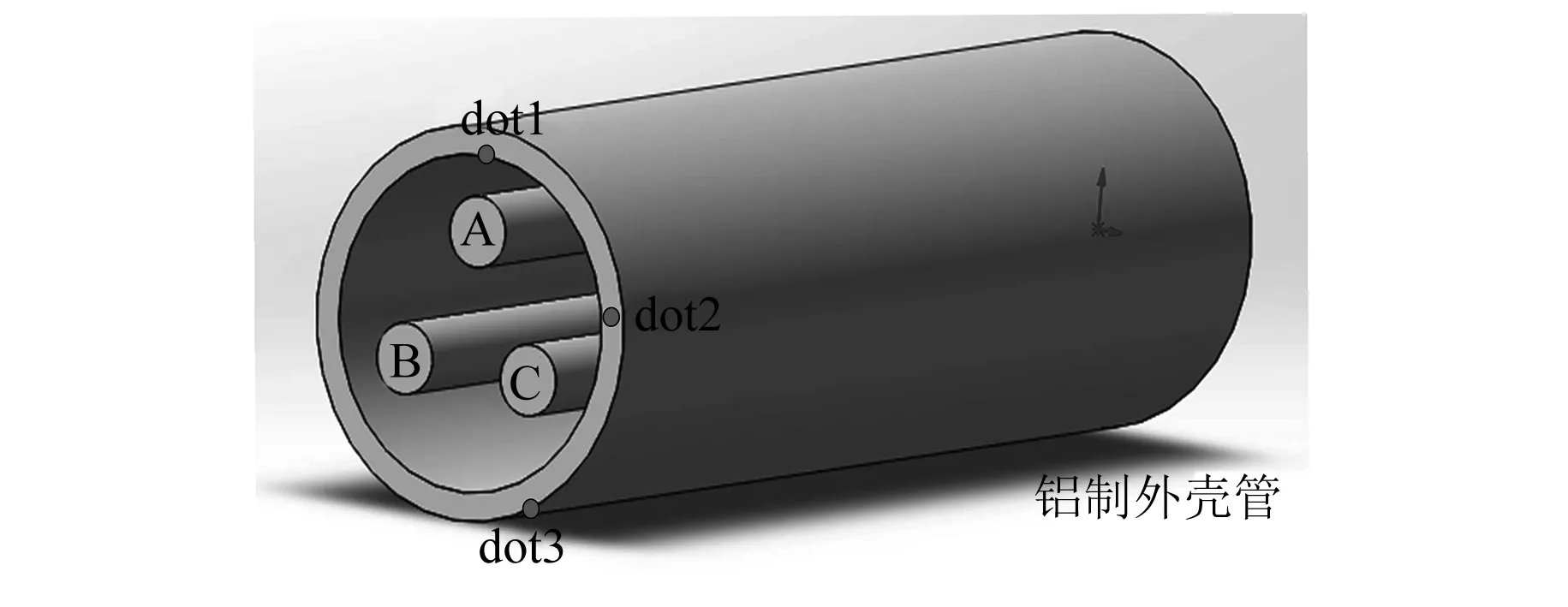
图2 GIS仿真模型结构图

仿真模型中外壳管长度为1.5 m，外壳直径为380 mm，内壳直径为330 mm，导杆直径70 mm，以管体中心为参考点对称分布，相互成120°。GIS的二维瞬态电磁场仿真模型中，采用铝制材料进行仿真计算，考虑交流电作用下金属导体的集肤效应，施加三相对称频率为50 Hz，幅值为800 A的交流电流，仿真步长为1 ms，周期为80 ms，仿真参数如表1所示，得到磁感应强度云图如图3所示。

表1 壳体与金属导体材料及参数

图3 9 ms时母线管断面磁感应强度云图

计算图2中三个点的磁感应强度，绘制关于时间的变化曲线如图4所示。

图4 各点处瞬态磁感应强度

由计算结果可知，壳体上各点处的磁感应强度随时间呈周期性变化。磁感应强度计算取绝对值，因此均在正半轴，实际其变化周期与通入电流的交变周期一致。计算各点所受电磁力的大小，计算结果如图5所示。

由计算结果可知，各点所受电磁力的变化频率为2倍的电流交变频率即为100 Hz，因此仿真所得电磁力变化规律与式(7)的推导结果一致，证明了涡流产生电磁力公式的正确性。

1.3 导电杆受力振动原理分析

GIS腔体中的三相导体在有电流流过时，会在周围产生各自的磁场，从而对邻近的导体产生相互作用力，特别是当导体距离相对较近时，产生的作用力也较明显。对于三相分体式的GIS，铝制外壳的阻隔起到一定的磁场屏蔽作用。但对于三相共体式GIS，由于三相导体布置在同一个金属封闭壳体内，导体间电磁力作用非常明显，这也是引发振动的主要原因[12-15]。以a相导体作为受力研究对象，假设各相导体流过的电流三相对称为ia=Imsin(ωt)，则ib=Imsin(ωt-120°)，ic=Imsin(ωt+120°)。如图6所示，给出a相导体某一瞬间磁场分布图，其中b、c两相对a相的磁感应强度用Bba与Bca表示，三相导体间距离分别为lab、lca、lbc，实际中认为lab=lca=lbc=l。

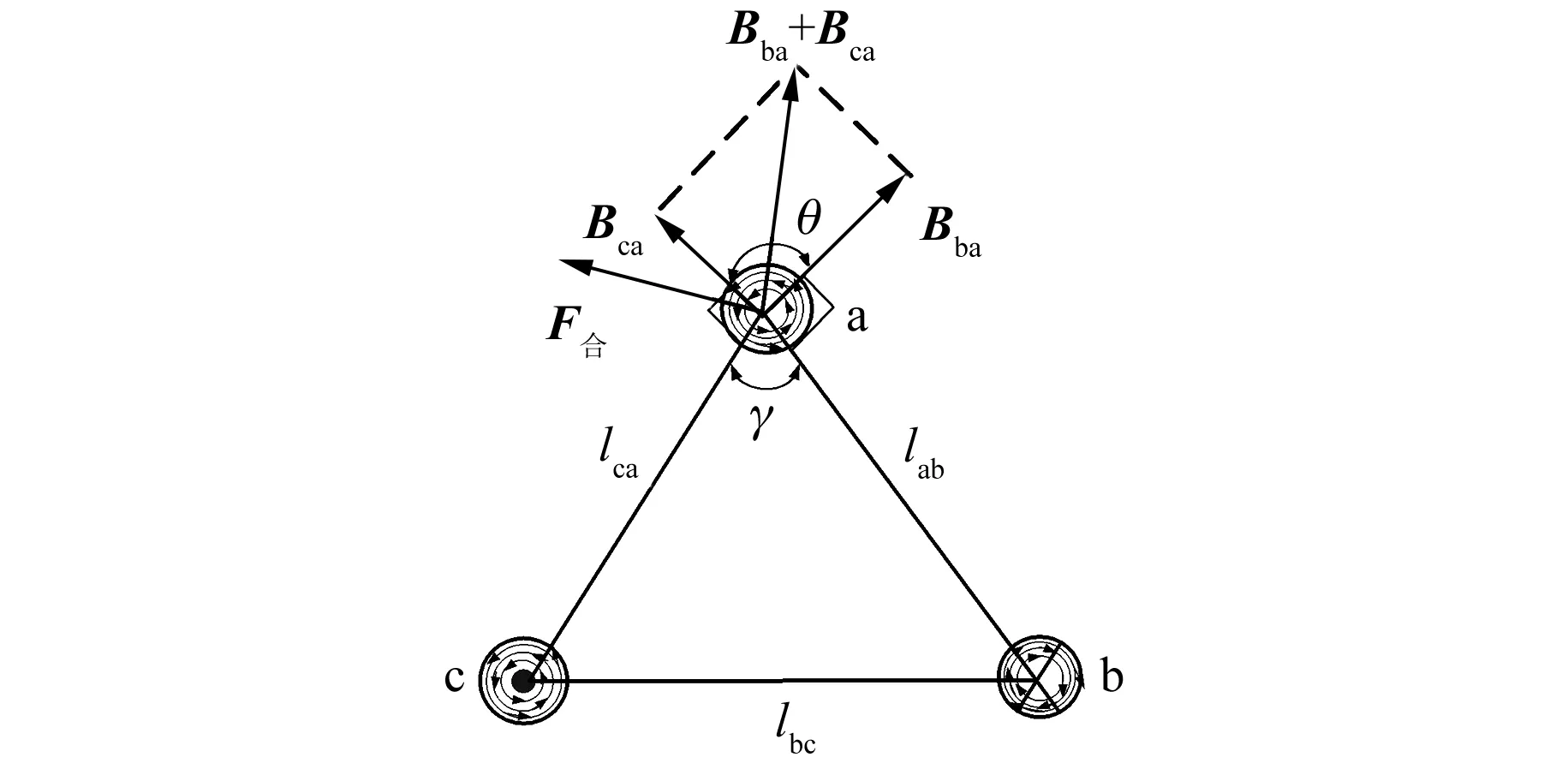
图6 三相导电杆受力示意图

根据无限长导体的电磁感应强度计算公式，b、c相导体对a相导体产生的电磁感应强度分别为

(8)

(9)

由余弦定理计算得到a相导体的合成磁场为

(10)

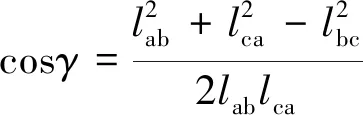
(11)

考虑到lab=lca=lbc=l，将式(8)、式(9)、式(11)代入式(10)，得到：

(12)

假设导电杆a的长度为la，根据电磁力计算公式，可算得导体所受电磁力大小为

(13)

由式(13)可知，GIS导电杆受到的电磁力是周期性变化的，振动频率与电磁力频率一致，为工频50 Hz。因此，对于三相共体式的GIS，导体所受电磁力以50 Hz作为振动的主频率。建立三相导体的电磁场仿真模型如图7所示，仿真参数见表2。

图7 三相导电杆电磁场仿真模型

表2 三相导电杆参数设定

三相导体通入三相对称交流电后，求解a相导体上某点处电磁力大小，如图8所示。由图8可知，0.2 s后仿真计算结果稳定，导电杆所受电磁力交变并且变化周期为0.01 s。由于计算的是电磁力的大小即其绝对值，故实际周期为0.02 s，仿真结果与理论推导一致，证明了式(13)的正确性。

图8 三相导电杆所受电磁力大小

2 GIS异常运行时振动原理与仿真

2.1 GIS松动故障下的振动机理

GIS内部的电气设备较多，机械故障中触头、导杆及电气连接点松动属于常见故障，对于母线、隔离开关、断路器等部件连接点在电流通过时都会发生振动，振动原因是流过接触面上的电流之间的相互作用[16-18]，其受力示意图如图9所示。接触面间属于多斑点式接触，接触点所受电磁力为

F=F0+Fmcos(2ωt)

(14)

式中：F0为恒力；Fm为交变电磁力幅值；ω为电磁力变化角频率；t为时间。

图9 触头接触面受力分析图

接触面的振动可认为是电磁力引起的接触面收缩运动。建立接触面单自由度受力振动模型如图10所示，并进行振动分析。将触点间电磁力收缩振动简化为弹性系数为k，阻尼系数为c的单自由度迫振运动，利用弹簧部分模拟碰撞时的弹性形变，阻尼部分模拟库仑力等产生的阻尼对运动的阻碍作用[19-21]。

图10 接触面受力振动模型

弹性系数k与阻尼系数c和接触点的半径及接触面光滑程度有关，阻尼系数c主要由库仑阻尼引起，与接触点接触紧密程度有关，接触越紧密c越大，当松动间隙变大时阻尼系数减小明显，触点收缩运动方程为

(15)

式中：x为触点间运动位移；m为两侧受力质点。

求解上式的微分方程解：

x1=e-ξωnt[c1cos(ωdt)+c2sin(ωdt)]+

Acos(2ωt+θ)+B

(16)

(17)

式(16)中位移由三部分组成，后面两部分为时不变位移量，作用是使得位移发生周期性变化；前面的位移量是时变位移量，由角频率为ωd的振动位移叠加而成[22-24]。当接触点接触不紧密时，阻尼系数c显著减小，则时变位移衰减缓慢，最终影响触点的运动，从频域分析来说即是振动信号在多个不同频段内的能量均有所增加。

2.2 GIS松动故障下振动仿真计算

上述理论需要进行计算验证。现假设松动时有多个接触点，仿真中取接触点个数为100，认为触点位移均沿同一方向，振动叠加不考虑角度问题，得到如下振动位移计算式：

(18)

选取多组不同的阻尼系数c、弹性系数k，得到不同的角频率ωdi与阻尼系数ξiωni，部分参数如表3所示。

表3 部分仿真参数

仿真得到时域的振动波形图如图11所示，并进行频域变换得到频谱如图12所示。由仿真结果可知，松动类故障会导致某些频率的振动信号幅值增加，并且幅值增加的信号频率是不能确定的，与接触点曲率半径、阻尼系数和弹性系数等多种因素有关。接触点越多，时变位移量衰减越缓慢，各个频段信号能量变化越显著。由计算结果可知，能量增加的主要频段是1 000～2 000 Hz。此外，松动也会导致构件结构改变，使得固有频率变化。

图11 振动位移时域图

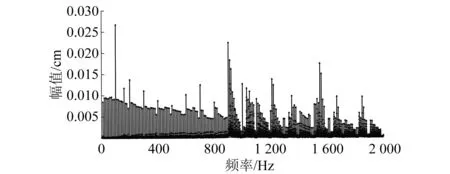
图12 振动位移频谱分析

3 试验对比验证

3.1 试验设置

本次试验是基于型号为ZF7A-126的126 kV三相共体式GIS设备的试验测试，包含了断路器、隔离开关、母线与导电杆等主要一次设备，模拟松动故障，采集松动故障与正常运行时的振动数据。

GIS振动检测系统由压电式振动加速度传感器、1DH5922D动态测试分析仪(最大采样频率为125 460 Hz)及计算机终端组成。振动信号加速度传感器型号为1A212E，其灵敏度为50 mV/(m/s2)，采样频率设置为20 kHz，分别按轴向与径向布置于盆式绝缘子外壁上，布置图如图13所示。

图13 测点位置布置图

本次故障模拟的是母线导电杆松动故障。GIS母线主要起汇流作用，流过的电流较大，振动也较为显著，长期运行下母线导电杆的连接螺丝可能发生松脱。因此，可对母线的固定螺丝进行松脱故障试验，测取正常与异常时GIS外壳的振动信号并进行频谱分析，对比故障前后信号的频谱特征验证上述理论，并进行松动故障的判别与诊断。

3.2 试验结果分析

经过对GIS正常运行与母线导电杆的固定螺丝松动两种状态进行试验，得到这两种状态下的振动时域信号与频域分析结果如图14所示。

固定螺丝松动时，时域信号的振动幅值相比正常时显著增大。对比图14(b)和图14(d)即正常与松动故障时1 000～2 000 Hz的频域信号幅值，可知故障时该频段信号幅值是增大的。该频段的信号幅值增加与故障位置和故障类型有关，这与上述的松动故障下振动位移仿真结果一致，因此也可将该频段信号的幅值变化作为故障判断的特征依据。

图14 正常与异常运行时测点振动信号

4 结 语

(1) 本文分析了GIS外壳涡流引发振动的原理及壳内导体间电磁力作用的振动原理，分别进行仿真分析以验证GIS的受力情况与振动变化规律，结果表明正常运行时的GIS设备振动频率为100 Hz或者50 Hz都有可能，这是GIS设备的受力原理不同所导致的。

(2) 母线导电杆发生松动故障时，GIS外壳振动信号中1 000～2 000 Hz的频段信号幅值有所增加。这一结果与GIS松动故障下的仿真计算具有相似性，可以为后续GIS松动故障的研究提供理论依据，也可作为提取故障特征的参考为松动类机械故障诊断提供有效的判别方法。