基于大容量样本挖掘及贝叶斯堆栈泛化集成算法的电站锅炉NOx稳态建模

2022-08-31朱宇坤张梯华刘红娇司风琪

热力发电 2022年8期

朱宇坤，喻聪，张梯华，刘红娇，司风琪

（1.江汉大学智能制造学院，湖北武汉 430056；2.东南大学能源热转换及其过程测控教育部重点实验室，江苏南京 210096）

“十四五”规划及2035远景目标指出[1]，推进能源革命，构建清洁、低碳、安全、高效的能源体系是新时代的必由之路。在电力系统中，火电机组具备调峰调压的能力，是较为稳定的能源供应方式，但其也存在高污染的问题。因此，控制燃煤电站锅炉氮氧化物（NOx）等污染物的排放量尤为重要。这就需要建立准确的预测模型，对炉内燃烧方式进行优化控制。

目前炉内燃烧生成NOx质量浓度的预测方法大致分为机理建模和数据驱动建模2种。机理建模主要是采用计算流体力学方法建立锅炉燃烧及换热过程的数值模型，这种方法能够获得炉内流场、化学氛围、温度等信息的分布特征，从而分析燃烧调整方式与污染物生成量的内在关系[2-4]。然而，大型电站锅炉的数值模型往往会基于一些理想的假设条件建立，炉内积灰、结渣、管内氧化膜的分布和变化等实际环境中的复杂因素无法全面考虑。此外，机理建模方法需要迭代求解大量偏微分方程，计算耗时较长[5]，这也限制了数值模型在现场实时燃烧优化过程中的应用。

随着计算机的快速发展，大量工业运行数据的收集和保存促进了数据驱动模型的发展。数据驱动模型能直接从运行数据中学习参数间的关系，拟合能力强，且模型训练完成后，一般具有较快的预测速度。Zhou[6]、Zheng[7]、刘延泉等[8]分别利用人工神经网络、支持向量机和最小二乘支持向量机建立了NOx的排放特性模型，并结合智能算法优化了模型的超参数。这些模型均能取得较好的预测效果，但模型多是基于试验数据建立，样本数量有限，而电站锅炉的建模是涉及多变量的高维问题，这会使模型在某些远离试验工况的空间中没有足够的训练样本，从而使泛化能力降低。笔者曾将试验数据中得到的先验知识融入NOx的数据驱动建模中[9]，但模型学习的依然只是试验数据中的知识。周昊等[10]也指出采用人工选择的小样本建模可能造成模型泛化能力的下降及有用信息的丢失。

近年来，学者们逐步开始研究基于历史运行数据的电站锅炉大容量样本建模方法。Tan等人[11]利用长短时记忆（long short-term memory，LSTM）神经网络建立了NOx的预测模型，并通过调节学习率和隐藏节点数等超参数优化了模型的性能。唐振浩等[12]采用融合误差校正的极限学习机建立NOx质量浓度动态预测模型。Wang等人[13]在LSTM模型中加入注意力机制，并采用网格搜索和Adam算法确定了模型最优的超参数，对NOx质量浓度进行了预测。刘菡等[14]基于互信息-图卷积神经网络建立了燃煤电站NOx排放质量浓度的预测模型，这些时序预测模型能在锅炉动态变化的过程中，实时准确地预测当前及未来某时刻的NOx质量浓度，可应用于电站烟气在线监测系统（con-tinuous emission monitoring system，CEMS）测点的故障诊断，但模型的重点不是描述锅炉调节变量和NOx质量浓度的静态关系。

本文以某660 MW机组燃煤电站锅炉72 000条历史运行数据为样本，提出了适用于燃烧优化调整的NOx静态特性模型。首先利用孤立森林算法和R-Values检验算法处理离群点及非稳态数据，获得高质量的稳态样本集；在此基础上，采用递归特征消除法对影响生成NOx的关键变量进行特征选择，进而考虑单一模型的局限性，提出了以支持向量机、极端随机树、梯度上升树为基模型，以线性回归为二级模型，以堆叠策略为集成方法，以贝叶斯优化为寻优算法的NOx预测模型。

1 算法简介

1.1 模型框架

图1为本文提出的NOx静态预测模型框架，该模型主要步骤如下。

步骤1 大容量样本挖掘。从电站厂级监控信息系统（supervisory information system，SIS）中获得历史运行数据。采用R-Value检验法[15]为每个数据标记稳态标签（0为稳态数据，1为非稳态数据），采用孤立森林[16]（isolation forest，IForest）算法为每个数据标记离群点标签（0为非离群点，1为离群点），为每个数据标记停滞点标签（0为数值正常变化的数据，1为因传输故障而停滞不变的数据）。对于每条样本，若样本中每个维度的数据的稳态标签、离群点标签、停滞点标签均为0，则这条样本为正常稳态样本，存入稳态样本库，反之剔除，最终得到蕴含系统稳态信息的高质量稳态样本库。

步骤2 特征选择。考虑到特征提取算法是从原始特征中创建无实际物理意义的新特征，难以直接用于锅炉可调变量的燃烧优化调整。本文采用随机森林递归特征消除（random forest-recursive feature elimination，RF-RFE）算法[17]对步骤1得到的高质量稳态样本库进行特征选择，并经过归一化处理得到模型的训练集和测试集。

步骤3 基模型的训练及超参数优化。电站锅炉NOx质量浓度的预测是高维、非线性的回归问题，训练时容易过拟合。考虑到支持向量回归机（support vector regression，SVR）具有较好的泛化能力，极端随机树（extremely randomized trees，ET）算法[18]能够针对特征随机的分裂行为避免模型的训练陷入局部最优，梯度上升树（gradient boosting decision tree，GBDT）算法[19]能够发现特征间的高阶关系，选择这3个模型作为集成学习的基模型。在此基础上，确定各个基模型中参数优化的范围及优化算法的终止条件，并利用贝叶斯优化（Bayesian optimization，BO）算法[20]搜索基模型的最优超参数。

步骤4 基模型的集成及二级模型的训练。为进一步增强模型泛化能力，采用堆栈泛化集成学习模型（stacking generalization ensemble model，SGEM）[21]对3个基模型的预测结果进行融合，并采用线性回归（linear regression，LR）作为二级模型完成对NOx质量浓度的预测。

1.2 基于R-Value的稳态诊断

R-Value检验算法因其流程简单、精度良好而被广泛应用于工业过程数据的稳态判定。对于某个时刻的数据Xf,i，通过计算和构建稳态判定的检验指标R，计算公式为：

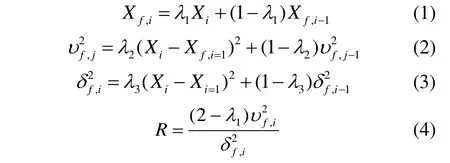
式中：λ1、λ2、λ3的值分别为0.2、0.1、0.1。

1.3 基于IForest算法的异常点诊断

IForest算法是由大量孤立树（isolation tree，iTree）构成，它是利用群体表决的方法进行离群点的判定。算法主要包括2个部分：第1部分是生成树，建立孤立森林；第2部分是对被检测的样本计算异常分值。

1）建立孤立森林

步骤1 从训练数据中随机选择ψ个样本作为样本子集，然后放入该树的根节点。

步骤2 随机指定一个特征，在此节点的数据中随机产生一个切割点p，该切割点必须位于所选择特征中所有数据最大值和最小值之间。

步骤3 通过该切割点延展成一个超平面，然后将当前节点的数据空间分割成2个子空间。在所指定的特征中，将数值小于p的数据放在当前节点左边，大于p的数据放在当前节点右边。

步骤4 通过不断递归步骤3和步骤4，直到满足其中一个终止条件：1）各子空间数据不可分；2）iTree树的深度已达到了log2ψ。

2）计算异常得分

获得由n棵iTree组成的孤立森林后，利用IForest评估测试数据，即遍历每棵iTree，获得样本在每棵树的深度，然后计算出该数据点在森林中的平均深度，最后将平均深度进行相应的数据变换就可以得到该数据点所对应的分数。异常得分与深度相关，深度越大，异常得分越小，反之亦然。计算异常得分的公式为：

式中：h(x)表示被检测样本在iTree中节点所处的深度；E[·]表示取平均值；c(ψ)表示ψ个样本点所构建的二叉树的平均路径长度；h(k)=ln(k)+ζ，ζ为欧拉常数；s(x)得分越靠近1，数据异常的可能性越高；s(x)得分越靠近0，数据正常的可能性越高。

1.4 基于RF-RFE的特征选择

RF-RFE算法是首先构建随机森林回归模型，计算每个特征的重要性并排序，再引入基于后向迭代的特征评价标准，删除重要性较小的特征，继而重复上述操作，直到特征只剩下1个，最后根据均方误差的大小选择最优的特征组合。

1.5 基于BO-SGEM的NOx预测

利用贝叶斯优化算法对SVR、ET、GBDT 3个基模型进行调参，再利用SGEM融合基模型预测结果，最后以线性回归为二级模型对NOx质量浓度进行预测。

1.5.1 SVR

SVR模型可定义为：

式中：w为权重；b为截距；ϕ(x)为将样本映射到高维空间的映射函数。

为了求解w和b，引入松弛变量iξ、*iξ和惩罚系数C，得到模型的训练问题：

将式(8)转变为其对偶优化问题：

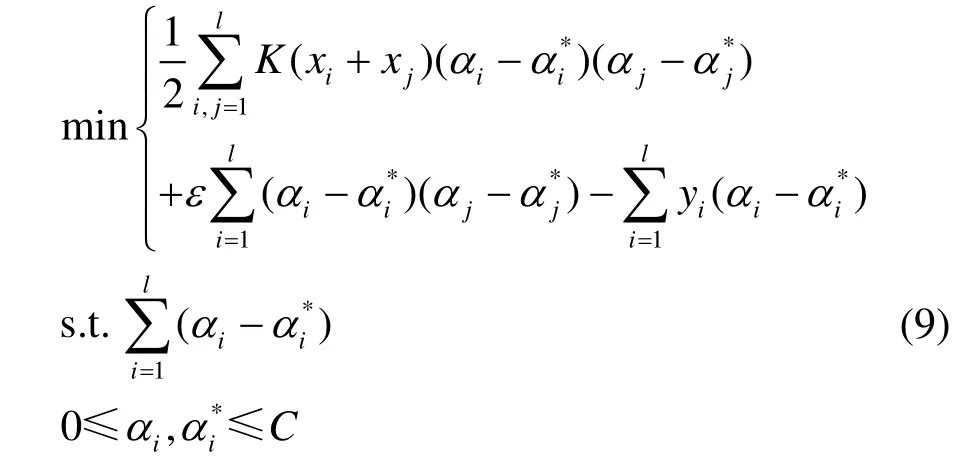
式中：αi和均为拉格朗日乘子；K(xj,xi)为核函数。

求解式(9)，得到SVR的回归函数：

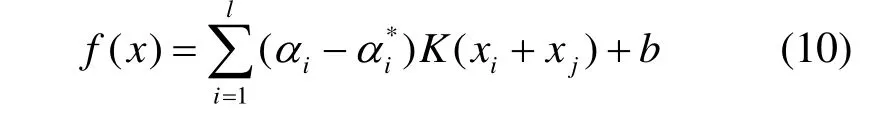
1.5.2 ET

ET算法是随机森林算法的一个变种。相较于随机森林，ET算法是随机选取原始训练集的子集作为训练集，并根据基尼系数等指标选择最好的特征进行划分，ET算法中每棵决策树都采用原始训练集训练，而在划分特征时随机选择1个特征来划分决策树。由于ET算法不是选取最优特征进行分裂，ET算法中树的规模比随机森林更大，但模型的方差更小，在某些时候的泛化能力比随机森林要好。

1.5.3 GBDT

GBDT的算法流程如下：

步骤1 假设模型训练的样本集合T为：T={(x1,y1), (x2,y2), … , (xn,yn)},xi∈X⊆Rn,yi∈Y⊆R。

初始化弱学习器：

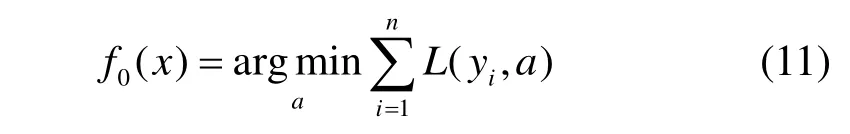
式中：L为损失函数；n为样本总数。

步骤2 开始最大次数为N的迭代求解。首先计算当前损失函数的负梯度，并以此作为样本残差的近似值：

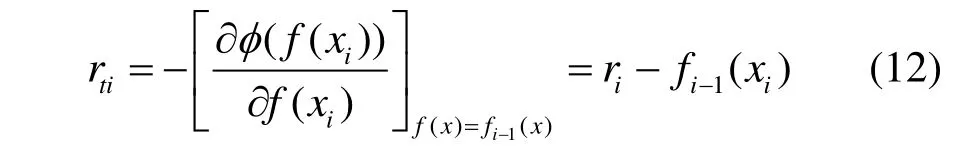
步骤3 将步骤2所计算的残差作为新的数据，拟合1棵回归树，得到与之对应的叶子节点的集合为Rjt，j=1, 2, 3 ,…,J。

步骤4 对每个叶子区域j=1, 2, 3 ,…,J，求极小化的损失函数：

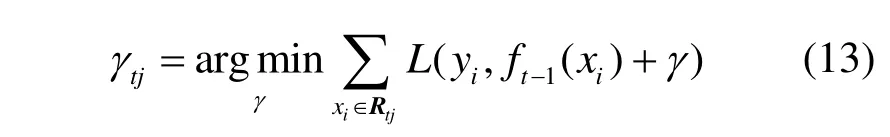
步骤5 利用前一模型的预测结果更新当前模型的预测结果：

步骤6 完成迭代，得到最终GBDT模型：

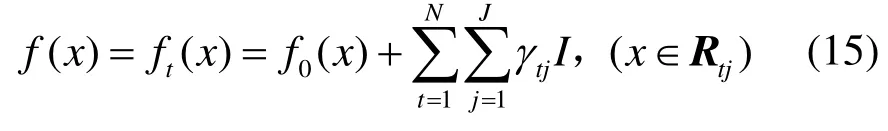
1.5.4 SGEM

SGEM的训练过程如图1所示，步骤如下。

步骤1 首先将原始数据集划分为训练集（train）和测试集（test）。再采用K折交叉验证法将训练集分为K份，本文K=5，故将训练集分为5个子集，分别记为TD1、TD2、TD3、TD4和TD5。

步骤2 将TD1—TD5中的任意4组作为训练数据，剩余1组作为测试数据，对每种基模型分别训练5次。对于一种基模型，利用5次训练得到的模型分别对5组测试数据和1组测试集进行预测，分别得到Pre1、Pre2、Pre3、Pre4、Pre5和P1、P2、P3、P4、P5。

步骤3 将每种基模型预测得到的Pre1、Pre2、Pre3、Pre4、Pre5堆叠在一起，组成新的训练集。将每种基模型预测得到的P1、P2、P3、P4、P5分别取平均，得到各自的Pre6，堆叠在一起作为新的测试集。

步骤4 以新的训练集和新的测试集为样本，以线性回归为二级模型，建立NOx的预测模型。

1.5.5 BO

BO是一种近似逼近的方法，在全局优化方面效果较好。它是基于贝叶斯公式(16)对目标函数f进行评估，找到一个能使全局提升最大的下一个参数组合结果，从而快速逼近最优解，找到最佳的超参数组合。其计算公式为：

式中：f为目标函数；D为已观测的集合D={(x1,y1),(x2,y2), …, (xt,yt)}；xt为决策变量；yt=f(xt)+ζt为观测值；ζt为观测误差；p(f|D)为f的后验概率分布；p(f)为f为的先验概率分布，即对未知目标函数状态的假设；p(D|f)为f的边际似然分布。

2 NOx静态预测模型的建立

2.1 数据预处理

选择某660 MW机组四角切圆燃煤电站锅炉的72 000个历史运行数据为分析样本，采样间隔为30 s。其中机组负荷的变化范围为330～660 MW，涵盖了负荷上升、下降、稳定等各种工况范围，具有很强的随机性和代表性。

基于R-Value法计算每条样本的稳态因子，通过对比不同稳态阈值的合理性，得到每条样本的稳态标签。在此基础上，计算每条样本的停滞点标签及离群点标签。通过标签剔除非稳态样本、离群点样本、停滞点样本后，剩余6 985条高质量稳态样本作为NOx预测的样本集。随机选择样本集中70%的样本（4 889条）作为训练集，其余30%（2 096条）作为测试集。

采用式(17)对各维变量进行归一化，消除不同变量量纲之间的差别对建模的影响：

式中：x为原始数据；xn为归一化后的数据；xmax和xmin分别为原始数据的最大值和最小值。

2.2 NOx的预测

锅炉的设计、运行调整和燃用煤种对NOx的生成有很大影响。对于设计参数已经固定的锅炉，运行方式和燃煤特性是影响NOx生成的重要因素。电站大多数燃煤根据期望的要求混合良好，其特性在一段时间内保持大致稳定，本文锅炉长期使用淮南烟煤，煤质成分和热值变化不大。此外，燃煤特性可以通过运行参数反映。因此，本文排除燃煤特性的影响而只关注运行参数。以选择性催化还原（selective catalytic reduction,SCR）脱硝反应器A、B入口平均NOx质量浓度作为预测目标，以机组负荷、总煤量、一次风压、总风量、氧量、给水流量、SOFA风门摆角、5层SOFA风门开度、2层CCOFA风门开度、18层一、二次风门开度作为影响NOx质量浓度的32个初始变量。

3 结果及分析

3.1 数据预处理

3.1.1 稳态判定

图2为采用R-Value算法对氧体积分数和总风量在一段连续时间内的数据进行稳态判定的结果。

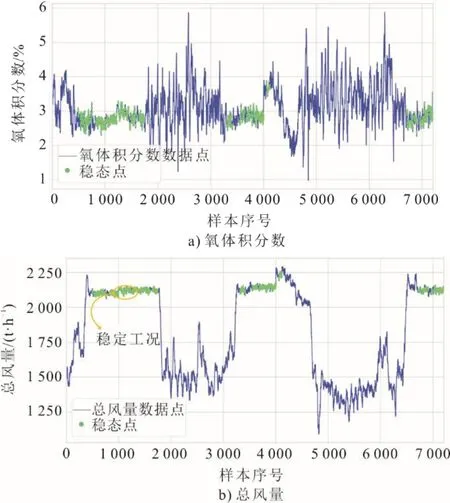
图2 基于R-Value算法的稳态判定结果Fig.2 The steady-state determination result based on RValue algorithm

由图2可见，该算法基本能将数据中平稳段识别出。剔除非稳态数据后，数据由72 000条变为8 218条。

3.1.2 离群点剔除

图3对比了LOF[22]、OCSVM[23]、ABOD[24]、KNN[25]、IForest[15]、HBOS[26]、MCD[27]、PCA[28]和Feature Bagging[29]9种算法在相同数据集下识别离群点的结果。由图3可知，OCSVM、KNN、IForest、HBOD和MCD对模型边界识别较好，其中IForest和HBOS误分类个数为0。然而，HBOS对于小样本容量和较少特征参量的情况预测效果更好，随着数据量和数据维度的增大，IForest的优势更为明显，不仅识别速度快，识别精度也更高。考虑到本文是大容量样本、高维度的建模问题，因此选用IForest算法进行离群点诊断。剔除非稳态数据后，继续剔除离群点和停滞点共1 235条，最终得到高质量稳态样本6 985条。

图3 9种算法识别离群点结果Fig.3 The outlier point identification results using nine algorithms

3.1.3 特征选择

32维与NOx质量浓度相关的输入变量间包含大量冗余、共线和重叠的信息。利用所有变量建模不仅耗时，同时噪音和无用信息也会影响模型精度和鲁棒性。为了得到能反映绝大部分信息的特征，本文采用RF-RFE进行特征选择，代入经非稳态值和异常值剔除后的6 985条样本，得到不同特征个数下的交叉验证得分，结果如图4所示。

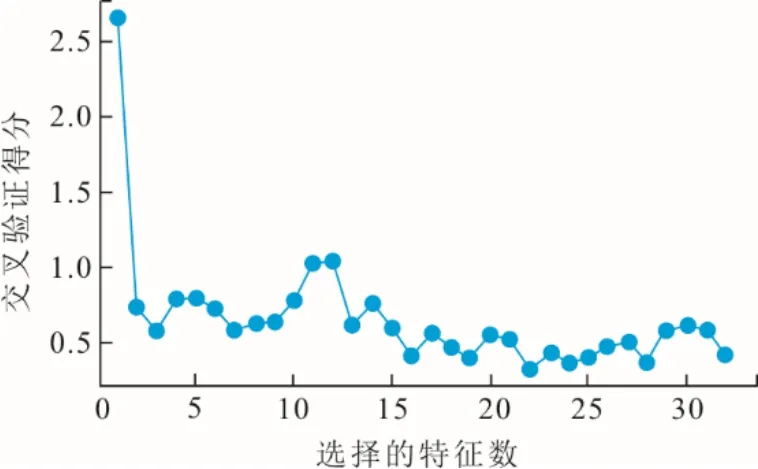
图4 选择特征数与交叉验证准确性的关系Fig.4 Relationship between the number of selected features and the accuracy of cross-validation

由图4可见，当选择特征数为22时，得分最低，效果最好，因此最终选择机组负荷、一次风压、给水流量、氧量、SOFA-I开度、SOFA-II开度、SOFA风摆角、CCOFA-I开度、CCOFA-II开度、AA开度、AB开度、CD开度、BC开度、C开度、D开度、DE开度、E开度、BI/BII开度、AI/AII开度、EI/EII开度、F开度、FI/FII开度22个变量作为NOx预测模型的输入参数。机组负荷和煤量存在相关性，煤量和风量的比例又能决定氧量。经RF-RFE特征选择后，存在重叠关系的这2个变量被约简为机组负荷和氧量2个变量，这也证明了该算法的合理性。

3.2 预测结果分析

得到6 985条高质量稳态样本及确定模型22维输入特征后，采用BO对SGEM 3个基模型SVR、ET和GBDT的参数进行寻优，最大迭代次数均设置为500，图5、图6、图7分别为SVR、ET和GBDT算法的超参数迭代过程。其中BO算法寻优的目标值为均方根误差，该值越小越好。由图5可知，当SVR算法超参数C在1～1 000、gamma在0.001～1时，目标值达到最小。由图6可知，当ET算法的超参数min_samples_leaf在0附近时，目标值明显收敛到最小，而max_depth和n_estimators在各个数值范围均能使目标值达到最小，说明这2个参数对本文所建ET模型的精度影响不大。由图7可知，当GBDT算法中的超参数max_depth在0～100、n_estimators在200～300、min_samples_leaf在200～400时，目标值收敛到最小，说明GBDT模型3个超参数的取值均对模型的精度有着重要影响。

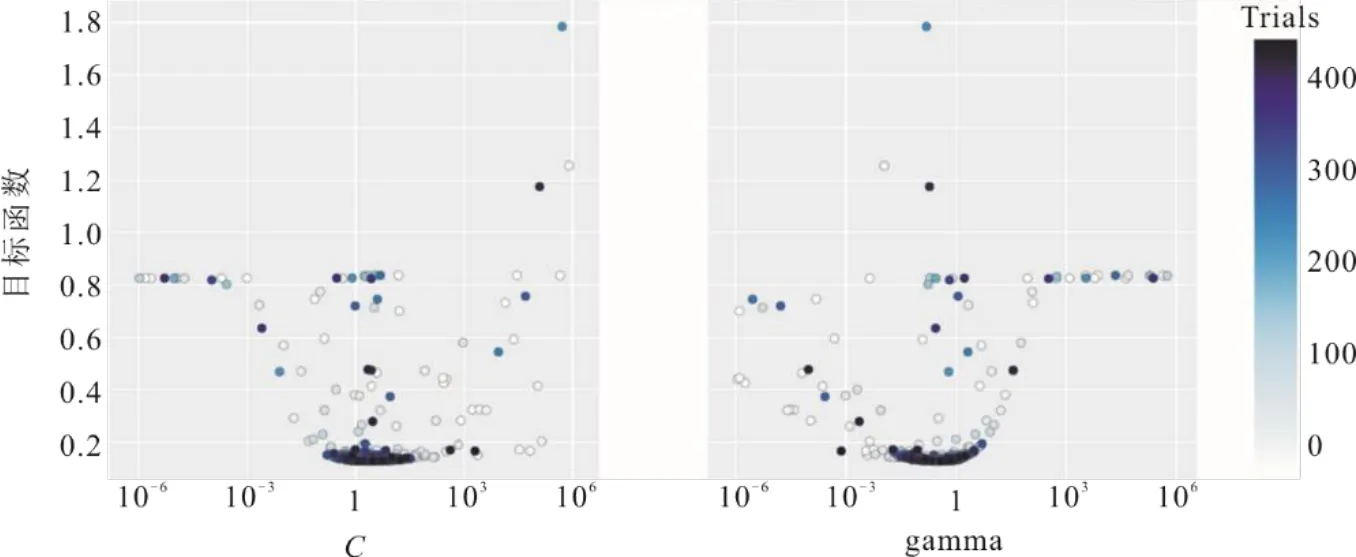
图5 SVR算法的超参数迭代过程Fig.5 The hyper parametric iterative graphs for SVR algorithm

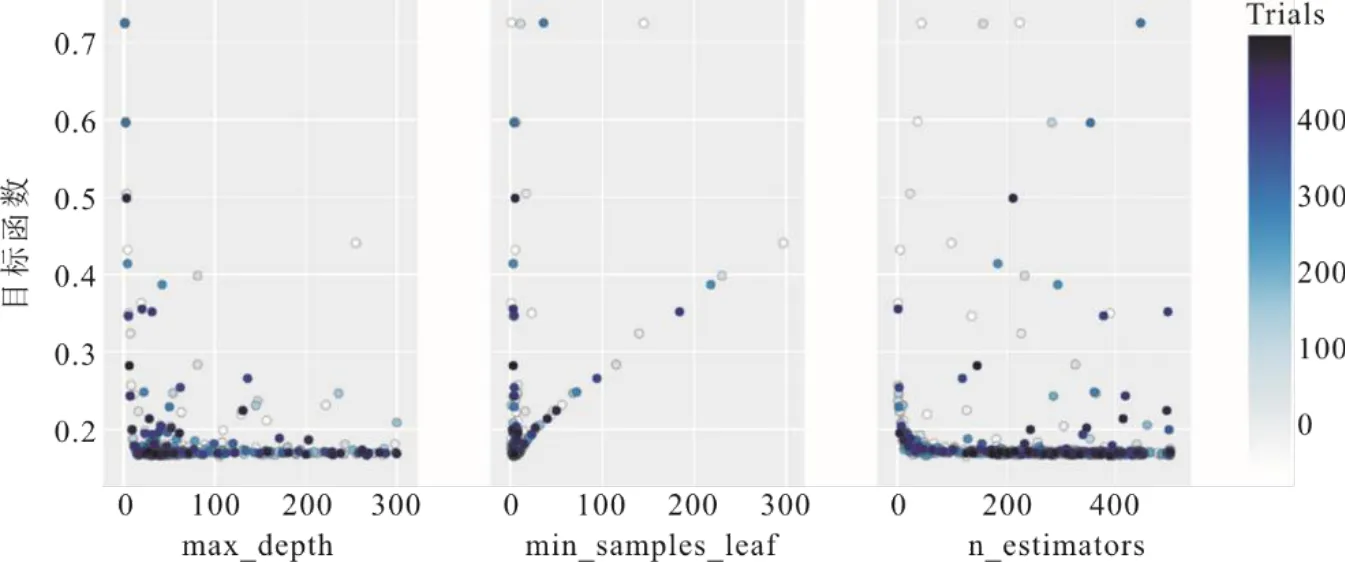
图6 ET算法的超参数迭代过程Fig.6 The hyper parametric iterative graphs for ET algorithm

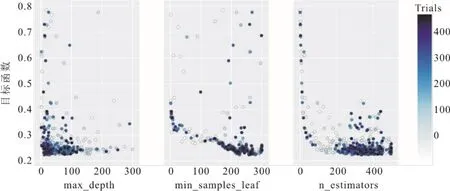
图7 GBDT算法的超参数迭代过程Fig.7 The hyper parametric iterative graphs for GBDT algorithm

寻优得到的基模型最优超参数见表1。为了进一步验证BO算法的效果，将经过贝叶斯优化后的模型参数代入SGEM模型，并与未调参的SGEM模型进行比较，结果见表2。

表1 BO-SGEM模型参数Tab.1 Parameters of the BO-SGEM model

表2 BO-SGEM与SGEM模型比较Tab.2 Comparison between the BO-SGEM model and the SGEM model

由表2可知，BO-SGEM模型在训练集的R2和δMAE分别为0.963和2.995，优于SGEM模型在训练集上的δMAE（0.958）和R2（3.265）。测试集上BO-SGEM模型的R2和δMAE也比SGEM模型好。因此，经过BO模型参数寻优后，SGEM模型的性能变优。

为了分析SGEM算法的效果，本文对比SGEM集成模型和SVR、ET、GBDT模型对相同数据集的预测结果。图8给出了SGEM集成模型和基模型对测试集NOx质量浓度预测结果。由图8可知，从整体来看，4种模型的预测趋势对测量值的变化趋势均跟踪较好，SGEM模型的预测结果与真实值更加接近，其变化趋势也更符合真实情况。同时，SGEM模型的性能更为稳定，GBDT模型在这2个区间出现了波动，在某些区域与真实值相差过大。由于测试集包含了机组负荷在330～660 MW的不同工况，SGEM模型预测结果均较好，可认为SGEM模型能有效处理复杂变化环境中的NOx预测问题。

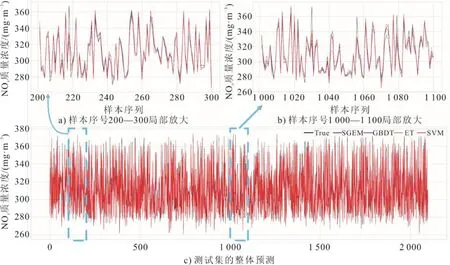
图8 SGEM和基模型对测试集NOx质量浓度预测结果Fig.8 The predicted results of testing sets NOx mass concentration by SGEM and base models

图9为4个模型的误差分析结果。由图9a)可知，4种模型的相对误差均近似呈现以0为均值的正态分布。相较于ET和SGEM模型，SVR和GBDT模型预测结果偏离真实值的点明显更多。而相较于其他3个算法，GBDT模型的相对误差大于5的频率最高。

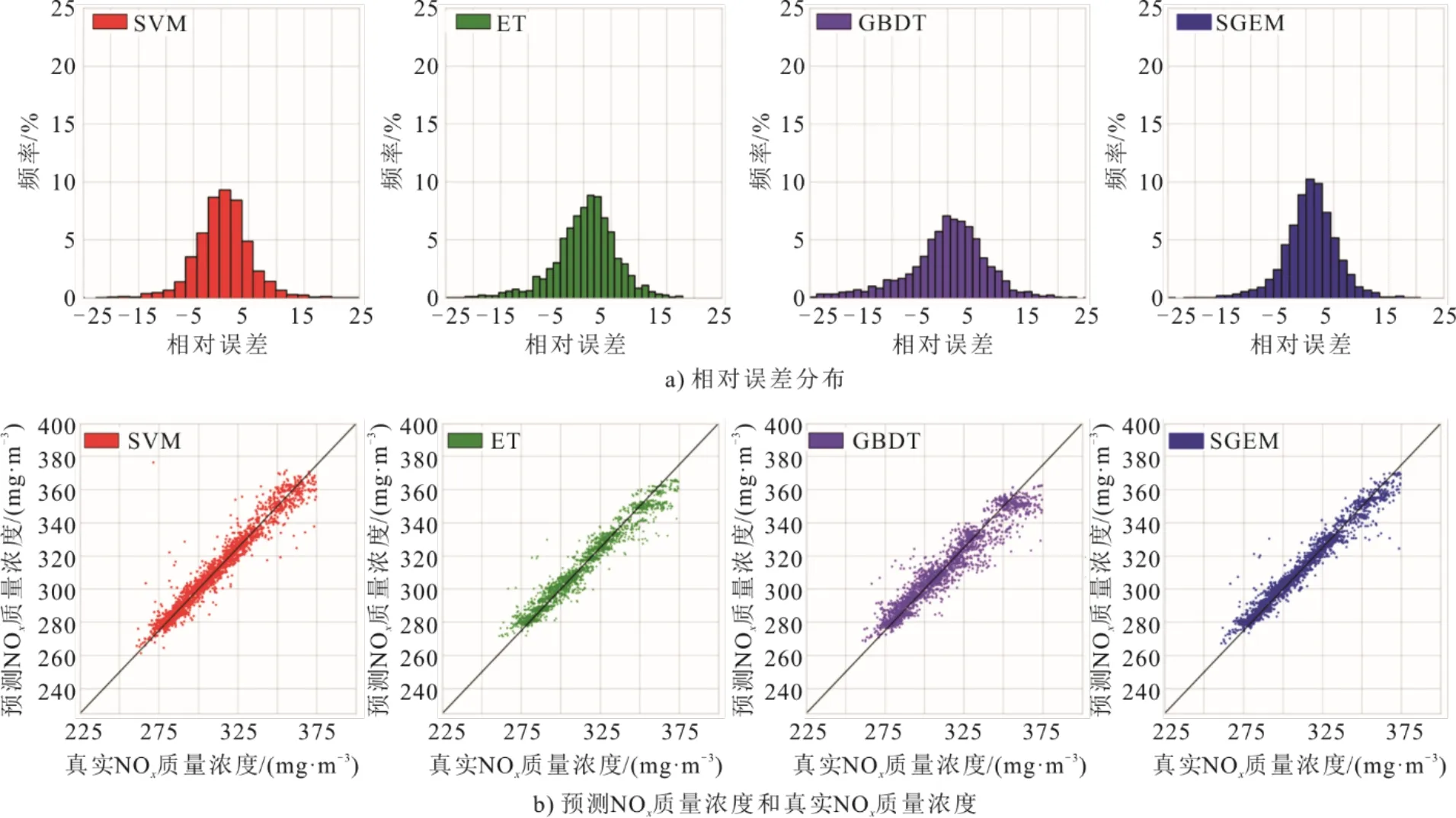
图9 4种模型相对误差分布和实际、预测的NOx质量浓度比较Fig.9 The relative error distribution diagram of four models and the actual and predicted values of NOx mass concentration

SVR、ET和SGEM模型相对误差小于5的频率分别为0.750、0.687和0.765，且相对误差小于3的频率分别为0.524、0.481和0.529，结果表现出SGEM模型最优，SVR模型次之，两者均优于ET模型。综上所述，SGEM模型的性能优于SVR、ET和GBDT模型。