基于载波移相的MMC改进均压控制策略

王慧茹，陈 卓，刘人志，滕 飞，罗 茜

（贵州大学 电气工程学院，贵州 贵阳 550025）

0 引言

随着智能电网的发展，电力电子变压器（power electronic transformer，PET）因其能实现电压变换、无功补偿和可再生能源接入的功能而成为电力电子领域的研究热点[1-4]。模块化多电平换流器 （modular multilevel converter，MMC）因其具有模块化和高压直流端口的结构特点，而被应用到PET的整流级，从而实现了可再生能源的直流接入和网络的中压直流输电；这对新能源的并网及就地消纳具有重要意义[5]。

作为输入级的MMC，其子模块均压效果直接影响到下一级能否获得稳定的直流母线电压。因此，MMC的电容电压均衡控制是必须要解决的问题。

针对电容电压均衡，目前最常用的2种调制策略为最近电平逼近调制和载波移相调制[6]。最近电平逼近调制控制因其方法简单、开关频率低而得到了广泛的应用[7]；但该方法在应用于子模块数较少的场合时，会因电平数少而导致电网电流谐波含量大[8]。载波移相调制策略的特点是具有固定的开关频率，而且可以获得较高的等效开关频率；该方法应用于子模块数较少的场合时，电网谐波含量低[9]。

关于最近电平逼近调制的排序均压算法，很多文献已经做出了深入的研究[10]；但针对应用在子模块数较少的、基于载波移相调制的均压策略的研究相对较少。

以下文献结合载波移相调制对 MMC的电压均衡控制策略进行研究。

文献[11]提出传统电容电压均衡控制策略：通过在参考电压信号上叠加控制环节产生的电压均衡调制量，实现电容电压的均衡；控制环节的核心是PI控制和比例控制。该控制方法虽然简单有效，但电容电压的一致性较差。

文献[12]提出了基于能量平衡的控制策略——从能量平衡的角度出发，通过公式计算得到环流参考值。该策略避免了PI参数繁琐的整定过程，提高了系统的暂态性能；但其控制环流环节采用比例重复控制算法，一般需要在数字信号处理器（DSP）中实现[13]。

文献[14]根据线性化方法下的电容电荷转移规律，设计了新型的电压平衡算法；其优点是无需测量桥臂电流。

上述文献研究成果虽然在一定程度上实现了电容电压的均衡，但对电容电压的一致性没有做深入讨论。

本文，首先基于 MMC的工作原理，对电容电压不均衡的原因进行了分析；然后，针对传统均压控制策略存在的一致性差的问题，在传统策略的基础上，引入桥臂电容电压平均值前馈控制，以提高电容电压的一致性；最后，通过仿真实验，验证该策略的正确性和有效性。

1 MMC的工作原理

1.1 拓扑结构

图1为模块化多电平整流器的三相拓扑结构。从图1中可以看出，MMC三相电路的三个相单元的结构完全相同，都由上、下2个桥臂组成；每个桥臂又由n个结构和参数完全相同的子模块、桥臂电感L以及桥臂等效电阻Req组成。

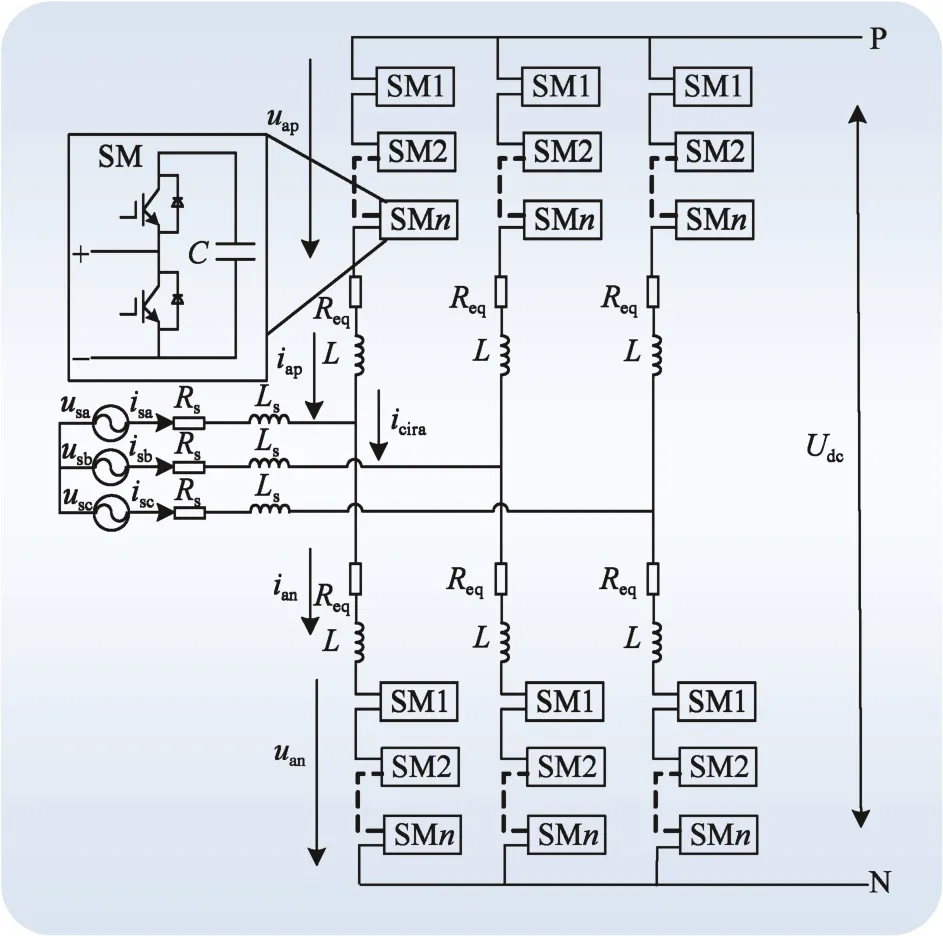
图1 MMC的三相拓扑结构Fig. 1 Three-phase topology of MMC

图1中，子模块SM为典型的单相半桥结构，由2个带有反并联二极管的绝缘栅双极型晶体管（IGBT）和一个直流储能电容C并联组成。通过控制开关管的开通与关断，子模块两端电压在电容电压与零之间进行切换，从而控制子模块在电路中的投入与切除。

由于整流器的3个相单元完全对称，本文以a相为例进行分析。在图1中，uap、uan分别为a相的上、下桥臂的子模块电压之和，iap、ian分别为a相的上、下桥臂电流，isa为交流侧的输入电流，Udc为直流母线电压。

1.2 载波移相调制策略

采用载波移相产生开关信号，其原理为：将n个幅值和频率相同但相位不同的三角载波与同一个正弦调制波进行比较，从而生成脉宽调制（PWM）信号[15]。结合MMC的拓扑结构，要使上、下桥臂投入的子模块数量之和保持为n，则需满足上桥臂投入子模块的数量与下桥臂切除子模块的数量相等。因此，上、下桥臂调制波的相位应该相反。

根据文献[16]，本文采用2n+1电平调制方式。具体实现如下：首先将取反后的参考电压信号作为上桥臂的调制波，将参考电压信号作为下桥臂的调制波。上、下桥臂的三角载波相位的设置因n的奇偶性而不同。当n为奇数时，上、下桥臂的三角载波设置相同，相位都分别相差360°/n；当n为偶数时，上桥臂的载波相位仍然相差360°/n，将上桥臂的载波分别移相180°/n作为下桥臂的载波。

2 电容电压均衡控制策略

在考虑电路参数完全一致的情况下，根据MMC的拓扑结构可知：MMC工作时，各子模块的直流储能电容会不停地进行充、放电，从而使电容电压偏离参考值，产生电容电压的波动。因采用载波移相调制策略，并且开关频率低，三角载波之间的相位差会使各子模块的直流储能电容充、放电的时间有所区别，从而导致各子模块电容电压的不一致。实际电路的参数不可能完全一致，所以电容电压不均衡的问题会更加凸显。因此，需采取合理的方式对电容电压进行均衡控制。

2.1 传统均压控制策略

图2所示为基于载波移相的传统电容电压均衡控制策略。图2中，upj、unj分别为最终得到的上、下桥臂电压调制信号；分别是通过平均电压控制和电压均衡控制得到的电压调制量；是采用电压外环电流内环控制得到的参考电压。

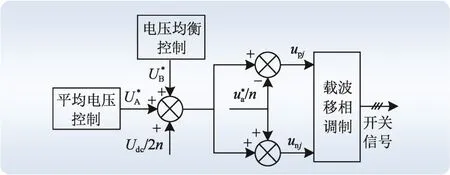
图2 MMC的传统控制策略Fig. 2 Traditional control strategy of MMC

另外，以下所述的控制策略仍然是以 a相为例，j=1,2,···,n。

根据图2，上、下桥臂的调制信号的数学表达式为：

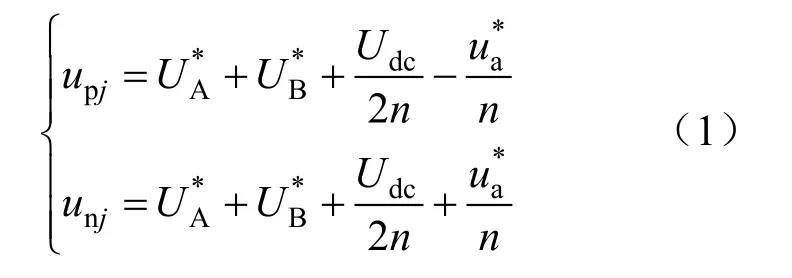
2.2 引入桥臂电容电压平均值前馈

设模块化多电平换流器的调制度为M，交流侧输入相电压的幅值为Usm，则有：

若将三角载波的幅值设为1。根据调制度的幅值定义，上、下桥臂的调制信号的幅值应该和调制度相等。为满足此关系，需要引入一个比例Kc。以上桥臂为例，有

设Ucref为子模块电容电压的参考值，根据MMC的工作原理，则在理想情况下得到的直流输出电压应为

在传统均压策略中，Kc是一个常数。令Kc=Ucref，假设电网电压稳定不变。根据式（3），直流母线电压会随着调制信号的变化而变化，其稳定性会受到子模块电容电压变化的影响。

传统均压策略的核心是让电容电压跟随参考值，从而降低电容电压的波动量；其对电容电压的一致性没有针对性措施。

在能够保证电容电压波动在合理范围内的前提下，本文基于传统策略，研究如何提高电容电压的一致性。

每一相所有子模块电容电压平均值的变化可以表征子模块电容电压的变化。将子模块电容电压的变化看作为一个扰动量。设Ucava为a相所有子模块电容电压的平均值，令Kc=Ucava。当电容电压发生变化时，调制信号也随之发生变化。根据式（3），模块整体电容电压变化对直流母线电压的影响会非常小，可近似认为直流母线电压不受子模块电容电压变化的影响。同时，调制信号跟随平均值变化，调制后得到的子模块电容电压会更加接近它们的平均值，使电容电压的一致性变好。

将上述改进策略称之为桥臂电容电压平均值前馈控制。令Uapj、Uanj分别为上、下桥臂每个子模块的电容电压，则上、下桥臂各子模块电容电压的平均值计算公式为：

a相所有子模块电容电压的平均值的表达式为：

将图2得到的上、下桥臂调制信号分别除以实时的电容电压平均值，得到新的上、下桥臂调制信号，其数学表达式为：

图3所示为引入桥臂电容电压平均值前馈的改进均压策略。

图3 桥臂电容电压平均值前馈控制Fig. 3 Bridge arm capacitor voltage average feedforward control

2.2.1 相单元平均电压控制

相单元平均电压控制的目的，是使所有子模块电容电压的平均值能够跟随其参考值，从而实现各子模块电容能量的均匀分配，具体控制如图4所示。

图4 相单元平均电压控制Fig. 4 Phase cell average voltage control

环流控制器为PI控制器，其通过参考电压进行反馈控制，使由上、下桥臂电流得到的环流实际值跟随由电压外环得到的环流参考值。

2.2.2 桥臂子模块电容电压均衡控制

桥臂子模块电容电压均衡控制的目的，是使所有子模块电容电压都跟随给定的电压参考值，从而降低电容电压的波动。具体控制如图5所示。

图5 桥臂子模块电容电压均衡控制Fig. 5 Bridge arm sub-module capacitor voltage equalization control

在图5中，Uapj、Uanj分别为a相上、下桥臂的所有子模块电容电压，K为比例系数。上、下桥臂参考电压的极性是由各自桥臂电流的正负决定的。具体实现如下：

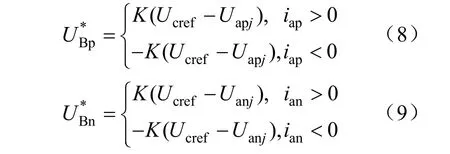
2.3 均压效果的衡量指标

电容电压均衡的目的，一方面是为了降低电容电压的波动，另一方面是使各个子模块的电容电压有良好的一致性。因此，用电容电压波动率和电容电压离散度这2个指标来衡量电容电压均衡策略的效果[17]。

电容电压波动率为各个子模块电容电压和电容电压参考值之间的最大差值与电容电压参考值的比值。电容电压波动率ε的计算表达式为：

式中：uc(t,j)为t时刻第j个子模块的电容电压。

电容电压离散度为各个子模块电容电压之间的最大差值与电容电压参考值的比值。电容电压离散度σ的计算表达式为：

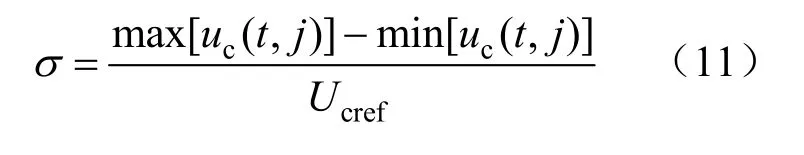
3 仿真实验

为了验证上述改进策略的有效性，在MATLAB/SIMULINK中搭建了 17电平模块化多电平整流器的仿真模型。

该整流器模型是 10 kV/380 V配电网下的MMC型电力电子变压器的输入级，具体的仿真模型参数设置如表1所示。

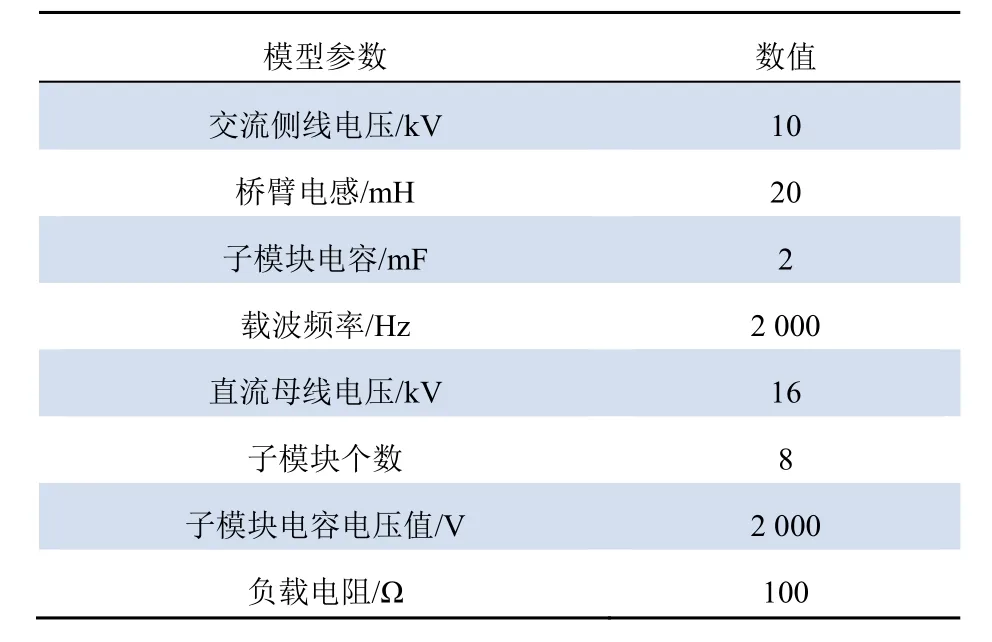
表1 仿真模型参数Tab. 1 Simulation model parameters

3.1 稳态对比分析

分别采用传统的电压均衡控制策略和改进的电压均衡控制策略进行仿真。子模块电容电压的仿真结果如图6和图7所示。

图6 传统电压均衡控制策略仿真结果Fig. 6 Simulation results of traditional voltage balance control strategy

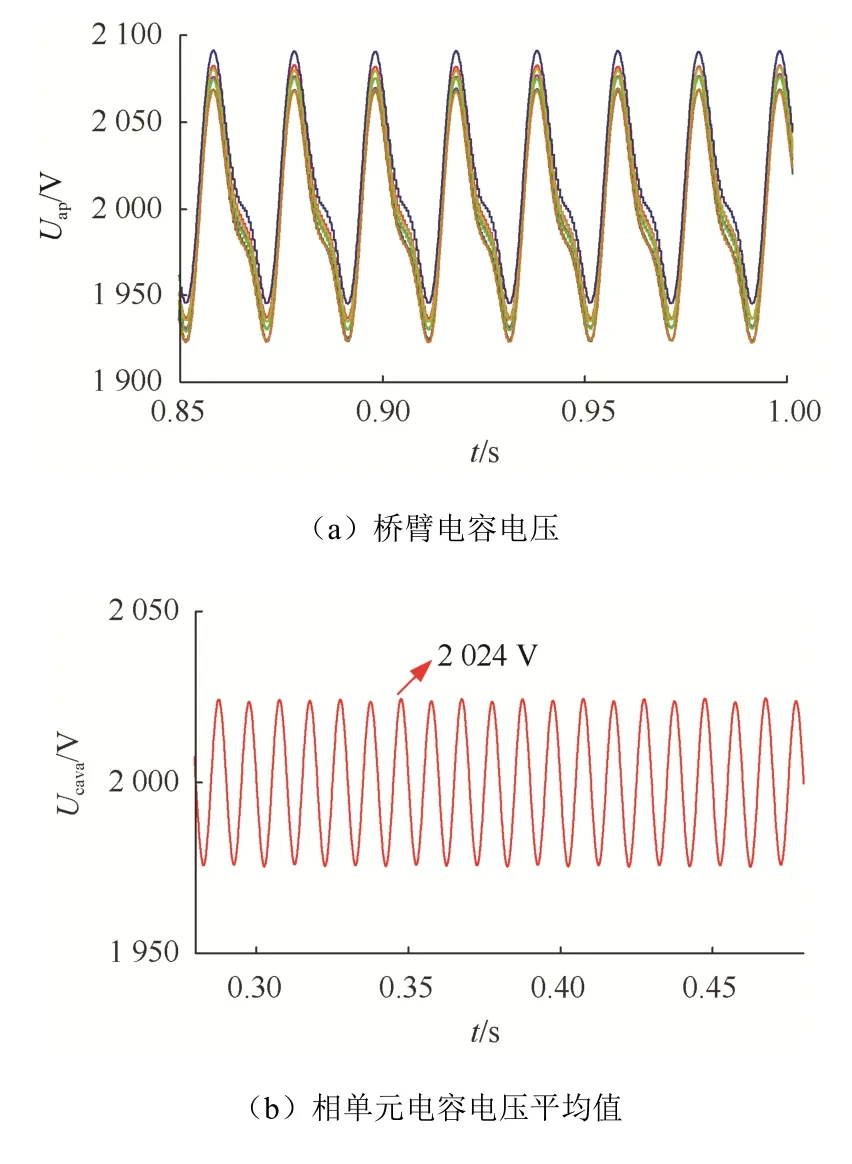
图7 改进电压均衡控制策略仿真结果Fig. 7 Simulation results of improved voltage balance control strategy

图6（a）与图7（a）为a相上桥臂8个子模块电容电压的变化曲线。应用仿真软件里的测量工具测得：在传统电压均衡控制策略下，子模块电容电压与参考值之间的最大差值为80 V，8个子模块电容电压之间的最大差值为35 V；在改进电压均衡控制策略下，子模块电容电压与参考值之间的最大差值为91 V，8个子模块电容电压之间的最大差值为23 V。表2所示为2种控制策略下电容电压波动率和离散度的对比结果。

表2 2种策略下电容电压波动率和离散度的对比Tab. 2 Comparison of capacitance voltage fluctuation and dispersion under two strategies%

从表2可以看出，与传统电压均衡控制策略相比：改进电压均衡控制策略的电容电压波动率有所增加，但数值仍在5%以下；电容电压离散度减小。根据上述分析，可以得出结论：改进电压均衡控制策略使电容电压的一致性更好，虽然增大了波动，但并未超过合理的波动范围。

图6（b）与图7（b）为a相所有子模块电容电压的平均值的变化。从图中可以看出，2种策略下的电容电压平均值变化一致。

图8示出了2种策略下输出直流侧母线电压的变化对比曲线。可以看出，改进策略下，稳定后的波形明显要比传统策略稳定后的波形波动幅度小。这说明，改进的电压均衡控制策略可以使MMC更好地维持直流母线电压稳定在给定值，从而为下一级提供了更稳定的直流电压。

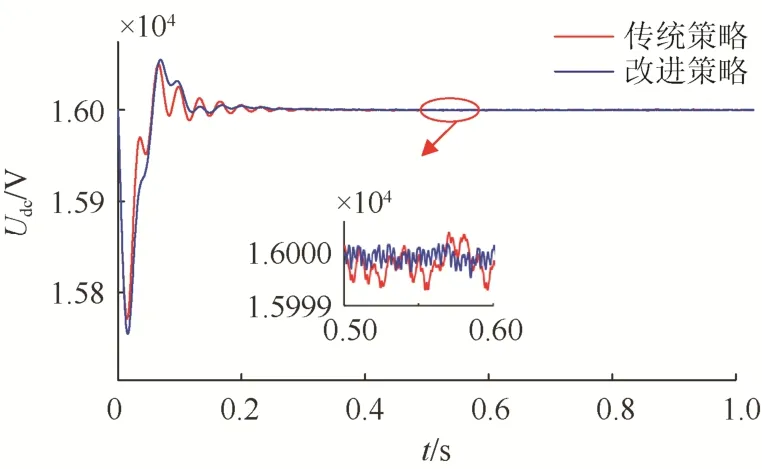
图8 2种策略下直流母线电压的对比Fig. 8 Comparison of DC bus voltage under two strategies

图9为2种策略下a相上桥臂的桥臂电流的对比曲线。从图9中可以看出，改进电压均衡控制策略下的桥臂电流波形明显要比传统策略的波形更接近正弦波。利用傅里叶分析工具，可以得到：传统策略下的桥臂电流的谐波畸变率为 14.26%，而改进策略下的桥臂电流的谐波畸变率为11.46%。

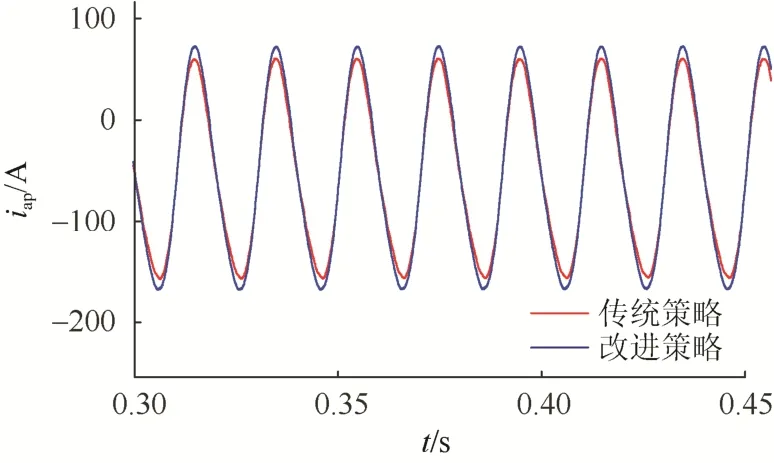
图9 2种策略下a相上桥臂电流的对比Fig. 9 Comparison of bridge arm current in phrase A under two strategies

3.2 动态仿真实验

为了验证改进电压均衡控制策略的暂态稳定能力，在0.2 s时将负载由100 Ω变为50 Ω。

传统策略和改进均压控制策略下的子模块电容电压波形变化如图10所示。

图10 负载突变时的电容电压波形变化Fig. 10 The capacitance voltage waveform changes when the load changes abruptly

从图10可以看出：在0.2 s之后，2种策略下子模块电容电压的波动幅值都迅速增加。但是，传统策略下电容电压达到稳定需要的时间较长，约0.7 s；而改进策略下电容电压在0.4 s时就可以达到稳定。

由此可以得出：负载突变时，改进策略下电容电压的稳定性比传统策略更好。

4 结论

本文在基于载波移相调制的传统电容电压均衡控制策略的基础上，提出了引入桥臂电容电压平均值前馈的改进均压策略。通过仿真实验，得到以下结论。

（1）与传统电容电压均衡控制策略相比，本文引入桥臂电容电压平均值前馈，可使子模块电容电压在合理的波动范围内获得更好的一致性，从而使直流母线电压在给定值附近的波动更小。

（2）在暂态稳定的验证中，突降负载后，本文提出的改进均衡控制策略能够使系统更快达到稳定。

本文策略可以应用到中压配电网下的模块化多电平电力电子变压器的输入级。