基于改进Quasi-Z源逆变器的VSG光伏并网模型预测控制

熊军华，郑炳校，王亭岭，陈逸峰，赵 君

（华北水利水电大学 电力学院，河南 郑州 450045）

0 引言

在新能源利用中，光伏发电具有很好的发展前景。我国西部地区光能资源丰富，光伏发电对促进西部经济发展具有重要意义[1]。

传统光伏发电逆变器前级需要额外增加DC/DC变流器，这既加大了系统的控制难度又带来了经济成本问题。此外，为了防止逆变器同一桥臂上下管直通，其脉宽调制（PWM）需要插入死区；然而死区的注入将引起谐波量输出大、电流波形畸变等死区效应，容易致使系统电磁兼容性变差。

Z源逆变器（Z-source inverter，ZSI）自带升降电压变换功能[2]，允许同一桥臂上下导通，可以克服传统逆变器固有的局限性；但其存在输入端电流不连续、电容两端电压应力高、大功率场合升压能力受限制等缺陷。

为了克服这些缺陷，文献[3,4]通过增加器件提高了ZSI升压能力，但器件的增多也带来了控制难度与经济成本的问题。文献[5-7]提出了Quasi-Z源T型拓扑逆变器。该设备特点是输出谐波含量低、有利于减小输出滤波器体积及成本；但在用于高压场合时，其功率管承受电压应力大。文献[8-10]提出了新型准 Z源三电平逆变器拓扑结构。相比传统结构，其优点是提高了逆变器升压能力并减小了电容电压应力；但其升压范围仍受升压比限制，导致升压调制不灵活。

随着分布式发电系统装机容量的增加以及同步发电机装机容量的减少，电力系统具备的转动惯量和旋转备用容量因变小而已经难以为电网提供足够的惯性和阻尼支撑，这将给电网安全稳定运行带来隐患[11,12]。VSG模拟了传统同步发电机（synchronous generator，SG）工作原理，具备一定的惯性和阻尼特性。传统 VSG控制分为电流型[13]和电压型[14]。电流型VSG控制适用于惯性和阻尼大的电网环境下的并网运行模式；电压型则适用于分布式电源渗透率高的环境或孤岛运行模式。

针对实际电网电压跌落、不平衡或波形畸变等故障问题，文献[15]将有功、无功功率的平均值作为VSG的正序参考指令值，电网电压前馈函数值作为平衡系数，降低了故障电压的干扰并实现了三相并网电流的输出平衡；但有功功率、无功功率存在 2倍工频处波动且振幅大。文献[16,17]利用准比例谐振控制器产生的负序电压抑制不平衡电流负序分量，达到了平衡控制目标；但准谐振控制器整定参数较多且复杂，当负载引起的频率变化不在其谐振控制器范围内时会导致系统控制效果差。文献[18]在电流内环参考指令生成环节引入2倍工频的谐振滤波器对负序分量进行抑制，实现了并网电流平衡输出；但谐振滤波器存在频率适应性能较差的缺点，同时还存在因带宽减小而导致系统动态响应变慢的问题。

本文首先建立改进Quasi-Z源NPC型模型，算出Quasi-Z源网络电感负载电流和电容电压的离散时间测量值。然后，推导出三相电压工况不平衡时的改进VSG控制算法，建立离散时间电流指令值。最后，根据Quasi-Z源网络的各离散时间测量值和电流指令值构造基于有限控制集模型预测（finite control set-model predictive control，FCS-MPC）的最优代价函数；无需PWM调制器[19,20]，通过选取最优代价函数值即可输出脉冲控制信号。

1 改进Quasi-Z源NPC逆变器

1.1 Quasi-Z源NPC逆变器拓扑结构

三相Quasi-Z源NPC型逆变器系统主电路如图1（a）所示。逆变器交流侧输出端等效滤波电感为L，等效电阻为R；直流侧由光伏板PV、滤波电容C0以及 Quasi-Z源网络组成。在Quasi-Z源网络中，作为蓄能和滤波的电感有L1=L3、L2=L4；储能电容有C2=C3、C1=C4。

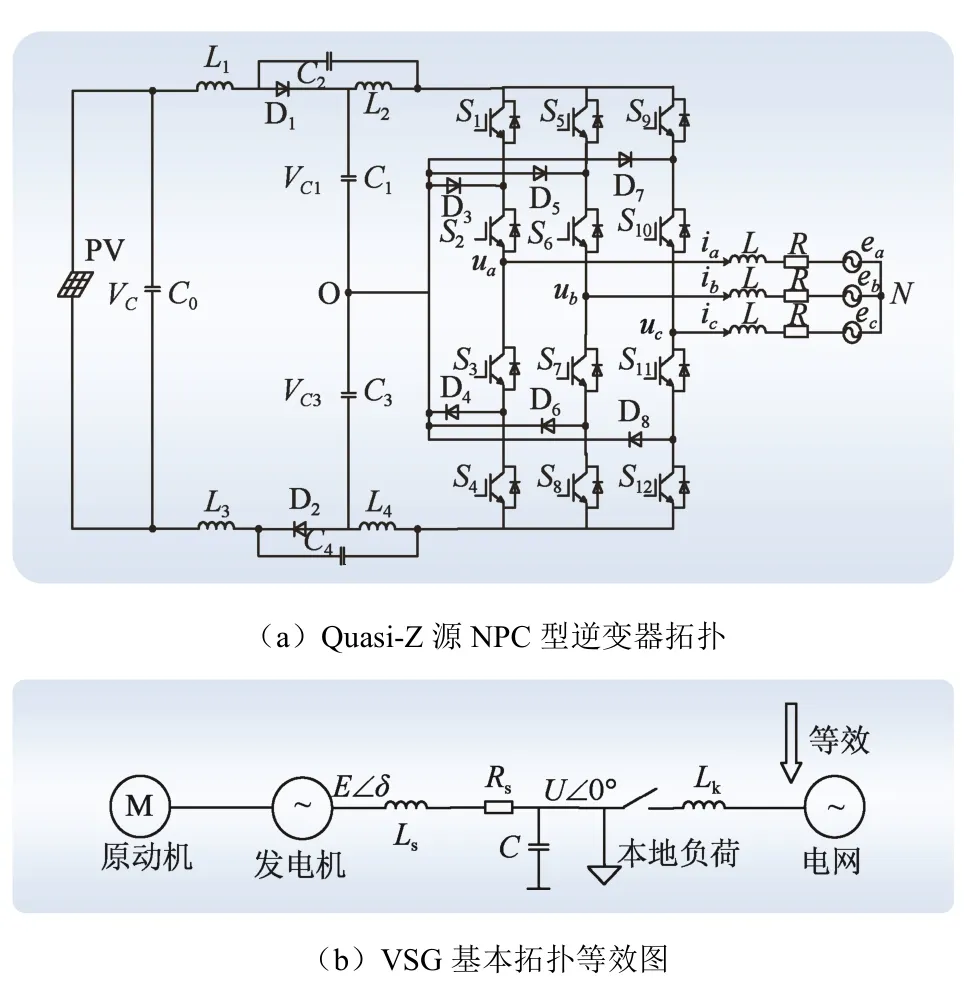
图1 光伏逆变系统Fig. 1 Photovoltaic inverter system

本文采用了改进型VSG控制技术。与传统同步发电机构造模型对应来看，光伏板电压源 PV与 Quasi-Z源网络可看作虚拟的原动机，逆变桥输出电压uo=[uaubuc]T、电流io=[iaibic]T分别等效VSG定子输出端电压和并网电流，L和R等效虚拟同步电感和定子电枢电阻[21]。图1（a）可以通过图1（b）等效表示。

1.2 Quasi-Z源NPC逆变器交流侧数学模型

传统电压源 NPC型逆变器输出电压共有 27种开关状态。为了提高控制效率、除去冗余状态，简化后的Quasi-Z源NPC型逆变器有26种开关组合状态[21]。将 26种开关状态按一定条件交替导通，便可使系统实现升压和逆变。

逆变输出电压可表达为：

式中：a= e-j2π3，将其代入式（1），可得：

式中：x∊[0, 25]；Sa、Sb、Sc分别为各相桥臂的开关状态。从图1（a）可得滤波电感电流方程式为：

1.3 Quasi-Z源NPC逆变器直流侧数学模型

Quasi-Z源NPC型运行状态分为直通状态和非直通状态，等效图如图2所示。图2中，RL、RC分别是电感和电容的寄生电阻，ZL是负载。

图2 Quasi-Z源NPC等效电路Fig. 2 Quasi-Z source NPC equivalent circuit

如图2（a）所示，电路工作在全直通状态。由于图1（a）中的二极管D1、D2截止，此时电容C1～C4释放能量，其释放的能量与电压源一起向电感L1～L4充电。

如图2（b）所示，电路工作于非直通状态。二极管D1、D2导通，电感释放能量。电感和电压源同时向负载提供能量，且部分能量向各电容转移，从而实现升压功能。根据电路图对称性，存在以下关系：

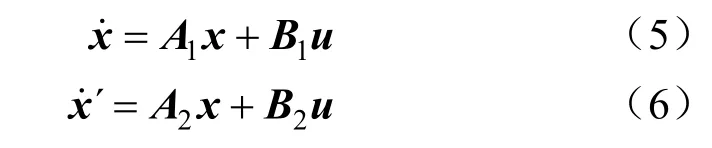
式中：

2 VSG的控制策略

2.1 VSG基本原理

VSG分布式逆变器通过模拟SG输出特性，从而使其运行于并网或离网、具有有功–频率调节和无功–电压调节特性。

当分布式逆变器并入强电网工作时，受高压电网特性影响，逆变器输出电压幅值及频率均被钳位。此时，模拟 SG调频器的下垂特性环节和励磁器的端电压下垂调节环节失效。在强电网下，VSG逆变器表现的转子运动机械特性及无功功率–电压幅值特性如式（7）～（9）所示。

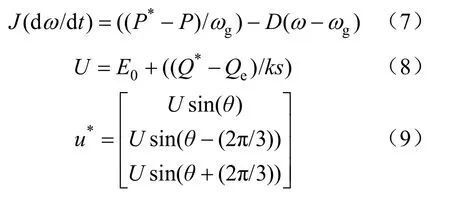
式中：ω为VSG电角度速度，rad/s；ωg为电网同步电角速度(设发电机极对数为1)，rad/s；J为VSG的转子转动惯量，kg·m²；D为VSG的阻尼系数，N·m·s/rad；P*、Q*分别为有功功率、无功功率参考值；k为无功功率调节系数；E0为空载电势；θ为VSG的电角度；U为VSG内电势输出幅值指令；u*为逆变器输出参考电压值。图3是VSG的控制框图。

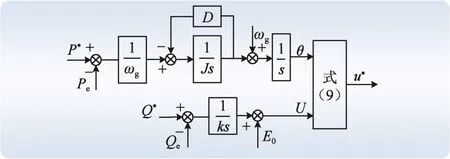
图3 VSG的控制框图Fig. 3 Control block diagram of VSG

2.2 VSG外环输出电流指令计算

在三相电网电压不平衡工况下，输出指令电压u*将包含负序电压分量。为了抑制负序电压分量，同时忽略逆变器交流侧滤波电容支路作用，采用dq坐标系分解。正序电压、电流之间的关系为：

为了便于计算和控制，忽略二阶微分部分，VSG控制电流指令框图如图4所示。

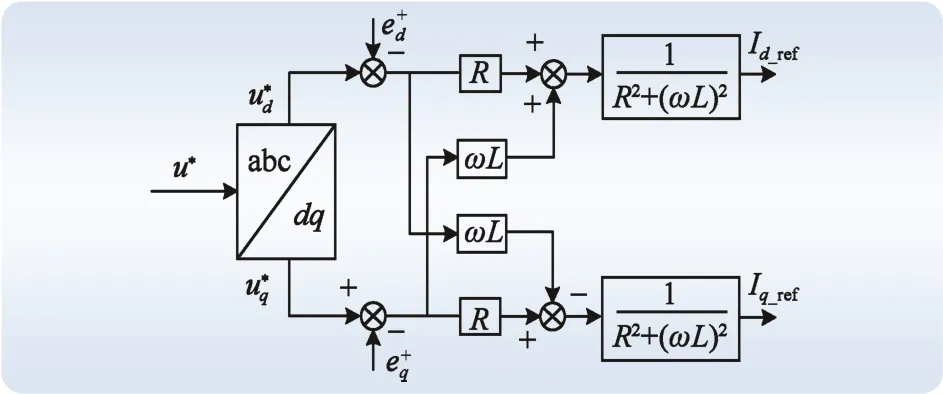
图4 VSG外环控制电流指令Fig. 4 VSG outer-loop current command control

2.3 不平衡电网下改进VSG控制策略

当电网负载发生不平衡时，忽略电压电流高次谐波分量，逆变器输出瞬时有功功率和无功功率可表示为：

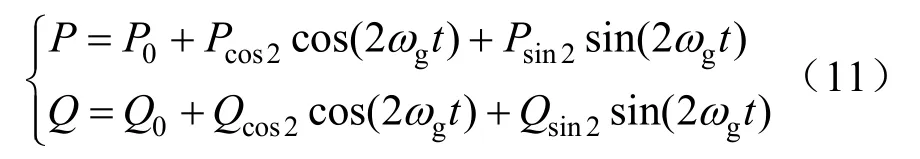
式中：P0、Q0分别为瞬时平均有功、无功功率；Pcos2、Psin2分别为余弦有功、正弦有功2倍工频交流功率；Qcos2、Qsin2分别为余弦无功、正弦无功2倍工频交流功率。

同时，有：

式中：上标“+”、下标“－”分别表示正序、负序分量；下标“dp”、“qp”分别表示正向同步旋转dq轴坐标系分量；下标“dn”、“qn”分别表示负向同步旋转dq轴坐标系分量。

从式（11）可以看出，有功功率、无功功率出现2倍工频波动主要由负序电压、电流分量引起。在不平衡三相电压工况下，为了使逆变器输出电流平衡并减少有功或无功功率波动，可以以正序电流作为参考值实现不同的改进控制目标。

（1）不平衡三相电压下，实现逆变器输出三相电流平衡，即抑制负序分量的出现并设置为0。将式(12)的电压正序分量值固定在正向同步旋转坐标系d+轴上，则。结合式（9）～（12），通过计算化简可得：

式中：上标“*”表示各控制量的目标指令值。

（2）消除输出有功功率 2倍工频波动，即Pcos2=Psin2=0，经化简可得：

式中：kdd、kqd为电网电压不平衡的调整参数；。

（3）消除输出无功功率 2倍工频波动，即Qcos2=Qsin2=0，经化简可得：

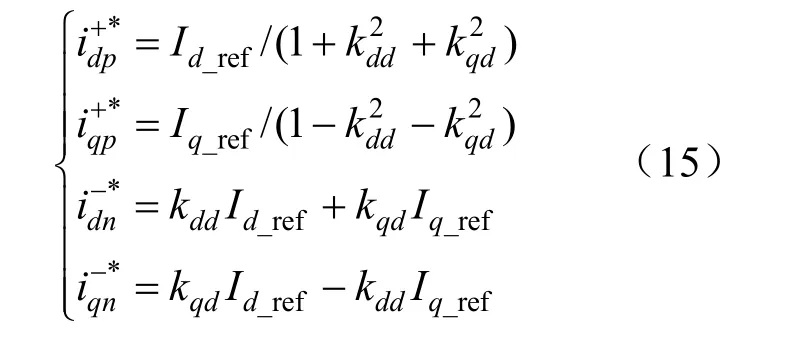
3 系统模型预测控制

对于 Quasi-Z源拓扑的传统逆变器，采用PWM控制其升压范围会受限于占空比D和调制度M，且D和M又存在相互制约关系。

采用 FCS-MPC，能省略内环 PI环节，使控制过程不受调制度M和占空比D制约，从而提高了控制系统的灵活性及升压范围[22]。

实现系统的FCS-MPC策略，需要建立系统各状态变量的离散模型。设信号采样周期时间为Ts，使用欧拉前向差分公式将式（3）离散化为两相静止坐标系下的式（16）。

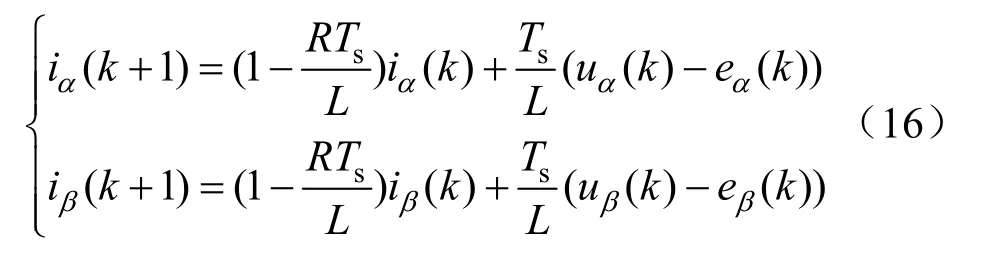
式中：负载电流iα、β(k)、iα、β(k+1)分别为第k时刻的采样值、第k+1时刻的预测值；uα、β(k)为第k时刻的采样值；eα、β(k)为电网电压第k时刻的采样值。

同理，忽略Quasi-Z网络电感和电容的寄生内阻，将式（5）离散化，可得直通状态离散化式（17）。

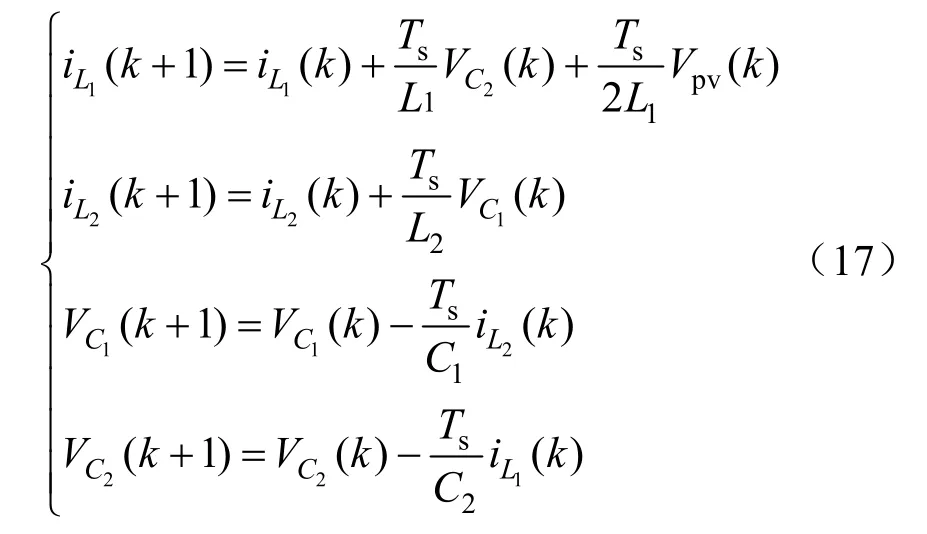
式中：VC1(k)、VC2(k)、Vpv(k)分别为电容C1电压、电容C2电压、光电池电压的第k时刻采样值；VC1(k+1)、VC2(k+ 1 )分别为电容C1电压、电容C2电压的第k+1时刻预测值；iL1(k)、iL1(k+ 1 )分别为蓄能电感L1的第k时刻采样值以及第k+1时刻的预测值；iL2(k)、iL2(k+ 1)分别为蓄能电感L2的第k时刻采样值以及第k+1时刻的预测值。

将式（6）离散化，可得非直通状态离散化式（18）。

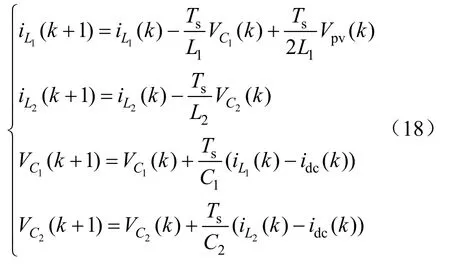
式中：idc(k)=Sa(k)ia(k)+Sb(k)ib(k)+Sc(k)ic(k)；Sa、Sb、Sc为开关状态。

图5是FCS-MPC算法流程图。图5中，g(x)、gopt、xopt、x为变量参数。

图5 FCS-MPC算法流程图Fig. 5 FCS-MPC algorithm flow chart

首先，测量Quasi-Z源网络的相关电感电流、电容电压和交流侧电压、电流各个第k个周期实际值，算出光伏MPPT控制模块和改进VSG控制模块分别产生的参考信号。

然后，由式（16）（17）（18）预测第k+1周期相关电感电流、电容电压值。

最后，将第k+1周期的预测值与参考值代入代价函数g，算出最优开关组合。

代价函数为：

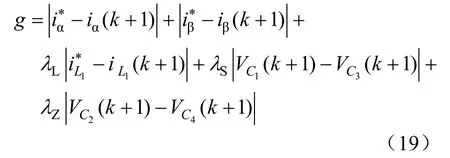
式中：λL、λS、λZ为权重系数。

4 仿真分析

为了验证上述系统结构及控制策略，利用MATLAB/SIMULINK搭建了如图 6所示的总体仿真结构。图6中，Quasi-Z源网络主要参数：C1、C2、C3、C4取值为 2 200 μF；L1、L2、L3、L4、取值为 5 mH，电感、电容寄生等效电阻均取值为10 mΩ，Vpv直流输入电压为350 V。控制参数J取0.3 kg·m²，D取12 N·m·s/rad，Ts取30 μs，λL取 0.73、λS取 0.45、λZ取 0.26。

图6 系统总体控制框图Fig. 6 System overall control block diagram

4.1 改进Quasi-Z源NPC型性能验证

计算条件：在电网正常工况下，给定改进型Quasi-Z源NPC型逆变器和传统型逆变器同等条件。设系统有功功率P=10 kW、无功功率Q=0 var。

图7（a）为基于FCS-MPC方法的输出电流波形，图7（b）为基于SVPWM控制的输出电流波形。

图7 逆变器交流侧负载输出Fig. 7 Inverter AC side load output

通过比对可以发现，图 7（a）的波形比图 7（b）更光滑、高次谐波少。这说明，由SVPWM控制的输出波形质量比 FCS-MPC控制的输出波形质量差。由于SVPWM控制的输出波形叠加高次谐波多，不光滑，容易产生电磁干扰，这间接说明FCS-MPC策略运用于Quasi-Z源NPC拓扑型上更具有优势。

图8示出了基于改进型Quasi-Z源NPC型逆变器和传统逆变器并网输出电流总谐波畸变率（total harmonic distortion，THD）。图9所示为改进型Quasi-Z源NPC型逆变器交流侧线电压输出波形。图10所示为A相输出的电压、电流波形。

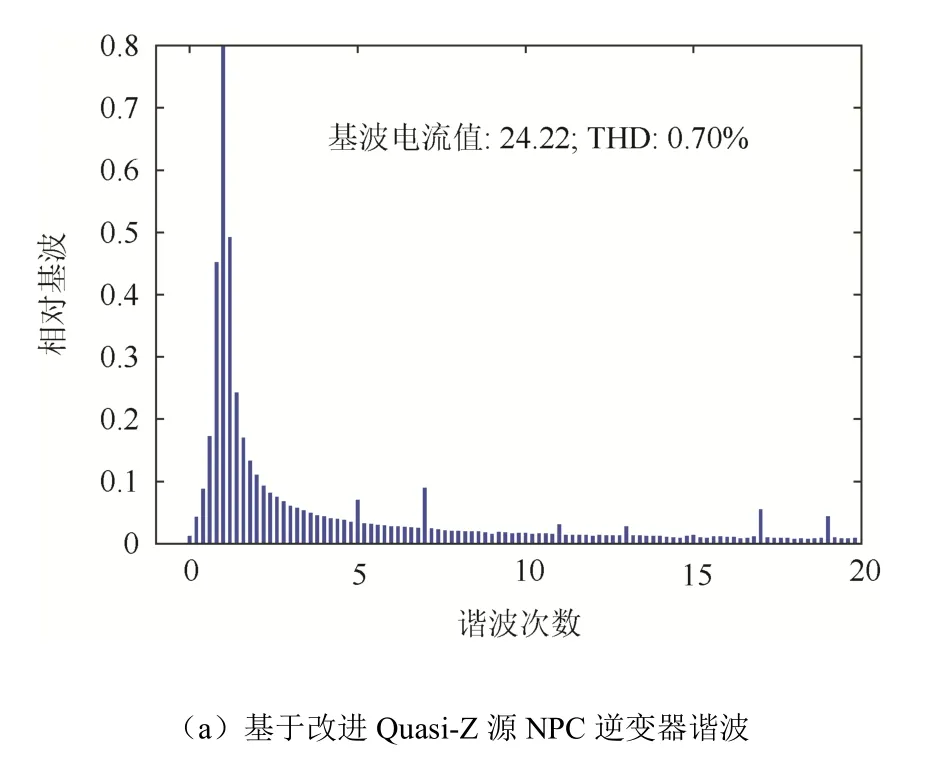
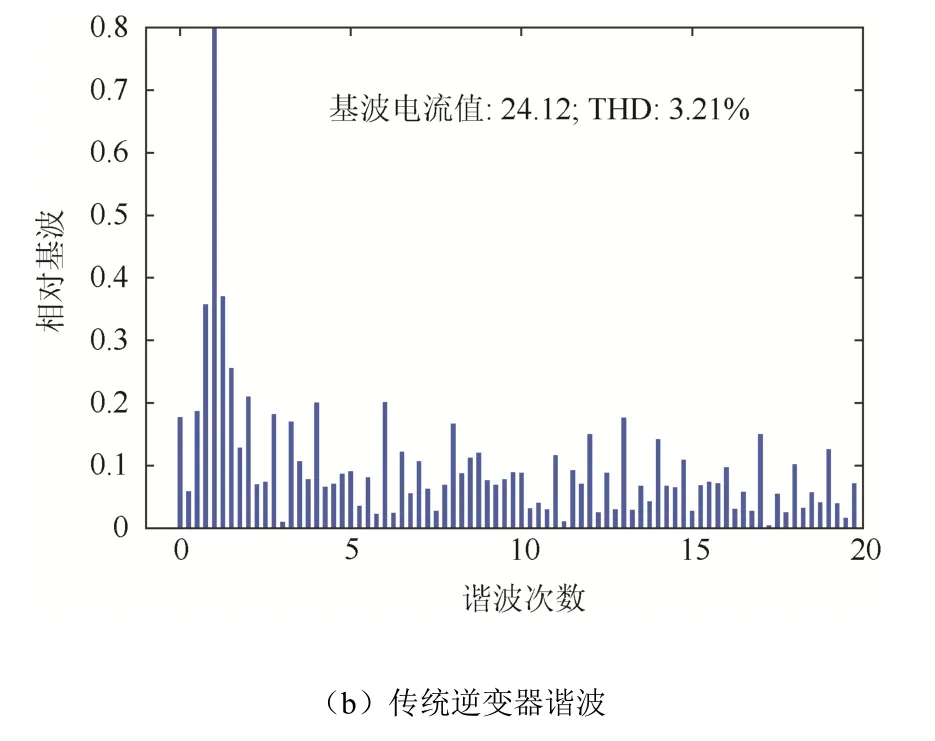
图8 总谐波畸变分析Fig. 8 Total harmonic distortion analysis

图9 交流侧输出线电压Fig. 9 Voltage value of AC side output line

图10 A相电网电压和电流变化Fig. 10 Voltage and current variation of phase A grid

图8（a）的并网电流 THD比图 8（b）低2.51%。图8（a）中THD的减少以及图9交流侧输出波形的良好，有助于滤波器滤除高次谐波，同时有利于减小滤波器体积，节约经济成本。图10中，电压和电流同频同相，这说明功率因数的提高可以减小线路损耗。

4.2 改进VSG控制策略验证实验

计算条件：给定电网有功功率P=10 kW，无功功率Q=9 kvar。将电网电压A相幅值降低到原来一半，B相减低为原来的80%。仿真总时长为2 s。

不平衡电压如图11（a）所示：0～0.5 s为正常电压，0.5 s ～1 s为不平衡电压，1 s后恢复正常。图11（b）所示为采用改进VSG不平衡控制策略输出电流：最大电流幅值为42.1 A，最小电流幅值为41.2 A，不平衡度为1.3%。图11（c）所示为传统VSG控制策略输出电流：最大电流幅值为44.5 A，最小电流幅值为 33.6 A，不平衡度为16.6%。

图11 VSG不平衡电压输出电流Fig. 11 VSG unbalanced voltage output current

在三相电压不平衡度减轻情况下，采用传统VSG控制策略和改进 VSG控制策略输出电流效果大致相同（仿真图略）。

由此可知，在发生严重的三相电网电压不平衡时，本文改进VSG不平衡控制策略比传统VSG控制质量更佳。

为了验证在三相电网电压不平衡工况时，本文策略对输出有功功率P、无功功率Q输出波形的控制效果，进行如下仿真计算：设仿真总时长为2 s，在0.5 s～1 s和1.2 s～1.5 s时，将A相电压幅值降低为原来的 50%、B相降低为原来电压60%，其余时间为正常状态。

图12（a）和图12（b）分别示出了改进VSG不平衡控制策略下的有功和无功输出功率曲线。与图12（c）和图12（d）所示的传统VSG不平衡策略控制结果相对比：

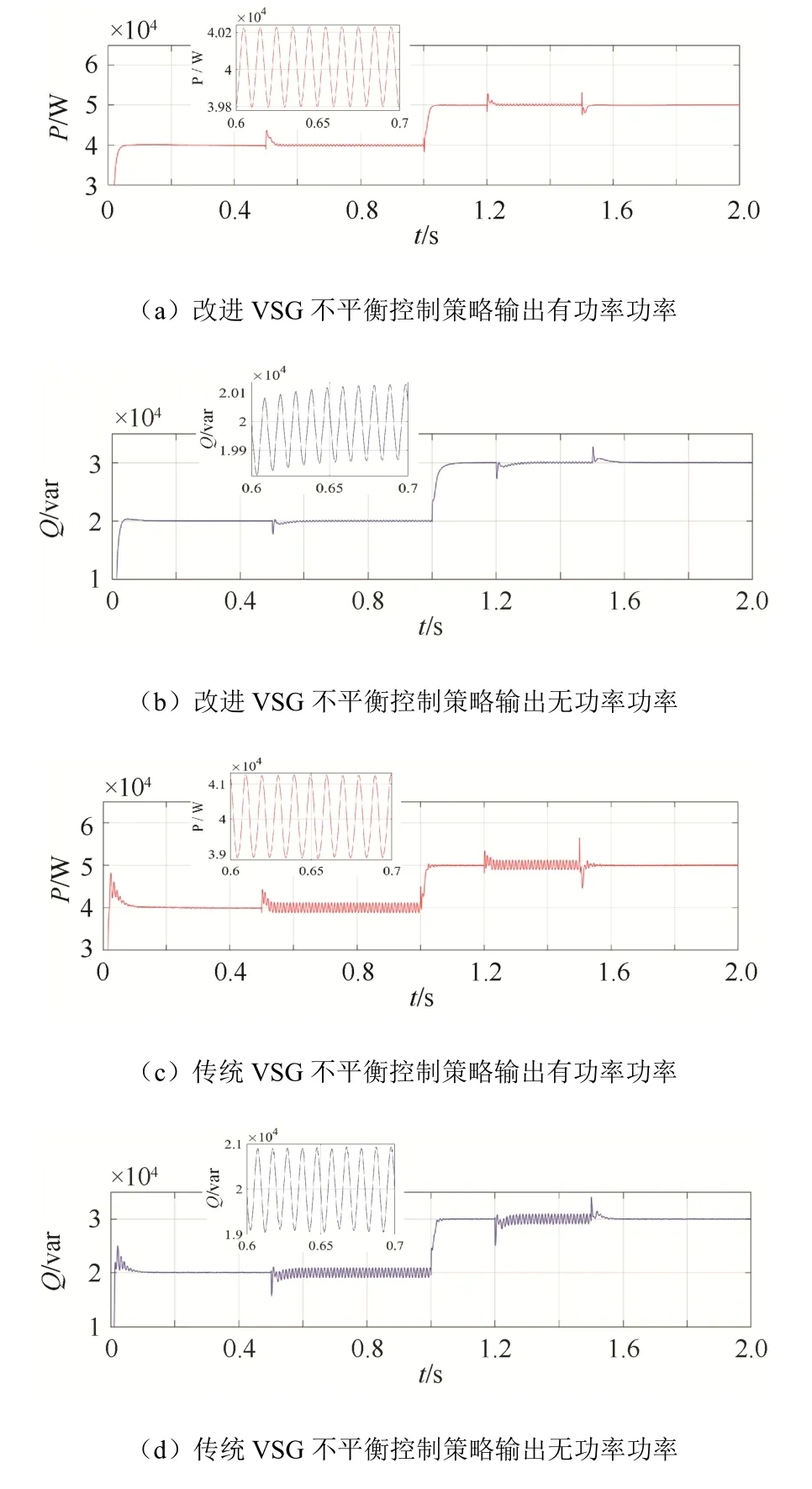
图12 VSG控制策略输出功率Fig. 12 Power output of VSG control strategy

在0.5 s～1 s和1.2 s～1.5 s时段，当三相电网电压不平衡时，改进VSG不平衡控制策略的输出有功功率、无功功率的峰–峰值分别为0.4 kW和0.3 kvar，而传统VSG控制策略分别为2 kW和1.9 kvar。这说明，当电网发生不平衡工况时，改进VSG不平衡控制策略在抑制功率幅度振荡方面更有优势。

在1 s～2 s时段，有功功率从P=40 kW跳跃至P=50 kW，无功功率从Q=20 kvar跳跃至Q=30 kvar。可以看出，改进后的控制策略拥有跟踪电网功率突变的能力，这表明：改进后的VSG控制策略仍具有传统VSG控制策略的动态、静态运行特性。

5 结论

本文在基于传统 VSG不平衡控制策略基础上，提出了改进VSG不平衡控制方法：在电路拓扑上，将传统拓扑型逆变器替换为改进 Quasi-Z源 NPC型拓扑型逆变器；在控制系统上，使用FCS-MPC替代传统PI和PWM控制器。

仿真验证实验结果表明，上述策略具有可行性，具体结论如下。

（1）改进Quasi-Z源NPC型拓扑型逆变器有如下优点：有利于减少THD，并提高逆变器输出负载电流波形质量，可减少对电网的污染；有利于减小交流侧滤波器体积，节约经济成本。

（2）当三相电网电压发生不平衡工况时，使用改进VSG不平衡控制策略的逆变器，可实现三相并网电流平衡输出，对输出有功、无功功率2倍工频振荡的抑制比传统控制方式效果更明显，有利于电网稳定运行。

（3）使用FCS-MPC有利于简化系统参数的复杂程度、减少非线性参数之间的耦合、提高系统的响应度，使调制更加灵活。

（4）在忽略高次谐波影响前提下，不管是改进VSG还是传统VSG不平衡控制策略，在三相电网不平衡工况，由于负序电压和正序电流相互作用，在逆变器输出的有功、无功功率中仍然存在2倍电网工频成分，功率振荡仍然存在。