交直流配电网可靠性和经济性评估及配置优化

2022-08-31苏海锋武泽君王天瑞

电力科学与工程 2022年8期

苏海锋，武泽君，赵岩，王天瑞

（华北电力大学电气与电子工程学院，河北保定 071003）

0 引言

随着配电网中直流负荷比例和分布式电源数量的不断增加，以及用户对供电可靠性要求的提高，配电网供电能力和供电可靠性也需要得到进一步加强。但是现阶段，增设交流配电网网架已经很困难。在同等线路条件下，直流配电网在传输电能时比交流配电网的线路损耗更小、供电半径更大、电压波动更小、电能质量更优秀[1]。所以，交流配电网直流化成为配电网发展的主要方向。

受当前电力电子器件发展技术水平的影响，直流设备在运行中仍然存在故障率高和成本高的问题。所以，在进行交流配电网直流化改造时，应当考虑混合交直流配电网设备的配置优化，以便综合提升混合交直流配电网的可靠性与经济性。

文献[2]对直流配电网的特点进行了介绍，简略分析了其拓扑和电压等级。文献[3]分析了两端和三端交直流结构的供电能力。文献[4]分析了不同渗透率下直流配电网的供电能力。以停电时间不同划分负荷，文献[5]考虑了电压源换流器控制模式。文献[6]考虑了直流变压器配置，但是考虑的设备数量少且网络结构较为简单，其方法不适合对负荷较多的混合交直流配电网进行分析。文献[7,8]对现阶段直流设备的可靠性进行了分析，对比了交、直流配电网的可靠性；但是文中并未考虑负荷类型及分布式电源（distributed generation，DG）的影响。文献[9]考虑设备制造水平和直流电压等级的主要约束条件，提出了高、中、低压的直流配电网电压等级序列，但是并没有对低压直流等级进行验证。文献[10]在混合模块化多电平换流器（modular multilevel converter，MMC）可靠性计算的基础上，讨论了MMC的直流故障穿越能力。以上文献在一定程度上推进了对直流配电网供电能力和设备可靠性的研究，但是对于关键设备可靠性、不同负荷停电成本、不同设备配置下混合交直流配电网的可靠性和经济性的考虑较少。

针对以上问题，本文首先提出混合交直流配电网的可靠性和经济性指标；然后以MMC、直流断路器（DC circuit breaker，DCCB）、线路、换流站、变压器的成本和停电成本之和作为经济性目标函数，分析设备本身的可靠性；最后使用改进狼群算法优化设备配置，用蒙特卡洛法计算得到评估结果。

1 综合评估指标及模型

1.1 建立综合指标体系

考虑经济性和可靠性，建立混合交直流配电网的评估体系如图1所示。

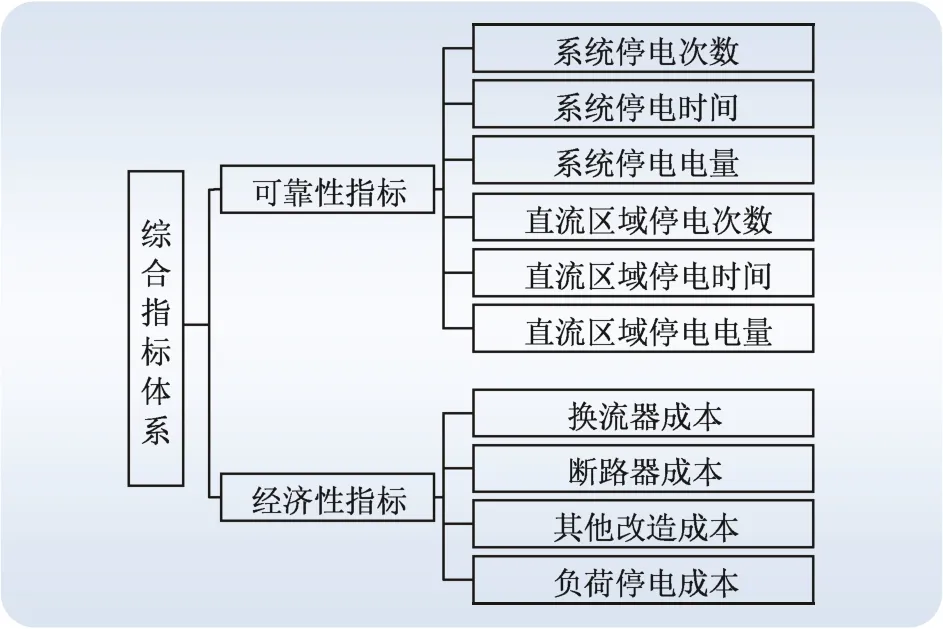
图1 综合指标体系Fig. 1 Comprehensive index system

1.2 单相指标及量化

1.2.1 直流可靠性指标

传统的可靠性指标包含系统停电频率（SAIFI）、系统停电时间（SAIDI）、系统停电电量（ENS）等。

混合交直流配电网包含交流和直流2部分。为使评估更加完善，其可靠性以交、直流性质分别计算。

直流负荷停电频率（dc SAIFI，DCSAIFI）：

式中：M为受到停电影响的直流区域数；N为总的直流区域数；λi,DC为停电影响范围内的第i个直流负荷点的停电次数；Ni,DC为第i个直流负荷点的直流负荷数。分子表示受停电影响范围内直流负荷数，分母为总直流负荷数。

直流负荷停电时间（dc SAIDI，DCSAIDI）：

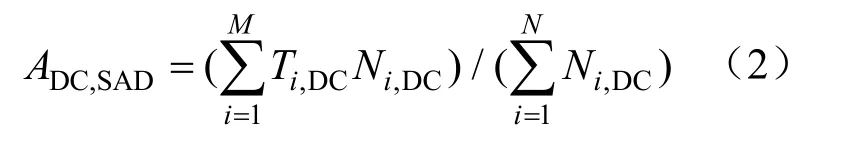
式中：Ti,DC为停电影响范围内的第i个直流负荷点停电时间；Ni,DC为第i个直流负荷点的直流负荷数。

停电量可由停电时间、停电次数和负荷容量相乘得出，不再单独计算。

1.2.2 经济性指标

按照现阶段市场价格计算经济指标。为突出重点，只分析设备（MMC、DCCB、线路、换流站、变压器）成本、停电成本。

1.3 DG出力模型

在24 h内对光伏出力进行划分，典型出力时序如图2所示[11,12]。

图2 光伏出力时序Fig. 2 PV output sequence

1.4 负荷功率模型

典型负荷功率模型如图3所示[13]。

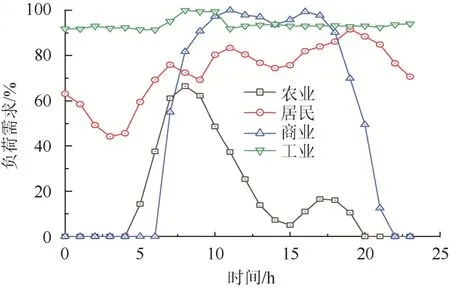
图3 负荷时序Fig. 3 Load sequence

2 目标函数

2.1 目标函数

在混合交直流配电网中，对直流线路始端需要额外加入MMC和DCCB。MMC和DCCB这2部分以及停电成本为可变成本；线路改造成本、换流站成本和变压器成本由负荷确定，可视为固定改造成本。因此，这里着重分析可变成本的经济性对总体成本影响。

总目标函数表达式为：

式中：CA为总体成本；CMMC为MMC配置成本；CDCCB为 DCCB配置成本；Closs为总停电成本；Cs为固定改造成本。

2.2 设备改造成本分析

2.2.1 MMC成本

总MMC成本为各个MMC成本之和。

单个MMC成本可以由半桥子模块（half-bridge sub module，HBSM）和全桥子模块（full-bridge sub module，FBSM）个数计算。总MMC成本表达式为：

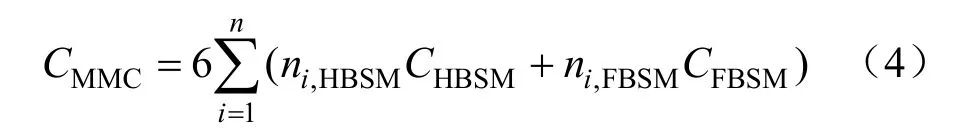
式中：n为需要直流改造区域的总数；ni,HBSM为第i个MMC单相半个桥臂所需HBSM模块数；ni,FBSM为第i个MMC单相半个桥臂所需FBSM模块数；CHBSM为HBSM单位成本，约3个绝缘栅双极型晶体管（IGBT）单位成本；CFBSM为FBSM单位成本，约5个IGBT单位成本[14]。

2.2.2 DCCB成本

DCCB负责隔离短路故障电流。在直流改造后，线路中的交流断路器将被DCCB取代。DCCB成本表达式为：

式中：ni,DC为第i个区域需配置的DCCB的个数；Ci,DCCB为第i区域所用DCCB单位成本；ni,AC为第i个区域原本的交流断路器个数；Ci,ACCB为第i区域所使用的交流断路器单位成本。

2.2.3 固定改造成本

固定改造成本表达式为：

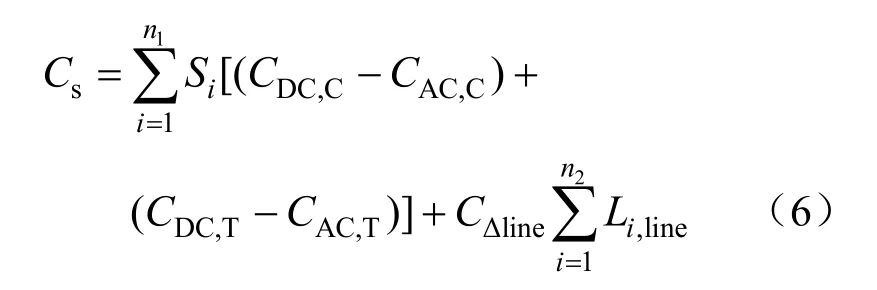
式中：n1为总共需改造区域的个数；Si为第i个区域的总负荷容量；CDC,C为单位容量直流换流站成本；CAC,C为单位容量交流变电站成本；CDC,T为单位容量直流变压器成本；CAC,T为单位容量交流变压器成本；n2为总共需改造线路的个数；Li,line为第i个区域线路的长度；CΔline为单位长度的交流线路和直流线路的差价。

2.3 停电成本分析

停电成本的表达式为：

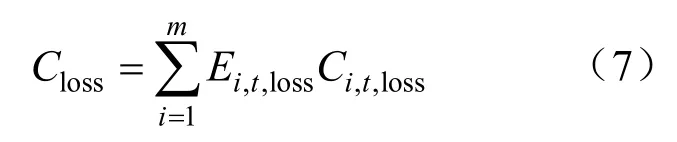
式中：Ei,t,loss为停电时间为t时第i个负荷的停电电量；Ci,t,loss为停电时间为t时第i个负荷的单位停电量成本；m为负荷区域总数。

各类型负荷的停电时长成本均根据表1拟合，拟合表达式为[15]：

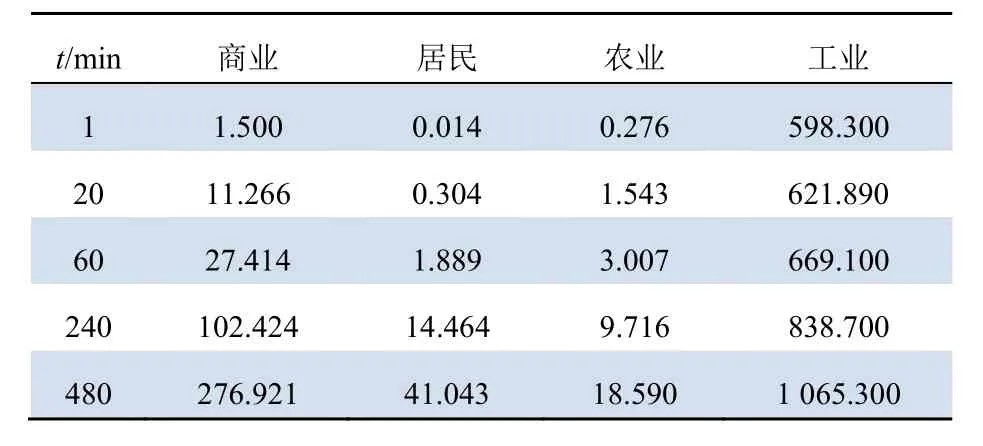
表1 负荷停电成本Tab. 1 Load outage cost元/(kW·h)

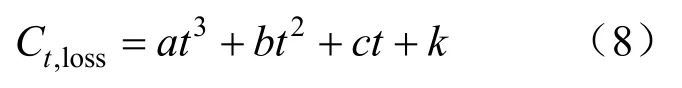
式中：Ct,loss为停电时间为t时的单位停电量成本；a、b、c、k为函数拟合系数，因不同负荷类型而不同。

各个类型负荷停电量与停电成本如表1所示[16,17]，拟合系数如表2所示。

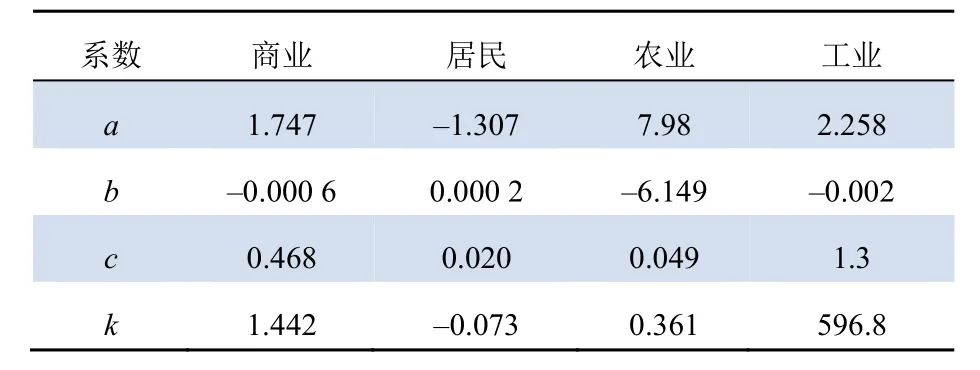
表2 拟合系数Tab. 2 Fitting coefficient

2.4 目标函数约束

以总经济性最优为原则时，改造方案的总成本应小于未改造方案的总成本。以可靠性最优为原则时，改造方案的停电成本应小于未改造方案停电成本，表达式为：

式中：CA,ref为改造后的方案总成本；CA,unref为未改造的方案总成本；Closs,ref为改造后方案停电成本；Closs,unref为未改造的方案停电成本。

3 MMC可靠性分析

在以往的包含MMC的配电网可靠性分析中，MMC可靠性模型采用的是子模块固定故障率模型。此时，子模块按照固定故障率分析，并认为各个子模块无相互影响；MMC可靠性由子模块的可靠性线性计算得到。在电压完全均衡分配的工况下，此可靠性模型能得到比较精确结果[18,19]。

在 MMC实际运行时，受切换、相间换流等多种因素影响，子模块电压并非完全均衡分配；所以，需分析子模块间的相关性，以得到MMC可靠性的准确数值[18-20]。以子模块可靠性为变量，不易求得其准确的概率分布，但可求得边缘分布。通过数学分析，其多维联合分布函数可由边缘分布函数和描述相关关系的copula函数来表示。实际应用中，考虑到不均衡电压较小，选用描述弱正相关的Gumbel函数，生成元为φ1/(1-θ)=(-lnu)1/(1-θ)，表达式为[20]：

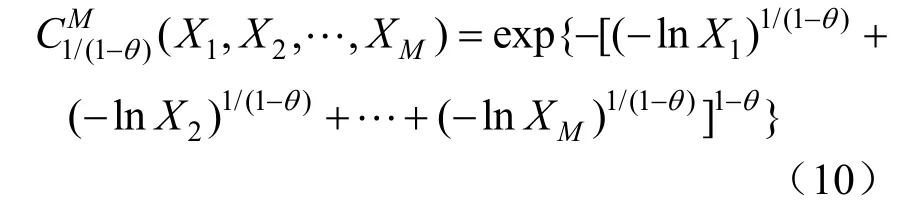
式中：θ取值（0,1），为相关程度参数，由极大似然估计求得；Xi为第i个子模块的寿命；M为变量维数。

以HBSM为结构的MMC子模块在相关性解耦后，桥臂可靠性表达式为[20]：

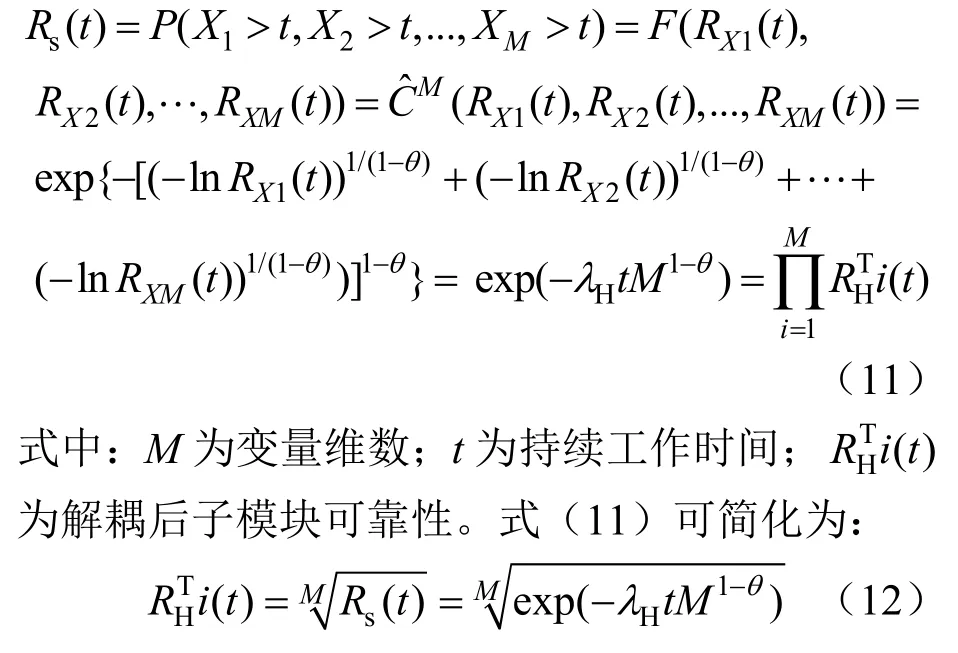
4 目标函数求解

狼群优化算法（gray wolf optimization，GWO）相较于粒子群等经典算法有更强的鲁棒性和更好的全局寻优能力；在处理多目标函数时，GWO相较经典算法收敛更快[21]。

GWO对初始值的要求较高。针对所研究问题，本文对GWO做如下改进：

（1）人工设定初始值。令全 HBSM 结构的MMC下的解为Xα，全FBSM结构的MMC下的解为Xβ，50%HBSM和50%FBSM结构的MMC下的解为Xδ，其对应适应度值分别为f(Xα)、f(Xβ)、f(Xδ) 。

（2）在迭代过程中，只有在更新当前最优解时，α、β、δ三者才进行移动。更新表达式为：

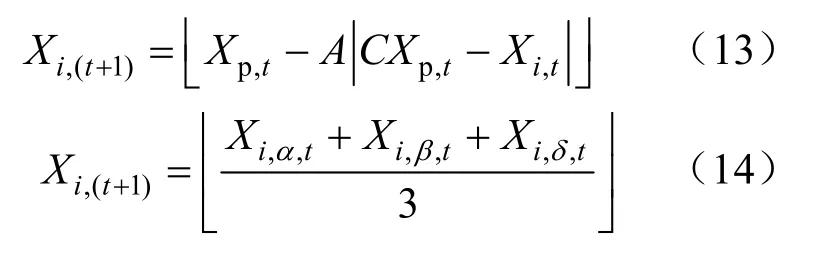
式中：Xi,(t+1)为下一时刻i的位置；Xi,t为此时刻i位置；Xp,t为此时刻目标位置（Xi,α,tXi,β,tXi,δ,t）；A、C为系数；“”为向下取整函数。

考虑到所研究的设备均以整数进行变化，所以设定每个个体移动步长均为“去 1法”整数步长，防止出现小数计算影响与实际问题的贴切度。

具体评估流程如图4所示。

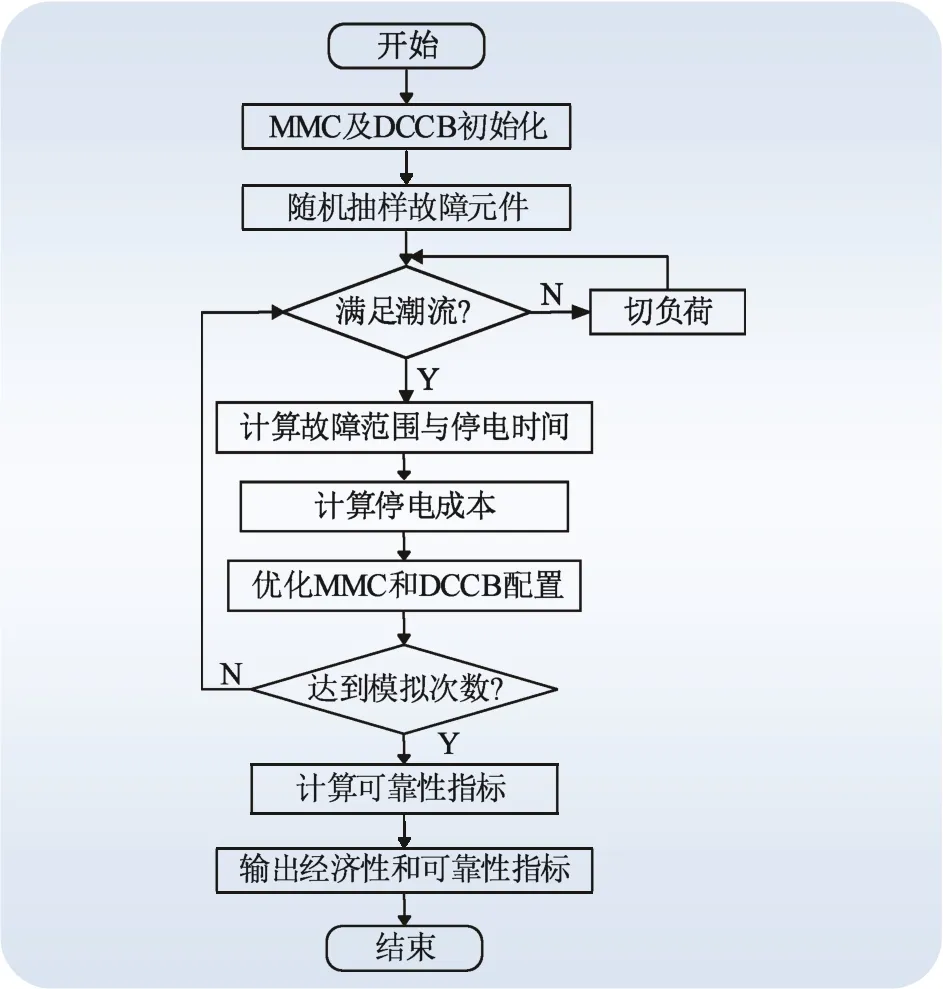
图4 评估流程Fig. 4 Evaluation process

5 算例分析

5.1 算例介绍

算例：IEEE RBTS-BUS6直流改造。

将3个直流区域编号为 1，2，3；各直流区域均可连接其他直流网络或DG。直流区域1中，主干线路电压等级为10 kV，交流变压器变比为10 kV/380 V。直流变压器变比为DC 10 kV/DC 400 V，直流负荷电压等级为400 V。MMC整流电压为AC 10 kV/DC 10 kV。MMC单相半桥臂总模块数为6。在3部分直流区域的首端MMC中，HBSM和FBSM比例以及DCCB数量均为待配置状态；在MMC中，FBSM比例超过43%，且在MMC具有切断直流短路电流能力时，相应区域不再配置DCCB[10]。设定HBSM和FBSM所用IGBT的额定电压为1 kV、额定电流为1 kA，单价为400元。

各方案具体如下：

方案1：为对照方案。不进行直流改造，只添加AC/DC设备为直流负荷供电。

方案2：3处MMC配置均采用全HBSM结构；为保证切断短路电流能力，各直流区域均配置DCCB。

方案3：为根据本文方法配置的混合结构MMC。

方案4：3处MMC均采用FBSM结构，各直流区域不再配置DCCB。

按照以上方案分别对各方案的MMC进行子模块解耦计算。子模块内部元件故障率如表3所示[22]。根据所生成的子模块元件指数寿命分布规律数据，求得θ=0.05；解耦后的可靠性如图5所示。

表3 子模块元件故障率Tab. 3 Sub-module component failure rate

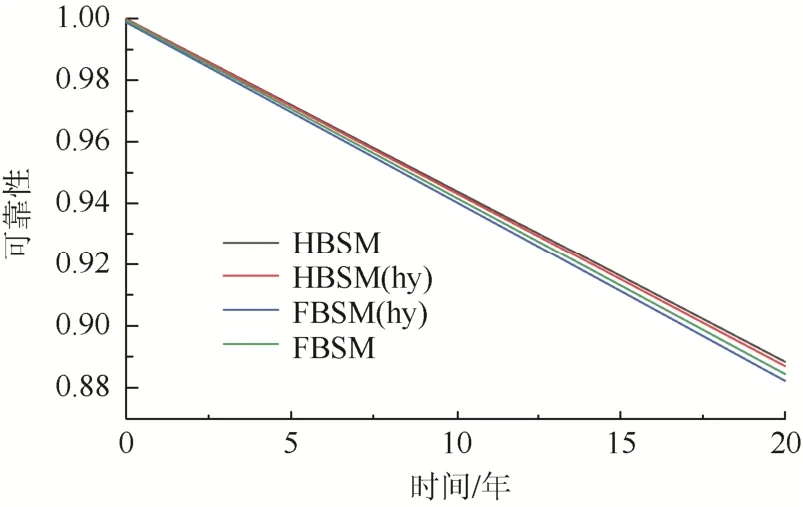
图5 子模块解耦后可靠性Fig. 5 Reliability after sub-module decoupling

图5中，HBSM为方案2中MMC解耦后可靠性曲线，HBSM（hy）和FBSM（hy）为方案3解耦后可靠性曲线，FBSM为方案4 解耦后可靠性曲线。

以24 h制对负荷和DG进行时序蒙特卡洛抽样。模拟 10次取平均值，单次模拟计算周期为100。

负荷数据参见文献[22]。配电网网架结构如图 6所示。各方案初始配置如表4，元件相关参数如表5所示[8,22-25]，其中T1、T2、T3为修复、替换和倒闸操作时间。

图6 网架拓扑Fig. 6 Grid topology

表4 方案初始配置Tab. 4 Scheme initial configuration

表5 设备及其所需参数Tab. 5 Equipment and its required parameters

考虑直流电能传输的优势，直流线路具有相对于交流线路更低的成本，故取直流线路成本约为交流线路的一半，改造线路共计长29.05 km。因为方案1中AC/DC只面向低压小容量负荷，所以在计算方案成本时忽略[25]。

做如下限定：

（1）鉴于多重故障的概率很低，本文只考虑N–1情况。

（2）直流线路换流器采用双极接线结构。

（3）直流改造线路中，不对负荷容量大小进行更改，只更改负荷为直流性质。

（4）直流设备修复、切换时间见文献[6]。

5.2 计算结果及分析

5.2.1 备用支路接入其他直流网络

首先，不考虑DG，按照备用支路接入其他直流网络的情况，根据本文模型及算法对算例拓扑进行MMC配置。各直流区域首端MMC结构配置如表6。分别以蚁群、粒子群、狼群算法计算可靠性并对计算时长进行对比，结果如表7所示。表7中，ASAF为SAIFI，ASAD为SAIDI。

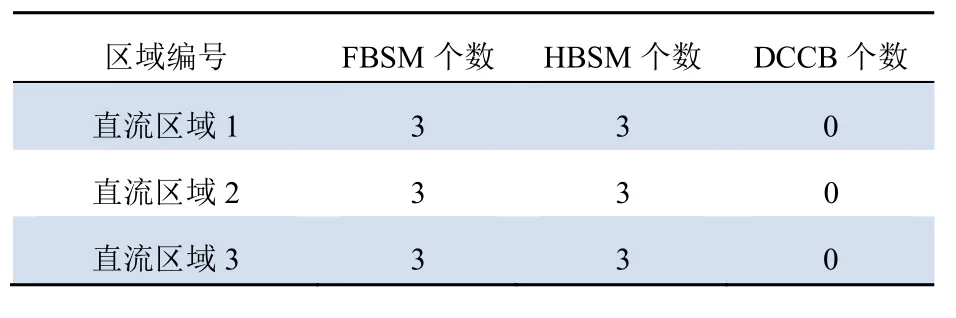
表6 本文方案MMC配置Tab. 6 MMC configuration of scheme of this paper

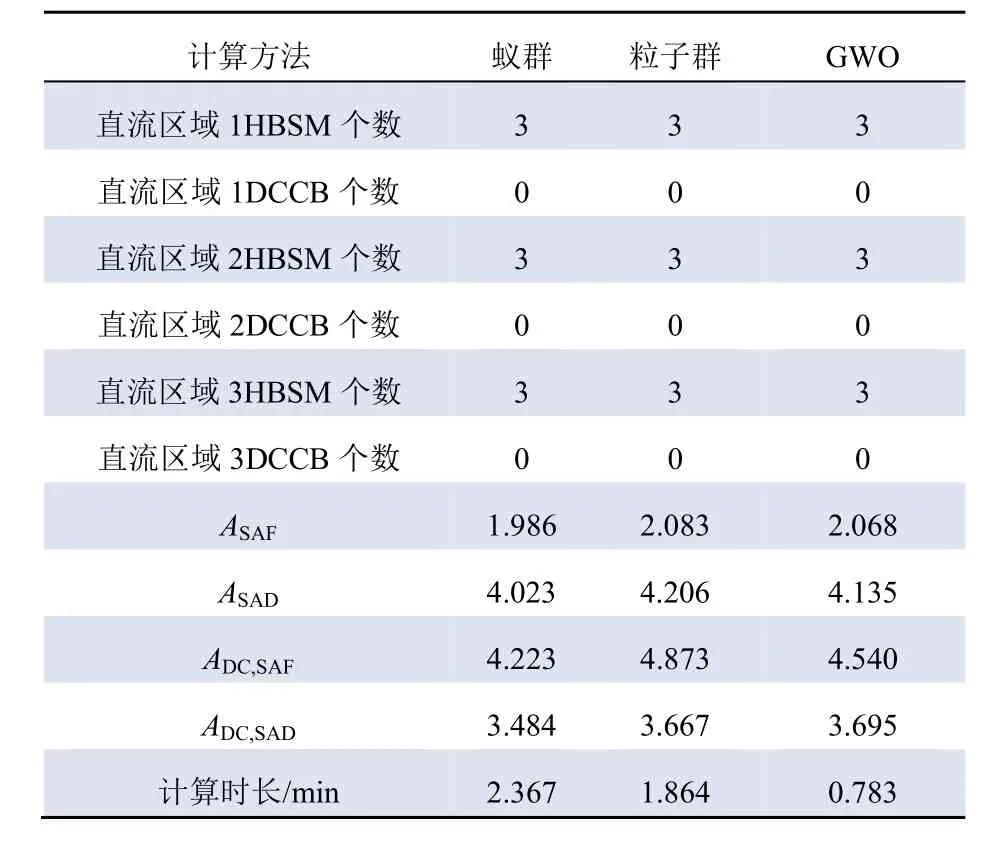
表7 不同算法计算情况Tab. 7 Calculation by different methods

由表6可以看出，狼群算法、粒子群算法和蚁群算法的各项可靠性指标计算精度误差均在10%以内，狼群算法的计算速度相对于粒子群算法和蚁群算法有明显优势。

（1）各方案停电成本分析。

按照本文方法，各方案的成本计算结果如表8所示。表8中，方案2、方案3、方案4除停电成本外，其他各项成本都相对于方案1做了归算。

表8 各方案成本分析Tab. 8 Cost analysis of each scheme万元

从表 8可以看出，在停电成本方面，方案 1的停电成本最大。这是因为方案1使用了较多的AC/DC代替交流变压器，而现阶段AC/DC的故障率还比较高，容易导致负荷停电。其他方案成本均小于方案1，这说明在高比例低压直流负荷情况下，建设 MMC换流站能在较大程度上提升供电可靠性。

方案2停电成本最小。这是因为HBSM的故障率低于FBSM，且DCCB可以作为切断直流短路电流的后备，限制了停电影响范围。

方案3停电成本接近于方案2而小于方案4。这是因为混合结构的MMC故障率小于全FBSM结构的MMC，所以方案3停电的可能性小于方案4；但因为没有DCCB限制故障范围，所以停电成本要略高于方案2。

（2）各方案总成本分析。

对比各方案总成本可以发现，即使在不计AC/DC成本的情况下，相对于方案1，其他3种方案也均在总成本上具有优势。这说明，在高比例低压直流负荷情况下，进行 MMC换流站改造不仅能提升电网可靠性，而且电网经济性也要优于使用AC/DC代替交流变压器的方案。

方案2的总成本经济性优势最小。这是因为电网需要配备额外的DCCB用于切断短路电流；这增加了一大部分经济成本，而因此减小的停电成本不足以对其进行抵消。

方案4总成本高于方案3。这是因为全FBSM结构MMC的成本和故障率都比混合结构的MMC高。

方案3使用混合结构MMC，在提高可靠性的同时降低了成本。方案 3的经济性相对于方案 2和方案4分别提升了约48.751%和11.249%，这充分表明了本文方法的正确性。

（3）各方案可靠性指标分析。

各方案的可靠性评估结果如表9所示。

表9 各方案可靠性评估结果Tab. 9 Reliability evaluation results of each scheme

在SAIFI方面：方案1使用了较多的AC/DC设备，导致了系统故障率增加；方案3指标较高，是因为现阶段FBSM和HBSM的故障率较高。方案3使用了一定比例的FBSM且不使用DCCB，导致了方案3的故障范围限制能力稍弱。全FBSM结构的MMC可以进行反极性电压输出，这在一定程度上保证了供电的可靠性，减小了停电可能性。

在SAIDI方面：方案1使用较多AC/DC设备导致其停电可能性最大，停电范围也最大。在全FBSM结构的MMC配置中，没有DCCB作为后备，交直流区域受彼此影响较大，不能隔离故障，将导致更大范围停电，所以方案4发生大范围停电的可靠性最大。因此，方案4的单次停电时间要长于方案2和方案3。方案3的停电时间长于方案2也是因为没有DCCB作为后备。

在DCSAIFI方面：全FBSM结构的MMC发生故障导致直流区域停电的概率，要小于因为全HBSM结构MMC和DCCB发生故障导致直流区域停电的概率，从而减少了直流区域的停电次数：所以对于直流区域可靠性，MMC所产生的影响要显著于DCCB。

在DCSAIDI方面：因为方案4采用全FBSM结构MMC，没有DCCB作为后备，不能隔离故障，易导致大范围停电；所以，方案4的单次停电时长更长。方案2配置了更多的DCCB，而现阶段DCCB故障率还比较高；若DCCB发生故障，需由上一级的断路器切除故障，所以扩大了停电范围。方案3最优，这是因为混合MMC因FBSM故障而扩大故障范围的概率小于方案 2中因DCCB故障而扩大故障范围的概率。

综合表8和表9：相对于方案2，方案3停电成本仅增加了1.240%；相对于方案4，方案3停电成本节省了8.189%。所以，方案3的可靠性与经济性综合提升效果最好。

（4）DCCB成本变化影响分析。

当DCCB价格变化时，各方案的经济指标如表10所示。因为方案1、方案4和方案3中没有使用DCCB，所以其经济指标不变。方案2的经济指标在DCCB价格低于每组0.997万元时，才会优于方案4；在DCCB价格低于每组0.549万元时，才会优于方案3。可见，DCCB价格变化对方案之间相对经济性优劣影响很小。

表10 不同DCCB价格下各方案CATab.10 CA of each scheme under different DCCB prices

5.2.2 接入DG后总成本分析

将备用支路改换为 DG。用蒙特卡洛法根据DG的时序曲线进行抽样，模拟DG出力。将以上各方案接入DG。当各直流区域按统一渗透率（DG容量与总负荷容量的比）变化时，各方案成本变化如图7所示。

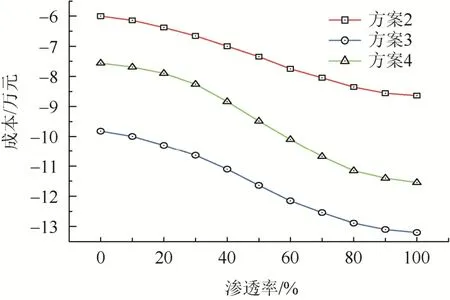
图7 不同渗透率下各方案成本Fig. 7 Scheme cost under different permeability

在不同渗透率下，方案3的成本仍然要少于方案2和方案4。即使在考虑DG出力随机性的情况下，方案3通过减少高故障率设备的使用，仍能在一定程度上减少设备成本和停电成本。

在 DG渗透率逐渐增加过程中，各方案成本的总体变化趋势相同。在渗透率为 80%～100%阶段，各方案成本下降逐渐减缓；而在40%～75%阶段，3个方案成本下降最快。

各方案的成本变化趋势差别：方案2的变化趋势最小，在渗透率为40%～60%阶段达到最快下降速度；方案3的变化趋势稍快于方案2，并在渗透率为50%～70%时达到最快下降速度；方案4的变化速度最高，在渗透率为60%～75%时达到最快下降速度。

在低渗透率时，DG出力很小，其作为停电后备效果较弱。方案2因为全HBSM结构的MMC故障率低且使用了DCCB可以很好地隔离故障，所以其受DG的随机性影响较小。而方案4的情况与之相反，且在渗透率为60%～75%时，DG的容量刚好满足至少一半负荷；因为大范围停电的概率很小，所以此时刚好能解决小范围停电问题。方案3虽然隔离故障能力弱于方案2，但是发生故障的可能性较小，所以受 DG影响较为折中；同样，方案3对于小范围停电解决效果较好。

通过以上分析，可以得出结论：在使用不同配置方案时，设定不同DG渗透率范围，可以使成本下降趋势达到更高；但是，对于较高比例的低压直流负载，应尽量设置DG的渗透率范围在50%～75%。