基于最小二乘支持向量机的组合模型在区域似大地水准面拟合中的应用

李明飞 吴军超 张一驰

1 陕西省土地工程建设集团有限责任公司，西安市光泰路7号，710075 2 华南师范大学地理科学学院，广州市中山大道西55号，510631 3 广东省智慧国土工程技术研究中心，广州市中山大道西55号，510631

在高程测量中，GPS 获取的高程数据为大地高，而我国所采用的高程系统为正常高[1]，两者存在差值，即高程异常。因此，如何获取高精度的高程异常是区域似大地水准面拟合的关键。

LSSVM是一种常用的区域似大地水准面拟合方法，其以支持向量机为基础改进而来，在高程转换过程中能够取得较好的效果[2]。但单一的LSSVM会存在模型误差，精度有限，且会造成拟合残差序列信息浪费。基于此，本文以LSSVM为基础，提出LSSVM-Shepard组合区域似大地水准面拟合方法，充分利用拟合的残差序列信息，减少模型误差影响，提高高程转换精度。

1 原理与方法

1.1 LSSVM原理

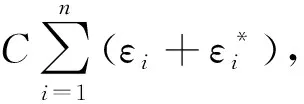
假设(xi,yi)为一组高程异常数据集，其中，i=1,2，…，n，xi∈Rl，yi∈R。xi为数据集的平面坐标，yi为数据集的高程异常。则LSSVM优化问题为：

(1)

式中，ω为系数序列，e为误差项，γ为正则化参数，φ(·)为映射函数，b为偏差量。根据拉格朗日定理可得：

L(ω,b,e,α)=J(ω,e)-

(2)

分别对ω、b、ei、αi求偏导数，并使偏导数等于0。整理得：

(3)

根据Mercer条件可知[6-7]，存在映射函数φ和核函数K，使得K(xk,xl)=φ(xk)Tφ(xl)。线性方程组(3)整理可得：

(4)

通过解方程(4)可得αi和b，则LSSVM模型函数可表示为：

(5)

1.2 Shepard插值模型

Shepard插值模型是针对大量离散点提出的局部逼近模型，是一种改进的加权平均法[8]。该模型应用于高程转换的主要原理为：对于给定的数据集(xi,yi,ξi)，i=1,2，…，n，(xi,yi)为平面位置坐标，ξi为对应的高程异常，则未知点高程异常可通过下式进行求解：

(6)

式中，u为拟合度，u>1；ri为未知点到各已知点的距离；ρ(ri)为已知点关于未知点的距离权函数：

(7)

从式(7)可以看出，影响范围内会形成两个环带。

1.3 LSSVM-Shepard组合模型

根据物理大地测量学理论，高程异常可分为3个分量[9]，其公式为：

ξ=ξ长+ξ中+ξ短

(8)

式中，ξ长、ξ中、ξ短分别为长波、中波、短波分量。高程异常在中长波项部分趋势变化平缓，而在短波项部分变化较大，容易受到地形等因素影响。

LSSVM将最小二乘思想引入到支持向量机，趋势面变化相对平缓，同时保持支持向量机良好的非线性问题处理能力，可提高计算效率。与二次曲面拟合“移去-恢复”模型的中长波项相比，LSSVM能够更好地处理中长波项中存在的非线性问题。Shepard插值模型可以充分利用周围已知点信息，能够有效处理局部变化信息。本文将两个单一模型进行结合，采用LSSVM拟合高程异常的中长波项，利用Shepard插值模型拟合包含模型误差的短波项，综合两个单一模型的优点，同时充分利用单一模型的拟合残差信息。其主要步骤如下：

1)利用LSSVM对高程异常的中长波项进行拟合，确定模型系数，并计算包含LSSVM模型误差和短波项的残差序列。

2)利用Shepard插值模型对残差序列进行训练，使用交叉验证方法确定模型系数。

3)利用组合模型计算区域内任意一点的高程异常值。

2 算例分析

2.1 项目概况

实例1 项目区位于黑龙江省某市，地势较为平坦，属于平原地区。项目区共有74个GPS C级网点，且均已进行二等水准联测[ 10]，测区面积为1 100 km2。点位分布见图1。

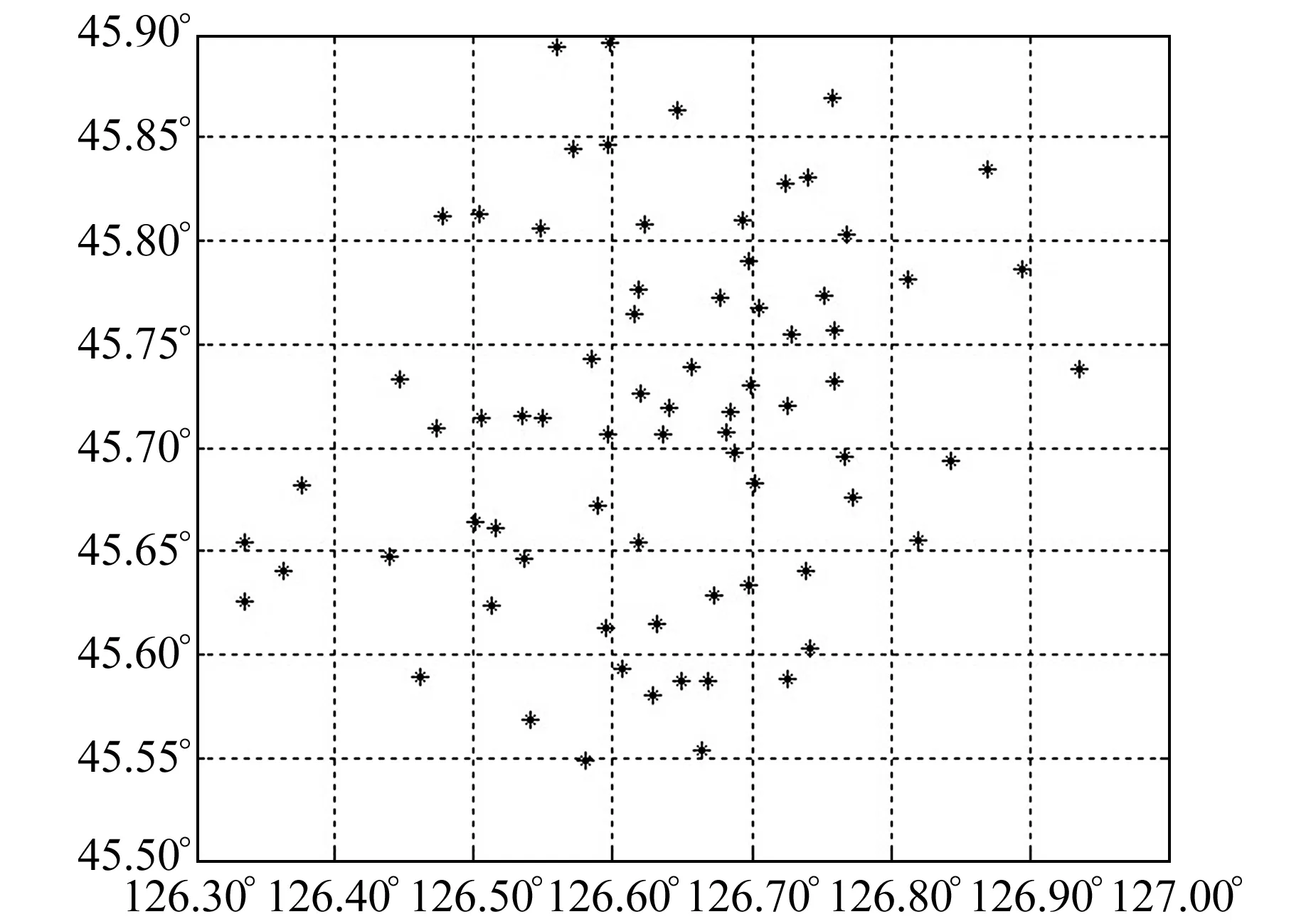
图1 平原地区GPS点位分布Fig.1 Distribution of GPS points in plain area

实例2 似大地水准面拟合项目区位于云南某地区，区域内地形起伏大，属于高原山区地形。区域内共布设24个C级GPS 控制点，并已进行三等水准联测[11]，测区面积约为2 159 km2。点位分布见图2。

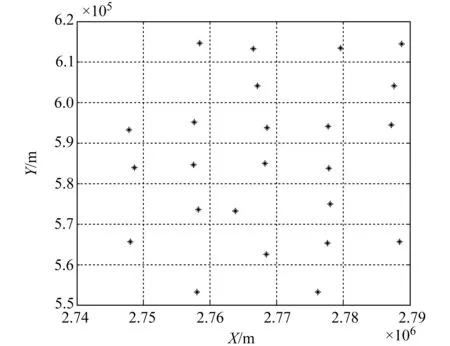
图2 高原山区GPS点位分布Fig.2 Distribution of GPS points in plateau mountainous area

2.2 参数选取

LSSVM模型采用径向基函数作为核函数，其公式为：K(x,xi)=exp(-‖x-xi‖2/2σ2)。该模型含有2个参数，分别为惩罚系数γ和核函数参数σ，模型参数以双层方格网法进行寻优。同时为减少取样随机性所产生的训练偏差，采用交叉验证法进行参数精度评定，将原始数据分为n等份，通过n次循环，每次以其中一份作为测试数据，其余n-1份作为训练数据，得到模型并对测试数据进行预测。统计测试结果，最终获得n次统计结果的平均值，并以此作为参数的评价因子。Shepard插值模型参数为拟合度u和影响半径R，为防止模型陷入局部最优，文中将u和R范围分别设置为[1,50]和[0.1,20]，搜索步长分别设置为1和0.02，同时通过循环操作使寻优过程遍历每一个节点。

2.3 实验对比分析

为增加实验的可靠性，选取10、20、30、40、50个均匀分布的联测点分别作为平原地区实验拟合点，选取7、9、11、13、15个均匀分布的联测点分别作为高原山区实验拟合点，剩余点作为检测点进行计算。为使高程异常数据集处于同一量级，在实验前对两组数据分别进行标准化处理。

实验分别采用二次曲面法、LSSVM、Shepard插值模型、二次曲面-Shepard、LSSVM-Shepard模型等5种方法进行似大地水准面拟合，采用检测点的外符合精度作为评定指标。实验计算结果如表1(单位m)和表2(单位m)所示。

表1为平原地区各模型计算结果对比。当拟合点个数从10增加至50时，LSSVM-Shepard模型的外符合精度从0.035 m降至0.015 m，且数值均小于二次曲面、LSSVM、Shepard插值等3种单一模型，说明该组合模型的拟合效果优于这3种单一模型。二次曲面-Shepard模型随着拟合点数增加，外符合精度从0.034 m降为0.013 m，且数值均小于二次曲面和Shepard插值模型，说明拟合效果优于这两种单一模型。当拟合点个数一定时，二次曲面-Shepard和LSSVM-Shepard模型的外符合精度最大差值的绝对值为0.002 m，表明两个组合模型的拟合效果基本一致。

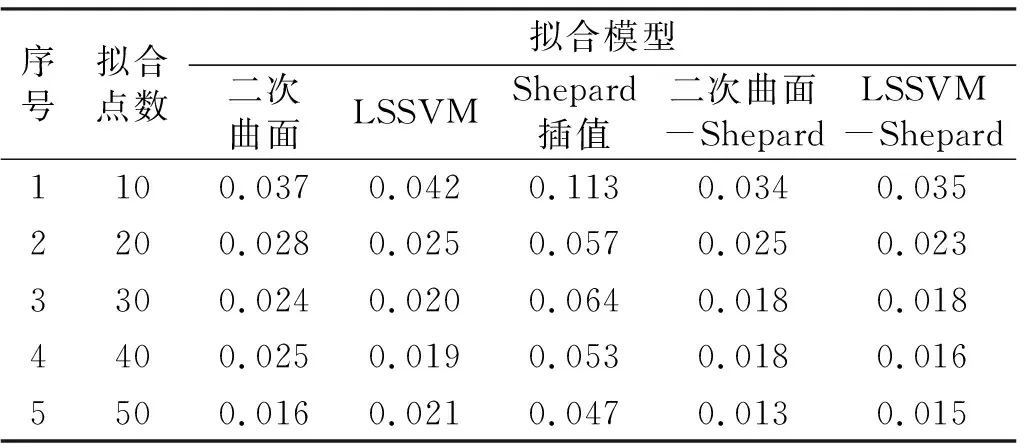
表1 平原地区似大地水准面拟合结果统计

表2为高原山区各模型计算结果对比。当拟合点个数一定时，LSSVM-Shepard模型的外符合精度小于其他4种模型，说明该组合模型高程转换效果最优。当拟合点个数由7增加至11时，二次曲面-Shepard模型的外符合精度分别为0.097 m、0.103 m、0.110 m，而Shepard插值模型的外符合精度分别为0.095 m、0.094 m、0.089 m，Shepard插值模型的拟合效果略优，说明二次曲面-Shepard模型在复杂的高原山区进行高程转换时适用性受限。

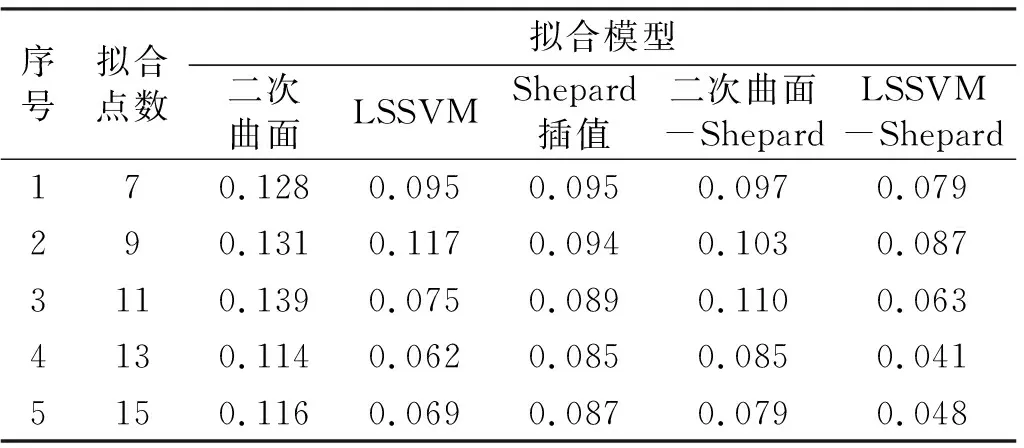
表2 高原山区似大地水准面拟合结果统计

综上所述，无论是在平原还是高原山区实验区，LSSVM-Shepard模型的拟合效果均优于二次曲面、LSSVM、Shepard插值等3种单一模型。在平原实验区，LSSVM-Shepard模型和二次曲面-Shepard模型均能取得较好的拟合效果，但在高原山区实验区，二次曲面-Shepard模型适用性受限，而LSSVM-Shepard模型仍能取得较好的拟合效果。

3 结 语

本文提出LSSVM-Shepard组合区域似大地水准面拟合方法，并结合平原地区和高原山区两个工程实例进行实验，得到以下结论：

1)无论是在平原地区还是高原山区，LSSVM-Shepard模型的拟合效果均优于二次曲面法、LSSVM、Shepard插值等3种单一模型，是一种可行的似大地水准面拟合方法。

2)二次曲面-Shepard模型在平原实验区进行高程转换时，能够取得较好的拟合效果，但在高原山区实验中，转换度低于Shepard插值模型，适用性受限。LSSVM-Shepard模型以LSSVM代替二次曲面模型，能够有效处理转换过程中的非线性问题，在两个实验中均能取得较好的高程转换效果，具有较强的适用性。