基于PD反馈控制的音圈电机直驱式微动台直线度补偿技术

李 奇

(季华实验室，广东 佛山 528200)

0 引 言

在平板曝光、晶圆光刻、显示面板检测与修复[1-4]等高精度装备中，为了保证工件与加工工具之间精确的相对位置关系，一般采用宏动-微动台技术。音圈电机直接驱动的微动台结构，具有精度高、响应快、推力大等优点，广泛应用于半导体精密加工等领域[5-7]。

关于音圈电机直驱微动伺服系统设计与控制方法，很多学者做了大量的研究探索。KIM等[8]提出一种包含柔性铰链与电涡流阻尼器的纳米定位台。柔性铰链和电涡流阻尼器分别为定位台提供刚度和阻尼，定位台具有合适的阻尼比，缩短了调节时间。定位台获得较好的数值和试验结果。KIM等[9]介绍了一种用于半导体微纳加工、显示面板检测的精密伺服定位台。该定位台的微动台采用多个音圈电机驱动，与宏动台之间无机械耦合，定位精度达数十纳米。TSUMURA等[10]研究了一种气体静压式轴承-导轨高速定位台，定位台带磁力预加载，具有纳米级定位精度。仇礼钦[11]介绍了一种由音圈电机和磁悬浮补偿器搭建的z-Rx-Ry三自由度定位台，基于音圈电机良好的动态特性，取得了较好的试验结果。王福超等[12]采用完全控制跟踪方法(PTC)对音圈电机驱动快速反射镜进行控制，有效改善系统的动态性能，拓展控制带宽。邢向[13]研究了一种基于音圈电机的大行程双自由度快速刀具伺服装置(FTS),建立了整体闭环控制函数，对装置的刚度、阶跃响应等方面进行了分析与测试。

本文采用音圈电机直驱式微动台机构，建立了喷墨打印扫描轴直线度误差补偿系统。设计了结构紧凑的挠性弹簧，为微动台提供足够的刚度。分析了基于音圈电机的直线度误差补偿系统的数学模型，并根据该系统的机械结构及其控制要求，设计了位置反馈控制器。为满足系统的响应时间和超调量要求，提出基于PD控制的位置闭环控制器，引入虚拟刚度和虚拟阻尼，大幅缩短了响应时间和超调量。本文提出的直线度补偿方法，有效地提高了系统的打印精度。

1 喷墨打印宏动-微动台系统构成

本文以精密运动控制为核心，建立了基于喷墨打印的宏动-微动台系统，如图1所示，该系统可对扫描主轴进行直线度误差补偿。具体工作原理：在喷印运动平台上，宏动台沿扫描主轴做往复直线运动，微动台安装在宏动台上，微动台上的吸盘能够稳定地保持住工件(玻璃基板)。喷头固定在喷头模组上，喷头模组沿步进主轴做点到点直线运动。扫描主轴和步进主轴都由直线电机驱动。受限于导轨加工精度，扫描主轴存在几何误差，其中水平直线度误差是影响打印精度的主要因素，扫描主轴长度超过3米，水平直线度误差达数十微米。要完成高精度喷墨打印，必须通过微动台进行误差补偿。

图1 喷墨打印宏动-微动台系统

喷墨打印过程如图2所示，喷头模组沿步进主轴移动到指定位置，宏动-微动台在扫描主轴上往复运动，在此过程中，喷头模组中的喷嘴将墨滴准确地喷射到相应的子像素槽中。

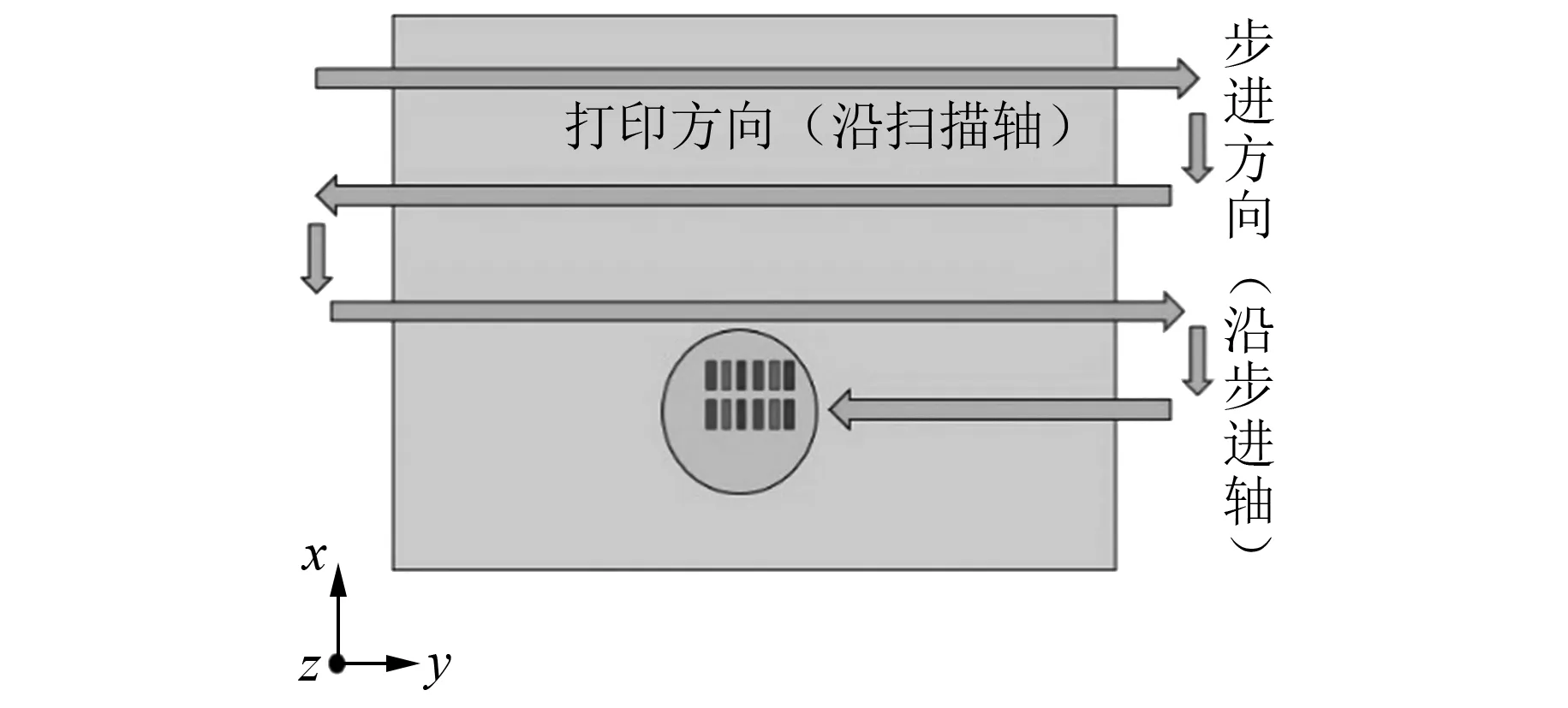
图2 步进-扫描喷墨打印过程示意图

宏动-微动台音圈电机布局如图3所示，音圈电机定子安装在宏动台底板上，音圈电机动子连接传动机构，传动机构完成多自由度解耦。通过对应的正逆运动学公式，4个音圈电机可实现微动台x-y-z3个自由度微小运动。具体方法：y轴音圈电机同向平移，控制微动台沿y轴方向运动；x轴音圈电机同向平移，控制微动台沿x轴方向运动；x轴或y轴音圈电机异向平移，控制微动台绕z轴旋转运动。

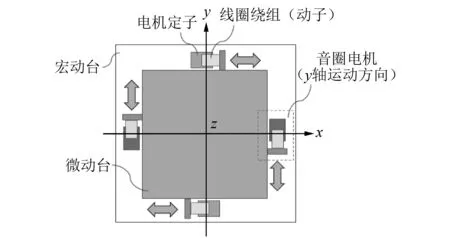
图3 宏动-微动台音圈电机布局图

2 音圈电机直驱式微动台及数学模型

2.1 音圈电机基本原理及结构

音圈电机是一种特殊形式的直接驱动电机，如图4所示，结构与扬声器类似[14]。其工作原理为：通电线圈(导体)在磁场中会产生力，力的大小与施加在线圈上的电流成比例。基于此原理制造的音圈电机运动形式可以为直线或者圆弧。

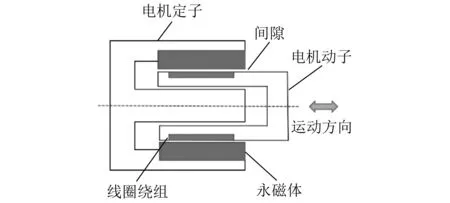
图4 音圈电机结构

电磁力方程：

Fe=BlNi=kei

(1)

电机力常数：

ke=BlN

(2)

音圈电机线圈绕组存在反电动势，大小为

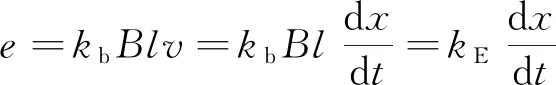
(3)

式中：N为线圈匝数；l为每匝线圈导体处在磁场中的平均有效长度；B为线圈所在空间的磁感应强度；i为线圈导体中的电流；kb为反电动势系数；kE为反电动势常数。

如图5所示，设音圈电机线圈绕组端施加电压为u，线圈电阻为R，电感为L，线圈回路的动态电压平衡方程为

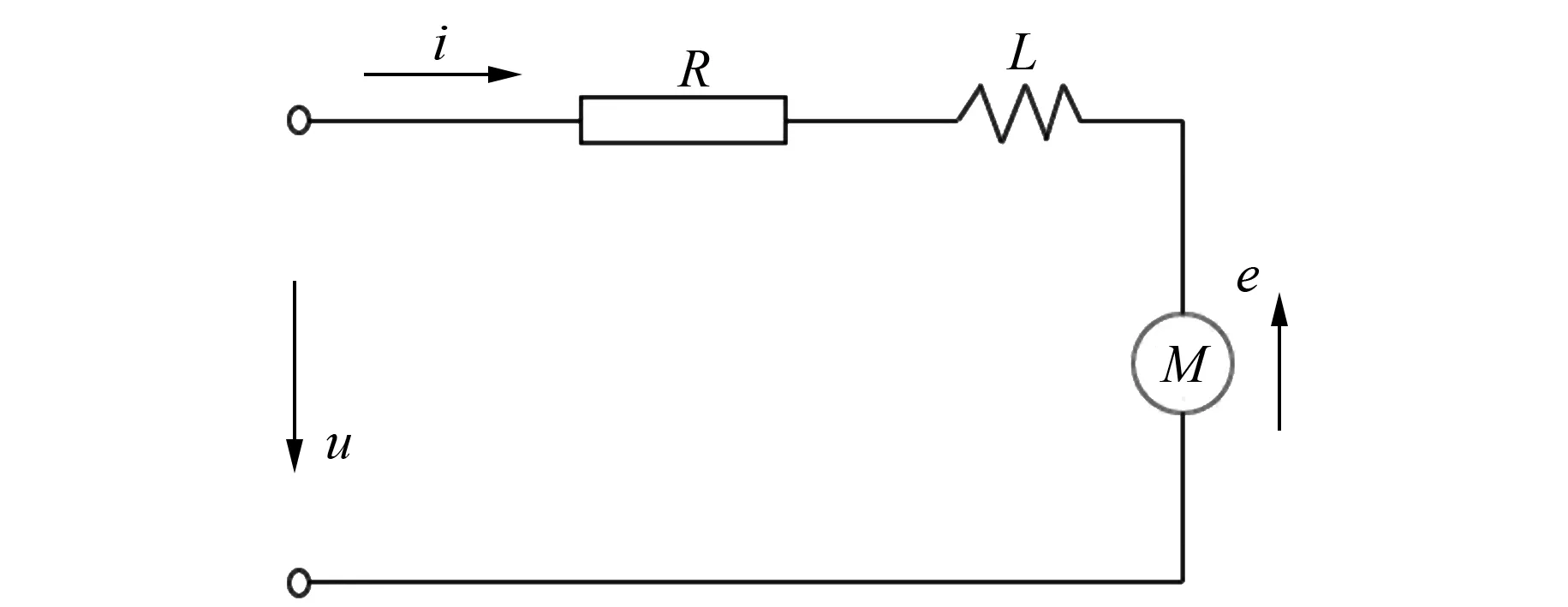
图5 音圈电机等效电图图

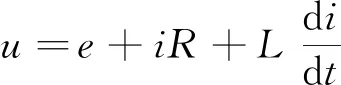
(4)

2.2 直驱式微动台受力分析

直驱式微动台结构如图6所示，音圈电机定子固定在宏动台，动子与微动台固连，微动台和宏动台之间装有精密直线导轨。为简化模型，只对一个音圈电机及相应负载进行受力分析，如图7所示。音圈电机为微动台提供电磁推力Fe，微动台与宏动台做相对直线运动。运动过程中，微动台受到摩擦力f、速度阻尼力Fd、弹簧弹力Fk、外部扰动力fd。

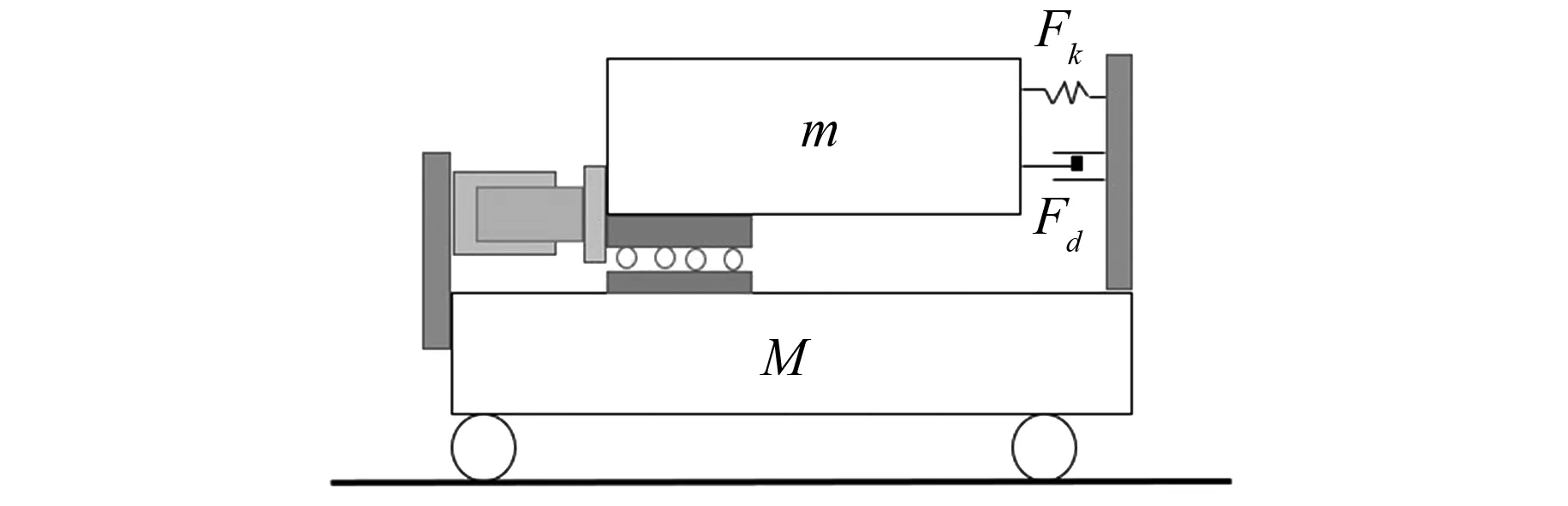
图6 微动台结构简图

图7 质量-阻尼-弹簧微动台系统

微动台力平衡方程：

F=Fe+fd-f-Fd-Fk

(5)

根据牛顿第二定律：

F=ma

(6)

微动台加速度：

(7)

式(5)中摩擦力f为干摩擦力，可认为是一个恒定值。Fd为黏性摩擦力，与微动台速度成正比：

(8)

式中：d为速度阻尼系数。

精密直线导轨的干摩擦力与黏性摩擦力相比非常小，可忽略不计，外扰力暂不考虑。弹簧弹力也是微动台运动的阻力，表达式为

Fk=kx

(9)

式中：k为挠性弹簧弹力系数。

将式(6)～式(9)代入式(5)，得到：

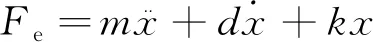
(10)

2.3 微动台数学模型

根据微动台的受力分析，联立式(1)、式(4)、式(10)，构成微动台运动方程组：

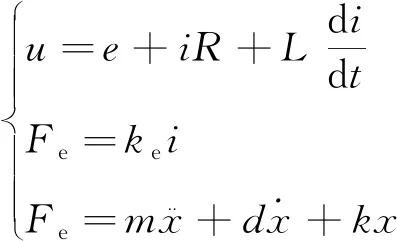
(11)

从式(11)可得到微动台位移输出x与音圈电机电压输入的微分方程：

(12)

由式(12)可得微动台位移输出x与音圈电机电压输入u之间的传递函数：

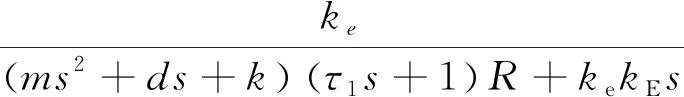
(13)

可得到微动台位移x与音圈电机推力Fe之间的传递函数：

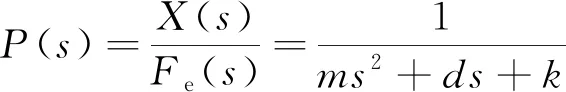
(14)

3 微动台系统设计

3.1 音圈电机与精密直线导轨选型

微动台系统音圈电机采用雅科贝思AVM100-HF-10，具体参数如表1所示。精密直线导轨选择THK VR1-20Px5Z交叉滚柱导轨，P级精度，最大行程12 mm。精度曲线如图8所示,可见100 mm行程内，导轨平行度在2 μm以内。

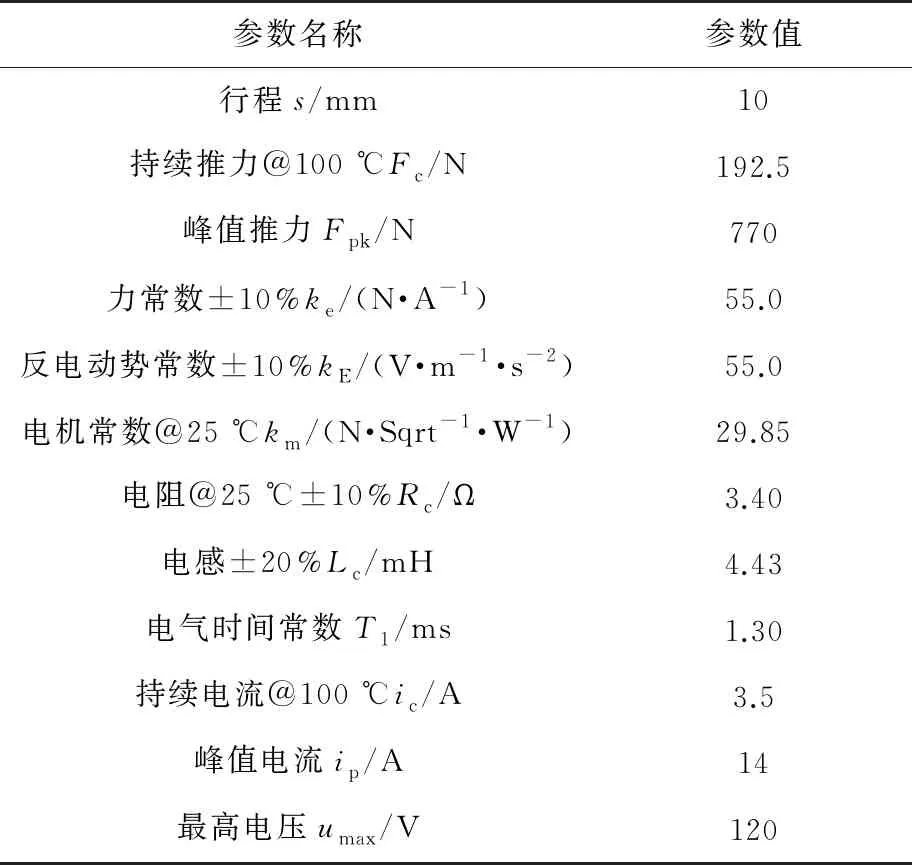
表1 音圈电机主要参数

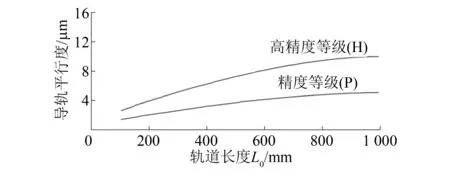
图8 THK VR系统导轨精度曲线

3.2 挠性弹簧的设计

为了让微动台具有较好的动态特性，需要引入一个弹簧来增加系统刚度。由式(15)可知，直驱式微动台为典型的二阶质量-阻尼-弹簧系统。系统固有频率为

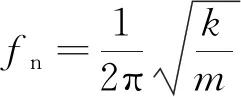
(15)

根据胡克定律，弹簧最大变形力：

Fk_max=kΔx

(16)

微动台质量m=100 kg，设定微动台响应频率fn≥5 Hz，代入式(11)得到弹簧刚度k≥9.86×104N/m，弹簧刚度k取105N/m。微动台沿xy方向行程为±1 mm，因此弹簧最大变形力为±100 N。微动台的速度阻尼力和摩擦力可忽略不计。由表1可知，音圈电机持续推力大于弹簧最大变形力，微动台能够运动。

考虑到微动台空间比较紧凑，设计一种与宏动台-微动台相适应的挠性弹簧。挠性弹簧的安装位置如图9所示，挠性弹簧的两端分别固定在宏动台和微动台上，需提供x和z两个刚度相等的自由度。为便于设计与分析，采用板簧来设计挠性弹簧。具体结构如图10所示。板簧材料为弹簧钢60Si2Mn，弹性模量E=206 GPa。

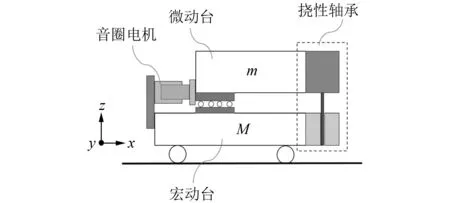
图9 挠性弹簧的安装位置

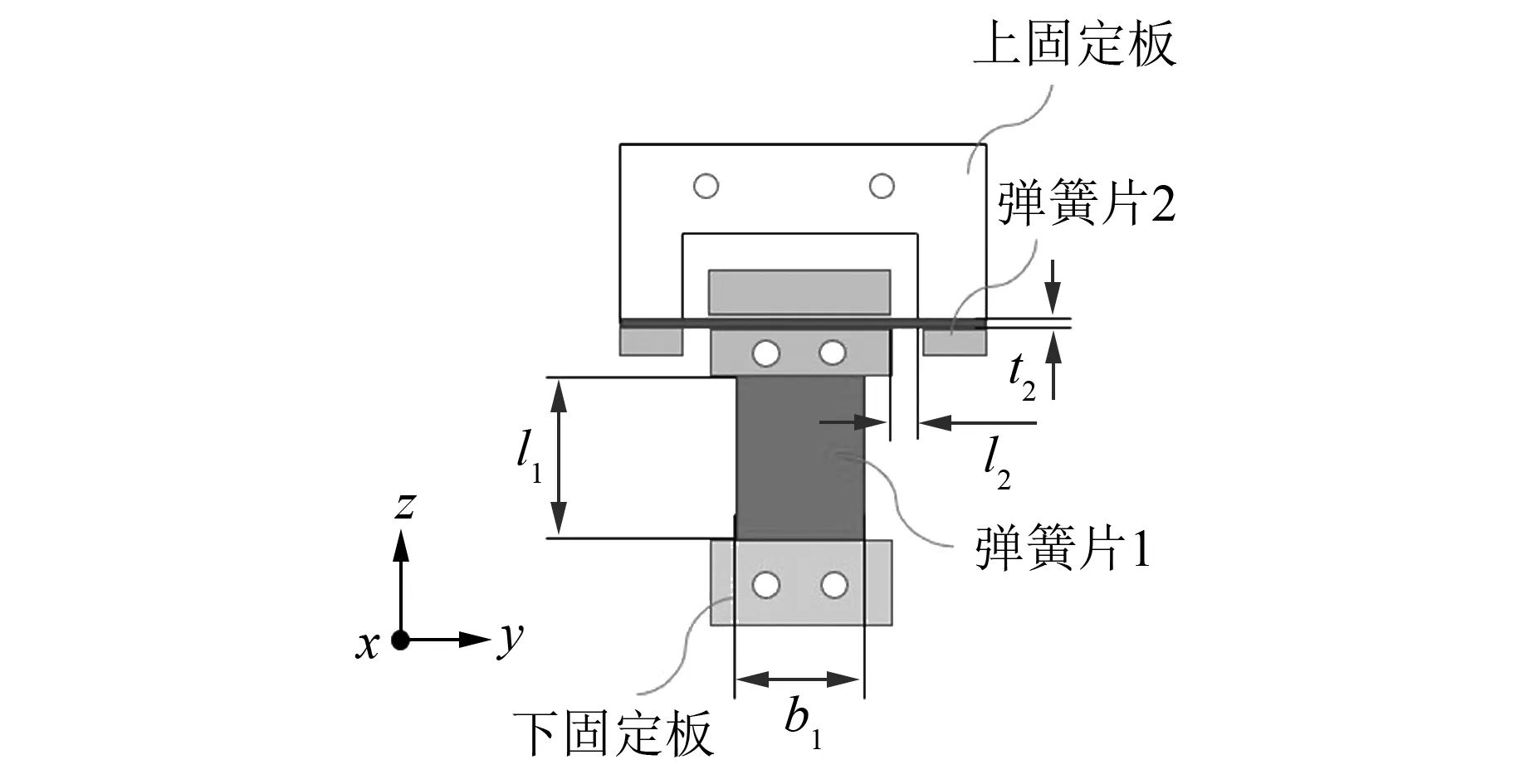
图10 挠性弹簧结构

对挠性弹簧进行受力分析，如图11所示，设弹簧高度-厚度比Lo/t大于5。在外力P作用下，挠性弹簧微小变形满足欧拉伯努利梁变形公式：

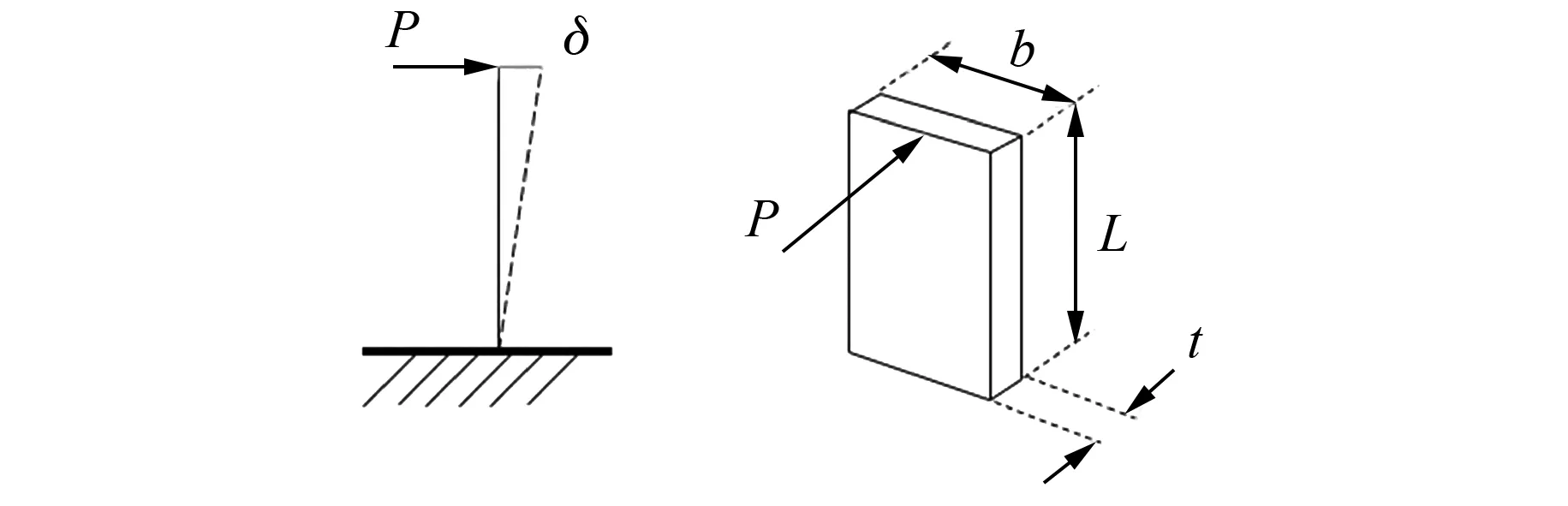
图11 挠性弹簧受力图

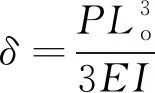
(17)

挠性弹簧截面矩：

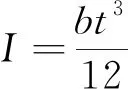
(18)

式中：b、t分别为挠性弹簧宽度和厚度。

由式(17)、式(18)得到弹簧刚度：

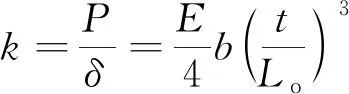
(19)

根据式(19)得到弹簧x轴刚度与z轴刚度：

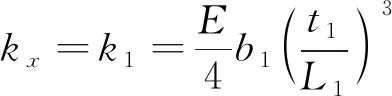
(20)

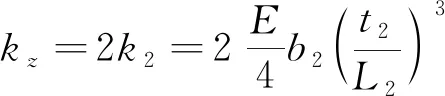
(21)

式中：b1、b2、t1、t2、L1、L2分别为弹簧片1、2的宽度厚度和高度。

表2为挠性弹簧的具体参数，代入表2的数据，得到kx=kz=1.09×105N/m。

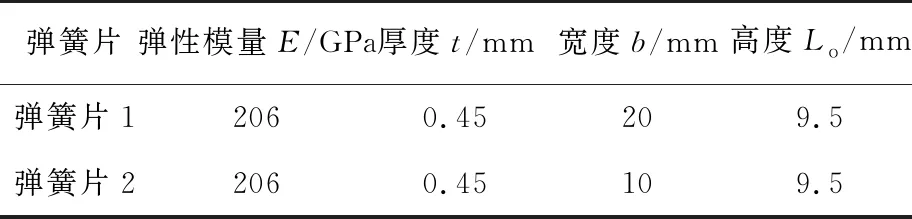
表2 挠性弹簧具体参数

4 微动台PD控制方法与仿真分析

4.1 PD控制系统设计

建立基于PD控制的位置闭环控制系统，如图12所示。其中，r、xout、H、Fr分别表示位置环输入、位置环输出、位置反馈信号和外部扰动力。ke、kE、Lc、Rc分别表示音圈电机力常数、反电动势常数、电感和电阻。kP、kD表示PD控制器的比例、微分参数。

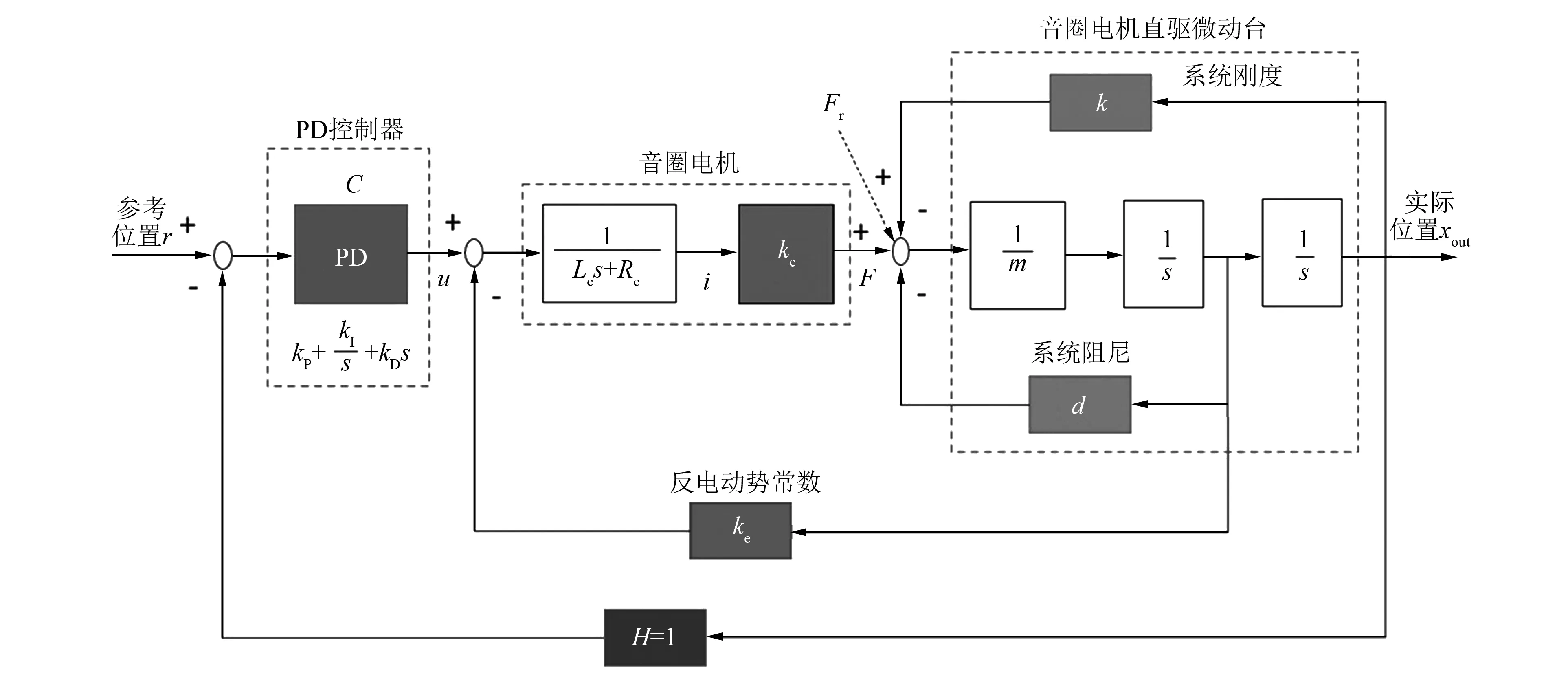
图12 微动台位置闭环控制框图

不考虑外扰力，则位置闭环传递函数为

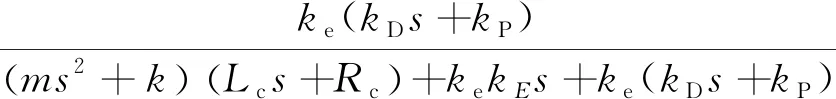
(22)

表1中音圈电机电感Lc=4.43 mH，可认为Lc趋近于0，传递函数变为

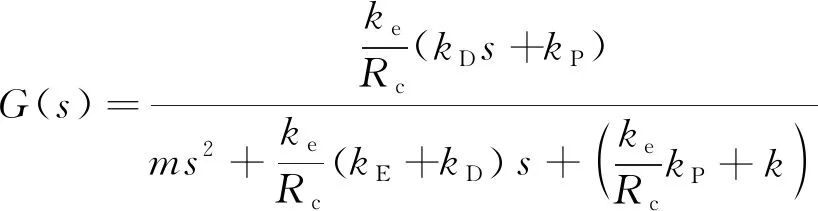
(23)

在式(24)、式(25)中，分别定义dv、kv，前者决定系统阻尼，后者决定系统刚度。

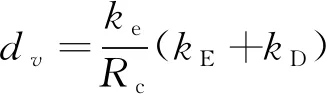
(24)

(25)

由式(23)可知，系统阻尼由音圈电机反电动势常数kE和PD微分常数kD决定，系统刚度取决于PD比例常数kP和弹簧刚度k。dv、kv分别为系统虚拟阻尼和虚拟刚度。

(26)

式中:ωn、ζ分别为系统固有频率和阻尼系数。

让系统达到最佳阻尼状态，取ζ=0.7，dv=4 340 N·s/m。代入式(24)，求得KD约为212。

式(25)中，因k值较大，kP可在1～8 000以内取值。

4.2 PD控制仿真与分析

微动台为开环控制，位移输出与音圈电机推力输入满足传递函数式(14)，系统固有频率由微动台质量和弹簧刚度决定。采用PD反馈控制，表3为微动台PD控制参数，测试1至测试4输入为参考位置阶跃。

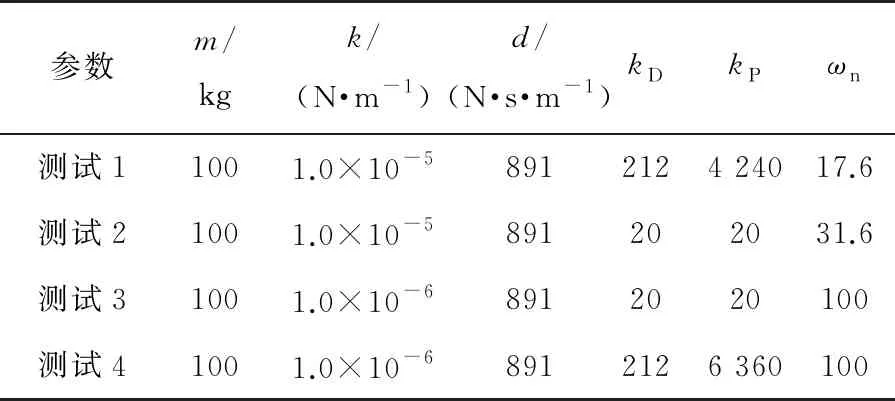
表3 微动台PD控制参数

图13为对应的响应输出曲线。在测试1中kD赋值212，以此保证系统达到最佳阻尼状态，kP取值为kD大小的20倍，使系统超调量约为28%，调节时间约为0.3 s。在测试2中，弹簧刚度保持不变，kD与kP赋值20，kD较小，系统处于欠阻尼状态，调节过程中会出现振荡，超调量过大。在测试3中，弹簧刚度增大，kD与kP仍赋值20，系统响应频率增大，但仍处于欠阻尼状态，调节过程中出现振荡，超调量过大。测试4中弹簧刚度保持不变，阻尼系数有所增加，系统调节时间约为0.3 s，但调节过程中超调量过大。通过试验对比，发现测试1中的参数可以使闭环反馈系统有较好的响应结果。

图13 不同测试条件下反馈对应位移阶跃输入的响应

5 结 语

基于音圈电机直驱的微动台系统，设计一种挠性弹簧，为系统提供外部刚度。挠性弹簧无需解耦即可实现x和z两个自由度精密运动。微动台采用PD位置闭环反馈伺服控制，仿真分析了系统在不同刚度、阻尼以及PD参数下的动态响应。仿真测试结果表明，微动台在参考位移阶跃输入下，超调量低于30%，在1 mm以内，调节时间小于0.3 s。系统能够实现喷墨打印的扫描主轴直线度误差补偿。