基于三维激光点云的零件表面缺陷检测
2022-08-30朱秀敏
朱秀敏,黄 磊
(南京林业大学机械电子工程学院自动化系,江苏南京 210037)
0 引言
贵重零件表面缺陷的修复在工业领域有着广泛的需求。随着3D打印技术的快速发展,如果能够获得零件表面缺陷的准确3D尺寸,可以利用金属3D打印技术对零件表面的缺损部位进行填补和修复,以提高零件的使用寿命。这一修补方法正在零件修复领域得到越来越多的应用。因此对零件表面缺陷3D尺寸的精确测量显得尤为重要。
目前工业上常用的零件缺陷检测方式主要包括:磁粉检测法、渗透检测法、涡流检测法、超声波检测法、X射线检测和机器视觉检测法等[1]。前3种方法容易受材料种类、零件形状限制,而X射线对人体有害,超声波检测不适合结构复杂的工件,机器视觉检测法难以提取出精确的零件缺陷3D尺寸。本文使用3D激光扫描仪采集缺陷零件的表面点云,与CATIA导出的完整零件点云作对比,通过滤波、SAC-IA粗配准、Huber损失函数优化的ICP精确配准、最邻近查找等操作提取出缺陷部位点云。实验结果表明:具有不受零件形状、缺陷形状限制,适用范围广、自动化检测、精度高等优点。
1 点云数据获取及预处理
1.1 3D扫描仪原理
本文使用PhoXi 3D扫描仪对受损零件进行测绘,得到其三维点云数据。扫描仪实物如图1所示。

图1 PhoXi 3D扫描仪示意图
PhoXi 3D激光扫描仪采用波长639 nm的红色可见光为光源,CMOS传感器成像,兼具3D激光测绘和2D CMOS相机功能,无需用户自己进行激光点云坐标系和相机坐标系的对齐,可直接输出物体的彩色点云。它的一帧输出点云可达320万个点,对应的分辨率达2 064像素×1 544像素,测距距离2 m,并可按照设置的最大测距误差门限(最小1 mm)输出所有符合这一要求的点[2-3]。生成的点云坐标系如图2所示,原点一般位于标记板右上角的第一个圆圈中。

图2 标记坐标系示意图
基于PhoXi 3D激光扫描仪的零件缺陷检测系统如图3所示,将零件置于标记板上,底部工作台旋转一圈,共扫描零件的8个不同的角度,形成8个点云文件。扫描仪采集到的数据包含零件点云的三维坐标、颜色等信息。

图3 基于PhoXi 3D激光扫描仪的零件缺陷检测系统
1.2 数据预处理
扫描仪将8个角度的点云数据生成8个点云文件,首先提取出这8个点云文件中的三维坐标,然后将这8个角度的点云合成零件点云。由于扫描仪在扫描零件时,会将标记板、工作台等物体一并扫入仪器中,因此还需要对采集的数据进行预处理以获得零件的点云,处理流程如图4所示。

图4 原始点云预处理流程图
统计滤波能将原始点云中稀疏的离群点剔除,如测量时产生的噪声、离零件较远且与零件无关的杂物等。统计滤波算法设想,假设一个含有离散点的点云,其滤除离散点后的点云中所有点到其各自邻域的平均距离服从高斯分布,由于离散点相对于主体点云是少量的,故可认为原始点云与滤除离散点后的点云的均值与标准差相同[4]。统计滤波的流程如下:
(1)对原始点云数据集P={p1,p2,…,pn}进行统计滤波,即对其中每一个点的邻域进行统计分析,计算点pi到最近的k个点的平均距离,记作Si,则由n个点的平均距离组成的点集S服从高斯分布。
(2)根据式(1)、式(2)分别计算点集S的均值μ、标准差σ。
(1)
(2)
(3)判断点pi与其邻域的平均距离是否在(μ-std·σ,μ+std·σ)范围内。如果在,则保留;如果不在,则作为离群点剔除。
算法中的k、std分别为邻域点的个数、标准差倍数,2个参数由人为设定,前者控制邻域大小,后者控制筛选的苛刻程度,适当的参数才能得到高质量的滤波结果[4]。
经过统计滤波后的点云仍有标记板、工作台2个不需要的平面数据,再进行RANSAC平面分割,则能够去除这2个平面。平面分割的步骤如下:
(1)从点云中随机抽取3个点,计算这3个点组成的平面表达式。
(2)计算其他所有点到该平面的距离,如果小于阈值d则认为是同一个平面的点,添加到该平面的点集中。
(3)如果同一个平面的点的个数超过N则保留这个平面并停止迭代,否则重复步骤(1)(2)(3),直到找到迭代次数达到阈值。最终可以得到一个完整平面的点集。
运用2次RANSAC地面分割后,标记板与工作台2个平面的点云均可被剔除。剩下的部位则为零件以及周围噪声的点云,最后采用半径滤波即可去除零件周围的噪声。算法思路如下:判断每一个点半径为r的邻域内的点的个数是否小于阈值,若小于,则认为该点为噪声点并去除,否则保留。
2 点云配准
点云配准的实质是寻找一个最优的变换矩阵,使得源点云经过该变换能够和目标点云的空间位置差别最小化。本文采用采样一致性初始配准(sample consensus initial alignment,SAC-IA)算法进行粗配准,Huber损失函数优化的迭代最近点算法(iterative closest Point,ICP)进行精确配准,配准流程如图5所示。

图5 缺陷点云配准流程图
首先对零件点云数据进行预处理,对缺陷点云和完整点云使用体素下采样来提高算法的效率;用SAC-IA算法迭代得到初始变换矩阵,实现初步配准;最后利用Huber损失函数优化的ICP算法迭代得到最优变换矩阵,实现精确配准。
2.1 点云粗配准
初值的选取对于ICP算法十分重要,如果没有合适的初值,会导致ICP配准出现局部最优的情况,很难迭代出全局最优变换矩阵[5]。因此,在进行精确配准之前,先进行粗配准。由于零件的形状、缺陷位置对于点云质心、主成分影响较大,速度更快的PCA粗配准算法对于零件表面缺陷检测不合适,因此本文采用SAC-IA算法,即采样一致性初始配准算法[6]。该算法依赖点特征直方图(point feature histograms,PFH),使用类似RANSAC算法的思路进行配准[7]。由于计算PFH的特征描述子速度较慢,考虑代码效率,首先需要对原数据进行降采样,再使用快速点云直方图(FPFH)特征描述子。
SAC-IA粗配准过程如下:
(1)分别计算缺陷点云P和完整点云Q的FPFH特征描述子的值。每次从缺陷点云中随机选取n(n≥3)个点作为一个子集Pi={p1,p2,…,pn},这n个点两两之间距离大于最小阈值[8]。
(2)在FPFH特征空间中进行最近邻查找,检测在Q中FPFH描述子相似的点,从相似点中随机选出1个点作为缺陷点云在完整点云中的对应点,这些相似的点组成对应点集Qi={q1,q2,…,qn}。
(3)通过奇异值矩阵分解法(SVD)求解Pi、Qi对应点之间的变换矩阵Ti,元素构成如式(3) 所示,通过求解对应点变换后的距离误差和来判断当前的配准效果[9]。如果不满足阈值要求,则重复步骤(2)(3),直到迭代出误差最小且满足阈值要求的变换矩阵。距离误差和函数常用Huber惩罚函数表示[10],Huber函数如式(4)所示:
(3)
(4)
la=‖qa-(Rpa-t)‖2
(5)
式中:Ti为点集Pi到Qi的变换矩阵;Ri、ti分别为变换矩阵中的旋转、平移矩阵;ml为预先给定值;la为第a组对应点变换之后的距离差;pa、qa分别为点集Pi、Qi中的点。
2.2 点云精确配准
经过粗配准后的2组点云已经大致重合,但仍存在偏差,为了更好地提取缺陷部位,还需要进一步精确配准。传统的ICP算法以源点云与目标点云对应点之间的距离作为配准结果的评估准则,容易受错误的对应点以及噪声的干扰,导致配准精度降低[11]。由于缺陷点云的缺陷部位对于完整点云来说相当于是外点,并且由扫描仪得到的数据有噪声干扰,于是本文并不采用传统点到点的ICP。而点到面的ICP相对于点到点的ICP能更好的对错误的对应点、噪声鲁棒,且迭代收敛速度更快[12]。故这里采用点到面的ICP,建立kd-tree加速最邻近查找,并使用Huber损失函数优化,以提高配准的鲁棒性[13-14]。
ICP算法包含离群点去除阶段与误差最小化阶段,2个阶段可以概括为通过最小化目标函数式(6)来估计转换矩阵T[15]。
(6)
式中:ρ(·)为成本函数;pi、qj分别为缺陷点云P以及完整点云Q中的点;nj为qj的法向量;T为变换矩阵。
为了简化式(6)中的双重求和,通常采用对应点的子集来近似,这里使用每个pi的最邻近点来近似。将成本函数ρ(·)分解为权重ω和平方误差项来迭代求解最优变换矩阵T[16-17]。每次迭代都会将先前的变换分配给最后估计的变换,直到收敛。式(6)简化后为:
(7)
Lm(T)=min‖(Tpm-qm)·nm‖2
(8)

基于Huber损失函数优化的ICP本质是对式(7)中的ω函数的改进,式(9)即为Huber对ω的实现[18]。
(9)
式中k为设定的超参数。
算法大致思路如下:
(1)令粗配准后的转换矩阵为初始矩阵。
(2)缺陷点云经过变换矩阵旋转平移形成新的点云。
(3)建立kd-tree,通过最邻近查找找出新的点云子集在完整点云中的对应点子集,再根据式(7)~式(9)去除离群点并计算出新的点云与完整点云之间的最优变换矩阵T以及2组点云之间的最小误差Lm(T)。
(4)判断误差是否小于阈值,如果是则保留配准后的点云,否则重复步骤(2)、(3),直到迭代出符合要求的最优变换矩阵。
3 缺陷部位提取
缺陷点云与完整点云配准后,可进一步提取缺陷部位,流程如图6所示。考虑到点集中可能仍然有噪声,于是在最后加入统计滤波器,以提取出完整的缺陷部位。

图6 缺陷部位提取流程图
4 实验结果
为了验证本文算法对于零件缺陷检测的合理性,使用Python语言和开源点云工具库Open3D 0.13.0编写算法进行试验。算法运行平台为CPU频率2.8 GHz,内存8 GB,运行Win10的计算机。为了验证算法的可行性,本次实验运用了2组零件点云数据,缺陷零件的数据为真实测量数据,完整零件的数据为CAD模型导出数据,其中缺陷的部位分别为破洞、凹陷,此次实验中分别命名为零件1、零件2。
首先是数据的预处理,以零件1为例,PhoXi 3D扫描仪采集原始数据为零件8个角度的点云数据,这8个角度去重、融合后的点云合成如图7(a)所示。经过统计滤波、2次RANSAC地面分割和半径滤波后提取出完整零件点云过程如图7(b)~图7(d)所示。

图7 数据预处理结果
由表1可知,待检测的原零件点云规模较大,影响配准效率。故需要对原点云进行降采样,这里采用体素下采样。使用降采样后的数据进行全局配准,再使用原数据进行精确配准,以获得契合点云,为下一步缺陷部位提取做准备。
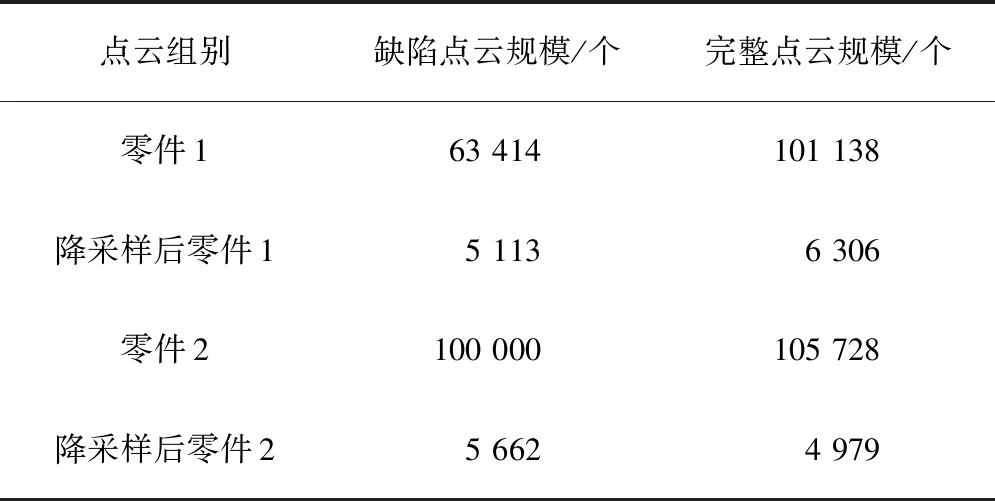
表1 缺陷点云和完整点云规模统计
表2中的配准误差采用均方根误差(root mean sq-uare error,RMSE),从表2可知:SAC-IA速度虽然不如PCA,但误差远小于PCA。故本文采用SAC-IA+改进的ICP算法来配准,配准结果如图8所示,深色的为缺陷零件点云,浅色的为完整零件点云。可以看出,经过粗配准后,2个点云已大致重合;再经过精确配准,2个点云完全重合。

表2 零件1的各配准算法结果比较
采用kd-tree加速的最邻近查找提取缺陷部位点云如图9所示,可以看出该算法能够较好的提取零件表面缺陷部位的3D点云,并且通过该数据,可以进一步对零件做出3D打印修复。

图9 缺陷部位提取结果
5 结束语
本文提出了一种用于零件表面缺陷部位定位与测量的方法。使用3D扫描仪得到零件表面点云,先通过预处理,与CATIA生成的完整零件点云进行SAC-IA粗配准和Huber损失函数优化的ICP精配准,然后进行最邻近查找,最后成功提取缺陷部位的精确点云。点云中包含缺陷部位的形状、具体尺寸,能够以此进行在线的3D打印修复。实验表明:本文的检测算法速度快、精度高。
