含GTO的新型静止无功发生器拓扑的动态模型建模方法
2022-08-30朱亮亮张永熙于一三柯振宇杨胜林
朱亮亮,张永熙,于一三,柯振宇,杨胜林
(国网新疆电力有限公司乌鲁木齐供电公司,新疆 乌鲁木齐 830000)
0 引言
随着电力电子技术的应用越来越广泛,电能质量问题日趋繁多[1]。在无功补偿领域,静止无功发生器并联在电网母线上,可对系统双向输出无功,且输出的无功电流连续可调,具有响应速度快,谐波特性好等优点[2]。静止无功发生器的使用,可以有效解决电力系统无功问题,为系统电压提供支撑,有利于提升系统稳定性,在电力系统与工业界受到普遍重视。
国内目前在中高压无功补偿的场景中,级联H桥结构应用较多,但仍存在一些问题亟待解决,由于大量使用功率开关器件,级联H 桥结构的静止无功发生器成本偏高,且控制复杂[2-5]。
文献[6]对柔性直流输电系统进行分析,通过对柔性直流输电系统的基本结构和工作原理进行介绍,利用MATLAB 和Simlink 软件将各模块进行模型建立,搭建柔性直流输电系统及其控制器的仿真模型建立,并在该模型的基础上进行稳态仿真模型及暂态故障的仿真,通过仿真验证了所提方案的有效性,该工作的基础即是数学模型的建立。
文献[7]介绍了单相全桥逆变电路,提出了一种大信号模型快速建模方法,通过理论计算就能够获得换路设计的大信号模型。所得模型可以用于控制器参数设计;该文献采用的脉宽调制开关函数模型大体上保留了原始电路结构,可以详细观察内部各电路部分的端口电压等特征量,但该方法更偏向于多变换器组合的系统级仿真,对具体电路的设计不能起到指导作用。
文献[8]利用导纳模型建立了LCL 型并网逆变器的小信号模型,该方法主要利用派克变换寻找双dq坐标系之间的关系,一定程度上解决锁相环(Phase Locked Loop,PLL)对LCL 型并网逆变器建模的影响,该方法还进一步研究了逆变器的输出导纳特性,分析了PLL 和LCL 滤波器参数在dq坐标系下对系统稳定性的影响。
小信号建模是目前对电网稳定性分析和变流器控制器设计的主要方法,根据滤波器和线路的动态特性又可以将小信号模型分为高阶和低阶模型,文献[9]则利用逆变器并网系统建立了高阶小信号模型,并利用稳态方程对滤波器的动态特性进行表述,通过MATLAB 软件对所提模型的正确性进行了验证,最后利用两种不同的方法,得出了降阶模型与误差表达式的关系,但该方法并不能得到中高频特征根,在低阻抗比或感性网络中存在稳定性判断错误的可能性。
在分布式电源大规模接入配网的背景下,由于详细模型需要考虑电力电子器件的非线性因素,步长需要设计的非常小,仿真的速度很慢,反之,若忽略非线性因素,则会导致模型不能反映系统整体的特性和影响,文献[10]提出一种正负序分离控制的方法,在该方案的基础上,对分布式电源进行细致分析,采用动态相量建模,最终分别在PSCAD 和MATLAB 上建立暂态模型,验证了所提方案的有效性。
在电力电子器件损耗方面,现有方案很多依靠器件厂家提供的数据手册,而厂家所采集的数据并不是实际工况所取得的,文献[11]提出一种IGBT 离线测试平台,该平台可对逆变电路在各种模型下进行在线建模,能够模拟复杂工况下的杂散参数,并利用该平台得到多维数据库下逆变器实际工作的开关能量损耗,通过计算得出逆变器的实际损耗,经对比验证了该建模方法的正确性,为逆变器结构优化设计提供了参考方案。
针对上述存在的问题,对H 桥结构与半桥结构进行分析,认为可以对半桥电路进行进一步改进,降低开关器件的使用数量,并提出一种含门极可关断晶闸管(Gate Turn-off Thyristor,GTO)的静止无功发生器拓扑,为验证所提方案的有效性。从建立数学模型的角度进行分析,首先对单相单子模块进行分析,搭建受控源等效电路,并在此基础上建立小信号模型;然后总结单相单子模块的建模方法,并应用至子模块级联的系统建模中;最后通过仿真,验证输出电压扰动与占空比扰动之间的关系。
1 新型静止无功发生器基本结构
经过对传统半桥电路进行分析,认为可通过去除T2 元件,用来降低静止无功发生器的开关器件数量,将T2 去除后,电路可通过开关管控制电容充放电实现DC/DC变换,如图1所示。
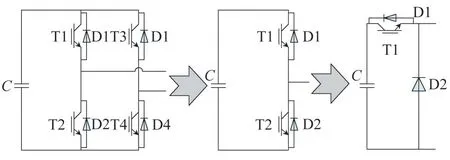
图1 电路子模块的演进
将子模块级联,放置在整流H 桥后,所提新型静止无功发生器拓扑如图2 所示,可通过H 桥实现DC/AC 变换,且通过子模块级联可增加电压电平数,使电压谐波含量更少,由于级联常用在高压场景中,对H 桥电路的耐压水平要求较高,对其开关频率要求较低,此处的H桥器件选用GTO。
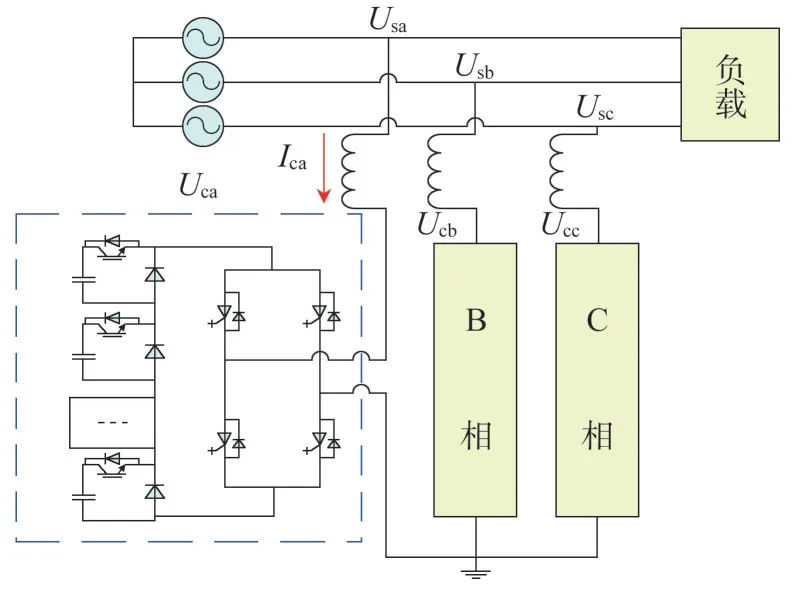
图2 新型级联静止无功发生器的拓扑结构
2 新型静止无功发生器动态模型
2.1 单相单模块动态模型
H 桥电路的变流过程十分成熟,此处不再分析,图3 和图4 为单相改进半桥子模块变换器的等效主电路,分别从电容充电和放电两个角度来分析,只考虑正常工作模式。
2.1.1 电容放电工作模式
电容放电工作模式[12-14]等效电路如图3所示。
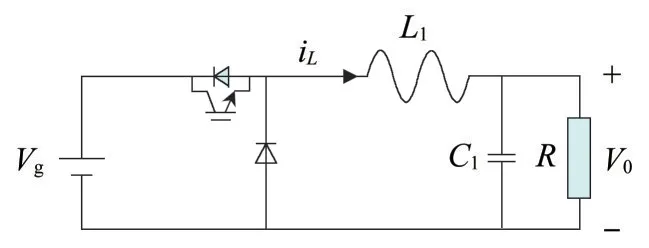
图3 电容放电工作模式
图3 中,Vg为直流侧输出电压,此处使用直流电源等效,L1、C1、R为输出负载;iL为电感电流,输出端C1与R并联,再与L1串联,Vo为输出电压,开关管的周期为TS,开关管导通时间为ton,关断时间为toff,且ton+toff=TS。
开关管导通时,其电路如图4 所示,其状态方程如式(1)所示。
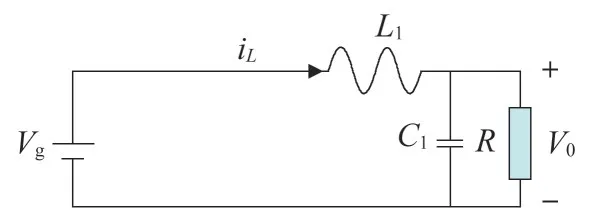
图4 开关管导通时等效电路
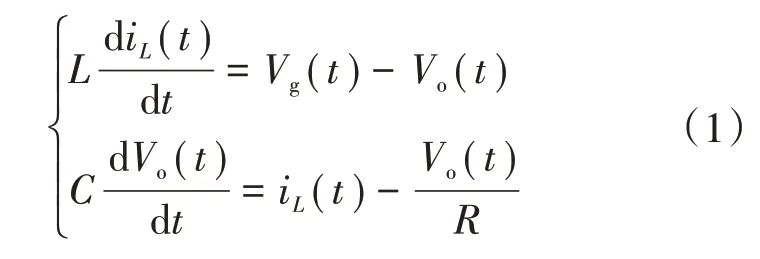
当开关管断开时,忽略二极管压降,其等效电路如图5所示,则状态方程如式(2)所示。
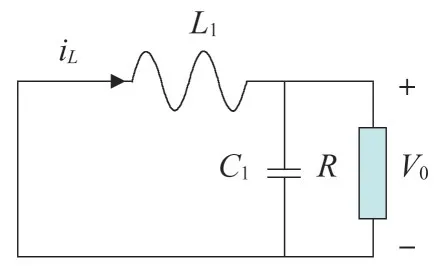
图5 开关管断开等效电路
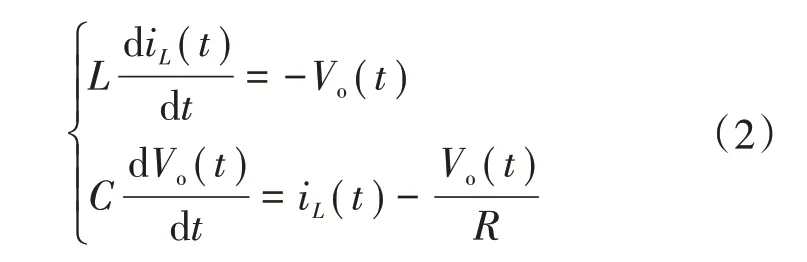
因为开关函数不连续,须对式(1)—式(2)求开关周期平均,得
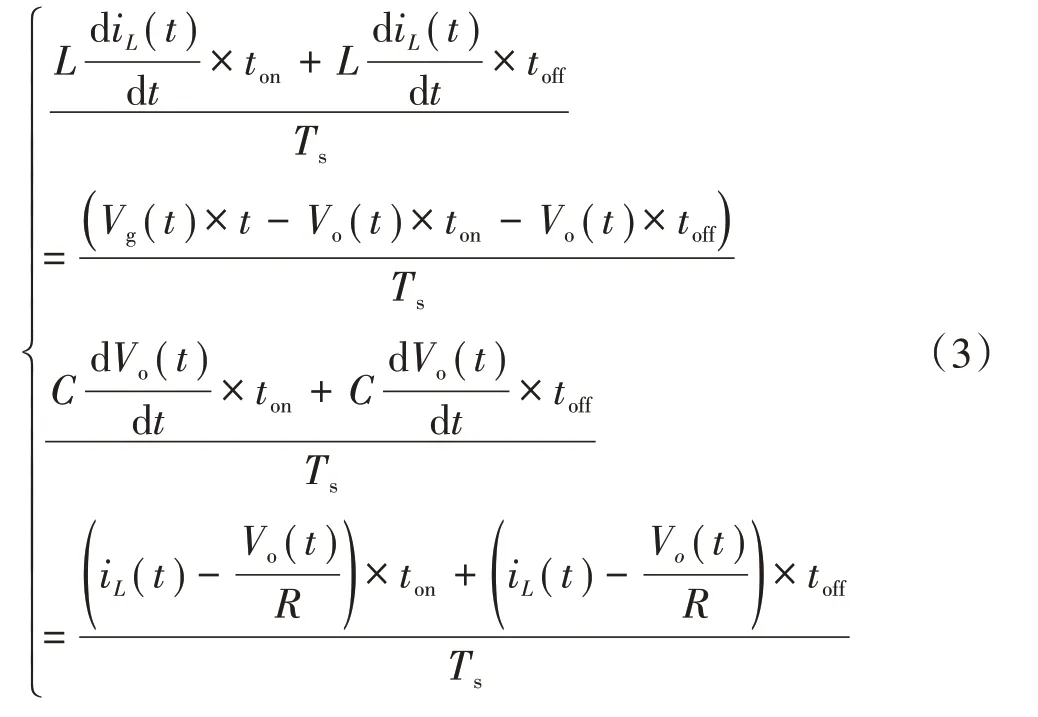
定义开关信号占空比为D,对式(3)简化后可得
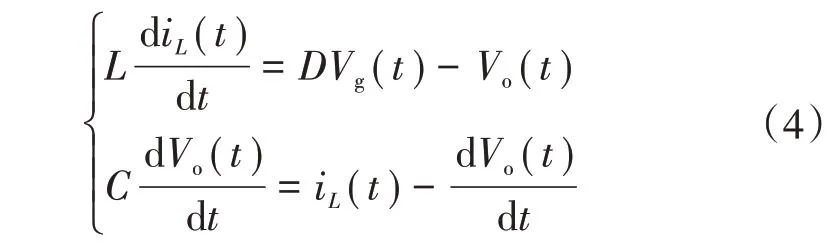
式(4)为电容放电模式在一个开关周期的状态方程,也是其静态工作点的方程,其受控源形式的等效电路模型如图6所示。
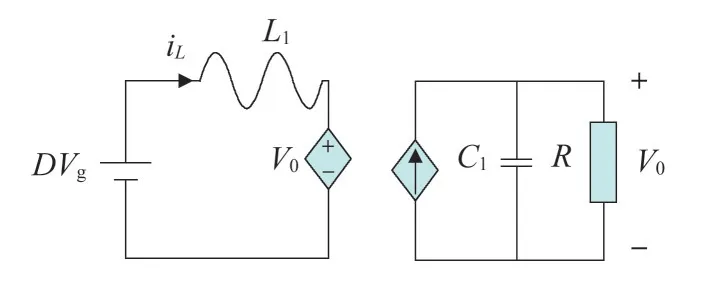
图6 单相子模块等效电路模型
2.1.2 电容充电工作模式
电容充电工作模式的等效电路如图7 所示,图7中,Vd为电容电压,L2为交流侧输出输出端电感,Rd表示模块等效损耗部分与电容并联,输入电压用
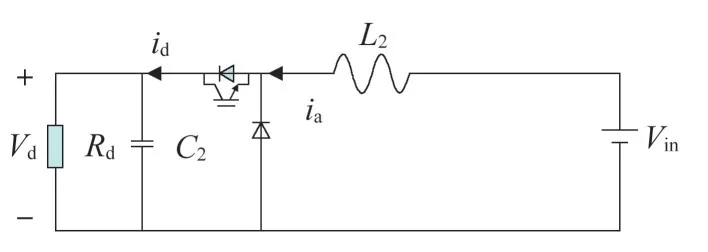
图7 电容充电放电模式
直流源Uin等效。
电容充电工作模式下,开关管占空比对电路的无影响,且ia=id,其动状态方程如式(5)所示。
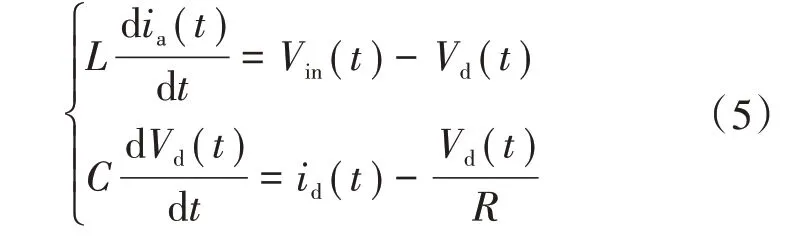
其受控源等效电路如图8所示。
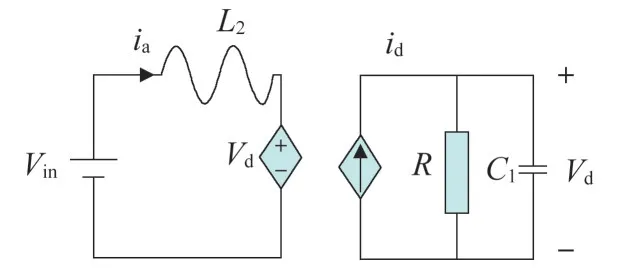
图8 电容充电模式等效模型
因电容充电模式下开关管对电路无影响,因此后续分析过程将不再对其进行讨论分析。
2.2 电容放电小信号模型
为建立小信号模型[15-18],令
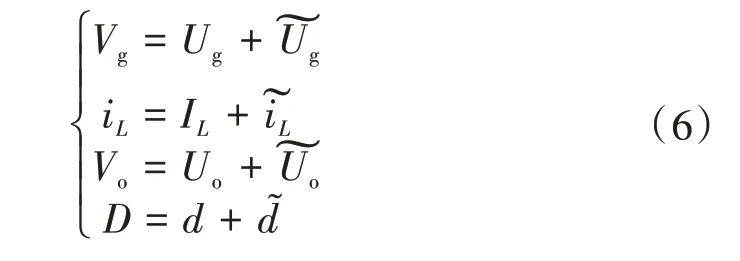
式中:Vg为直流侧输入电压;Ug为直流侧输入电压的静态工作点;iL为输出电流;IL为输出电流的静态工作点;Vo为输出电压;Uo为输出电压的静态工作点;D为占空比;d为占空比的静态工作点为扰动量。
将式(6)代入式(4),得
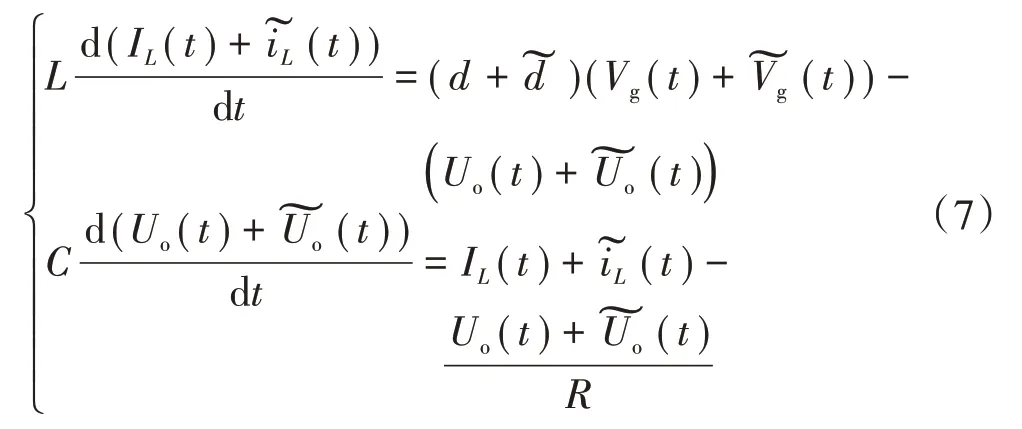
忽略高次项,考虑静态工作点,则可得到单相单模块小信号模型为
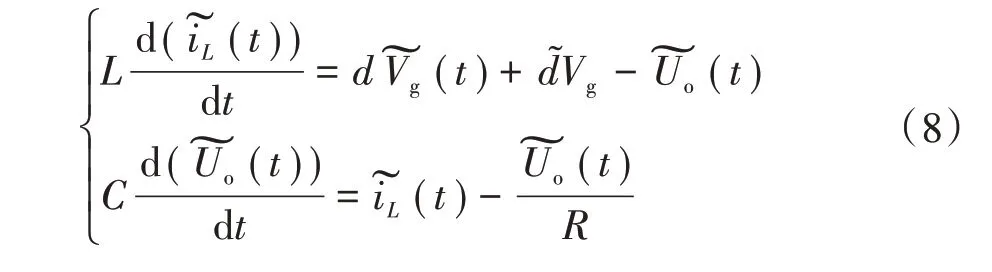
受控源形式的电路模型如图9所示。
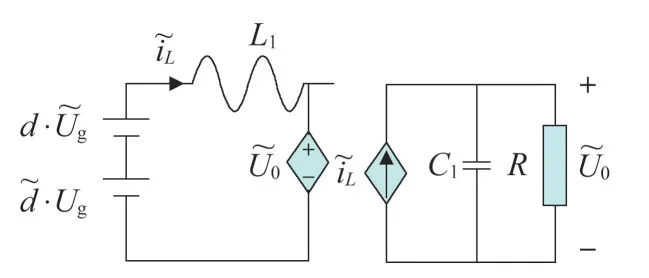
图9 单模块受控源等效模型
2.3 单相级联改进半桥的动态模型
设单相N个子模块的新型静止无功发生器拓扑如图10 所示,图中Vg为直流侧输入电压,iL为输出电流,Vo为输出电压,L是交流侧输出端电感,输出端R、C并联。
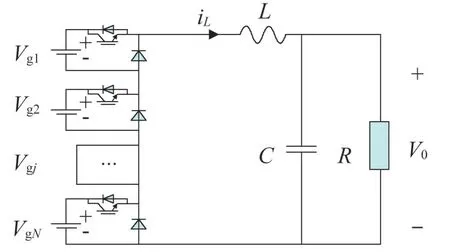
图10 子模块级联等效电路图
参考前文推导过程与方法,可得到级联改进半桥子模块的状态方程如式(9)所示。
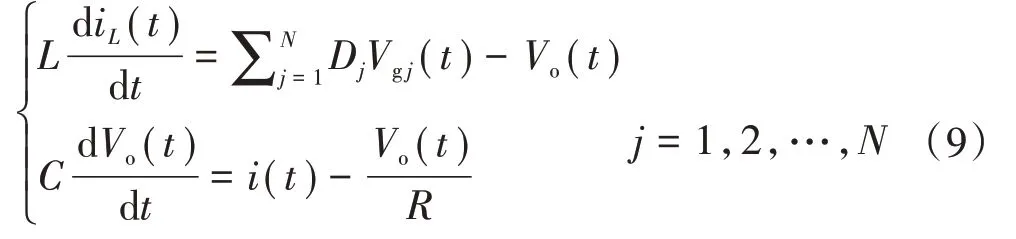
式中:Dj和Vgj(t)分别为第j个子模块的占空比和直流侧电压,其受控源等效电路如图11所示。
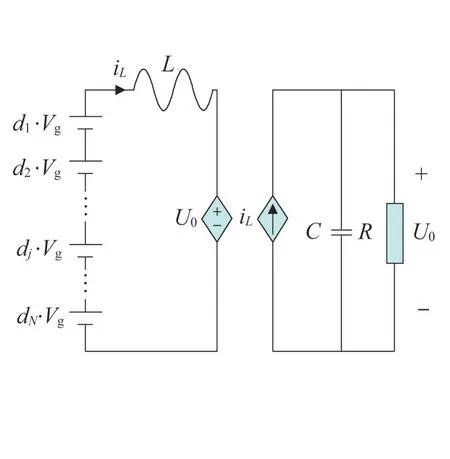
图11 子模块级联受控源等效电路
同理可得,在单相单子模块小信号模型的基础上,单相级联改进半桥型静止无功发生器的小信号模型如式(10)所示。
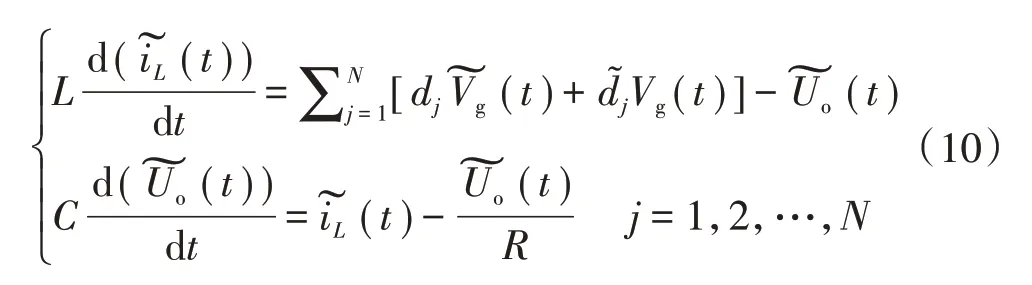
受控源形式及传递函数方块图形式的电路模型如图12所示。
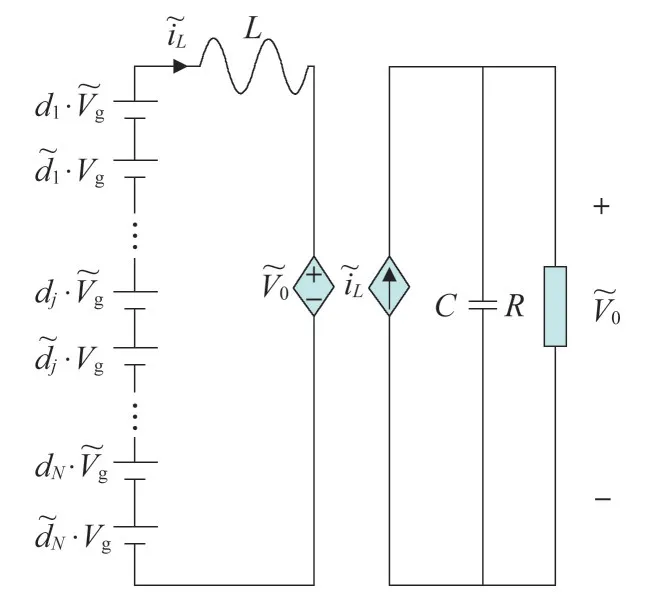
图12 子模块级联小信号等效电路
3 仿真验证
对新型静止无功发生器进行动态建模,可对装置级控制策略的起到一定帮助,使用Simulink 软件对上述模型进行仿真验证,主要是针对原始电路与其小信号模型的频率响应曲线进行仿真结果对比,表1为新型静止无功发生器参数。
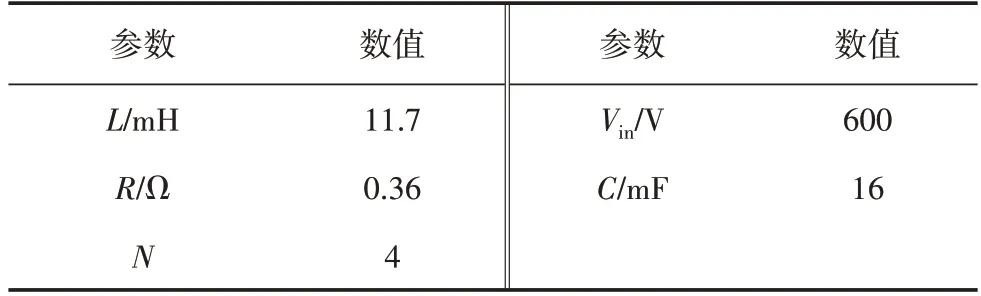
表1 新型静止无功发生器参数
在小信号建模的过程中,系统的传递函数与静态工作点有关,此处D分别选取0.4 和0.9 两种情况下计算静态工作点,并进行仿真,此处对输出电压Vo和占空比D之间的频率特性曲线进行仿真。
仿真采用等效原则,单相单子模块的仿真,输出端电感为11.7 mH,电阻0.36 Ω,电容16 mF,载波频率12 kHz,图13 和14 给出了单相单子模块在静态工作点0.4 和0.9 时的输出电压Vo和占空比D之间的频率特性曲线,在低于开关频率的低频段,原电路与小信号模型的频率特性基本重合,当频率高于开关频率时两者出现偏差,验证了小信号模型的合理性。
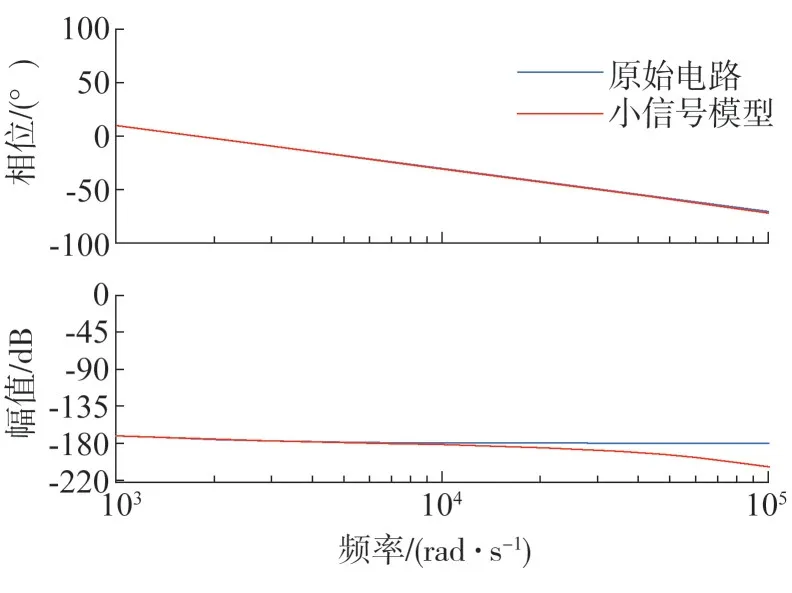
图13 单相单模块频率响应(D=0.4)
子模块级联采用4 模块级联等效,采用载波层叠调制,图14和15为单相子模块级联在静态工作点0.4 和0.9 时输出电压Vo与占空比D之间的频率特性曲线。在仿真中,Vgj=Vg,Dj=d,j=1,2,…,N。从图中可以看出,原电路与小信号模型的频率特性基本重合,只在高于开关频率时,二者出现差别,这也证明了所建立子模块级联结构小信号模型的有效性。
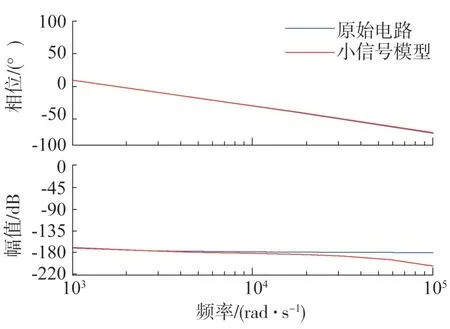
图14 单相单模块频率响应(D=0.9)
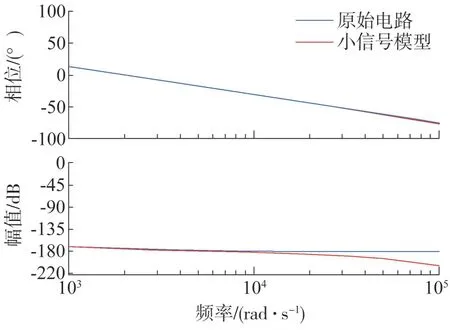
图15 子模块级联频率响应(D=0.4)
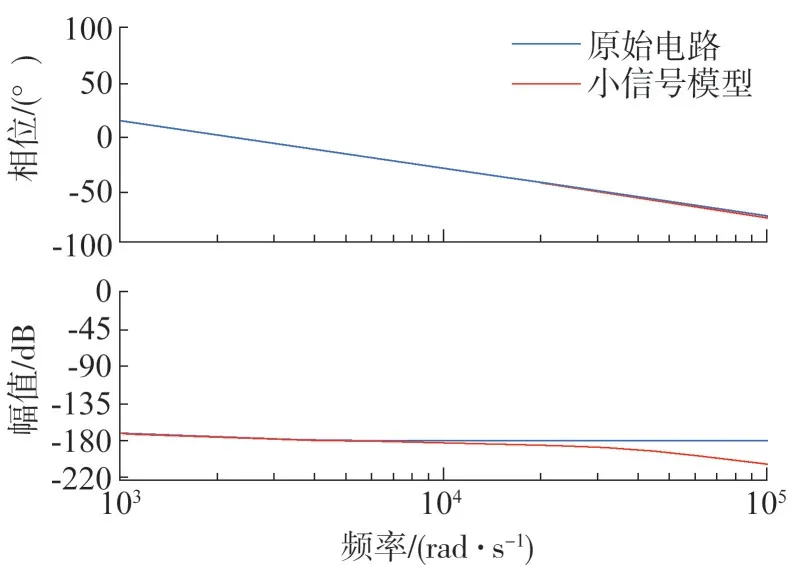
图16 子模块级联频率响应(D=0.9)
4 结语
提出一种含GTO 的新型静止无功发生器,并建立单相单子模块级联的等效模型与小信号模型,并在此基础上建立了子模块级联的等效模型与小信号模型,经仿真验证了所提模型的合理性,模型的建立为装置级控制策略的探索奠定了基础,为日后新型静止无功发生器的数学模型建立提供了一条新的思路。
